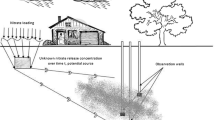
Abstract
Contaminant source identification in groundwater system is critical for remediation strategy implementation, including gathering further samples and analysis, as well as implementing and evaluating different remediation plans. Such problem is usually solved with the aid of groundwater modeling with lots of uncertainty, e.g. existing uncertainty in hydraulic conductivity, measurement variance and the model structure error. Monte Carlo simulation of flow model allows the input uncertainty onto the model predictions of concentration measurements at monitoring sites. Bayesian approach provides the advantage to update estimation. This paper presents an application of a dynamic framework coupling with a three dimensional groundwater modeling scheme in contamination source identification of groundwater. Markov Chain Monte Carlo (MCMC) is being applied to infer the possible location and magnitude of contamination source. Uncertainty existing in heterogonous hydraulic conductivity field is explicitly considered in evaluating the likelihood function. Unlike other inverse-problem approaches to provide single but maybe untrue solution, the MCMC algorithm provides probability distributions over estimated parameters. Results from this algorithm offer a probabilistic inference of the location and concentration of released contamination. The convergence analysis of MCMC reveals the effectiveness of the proposed algorithm. Further investigation to extend this study is also discussed.






Similar content being viewed by others
References
Atmadja J, Bagtzoglou AC (2001) Pollution source identification in heterogeneous porous media. Water Resour Res. doi:10.1029/2001WR000223
Bauer S, Bayer-Raich M, Holder T, Kolesar C, Muller C, Ptak T (2004) Quantification of groundwater contamination in an urban area using integral pumping tests. J Contam Hydrol 75:183–213. doi:10.1016/j.jconhyd.2004.06.002
Bear J (1979) Hydraulics of groundwater. McGraw-Hill, New York
Carlin BP, Louis TA (2009) Bayesian methods for data analysis. CRC Press, Boca Raton
Cowles MK, Carlin PB (1996) Markov Chain Monte Carlo convergence diagnostics: a comparative review. J Am Stat Assoc 91:883–904
Duffy C, Brandes D (2001) Dimension reduction and source identification for multispecies groundwater contamination. J Contam Hydrol 48:151–165. doi:10.1016/S0169-7722(00)00169-8
Gelfand AE, Smith AFM (1990) Sampling-based approaches to calculating marginal densities. J Am Stat Assoc 85:398–409
Gelman A, Carlin JB, Stern HS, Rubin DS (1995) Bayesian data analysis. Chapman & Hall, London
Gilks WR, Richardson S, Spiegelhalter DJ (1996) Introducing Markov Chain Monte Carlo. In: Gilks WR, Richardson S, Spiegelhalter DJ (eds) Markov Chain Monte Carlo in practice. Chapman & Hall, London
Guo S, Yang R, Zhang H, Weng W, Fan W (2009) Source identification for unsteady atmospheric dispersion of hazardous materials using MCMC method. Int J Heat Mass Transf 52:3955–3962
Hassan AE, Bekhit MH, Chapman JB (2009) Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model. Environ Model Softw 24:749–763
Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57:97–109
Hazart A, Giovannelli JF, Dubost S, Chatellier L (2007) Contaminant source estimation in a two-layers porous environment using a Bayesian approach. In: IEEE international geoscience and remote sensing symposium
Huang CL, Hu B, Li X, Ye M (2011) Using data assimilation method to calibrate a heterogeneous conductivity field and improve solute transport prediction with an unknown contamination source. Stoch Env Res Risk Assess 23(8):1155–1167
Jin X, Mahinthakumar G, Zechman E, Ranjithan RS (2009) A genetic algorithm-based procedure for 3D source identification at the Borden emplacement site. J Hydroinfo 11(1):51–64
Joseph AS, Adams JB, McCabe B (2010) Methodology for Bayesian belief network development to facilitate compliance with water quality regulations. J Infrastruct Syst 16(1):58–65
Li Z, Mao X (2011) Global multiquadric collocation method for groundwater contaminant source identification. Environ Model Softw. doi:10.1016/j.envsoft.2011.07.010
Liu X, Cardiff MA, Kitanidis PK (2010) Parameter estimation in nonlinear environmental problems. Stoch Environ Res Risk Assess 24:1003–1022
Mahinthakumar G (1999) PGREM3D: massively parallel codes for groundwater flow and transport online manual. Available at http://www4.ncsu.edu/~gmkumar/pgrem3d.pdf. Accessed 10 Dec 2011
Mirghani BY, Mahinthakumar KG, Tryby ME, Ranjithan RS, Zechman EM (2009) A parallel evolutionary strategy based simulation–optimization approach for solving groundwater source identification problems. Adv Water Resour 32(9):1373–1385
Olmez I, Beal JW, Villaume JF (1994) A new approach to understanding multiple-source groundwater contamination: factor analysis and chemical mass balance. Water Res. doi:10.1016/0043-1354(94)90195-3
Rivette MO, Feenstra S, Cherry JA (2001) A controlled field experiment on groundwater contaminant by a multicomponent DNAPL: creation of the emplaced—source and overview of dissolved plume development. J Contam Hydrol 49:111–149
Sun NZ (1994) Inverse problems in groundwater modelling. Kluwer Academics, Norwell
Tompson AFB, Aboudu R, Gelhar LW (1989) Implementation of the three-dimensional turning bands random field generator. Water Resour Res 25(10):2227–2243
Wang H, Harrison KW (in press) Bayesian update method for contaminant source characterization in water distribution systems. J Water Resour Plan Manag. doi:10.1061/(ASCE)WR.1943-5452.0000221
Zheng C, Wang PP (1999) MT3DMS: a modular three-dimensional multispecies transport model for simulation of advection, dispersion, and chemical reactions of contaminants in groundwater systems; documentation and user’s guide
Acknowledgments
The authors thank the associate editor and anonymous reviewer for their insightful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, H., Jin, X. Characterization of groundwater contaminant source using Bayesian method. Stoch Environ Res Risk Assess 27, 867–876 (2013). https://doi.org/10.1007/s00477-012-0622-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-012-0622-9