Abstract
This is the first part of a two-part article on a hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress. We present the derivation of the new model, with focus on the mechanics of the out-of-plane deformation. Accounting for the out-of-plane normal stress distribution in the out-of-plane direction affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the shell. The improvement is beyond what we get from accounting for the out-of-plane deformation mapping. By accounting for the out-of-plane normal stress, the traction acting on the shell can be specified on the upper and lower surfaces separately. With that, the new model is free from the “midsurface” location in terms of specifying the traction. We also present derivations related to the variation of the kinetic energy and the form of specifying the traction and moment acting on the upper and lower surfaces and along the edges. We present test computations for unidirectional plate bending, plate saddle deformation, and pressurized cylindrical and spherical shells. We use the neo-Hookean and Fung’s material models, for the compressible- and incompressible-material cases, and with the out-of-plane normal stress and without, which is the plane-stress case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A shell formulation based on the Kirchhoff–Love shell theory and isogeometric discretization was introduced in [1,2,3]. It has the advantage of not requiring rotational degrees of freedom. Extension to general hyperelastic material can be found in [4, 5]. The formulation has been successfully used in computation of a good number of challenging problems, including wind-turbine fluid–structure interaction (FSI) [3, 6,7,8,9,10], bioinspired flapping-wing aerodynamics [11], bioprosthetic heart valves [12,13,14,15,16], fatigue and damage [17,18,19,20,21,22], and design [23, 24].
We are introducing a hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress. In the first part of a two-part article, we present the derivation of the model, with focus on the mechanics of the out-of-plane deformation. To determine the out-of-plane stress, we solve the linear-momentum-balance equation in the out-of-plane direction. Accounting for the out-of-plane normal stress distribution in the out-of-plane direction affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the shell. The improvement is beyond what was achieved with the new model’s precursor [5] by accounting for the out-of-plane deformation mapping.
A good number of shell models were presented earlier in the finite element context (see, for example, [25,26,27,28,29,30,31]), with significant effort in bending representation. The model in [28] is based on a mixed formulation. The model in [31] is based on a discontinuous-Galerkin type approximation to weakly enforce \(C^1\) continuity. The model in [30] is a TUBA family element, which has displacement derivatives as unknowns to attain \(C^1\) continuity in the displacement. The model we are introducing here is similar to the model in [25], which uses only one parameter to represent the out-of-plane deformation. Most of the other shell formulations, including some based on the Reissner–Mindlin theory, use the plane-stress assumption. The models in [26, 27], based on the Reissner–Mindlin theory, are, however, without the plane-stress assumption, in the finite element context.
Continuing what was started with its precursor, the model introduced here is extending the range of applicability of the Kirchhoff–Love shell theory to the situations where the Kirchhoff–Love shell kinematics is still valid yet the thickness or the curvature change is significant enough to make a difference in the response. Fung’s material model has different versions. In the version used in [13], the first invariant of the Cauchy–Green deformation tensor appears in a squared form. In the version used in this article, as in [5], it appears without being squared, and this version has been used in a number of arterial FSI computations [32,33,34,35,36,37,38,39] with the continuum model.
By accounting for the out-of-plane normal stress, the traction acting on the shell can be specified on the upper and lower surfaces separately. This enables not only more accuracy in the linear-momentum balance in the out-of-plane direction, but also representation of the moment the shear tractions on the upper and lower surfaces generate around the midsurface. With separate out-of-plane tractions on the upper and lower surfaces, for example, we can accurately model cases that might have nonzero net force even when those out-of-plane tractions have equal magnitudes and opposite directions. The net force would be nonzero because the upper and lower surfaces would have different areas due to the curvature. To accurately account for the moment generated by the separate shear tractions on the upper and lower surfaces, we improve the rotational kinematics in the model.
We note that accounting for the out-of-plane stress improves the out-of-plane deformation mapping also in cases with no traction on the upper or lower surfaces and no body force. Those would be the cases when the shell deformation is driven by the displacements and slopes specified along the edges of the shell.
We also would like to note that the level of accuracy we are striving for in representing the tractions on the upper and lower surfaces would be meaningful in an FSI computation only if the flow solution method can deliver those tractions with a comparable level of accuracy. That level of flow solution accuracy, especially in representing the shear stress, requires moving-mesh methods [9], where the high mesh resolution near solid surfaces follows the fluid–solid interface as it moves. That is now possible even in flow computations with actual contact between solid surfaces or some other topology change. The Space–Time Topology Change method [40] enabled that. We can both represent the actual contact and have high-fidelity, moving-mesh flow solution near the solid surfaces.
Our test computations are based on solving the linear-momentum-balance equation in the out-of-plane direction with finite element discretization. The computed problems are unidirectional plate bending, plate saddle deformation, and pressurized cylindrical and spherical shells. We use the neo-Hookean and Fung’s material models, for the compressible- and incompressible-material cases, and with the out-of-plane normal stress and without, which is the plane-stress case.
In Sect. 2, we provide the definitions and concepts used in the shell model, including the notations and main assumptions. In Sect. 3, we derive the weak form from the virtual-work principle and express the corresponding strong form. In Sect. 4, we describe the solution technique for the out-of-plane deformation, which is meant to be used only for the test computations in Sect. 5. The concluding remarks are given in Sect. 6. In the Appendix, we provide some supplemental derivations and the constitutive models.
2 Hyperelastic shell model
2.1 Kinematics
Let \(\varOmega _t\subset \mathbb {R}^{n_{\mathrm {sd}}}\) be the spatial domain with boundary \(\varGamma _{t}\) at time \(t \in (0,T)\), where \({n_{\mathrm {sd}}}\) is the number of space dimensions. Here, we assume \({n_{\mathrm {sd}}}= 3\). The subscript t indicates the time-dependence of the domain.
We split the domain as \(\varOmega _t = \overline{\varGamma }_t\times \left( h_\mathrm {th}\right) _t\), where \(\overline{\varGamma }_t\) represents the midsurface, which is parametrized by \({n_{\mathrm {pd}}}= {n_{\mathrm {sd}}}- 1\), with \({n_{\mathrm {pd}}}\) being the number of parametric dimensions. The remaining parametric direction is the out-of-plane direction, which we will explain a little later in this section. The symbol \(\left( h_\mathrm {th}\right) _t\) will represent both the shell thickness and the domain in the out-of-plane direction, depending on the context. With the position \(\overline{\mathbf {x}} \in \overline{\varGamma }_t\), we define a natural coordinate system:
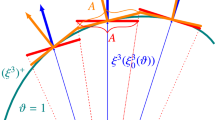
where \(\alpha = 1, \ldots , {n_{\mathrm {pd}}}\) and \(\xi ^\alpha \) represents the parametric space. Figure 1 shows a schematic shell domain. We note that this parametric space is only for representing the neighborhood around a point. With a range \(-1 \le \xi ^\alpha \le 1\) and without loss of generality, it can be seen as a parent finite element domain. The out-of-plane direction is
The components of the metric tensor are
and this is known as the first fundamental form. We also work with the contravariant components of the metric tensor \(\overline{g}^{\alpha \beta }\) and the contravariant basis vectors \(\overline{\mathbf {g}}^\alpha \) (see Appendix A for their relationship to \(\overline{g}_{\alpha \beta }\) and \(\overline{\mathbf {g}}_\alpha \)).
A schematic shell domain \(\varOmega _t\) at current configuration and the midsurface \(\overline{\varGamma }_t\). The black-framed region is for showing the parametric space used in representing the neighborhood around a point. With a range \(-1 \le \xi ^\alpha \le 1\), the parametric space can be seen as a parent finite element domain. The basis vectors of the natural coordinate system are also shown in the figure
A position \(\mathbf {x} \in \varOmega _t\) is represented as
where \(\xi ^3 \in \left( h_\mathrm {th}\right) _t = [(\xi ^3)^-,\,(\xi ^3)^+]\). Along \(\xi ^3\), the basis vectors are represented as
where
See Appendix B.1 for the lines between Eqs. (8) and (9). With that, the metric tensor components in 3D space are
where
Remark 1
The symbols \(\overline{\kappa }_{\alpha \beta }\) and \(\overline{\omega }_{\alpha \beta }\) are for notational convenience.
We note that the curvature tensor is defined by
and the square of the curvature tensor is the tensor version of \(\overline{\omega }_{\alpha \beta }\):
We also use the dual basis system with \(g^{\alpha \beta }\) and \(\mathbf {g}^\alpha \) (see Appendix A for their relationship to \(g_{\alpha \beta }\) and \(\mathbf {g}_\alpha \)).
We now provide similar definitions and derivations for the undeformed configuration \(\overline{\mathbf {X}} \in \overline{\varGamma }_0\). We start with the basis vectors
where \(\xi ^\alpha _0 = \xi ^\alpha \), and
We also again work with the contravariant components of the metric tensor \(\overline{G}^{\alpha \beta }\) and the contravariant basis vectors \(\overline{\mathbf {G}}^\alpha \) (see Appendix A for their relationship to \(\overline{G}_{\alpha \beta }\) and \(\overline{\mathbf {G}}_\alpha \)).
A position \(\mathbf {X} \in \varOmega _0\) is expressed as
where \(\xi ^3_0 \in \left( h_\mathrm {th}\right) _0 = [(\xi ^3_0)^-,\ (\xi ^3_0)^+]\). Similar to what we had for the current configuration, along \(\xi ^3_0\), the basis vectors are represented as
where
The lines between Eqs. (23) and (24) are the deformed-configuration counterpart of the lines between Eqs. (8) and (9). The metric tensor components in 3D space are
where
We also again use the dual basis system with \(G^{\alpha \beta }\) and \(\mathbf {G}^\alpha \) (see Appendix A for their relationship to \(G_{\alpha \beta }\) and \(\mathbf {G}_\alpha \)).
2.1.1 Deformation gradient tensor
The deformation gradient tensor \(\mathbf {F}\) is defined from
which implies
Using the relationship \(\xi ^\alpha = \xi ^\alpha _0\) and introducing
we can write
2.1.2 Cauchy–Green deformation tensor
The Cauchy–Green deformation tensor is defined as
which is
and the determinant of \(\mathbf {C}\) gives the square of \(J = \det \mathbf {F}\):
2.1.3 Green–Lagrange strain tensor
The Green–Lagrange strain tensor is defined as
where \(\mathbf {I}\) is the identity tensor, and one of the ways to express it is
We can then write \(\mathbf {E}\) as
The covariant components of the in-plane strain tensor are
The symbol \(\overline{\varepsilon }_{\alpha \beta }\) here represents what is typically identified as the membrane strain. That is only part of the membrane strain in our model. The normal component associated with the out-of-plane direction is
Remark 2
The term of Eq. (46) that is quadratic in \(\xi ^3\) and \(\xi ^3_0\) was omitted in [5] as a higher-order term. We retain that here.
2.2 The strain-energy density function
We express the strain-energy density function as
The second Piola–Kirchhoff stress tensor,
is obtained from
and from that and Eq. (41),
The Cauchy stress tensor, defined in the current configuration, can be obtained from
3 Variational formulation
The variations of the internal and kinetic energies are expressed as
where \(\rho _0\) is the density at the undeformed configuration. The principle of virtual work can then be written as
where \(\delta W_{\mathrm {ext}}\) is the external-force virtual work, explained more later.
Remark 3
We note that in [9] (Section 1.2.2), \(- \delta W_{\mathrm {int}}\) is used in place of \(\delta U\).
Remark 4
We also note that in [9] (Section 1.2.2), the variation of the kinetic energy, expressed in terms of the acceleration, is part of the external-force virtual work. Here we keep that separate. With this separation, Eq. (55) can be seen as d’Alembert’s principle.
Remark 5
With the displacement expressed as \(\mathbf {y}= \mathbf {x} - \mathbf {X}\), we can do the substitutions \(\dot{\mathbf {x}} = \dot{\mathbf {y}}\) and \(\ddot{\mathbf {x}} = \ddot{\mathbf {y}}\).
3.1 Admissible variations
The variation of \(\mathbf {x}\) is obtained by taking the variation of Eq. (6):
The variation \(\delta \overline{\mathbf {x}}\) represents the virtual displacement of the midsurface, \(\delta \overline{\mathbf {n}}\) represents the rotation of the midsurface (see Appendix B.2), and \(\delta \xi ^3\) represents the virtual displacement in the out-of-plane direction, relative to the midsurface.
From the variation of Eqs. (8) and (32), we obtain
The variation of \(\mathbf {E}\) can be obtained by taking the variation of Eqs. (46) and (47):
Remark 6
In [5], only the first two terms of Eq. (59) were present.
The expressions for the three variations in Eq. (59) can be written, from Eqs. (46), (10) and (13), as
Remark 7
As can be seen from the expressions in Eqs. (61), (62) and (63), the three variations are not independent. The variation \(\delta \overline{\omega }_{\alpha \beta }\) can be expressed in terms of \(\delta \overline{\varepsilon }_{\alpha \beta }\) and \(\delta \overline{\kappa }_{\alpha \beta }\). That can be done by first taking the variation of Eq. (14):
Next, \(\delta \overline{g}^{\gamma \delta }\) is written as
which can be derived by taking the variation of
As the last steps, from Eqs. (65) and (46), we write
substitute that into Eq. (64), and obtain
3.2 Variation of the strain energy
In one of the ways to express the variation of the strain energy, we start with
Because \(\mathbf {S}\) is a symmetric tensor, we simply write
Substituting Eq. (33), its variation, and Eq. (49) into this, we get
Substituting Eq. (57) into that, we obtain
We perform the integration in Eq. (53) with the integrand given by Eq. (73):
We define \(\mathbf {p}^\alpha \) as
its integration along \((h_\mathrm {th})_0\) as
and its first moment as
With these definitions, we write Eq. (74) in a simpler form:
We also express \(\delta U\) in an alternative form by using Eqs. (59), (60) and (49) in Eq. (53):
where the zeroth, first, and second moments of the contravariant components of \(\mathbf {S}\) are given as
Remark 8
In [5], the third integral in Eq. (79) was omitted.
Remark 9
The fourth, fifth, and sixth integrals in Eq. (79) are the contributions to the virtual work in the out-of-plane direction, which will be explained more in Sect. 3.5.
3.3 Variation of the kinetic energy
Performing the integration in Eq. (54), we get
Substituting Eq. (56) into this, we obtain
where
Remark 10
We note that
where
and \(\overline{\mathbf {n}}\times \hat{\mathbf {m}}_{1}\) represents the time derivative of the angular momentum. The derivation of Eq. (87) is given in Appendix B.3. This rearrangement may make it easier to see the fundamental mechanics in the term.
Remark 11
The second integral in Eq. (84) is related to the time derivative of the angular momentum. It was included in [41], but we did not see other papers that explicitly mention the inclusion of the term.
The acceleration is written as
Remark 12
We omit the time derivatives of \(\xi ^3\):
Otherwise they need to be stored. We see this approximation as a quasi-steady-state assumption.
With that, approximated forms of Eqs. (85) and (86) are written as
where
In the third term of Eq. (84), the integration along \((h_\mathrm {th})_0\) can be written, with Eq. (91), as
where
which are the variation of Eqs. (95) and (96). From Eqs. (97) to (98), we used
which can be obtained from \(\overline{\mathbf {n}}\cdot \dot{\overline{\mathbf {n}}} = 0\).
Remark 13
The second term in Eq. (98) represents the effect of the centripetal acceleration.
Remark 14
Because we omitted \(\dot{\xi }^3\) in obtaining Eq. (91), the Coriolis effect is neglected in Eq. (98).
Substituting Eq. (98) into Eq. (84), we obtain
3.4 The external virtual work
We separate \(\delta W_{\mathrm {ext}}\) into three parts:
where
Here \(S_t\) (see Fig. 2) is the edge line that traverses the edge surface as \(\xi ^3\) varies from \((\xi ^3)^-\) to \((\xi ^3)^+\). The symbol \(\mathbf {h}\) represents the traction, for all surfaces, including the edge surfaces.
A schematic undeformed-shell midsurface \(\overline{\varGamma }_0\) with edge \(\overline{S}_0\) and how a piece is cut from the shell domain to show the edge surface details (top). Enlarged view of the cut piece, showing also the upper and lower surfaces \(\varGamma ^+_0\) and \(\varGamma ^-_0\) (middle). Deformed-configuration cut piece, with \(\overline{\varGamma }_t\), \(\overline{S}_t\), \(\varGamma ^+_t\), and \(\varGamma ^-_t\) denoting the deformed-configuration counterparts of \(\overline{\varGamma }_0\), \(\overline{S}_0\), \(\varGamma ^+_0\), and \(\varGamma ^-_0\), and the edge line \(S_t\) that traverses the edge surface as \(\xi ^3\) varies from \((\xi ^3)^-\) to \((\xi ^3)^+\) (bottom)
Substituting Eq. (56) into Eq. (104) and using Eqs. (94), (95) and (99), we obtain
Substituting Eq. (56) into Eq. (105), we obtain
and the normal tractions as
We note that we can see \(\hat{p}\) as the pressure brought to the midsurface by using the area ratios.
Remark 15
In Eq. (108), there are three integrals. In [5], only the first integral was considered, and even in that, the evaluations were not based on the actual upper and lower surfaces as how it was done with Eqs. (109) and (110). The tractions acting on the upper and lower surfaces were treated as if they were acting on the midsurface. Not being able to use the correct surfaces was a consequence of the plane-stress assumption.
Remark 16
The terms in the second line of Eq. (108) can be written as \(\delta \overline{\mathbf {n}}\cdot \hat{\mathbf {h}}_{1}^- = \delta \overline{\mathbf {r}}\cdot (\overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^-)\) and \(\delta \overline{\mathbf {n}}\cdot \hat{\mathbf {h}}_{1}^+ = \delta \overline{\mathbf {r}}\cdot (\overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^+)\) (see Appendix B.3). We note that \(\overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^-\) and \(\overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^+\) represent the moment. Again these rearrangements may make it easier to see the fundamental mechanics in the terms. In a typical shell formulation, the distance between the upper and lower surfaces is not taken into account. Therefore, the tractions on those surfaces, even when they have shear components, do not produce moment.
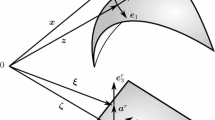
For the representation at the edges, we introduce a unit vector \(\overline{\mathbf {T}}\) along \(\overline{S}_0\) (see Fig. 3). The contravariant components are denoted as
The cut piece in Fig. 2 (middle) with the unit vectors \(\overline{\mathbf {N}}\), \(\overline{\mathbf {T}}\), and \(\mathbf {T}\)
We map \(\overline{\mathbf {T}}\) from the midsurface to the \(\xi _0^3\) surface with edge \(S_0\), and make a unit vector from that:
Using Eqs. (24), (26) and (27), \(\mathbf {T}\) can be expressed as
and its contravariant components are denoted as
We note that the numerator of Eq. (119) is coming from the numerator Eq. (116). For notational convenience, we define
From Eqs. (121) to (122), we used Eq. (119). We use the symbol \(\overline{L}_0\) to denote \(L_0\) at the midsurface, obtained by setting \(\xi ^3_0 = 0\):
This can be seen as the length counterpart of \(A_0\) given in Eq. (40). Using Eqs. (119), (122) and (123), we get
Similarly, we introduce unit vectors \(\overline{\mathbf {t}}\) and \(\mathbf {t}\) along \(\overline{S}_t\) and \(S_t\) (see Fig. 4). The stretch \(\lambda _\mathrm {T}\) along \(S_0\) is obtained from
Taking the inner product of \(\mathbf {g}^\alpha \) with both sides of Eq. (126), we obtain
Because \(\mathbf {t}\) is a unit vector, \(g_{\alpha \beta } t^\alpha t^\beta = 1 \) can be used to calculate \(\lambda _\mathrm {T}\) as
Similar to what we did for the undeformed configuration, we define
which is the length counterpart of A given in Eq. (39). Using Eqs. (129), (127) and (121), we get
and at the midsurface,
The cut piece in Fig. 2 (bottom) with the unit vectors \(\overline{\mathbf {n}}\), \(\overline{\mathbf {t}}\), and \(\mathbf {t}\)
We now define a unit outward normal vector for \(S_0\):
and for \(\overline{S}_0\):
Figure 5 shows the unit vectors \(\overline{\mathbf {B}}\) and \(\mathbf {B}\) and the rest of the unit vectors in the undeformed configuration.
The cut piece in Fig. 3 with the unit vectors \(\overline{\mathbf {B}}\) and \(\mathbf {B}\)
Then, corresponding to \(\mathbf {B}\), we introduce a unit vector \(\mathbf {b}\) in the deformed configuration, and the stretch in the direction of \(\mathbf {B}\) is obtained from
With Eq. (134) and \(\left\| \mathbf {b}\right\| = 1\), the stretch can be written as
We use the symbols \(\overline{\mathbf {b}}\) and \(\overline{\lambda }_\mathrm {B}\) to denote \(\mathbf {b}\) and \(\lambda _\mathrm {B}\) at midsurface:
and similarly write the stretch \(\overline{\lambda }_\mathrm {B}\) as
Remark 17
We note that, unlike \(\overline{\mathbf {B}}\), the unit vector \(\overline{\mathbf {b}}\) is not necessarily normal to \(\overline{S}_t\), and therefore \(\overline{\mathbf {t}}\cdot \overline{\mathbf {b}}\) does not have to be zero. To overcome the difficulty with using non-orthogonal basis vectors, we introduce the dual basis vectors:
We refer to Appendix C.1 for more on these.
Figure 6 shows the vectors \(\overline{\mathbf {t}}^\star \) and \(\overline{\mathbf {b}}^\star \), the unit vector \(\overline{\mathbf {b}}\), and some of earlier-defined unit vectors in the deformed configuration.
The cut piece in Fig. 4 with the unit vector \(\overline{\mathbf {b}}\) and the dual basis vectors \(\overline{\mathbf {t}}^\star \) and \(\overline{\mathbf {b}}^\star \)
With the ratio of the lengths along \(S_t\) and \(\overline{S}_t\) being \(L/\overline{L}\), we change the order of the integration in Eq. (106):
With the ratio of the lengths along \(\overline{S}_t\) and \(\overline{S}_0\) being \(\overline{L}/\overline{L}_0\) and with Eq. (130), we transform the first integration from the current to undeformed configuration:
Using Eq. (32), we transform the second integration from the current to undeformed configuration:
Substituting Eq. (56) into this, we get
We define \(\hat{\mathbf {h}}_{0}^\mathrm {e}\) as
and its first moment as
With these definitions, we write Eq. (143) in a simpler form:
We omit the variation of \(\xi ^3\):
Remark 18
The reasons for omitting the variation of \(\xi ^3\) in Eq. (146) are, (i) the out-of-plane shear stress is not meant to be represented in this model, and (ii) we already omitted the time derivatives of \(\xi ^3\) (see Remark 12).
Remark 19
The second integrand in Eq. (147) can be written as \(\delta \overline{\mathbf {n}}\cdot \hat{\mathbf {h}}_{1}^\mathrm {e} = \delta \overline{\mathbf {r}}\cdot \left( \overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^\mathrm {e}\right) \). We note that \(\overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^\mathrm {e}\) represents the moment.
3.5 The virtual work in the out-of-plane direction and the corresponding strong form
We substitute \(\delta U\) given by Eq. (79), \(\delta T\) given by Eq. (102), and \(\delta W_{\mathrm {ext}}\) given by Eqs. (103), (107), (108) and (147) into Eq. (55), exclude the variations associated with the midsurface, and obtain
We substitute Eq. (58) into this and consider only the out-of-plane variations at a given midsurface point:
Applying integration by parts to the last integral on the left-hand side, we obtain
We substitute Eqs. (99) and (100) into this, and the equation holds for all admissible \(\delta \xi ^3\). From that, we obtain the strong form:
and
Integrating Eq. (151) from \((\xi _0^3)^-\) to \((\xi _0^3)^+\) and using Eqs. (152) and (153), we obtain
We rearrange this equation by substituting for \(\hat{p}^-\) and \(\hat{p}^+\) from Eqs. (113) and (114), using the expression for \(\hat{S}_{\varepsilon }^{\alpha \beta }\) and \(\hat{S}_{\kappa }^{\alpha \beta }\) from Eqs. (80) and (81), and using Eqs. (92) and (101):
3.6 The virtual work for the midsurface deformation and the corresponding strong form
We substitute \(\delta U\) given by Eq. (78), \(\delta T\) given by Eq. (102), and \(\delta W_{\mathrm {ext}}\) given by Eqs. (103), (107), (108) and (147) into Eq. (55), exclude the out-of-plane variations, and obtain
where
Equation (156) is our weak form for the midsurface representation. To understand it better, we substitute
into it, apply integration by parts to the first and third integrals, and obtain
We note that, as shown in Fig. 5, the unit outward normal vector for \(\overline{S}_0\) is \(\overline{\mathbf {B}}\). With \(\delta \overline{\mathbf {n}}\) involving derivatives, we next apply integration by parts to the second and fourth lines of Eq. (161). We do that by using two expressions derived in Appendix C, given by Eqs. (306) and (316). After that, separating \(\delta \overline{\mathbf {x}}\) into its normal and tangential components, we obtain
We note that \(\hat{\mathbf {p}}_0^\alpha \) and \(\hat{\mathbf {p}}_1\) have only in-plane components; \(\overline{\mathbf {n}}\cdot \hat{\mathbf {p}}_0^\alpha = 0\) and \(\overline{\mathbf {n}}\cdot \hat{\mathbf {p}}_1^\alpha = 0\) (see Eqs. (75), (76) and (77)). With that, we get


Using Eq. (164), we rewrite Eq. (162) as
From that, the strong form in \(\overline{\varGamma }_0\) can be written as
We note that we split the strong form into its parts associated with the normal and in-plane directions. Along the boundary \(\overline{S}_0\), we have
Here Eqs. (168) and (169) are the parts associated with the normal and in-plane directions.
Remark 20
We can show that the first two terms of Eq. (166) constitute an alternative form of Eq. (155) and therefore give zero. For that, we rewrite \(\hat{\mathbf {p}}_0^\alpha \) by using Eqs. (76), (75) and (8):
take the inner product of both sides of that with \(-\overline{\mathbf {n}}_{, \alpha }\) , and obtain
We rearrange that by using Eqs. (264) and (13):
Recognizing the terms on the right-hand side from Eqs. (80) and (81), we get
With that and Eq. (157), Eq. (155) can be rewritten as
Combining that with Eq. (166), we obtain
The equation above represents the rotational balance around the midsurface.
Remark 21
Equation (170) represents the rotation boundary condition along \(\overline{S}_0\). It is a single-component equation. To determine which component that is, we start with taking the cross product of both sides of Eq. (145) with \(\overline{\mathbf {n}}\):
and recognizing the right-hand side as the moment acting along \(\overline{S}_0\). Using Eq. (139), Eq. (170) can be written as
which can be rearranged as
This means that Eq. (170) represents the tangential component of the rotation boundary condition along \(\overline{S}_0\). We note that we cannot have a component in the \(\overline{\mathbf {n}}\) direction because \( \left( \overline{\mathbf {n}}\times \hat{\mathbf {h}}_{1}^\mathrm {e} \right) \cdot \overline{\mathbf {n}}= 0, \) and we cannot have a component in the \(\overline{\mathbf {b}}^\star \) direction because of the Kirchhoff–Love assumption.
4 Stress and strain distributions in the out-of-plane direction
We solve for the stress and strain distributions along the out-of-plane direction at a given midsurface point. We use the symbol \(y^3\) to denote the displacement in the out-of-plane direction:
and write
The point on the midsurface is like an integration point in a typical finite element formulation. For simplicity, we assume steady state and exclude the body force. In the test computations, which will be reported in Sect. 5, we found out that determining in advance the midsurface variables needed in the equation associated with the out-of-plane direction is not a good path. Therefore, in this section, we treat also \(\overline{\varepsilon }_{\alpha \beta }\) and \(\overline{\kappa }_{\alpha \beta }\) as unknowns, with total six components. Then, in addition to Eq. (148), we use the first three integrals of \(\delta U\) given by Eq. (79), which are associated with the midsurface deformation, with \(\delta \overline{\varepsilon }_{\alpha \beta }\) and \(\delta \overline{\kappa }_{\alpha \beta }\) generating six additional equations. We note that other virtual-work terms in Eq. (55) play no role in the midsurface deformation. That is because \(\delta T= 0\) from assuming steady state, and in \(\delta W_{\mathrm {ext}}\), \(\delta W_{\mathrm {exbody}}= 0\) from excluding the body force, \(\delta W_{\mathrm {exsurf}}= 0\) from being for the upper and lower surfaces, and \(\delta W_{\mathrm {exedge}}= 0\) from being for the edge surfaces. We also note that \(\delta \overline{\omega }_{\alpha \beta }\) appearing in the third integral of Eq. (79) can be represented in terms of \(\delta \overline{\varepsilon }_{\alpha \beta }\) and \(\delta \overline{\kappa }_{\alpha \beta }\), as described in Remark 7. Some of the six additional equations will be removed for consistency with the constraints coming from the boundary conditions or geometry, depending on the problem setup.
Remark 22
In the actual computations, which will be presented in the second part of this two-part article, we plan to use a different way of numerically solving the strong form of the equations in the out-of-plane direction. That will involve change of unknown variable. We expect that coupling that solution process with solving for the midsurface deformation will not be computationally burdensome.
At this point, we will change the symbol we use for representing the variation associated with the virtual work, and call it “\(\delta _a\).” That is because in solving the nonlinear equations with the Newton–Raphson method, we will need to take another variation for the linearization in the iterations, and that variation will be denoted by the symbol \(\delta _b\). In other words, the linearization for the Newton–Raphson iterations will be in terms of \(\delta _b\). Using the test functions of \(\delta _a \xi ^3\), \(\delta _a \overline{\varepsilon }_{\alpha \beta }\), and \(\delta _a \overline{\kappa }_{\alpha \beta }\), we form the equation system as
where
We note that the undeformed shape is represented by \(\overline{G}_{\alpha \beta }\) and \(\overline{K}_{\alpha \beta }\), and the current configuration by \(\overline{\varepsilon }_{\alpha \beta }\) and \(\overline{\kappa }_{\alpha \beta }\).
Remark 23
The idea of representing the undeformed shape in terms of the metric tensor is from [42], and in that context the configuration is called the integration-point based zero-stress state (IPBZSS). In the shell model, full representation of the IPBZSS requires also the curvature tensor.
Remark 24
The variables \(\overline{\omega }_{\alpha \beta }\) and \(\delta _a \overline{\omega }_{\alpha \beta }\) appear in Eq. (183) for notational convenience. They are not independent variables. We can write \(\overline{\omega }_{\alpha \beta }\) as given by Eq. (14), and write \( \frac{1}{2} \delta _a \overline{\omega }_{\alpha \beta } \hat{S}_{\omega }^{\alpha \beta } \) by multiplying \(\delta _a \overline{\omega }_{\alpha \beta }\) given by Eq. (68) with \(\frac{1}{2} \hat{S}_{\omega }^{\alpha \beta }\):
We also note that
which follows from Eq. (45), and
which follows from Eq. (254) in Appendix A.
In describing the linearization for the Newton–Raphson iterations, we will first derive the variations needed for that. We start with the variations of \(S^{\alpha \beta }\) and \(S^{3 3}\):
where
The elastic moduli \(\mathbb {C}^{\alpha \beta \gamma \delta }\), \(\mathbb {C}^{\alpha \beta 3 3}\), \(\mathbb {C}^{3 3\gamma \delta }\), and \(\mathbb {C}^{3 3 3 3}\) can be derived from \(\varphi \). In Eqs. (59) and (60), using \(\delta _b\) in place of \(\delta \), recognizing that \(\delta \xi ^3\) and \(\delta y^3\) are in interchangeable, and reordering the terms, we obtain
and
Taking the variation of Eq. (181), we obtain
From the variations of Eqs. (80), (81) and (82), we obtain
Now that we have all the variations we need, we write \(\delta _b N\) by taking the variation of Eq. (183). After taking the variation, we substitute into it Eqs. (198), (200) and (202). Then we substitute Eqs. (188), (189), (190), (191), (192), (193) and (196) into that. Also, we recognize the right-hand sides of Eqs. (195) and (197) and \(\delta _a\) versions of those. At the end, we get
Remark 25
The choices made between using different combinations of variable in Eq. (203) were driven by having visible symmetry in \(\delta _a\) and \(\delta _b\) and reducing the number of terms.
Remark 26
The term \(\delta _a \delta _b \overline{\omega }_{\alpha \beta }\) is not zero, because, as explained in Remark 23, \(\delta _a \overline{\omega }_{\alpha \beta }\) is not an independent variation. We replace \(\delta \) with \(\delta _a\) in Eq. (68), take its \(\delta _b\) variation, multiply that with \(\frac{1}{2} \hat{S}_{\omega }^{\alpha \beta }\), and obtain
Remark 27
When the traction conditions on the upper and lower surfaces are coming from the pressure on those surfaces, with the conditions expressed as
\(\hat{p}^-\) and \(\hat{p}^+\) appearing in Eq. (184) can vary because of the midsurface deformation or the displacement in the out-of-plane direction. We can derive an expression for that from Eqs. (113) and (114) by using Eqs. (109), (110), (205) and (206):
We note that A depends on both the midsurface deformation and the displacement in the out-of-plane direction. We derive the expression for \(\delta _b A\) based on that dependence and use it in the computations.
5 Test problems
With the method described in Sect. 4, for a set of test problems, we determine the displacement in the out-of-plane direction. In all cases, we use a uniform finite element mesh made of 200 elements with linear functionsFootnote 1. The lower or inner surface servesFootnote 2 as the “midsurface.” Together with the out-of-plane displacement, the midsurface variables \( \overline{\varepsilon }_{\alpha \beta }\) and \(\overline{\kappa }_{\alpha \beta }\) are solved for, with different boundary or geometry conditions depending on the problem setup. For comparison, we include in the tests a plane-stress shell model from [5]. The constitutive models, provided in Appendix D, are neo-Hookean and Fung’s models with compressible and incompressible materials.
The stress-related variables are scaled by the shear modulus \(\mu _0\) at the undeformed configuration. The Poisson’s ratio \(\nu \) is defined based on the bulk modulus at the undeformed configuration, with \(\nu = 0.50\) indicating incompressible material. We use separate models for compressible and incompressible materials, but the compressible-material model converges to the incompressible-material model in the limit \(\nu \rightarrow 0.50\) (see [5]). The scaled stress components we report will be from the Cauchy stress, and the indices will correspond to the coordinate frame defined separately in each problem, but the index 3 will always imply the out-of-plane direction:
For the length scale, we use the undeformed shell thickness \(\left( h_\mathrm {th}\right) _0= (\xi ^3_0)^+ - (\xi ^3_0)^-\). We note that, with the shell model and method sections behind us, now we are using the symbol \(\left( h_\mathrm {th}\right) _0\) for the shell thickness, as we stated in Sect. 2.1 that we would. We also note that the current thickness is expressed as \(h_\mathrm {th}= (\xi ^3)^+ - (\xi ^3)^-\).
Unidirectional plate bending. Problem setup. The lower surface is serving as the midsurface. The bending moment M is applied along the midsurface edges. The nondimensional curvature \(\overline{\kappa }^*_1\) is given by Eq. (215)
We use the principal curvatures at the midsurface to describe the individual problems. The principal curvatures \(\overline{\kappa }_1\) and \(\overline{\kappa }_2\) are obtained from the generalized eigenvalue problem
where \(t^\beta \) represents the contravariant components of the principal curvature direction. From Eq. (212), we can get the principal curvatures as
Their nondimensional versions are
5.1 Unidirectional plate bending
The bending is only in \(\xi ^1\) direction (see Fig. 7). No traction is applied on the upper or lower surface. The bending moment M is applied along the midsurface edges. We select \(\overline{G}_\alpha \) to be unit orthogonal basis vectors, and consequently \(\overline{G}_{11} = \overline{G}_{22} = 1\), and \(\overline{G}_{12} = 0\). We note that, with this selection, we no longer have \(-1 \le \xi ^\alpha \le 1\). In this problem, because it is a plate, \(\overline{K}_{11} = \overline{K}_{22} = \overline{K}_{12} = 0\). We constrain the midsurface deformation with \(\overline{\varepsilon }_{22} = \overline{\varepsilon }_{12} = 0\) and \(\overline{\kappa }_{22} = \overline{\kappa }_{12} = 0\). With these conditions, from Eq. (213) we get
and its nondimensional version is
For any value of \(\overline{\kappa }^*_1 \), we set \(\overline{\kappa }_{11}\) based on that relationship, noting that \(\overline{g}^{11}\) is a function of \(\overline{\varepsilon }_{11}\). We solve for \(\overline{\varepsilon }_{11}\) together with the displacement in the out-of-plane direction. After that, we calculate the required moment around \(\xi ^3=0\):
and scale that as
In this problem, \(\frac{L}{\overline{L}~} = 1\) and \(g_{21} = 0\), which follow from the constraints listed earlier.
Figures 8 and 9 show, for the neo-Hookean and Fung’s materials, \(M^*\) as a function of \(\overline{\kappa }^*_1\). For both materials, the model with the plane-stress assumption (\(\sigma _{33} = 0\)) is behaving stiffer than the model with the out-of-plane normal stress (\(\sigma _{33} \ne 0\)). For the Fung’s material, the difference becomes smaller at higher \(\nu \) values.
We report, for \(\overline{\kappa }^*_1 = {\text {0.5 and 1}}\), \(\xi ^3_0\) profiles of different variables. We report \(\lambda _3\), \(J\), \(\sigma _{11}^*\), and \(\sigma _{33}^*\) in Figs. 10, 11, 12 and 13 for the neo-Hookean material, and in Figs. 14, 15, 16 and 17 for the Fung’s material. For the neo-Hookean material, \(\lambda _3\) obtained with the \(\sigma _{33} = 0\) model is more than it is with the \(\sigma _{33} \ne 0\) model. Assuming that the \(\sigma _{33} \ne 0\) model is giving the true solution, \(\sigma _{33} \le 0\). This means that the \(\sigma _{33} = 0\) model is behaving in a fashion that inhibits the compressive stress that should be there. The larger \(\lambda _3\) makes \(h_\mathrm {th}\) higher, and that could be the source of the stiffer response mentioned when Figs. 8 and 9 were discussed. Overall, the Fung’s material behaves similar to how the neo-Hookean material behaves. However, because of the strong nonlinearity, the \(\lambda _3\) profile is more complex. For example, there is a local maximum close to the inner surface. Also, at high values of \(\nu \), \(\sigma _{11}\) becomes very high at both the lower and upper surfaces. That is making \(\sigma _{33}\) higher.
To have a better understanding of the significance of \(\sigma ^*_{33}\), we scale it by using, in general, \(\left| \sigma _{11}^*\right| _{\max }\) and \(\left| \sigma _{22}^*\right| _{\max }\), where “max” denotes the maximum over both \(\xi ^3_0\) and \(\nu \). To be on the conservative side in not overrating that significance, we scale \(\sigma ^*_{33}\) with \(\sigma _{\mathrm {MAX12}}^*\) = \(\max \left( \left| \sigma _{11}^*\right| _{\max },\,\left| \sigma _{22}^*\right| _{\max }\right) \). We note that in this case \(\left| \sigma _{22}^*\right| _{\max } = 0\). Tables 1 and 2 show, for the neo-Hookean and Fung’s materials and for \(\overline{\kappa }^*_1 = {\text {0.5 and 1}}\), \(\left| \sigma _{11}^*\right| _{\max }\), \(\left| \sigma _{33}^*\right| _{\max }\), and \(\left. \left| \sigma _{33}^*\right| _{\max }\big /\sigma _{\mathrm {MAX12}}^*\right. \). We see that the significance, as measured by \(\left. \left| \sigma _{33}^*\right| _{\max }\big /\sigma _{\mathrm {MAX12}}^*\right. \), is more than 10 % for the neo-Hookean material and more than 5.9 % for the Fung’s material.
5.2 Plate saddle deformation
Bending moments are applied along the midsurface edges both in \(\xi ^1\) and \(\xi ^2\) directions to create a saddle deformation. No traction is applied on the upper or lower surface. Again, we select \(\overline{G}_{11} = \overline{G}_{22} = 1\), \(\overline{G}_{12} = 0\), and \(\overline{K}_{11} = \overline{K}_{22} = \overline{K}_{12} = 0\) to represent a plate. We constrain the midsurface deformation with \(\overline{\varepsilon }_{12} = 0\) and \(\overline{\kappa }_{12} = 0\). With these conditions, from Eqs. (213) and (214) we get
and their nondimensional versions are
For any values of \(\overline{\kappa }_1^*\) and \(\overline{\kappa }_2^*\), we set \(\overline{\kappa }_{11}\) and \(\overline{\kappa }_{22}\) based on these relationships, noting that \(\overline{g}^{11}\) is a function of \(\overline{\varepsilon }_{11}\) and \(\overline{g}^{22}\) is a function of \(\overline{\varepsilon }_{22}\). We solve for \(\overline{\varepsilon }_{11}\) and \(\overline{\varepsilon }_{22}\) together with the displacement in the out-of-plane direction.
The saddle deformation is obtained by specifying the two principal curvatures to be \(\overline{\kappa }^*_1 > 0\) and \(\overline{\kappa }^*_2 < 0\). The curvature at the upper surface can be written as
and this needs to be finite. That requirement brings the restriction \(\overline{\kappa }_2 h_\mathrm {th}= \overline{\kappa }_2^* \frac{h_\mathrm {th}}{\left( h_\mathrm {th}\right) _0} > - 1\). Considering that, we set \(\overline{\kappa }^*_2 = - \frac{1}{2}\).
We report, for the two test cases given in Table 3, \(\xi ^3_0\) profiles of \(\lambda _3\), \(J\), \(\sigma _{11}^*\), \(\sigma _{22}^*\), and \(\sigma _{33}^*\). Figures 18, 19, 20, 21 and 22 show those profiles for the neo-Hookean material, and Figs. 23, 24, 25, 26 and 27 for the Fung’s material.
Case 2 is closer to having \(\kappa _1^* = - \kappa _2^*\) at \(\xi _0^3/\left( h_\mathrm {th}\right) _0= 0.5\). This is the reason behind the near symmetry between the \(\sigma _{11}^*\) and \(\sigma _{22}^*\) profiles (see Case 2 of Figs. 20 and 21, and Case 2 of Figs. 25 and 26). Looking at the \(\lambda _3\) profiles (see Figs. 18 and 23), there is more difference between what we get from the \(\sigma _{33} \ne 0\) and \(\sigma _{33} = 0\) models than between what we get from different \(\nu \) values. In other words, the shell models being different is more significant than the \(\nu \) values being different. Tables 4 and 5 show, for the neo-Hookean and Fung’s materials and for Case 1 and Case 2, \(\left| \sigma _{11}^*\right| _{\max }\), \(\left| \sigma _{22}^*\right| _{\max }\), \(\left| \sigma _{33}^*\right| _{\max }\), and \(\left. \left| \sigma _{33}^*\right| _{\max }\big /\sigma _{\mathrm {MAX12}}^*\right. \). This time \(\left. \left| \sigma _{33}^*\right| _{\max }\big /\sigma _{\mathrm {MAX12}}^*\right. \) is more than 16 % for the neo-Hookean material and more than 6.2 % for the Fung’s material. These numbers are higher compared to what we had in the unidirectional plate bending.
5.3 Pressurized cylindrical and spherical shells
The inner and outer pressures are \(p_\mathrm {I}\) and \(p_\mathrm {O}\), and the inner and outer radii are \(R_\mathrm {I}\) and \(R_\mathrm {O}\) in the undeformed configuration and \(r_\mathrm {I}\) and \(r_\mathrm {O}\) in the deformed configuration (see Fig. 28). We note that \(R_\mathrm {O} = R_\mathrm {I} + \left( h_\mathrm {th}\right) _0\) and \(r_\mathrm {O} = r_\mathrm {I} + h_\mathrm {th}\). We set \(\frac{\left( h_\mathrm {th}\right) _0}{2 R_\mathrm {I}} = 0.1\), the same value used for the undeformed configurations in [5].
Pressurized cylindrical and spherical shells. The symbols \(p_\mathrm {I}\) and \(p_\mathrm {O}\) represent the pressures acting on the inner and outer surfaces in the actual problem. The symbols \(r_\mathrm {I}\) and \(r_\mathrm {O}\) represent the inner and outer radii in the deformed configuration, and \(R_\mathrm {I}\) and \(R_\mathrm {O}\) in the undeformed configuration
We compute with three different methods, characterized by selecting between the \(\sigma _{33} \ne 0\) and \(\sigma _{33} = 0\) models and whether \(p_\mathrm {O}\) is applied at the outer or inner surface (see Table 6). In Method 1, by applying both \(p_\mathrm {I}\) and \(p_\mathrm {O}\) at the inner surface, which serves as the midsurface, the difference between the inner and outer surface areas is not taken into account in calculating the net force acting on the shell. That is taken into account in Method 2 by applying \(p_\mathrm {O}\) at the outer surface. Method 3 also takes that into account, but with the \(\sigma _{33} \ne 0\) model. We measure the deformation by \(\overline{\lambda }_1\). For the cylindrical shell, we set \(\lambda _2 = 1\). We set \(p_\mathrm {I} = 2 p\) and \(p_\mathrm {O} = p\), and p is scaled as \(p^* = \frac{p}{\mu _0}\).
5.3.1 Pressurized cylindrical shell
We select the undeformed configuration as
and constrain the midsurface deformation with
In representing the mutual dependence between \(\overline{\kappa }_{11}\) and \(\overline{\varepsilon }_{11}\) based on the constraints above, we select the form \(\overline{\kappa }_{11}\) being a function of \(\overline{\varepsilon }_{11}\). We solve for \(\overline{\varepsilon }_{11}\) together with the displacement in the out-of-plane direction, with the conditions \(p_\mathrm {O}^* = p^*\) and \(p_\mathrm {I}^* = 2 p^*\) (see Remark 27 for the way the pressure conditions are specified).
Figures 29 and 30 show, for both the neo-Hookean and Fung’s materials, \(p^*\) as a function of \(\overline{\lambda }_1\). We first compare Method 1 and Method 2. With Method 1, because \(p_\mathrm {O}\) acts on the inner surface, the net force in the inflation direction is more. Consequently, in all cases, for a given \(p^*\), Method 1 has higher \(\overline{\lambda }_1\). Next we compare Method 2 and Method 3. For the neo-Hookean material, in all cases, for a given \(\overline{\lambda }_1\), Method 2 has higher \(p^*\), meaning that it is stiffer than Method 3. For the Fung’s material, we do not see that in all cases. When \(\nu = 0.5\), Method 2 is stiffer for all values of \(\overline{\lambda }_1\), but at lower \(\nu \) values, beyond a high-enough \(\overline{\lambda }_1\) value, Method 2 switches to being less stiff. We will discuss that more when we report the \(\xi ^3_0\) profiles.
Remark 28
It is clear from Figs. 29 and 30 that when \(\nu = 0.5\), for both the neo-Hookean and Fung’s materials, there is no \(\overline{\lambda }_1\) value that would make Method 2 less stiff. In other words, if the behavior is incompressible, Method 2, i.e. the \(\sigma _{33} = 0\) model, is stiffer.
We report, for \(\lambda _1 = 1.3\), \(\xi ^3_0\) profiles of \(\lambda _3\), \(J\), \(\sigma _{11}^*\), and \(\sigma _{33}^*\). Figures 31, 32, 33 and 34 show those profiles for the neo-Hookean material, and Figs. 35, 36, 37 and 38 for the Fung’s material. Because the only difference between Method 1 and Method 2 is how the net force acting on the midsurface is calculated, when we look at the \(\xi ^0_3\) profiles coming from the two methods at a given \(\overline{\lambda }_1\), meaning at the same midsurface deformation, we are already beyond how the net force acting on the midsurface was calculated. The midsurface deformations are the same, and therefore the \(\xi ^0_3\) profiles will be the same. For that reason, the \(\xi ^3_0\) profiles are reported under the labels “\(\sigma _{33} = 0\)” and “\(\sigma _{33} \ne 0\).”
When \(\nu =0.5\), the deformation patterns obtained with the \(\sigma _{33}=0\) and \(\sigma _{33} \ne 0\) models are the same (see Figs. 31, 32, 35, 36). This is expected because when \(\nu =0.5\), the constraint \(J=1\) determines the profile for a given midsurface deformation.
For the Neo-Hookean material, as can be seen in Fig. 33, the \(\sigma _{33} = 0\) model yields higher \(\sigma _{11}^*\) values at all \(\nu \) values and for the full range of \(\xi ^3_0\). Remembering that these profiles are for a given value of \(\lambda _1\), higher \(\sigma _{11}^*\) means that \(\sigma _{33} = 0\) model stiffer. This is consistent with the observation we made when we discussed Fig. 29.
For the Fung’s material, we do not see that in Fig. 37 at all \(\nu \) values. Consistent with the observation we made when we discussed Fig. 30, when \(\nu = 0.5\), the \(\sigma _{33}=0\) model yields higher \(\sigma _{11}^*\) values, and therefore is stiffer, for the full range of range of \(\xi ^3_0\). For this specific value of \(\overline{\lambda }_1\) we are reporting the \(\xi ^3_0\) profiles, the \(\sigma _{33}=0\) model is also stiffer when \(\nu = 0.49\) and for the full range of \(\xi ^3_0\). At lower \(\nu \) values, however, the \(\sigma _{33}=0\) model does not yield higher \(\sigma _{11}^*\) values for the full range of \(\xi ^3_0\), and at even lower \(\nu \) values, it yields lower \(\sigma _{11}^*\) values for the full range of \(\xi ^3_0\), and therefore is less stiff than the \(\sigma _{33} \ne 0\) model. This can be explained by the shifting balance between the bulk and shear moduli as \(\overline{\lambda }_1\) varies. At \(\nu \) values not far from 0.5, when \(\overline{\lambda }_1\) is not so high, the bulk modulus is dominant, the material behavior is closer to being incompressible, and therefore, from Remark 28, the \(\sigma _{33} = 0\) model is stiffer. However, even at \(\nu \) values not far from 0.5, due to the exponential form of the constitutive model, when \(\overline{\lambda }_1\) is high enough, the shear modulus is dominant and not the bulk modulus, the material behavior is not close enough to being incompressible, and therefore the \(\sigma _{33} = 0\) model is less stiff.
5.3.2 Pressurized spherical shell
We select the undeformed configuration as
and constrain the midsurface deformation with
In representing the mutual dependence between \(\overline{\kappa }_{11}\), \(\overline{\kappa }_{22}\), \(\overline{\varepsilon }_{22}\), and \(\overline{\varepsilon }_{11}\) based on the constraints above, we select the form \(\overline{\kappa }_{11}\), \(\overline{\kappa }_{22}\), and \(\overline{\varepsilon }_{22}\) being functions of \(\overline{\varepsilon }_{11}\). We solve for \(\overline{\varepsilon }_{11}\) together with the displacement in the out-of-plane direction, with the conditions \(p_\mathrm {O}^* = p^*\) and \(p_\mathrm {I}^* = 2 p^*\). Figures 39 and 40 show, for both the neo-Hookean and Fung’s materials, \(p^*\) as a function of \(\overline{\lambda }_1\). Our observations are essentially the same as those we made for the cylindrical shell, except the differences are more pronounced, because, with the same radius, the sphere has overall higher curvature effects.
We report, for \(\lambda _1 = 1.3\), \(\xi ^3_0\) profiles of \(\lambda _3\), \(J\), \(\sigma _{11}^*\), and \(\sigma _{33}^*\). Figures 41, 42, 43 and 44 show those profiles for the neo-Hookean material, Figs. 45, 46, 47 and 48 for the Fung’s material. We again note that the \(\xi ^0_3\) profiles coming from Method 1 and Method 2 at a given \(\overline{\lambda }_1\) will be the same and therefore the \(\xi ^3_0\) profiles are again reported under the labels “\(\sigma _{33} = 0\)” and “\(\sigma _{33} \ne 0\).” We note in Fig. 47 that, although it is not all discernible, except for the full range of \(\xi _0^3/\left( h_\mathrm {th}\right) _0\) when \(\nu =0.5\) and for \(\xi _0^3/\left( h_\mathrm {th}\right) _0> 0.5\) when \(\nu = 0.49\), the \(\sigma _{33} = 0\) model yields lower \(\sigma _{11}^*\) values and therefore is less stiff than the \(\sigma _{33} \ne 0\) model. The substance of the observations we made for the cylindrical shell remains applicable.
6 Concluding remarks
This was the first part of a two-part article on a hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress. We have presented the derivation of the new model, with focus on the mechanics of the out-of-plane deformation. To determine the out-of-plane stress, we solve the linear-momentum-balance equation in the out-of-plane direction. Accounting for the out-of-plane normal stress distribution in the out-of-plane direction affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the shell. The improvement is beyond what was achieved with the new model’s precursor [5] by accounting for the out-of-plane deformation mapping. Continuing what was started with the precursor, the new model is extending the range of applicability of the Kirchhoff–Love shell theory to the situations where the Kirchhoff–Love shell kinematics is still valid yet the thickness or the curvature change is significant enough to make a difference in the response.
By accounting for the out-of-plane normal stress, the traction acting on the shell can be specified on the upper and lower surfaces separately. This enables more accuracy in the linear-momentum balance in the out-of-plane direction. For example, we can accurately model cases that might have nonzero net force even when those out-of-plane tractions have equal magnitudes and opposite directions. Accounting for the out-of-plane normal stress also enables more accuracy in representation of the moment the shear tractions on the upper and lower surfaces generate around the midsurface. To accurately account for the moment generated by the separate shear tractions on the upper and lower surfaces, we have also improved the rotational kinematics in the model. Accounting for the out-of-plane stress improves the out-of-plane deformation mapping also in cases with no traction on the upper or lower surfaces and no body force. Those would be the cases when the shell deformation is driven by the displacements and slopes specified along the shell edges.
We presented test computations for unidirectional plate bending, plate saddle deformation, and pressurized cylindrical and spherical shells. We tested the neo-Hookean and Fung’s material models, for the compressible and incompressible materials, and with the out-of-plane normal stress and without, which is the plane-stress case. The test computations show that the differences between the shell models with and without the out-of-plane normal stress are more pronounced i) for plate saddle deformation than unidirectional plate bending, ii) when we have higher curvature effects, and iii) for cylindrical of spherical shells at high \(\nu \) values. We leave it to the reader to judge how significant these differences are.
The level of accuracy we are striving for in representing the tractions on the upper and lower surfaces would be meaningful in an FSI computation only if the flow solution method can deliver those tractions with a comparable level of accuracy. That level of flow solution accuracy, especially in representing the shear stress, requires moving-mesh methods, where the high mesh resolution near solid surfaces follows the fluid–solid interface as it moves. That is now possible even in flow computations with actual contact between solid surfaces or some other topology change. The space–time computational methods introduced in the last decade enable that, as can be seen, for example, in [43, 44].
Notes
As mentioned in Remark 22, in the actual computations, we will be using a different way of numerically solving the equations in the out-of-plane direction, and that process will involve an order of magnitude less number of points.
We note that, as can be inferred from the overall formulation, in the shell model proposed here, the location of the midsurface does not matter. However, it does in the model proposed in [5]. We will be comparing our results to those obtained with that model. This is the reason why the lower or inner surface serves as the midsurface.
References
Kiendl J, Bletzinger KU, Linhard J, Wüchner R (2009) Isogeometric shell analysis with Kirchhoff-Love elements. Comput Methods Appl Mech Eng 198:3902–3914
Kiendl J, Bazilevs Y, Hsu M-C, Wüchner R, Bletzinger K-U (2010) The bending strip method for isogeometric analysis of Kirchhoff-Love shell structures comprised of multiple patches. Comput Methods Appl Mech Eng 199:2403–2416
Bazilevs Y, Hsu M-C, Kiendl J, Wüchner R, Bletzinger K-U (2011) 3D simulation of wind turbine rotors at full scale. Part II: Fluid-structure interaction modeling with composite blades. Int J Numer Methods Fluids 65:236–253
Kiendl J, Hsu M-C, Wu MCH, Reali A (2015) Isogeometric Kirchhoff–Love shell formulations for general hyperelastic materials. Comput Methods Appl Mech Eng 291:280–303
Takizawa K, Tezduyar TE, Sasaki T (2019) Isogeometric hyperelastic shell analysis with out-of-plane deformation mapping. Comput Mech 63:681–700. https://doi.org/10.1007/s00466-018-1616-3
Bazilevs Y, Hsu M-C, Kiendl J, Benson DJ (2012) A computational procedure for pre-bending of wind turbine blades. Int J Numer Methods Eng 89:323–336
Bazilevs Y, Hsu M-C, Takizawa K, Tezduyar TE (2012) ALE-VMS and ST-VMS methods for computer modeling of wind-turbine rotor aerodynamics and fluid-structure interaction. Math Models Methods Appl Sci 22(supp02):1230002. https://doi.org/10.1142/S0218202512300025
Bazilevs Y, Hsu M-C, Scott MA (2012) Isogeometric fluid-structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Comput Methods Appl Mech Eng 24–9252:28–41
Bazilevs, Y, Takizawa K, Tezduyar TE (2013) Computational Fluid–Structure Interaction: Methods and Applications. Wiley, ISBN 978-0470978771
Bazilevs Y, Korobenko A, Deng X, Yan J (2015) Novel structural modeling and mesh moving techniques for advanced FSI simulation of wind turbines. Int J Numer Methods Eng 102:766–783. https://doi.org/10.1002/nme.4738
Takizawa K, Tezduyar TE, Kostov N (2014) Sequentially-coupled space-time FSI analysis of bio-inspired flapping-wing aerodynamics of an MAV. Comput Mech 54:213–233. https://doi.org/10.1007/s00466-014-0980-x
Hsu M-C, Kamensky D, Bazilevs Y, Sacks MS, Hughes TJR (2014) Fluid-structure interaction analysis of bioprosthetic heart valves: significance of arterial wall deformation. Comput Mech 54:1055–1071. https://doi.org/10.1007/s00466-014-1059-4
Hsu M-C, Kamensky D, Xu F, Kiendl J, Wang C, Wu MCH, Mineroff J, Reali A, Bazilevs Y, Sacks MS (2015) Dynamic and fluid-structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models. Comput Mech 55:1211–1225. https://doi.org/10.1007/s00466-015-1166-x
Wu MCH, Zakerzadeh R, Kamensky D, Kiendl J, Sacks MS, Hsu M-C (2018) An anisotropic constitutive model for immersogeometric fluid-structure interaction analysis of bioprosthetic heart valves. J Biomech 74:23–31
Xu F, Morganti S, Zakerzadeh R, Kamensky D, Auricchio F, Reali A, Hughes TJR, Sacks MS, Hsu M-C (2018) A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid-structure interaction analysis. Int J Numer Methods Biomed Eng 34:e2938
Kamensky D, Xu F, Lee C-H, Yan J, Bazilevs Y, Hsu M-C (2018) A contact formulation based on a volumetric potential: application to isogeometric simulations of atrioventricular valves. Comput Methods Appl Mech Eng 330:522–546
Bazilevs Y, Deng X, Korobenko A, di Scalea FL, Todd MD, Taylor SG (2015) Isogeometric fatigue damage prediction in large-scale composite structures driven by dynamic sensor data. J Appl Mech 82:091008
Deng X, Korobenko A, Yan J, Bazilevs Y (2015) Isogeometric analysis of continuum damage in rotation-free composite shells. Comput Methods Appl Mech Eng 284:349–372
Bazilevs Y, Korobenko A, Deng X, Yan J (2016) FSI modeling for fatigue-damage prediction in full-scale wind-turbine blades. J Appl Mech 83(6):061010
Bazilevs Y, Pigazzini MS, Ellison A, Kim H (2017) A new multi-layer approach for progressive damage simulation in composite laminates based on isogeometric analysis and Kirchhoff-Love shells. Part I: Basic theory and modeling of delamination and transverse shear. Comput Mech. https://doi.org/10.1007/s00466-017-1513-1
Pigazzini MS, Bazilevs Y, Ellison A, Kim H (2017) A new multi-layer approach for progressive damage simulation in composite laminates based on isogeometric analysis and Kirchhoff-Love shells. Part II: Impact modeling. Comput Mech. https://doi.org/10.1007/s00466-017-1514-0
Pigazzini MS, Bazilevs Y, Ellison A, Kim H (2018) Isogeometric analysis for simulation of progressive damage in composite laminates. J Compos Mater. https://doi.org/10.1177/0021998318770723
Benzaken J, Herrema AJ, Hsu M-C, Evans JA (2017) A rapid and efficient isogeometric design space exploration framework with application to structural mechanics. Comput Methods Appl Mech Eng 316:1215–1256
Herrema AJ, Wiese NM, Darling CN, Ganapathysubramanian B, Krishnamurthy A, Hsu M-C (2017) A framework for parametric design optimization using isogeometric analysis. Comput Methods Appl Mech Eng 316:944–965
Simo JC, Rifai MS, Fox DD (1990) On a stress resultant geometrically exact shell model. Part IV: variable thickness shells with through-the-thickness stretching. Comput Methods Appl Mech Eng 81:91–126
Bischoff M, Ramm E (1997) Shear deformable shell elements for large strains and rotations. Int J Numer Methods Eng 40:4427–4449
Pimenta PM, Campello EMB, Wriggers P (2004) A fully nonlinear multi-parameter shell model with thickness variation and a triangular shell finite element. Comput Mech 34:181–193
Klinkel S, Gruttmann F, Wagner W (2008) A mixed shell formulation accounting for thickness strains and finite strain 3d material models. Int J Numer Methods Eng 74:945–970
Ivannikov V, Tiago C, Pimenta PM (2014) On the boundary conditions of the geometrically nonlinear Kirchhoff-Love shell theory. Int J Solids Struct 51:3101–3112
Ivannikov V, Tiago C, Pimenta PM (2015) Generalization of the \(C^1\) TUBA plate finite elements to the geometrically exact Kirchhoff-Love shell model. Comput Methods Appl Mech Eng 294:210–244
Viebahn N, Pimenta PM, Schröder J (2016) A simple triangular finite element for nonlinear thin shells: statics, dynamics and anisotropy. Comput Mech 59:281–297
Tezduyar TE, Sathe S, Schwaab M, Conklin BS (2008) Arterial fluid mechanics modeling with the stabilized space-time fluid-structure interaction technique. Int J Numer Methods Fluids 57:601–629. https://doi.org/10.1002/fld.1633
Tezduyar TE, Schwaab M, Sathe S (2009) Sequentially-Coupled Arterial Fluid-Structure Interaction (SCAFSI) technique. Comput Methods Appl Mech Eng 198:3524–3533. https://doi.org/10.1016/j.cma.2008.05.024
Takizawa K, Christopher J, Tezduyar TE, Sathe S (2010) Space-time finite element computation of arterial fluid-structure interactions with patient-specific data. Int J Numer Methods Biomed Eng 26:101–116. https://doi.org/10.1002/cnm.1241
Tezduyar TE, Takizawa K, Moorman C, Wright S, Christopher J (2010) Multiscale sequentially-coupled arterial FSI technique. Comput Mech 46:17–29. https://doi.org/10.1007/s00466-009-0423-2
Takizawa K, Moorman C, Wright S, Christopher J, Tezduyar TE (2010) Wall shear stress calculations in space-time finite element computation of arterial fluid-structure interactions. Comput Mech 46:31–41. https://doi.org/10.1007/s00466-009-0425-0
Takizawa K, Moorman C, Wright S, Purdue J, McPhail T, Chen PR, Warren J, Tezduyar TE (2011) Patient-specific arterial fluid-structure interaction modeling of cerebral aneurysms. Int J Numer Methods Fluids 65:308–323. https://doi.org/10.1002/fld.2360
Tezduyar TE, Takizawa K, Brummer T, Chen PR (2011) Space-time fluid-structure interaction modeling of patient-specific cerebral aneurysms. Int J Numer Methods Biomed Eng 27:1665–1710. https://doi.org/10.1002/cnm.1433
Takizawa K, Brummer T, Tezduyar TE, Chen PR (2012) A comparative study based on patient-specific fluid-structure interaction modeling of cerebral aneurysms. J Appl Mech 79:010908. https://doi.org/10.1115/1.4005071
Takizawa K, Tezduyar TE, Buscher A, Asada S (2014) Space-time interface-tracking with topology change (ST-TC). Comput Mech 54:955–971. https://doi.org/10.1007/s00466-013-0935-7
Benson D, Bazilevs Y, Hsu M-C, Hughes TJR (2011) A large deformation, rotation-free, isogeometric shell. Comput Methods Appl Mech Eng 200:1367–1378
Sasaki T, Takizawa K, Tezduyar TE (2019) Aorta zero-stress state modeling with T-spline discretization. Comput Mech 63:1315–1331. https://doi.org/10.1007/s00466-018-1651-0
Kuraishi T, Takizawa K, Tezduyar TE (2019) Space-time computational analysis of tire aerodynamics with actual geometry, road contact, tire deformation, road roughness and fluid film. Comput Mech 64:1699–1718. https://doi.org/10.1007/s00466-019-01746-8
Terahara T, Takizawa K, Tezduyar TE, Tsushima A, Shiozaki K (2020) Ventricle-valve-aorta flow analysis with the Space-Time Isogeometric Discretization and Topology Change. Comput Mech 65:1343–1363. https://doi.org/10.1007/s00466-020-01822-4
Takizawa K, Tezduyar TE, Avsar R (2020) A low-distortion mesh moving method based on fiber-reinforced hyperelasticity and optimized zero-stress state. Comput Mech 65:1567–1591. https://doi.org/10.1007/s00466-020-01835-z
Acknowledgements
This work was supported in part by JST-CREST; Grant-in-Aid for Scientific Research (A) 18H04100 from Japan Society for the Promotion of Science; and Rice–Waseda research agreement and International Technology Center Indo-Pacific (ITC IPAC) Contract FA520921C0010. This work was also supported (first author) in part by Pioneering Research Program for a Waseda Open Innovation Ecosystem (W-SPRING). The mathematical model and computational method parts of the work were also supported (fourth author) in part by ARO Grant W911NF-17-1-0046, Contract W911NF-21-C-0030 and Top Global University Project of Waseda University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Dual basis system
The description given here for the relationship between a basis system and its dual is applicable to all the basis systems we work with, where we use the symbols g, \(\overline{g}\), G, and \(\overline{G}\).
For the covariant basis vectors \(\mathbf {g}_\alpha \), the components of the metric tensor are
We define the contravariant basis vectors as
This implies
where the brackets denote the matrix formed from its components, and the contravariant components of the metric tensor are given as
We note that, with \({n_{\mathrm {sd}}}=3\) and \({n_{\mathrm {pd}}}=2\), one of the ways to express the unit tensor is
where
B Derivative and variation of the normal vector in the shell model
1.1 B.1 Derivative of the normal vector
Derivative of the normal vector with respect to \(\xi ^\alpha \) can be obtained as follows:
We note that \(\overline{\kappa }_{\alpha \beta }\) is equal to the second fundamental form with a negative sign. In the derivation, we used the following relationships, which generally hold:
1.2 B.2 Variation of the normal vector
From the steps given by Eqs. (257)–(263), the variation of the normal vector can be written as
1.3 B.3 Rearrangement of the form \(\delta \overline{\mathbf {n}}\cdot \mathbf {h}\)
From Eq. (269), we write
We recall the Lagrange’s identity
With that, we obtain
For notational convenience, we introduce
and
C Integration with variation of the normal vector
1.1 C.1 Dual basis system for the midsurface edges
We have a set of orthonormal basis vectors: \(\overline{\mathbf {B}}\), \(\overline{\mathbf {T}}\), and \(\overline{\mathbf {N}}\). After the deformation:
Here the unit vectors \(\overline{\mathbf {b}}\) and \(\overline{\mathbf {t}}\) may not be orthogonal. To overcome the difficulty of using a set of non-orthogonal basis vectors, we introduced in Remark 17
We repeat them here from Eqs. (138) and (139) for the reader’s convenience. The denominator, a triple scalar product, represents the volume of the parallelepiped based on the three vectors. With that, the counterparts of Eq. (252) can be written as
The counterpart of Eq. (255) is
With the set of basis vectors and stretches, we can express the deformation gradient tensor and its inverse. The deformation gradient tensor can be expressed as
The inverse of \(\overline{\mathbf {F}}\) can be written as
and we have two alternative ways of verifying that. We can show that
by remembering that \(\overline{\mathbf {B}}\), \(\overline{\mathbf {T}}\), and \(\overline{\mathbf {N}}\) are orthonormal and using Eq. (285), or show that
by using Eqs. (281) ,(282), (283) and (284) and remembering that \(\mathbf {I}= \overline{\mathbf {B}}\,\,\overline{\mathbf {B}}+ \overline{\mathbf {T}}\,\,\overline{\mathbf {T}}+ \overline{\mathbf {N}}\,\,\overline{\mathbf {N}}\). By excluding the normal-direction terms in Eqs. (286) and (287), we obtain
Depending on the context, we use either the left- or right-hand side of Eqs. (290) and (291).
We can write \(\mathbf {C}\) at the midsurface as
and its determinant as
where \(\overline{J} = \det \overline{\mathbf {F}}\). Because \(\left( \overline{\mathbf {b}}\times \overline{\mathbf {t}}\right) \cdot \overline{\mathbf {n}}> 0\), we get
We note that, in Eq. (296), the second and third equalities are based on Eqs. (38) and (131), respectively. Thus, Eqs. (279) and (280) can be expressed as
1.2 C.2 Integration over the midsurface
We first rearrange the variation of the normal vector from Eq. (269):
From that, for any vector \(\mathbf {q}\), we have
We integrate the right-hand side of Eq. (302) by parts and obtain
The last integral of the above equation can further be arranged by using the product rule as
Substituting Eq. (265) into this, we obtain
Combining Eqs. (303) and (305) and recognizing the left-hand side of Eq. (291) in the integral over \(\overline{S}_0\), we obtain
1.3 C.3 Integration over the midsurface edges
From Eq. (300), we get
Because of the orthogonality of \(\overline{\mathbf {G}}_\beta \) and \(\overline{\mathbf {N}}\), we obtain
Taking the inner product of \(\overline{\mathbf {g}}_\gamma \) with Eq. (269):
recognizing the right-hand side of that in two places in Eq. (309) and replacing only the second one, we obtain
With that, for any vector \(\mathbf {q}\), we have
We apply integration by parts to the first integral on the right-hand side after recognizing from Eq. (2) that \(\overline{\mathbf {T}}\cdot \overline{\mathbf {G}}^\gamma \delta \overline{\mathbf {g}}_{\gamma } = \overline{\mathbf {T}}\cdot \overline{\mathbf {G}}^\gamma \left( \delta \overline{\mathbf {x}}\right) _{, \gamma }\) and realizing that \(\overline{\mathbf {T}}\cdot \overline{\mathbf {G}}^\gamma \left( \delta \overline{\mathbf {x}}\right) _{, \gamma }\) is the spatial derivative along the line of integration. Keeping in mind that \(\overline{S}_0\) is a closed curve in the integration by parts, we obtain
Using the product rule in the first integral on the right, we get
and by substituting for \(\overline{\mathbf {n}}_{,\gamma }\) from Eq. (265), we obtain
Combining Eqs. (313) and (315) and recognizing the left-hand sides of Eqs. (290) and (291), we obtain
D Constitutive models
We test two constitutive models: neo-Hookean and Fung’s materials. The strain-energy density functions are
where \(\mu \) is the shear modulus, and \(D_1\) and \(D_2 = 8.365\) are the coefficients of the Fung’s material model. The shear modulus at the undeformed configuration is \(\mu _0 = \mu \) for the neo-Hookean material and \(\mu _0 = 2 D_1 D_2\) for the Fung’s material. We determine the bulk modulus from \(\nu \) and \( \mu _0\) as
1.1 D.1 Incompressible material
For incompressible material, we use
and p can be calculated by using the constraint \(J=1\) in the equation associated with the out-of-plane direction. We use the label “\(\nu = 0.5\)” in reporting the results for the incompressible-material cases, but we use the forms above in the tests.
1.2 D.2 Compressible material
For compressible material, we use
where
and we use \(\beta _\mathrm {B} = -2\). This form with \(\beta _\mathrm {B}\) was introduced in [45].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Taniguchi, Y., Takizawa, K., Otoguro, Y. et al. A hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress: I. Out-of-plane deformation. Comput Mech 70, 247–280 (2022). https://doi.org/10.1007/s00466-022-02166-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-022-02166-x