Weakly intrusive time homogenization technique to deal with pseudo-cyclic coupled thermomechanical problems with uncertainties

Abstract

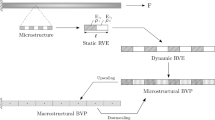
This article is dedicated to the analysis of visco-plastic and damageable structures submitted to thermomechanical loadings embedding some uncertain parameters. In particular, complex time evolutions of the loadings are considered, at two different time scales. An homogenized-in-time model is used to provide kind of a surrogate model for damage evolution analysis. Then a stochastic analysis using polynomial chaos expansion with collocation can be performed. Indeed, though this is a non-intrusive approach, it belongs to the category of many-query problems, so the surrogate model allows to reduce the computational cost in order to be affordable. Focus is herein on the complex time evolutions, the considered test case is mono-dimensional, but up to 300 000 cycles are used.

Appendices

Detailed forms of the state laws and evolution laws

The considered constitutive relations are [33]:

• State laws

  $$\begin{aligned}&\varvec{\sigma }=E\left( 1-D\right) \left( \varvec{\varepsilon }^e-\varpi \theta \varvec{\delta }\right) , \end{aligned}$$

  (27a)
  $$\begin{aligned}&\varvec{\beta }=C\varvec{\alpha }, \end{aligned}$$

  (27b)
  $$\begin{aligned}&R=R_{\infty }\left( 1-\exp \left( -\gamma r\right) \right) , \end{aligned}$$

  (27c)
  $$\begin{aligned}&Y_D=\dfrac{\tilde{\sigma }_{eq}^2 R_v}{2E}. \end{aligned}$$

  (27d)

  $E$ is the Hooke’s tensor which is a function of the modulus of elasticity E and Poisson’s ratio $\nu$. $C$ is a tensor containing material parameter C that describes kinematic hardening. $R_{\infty }$ and $\gamma$ are material parameters describing isotropic hardening. The triaxiality function $R_v=\frac{2}{3}\left( 1+\nu \right) +3\left( 1-2\nu \right) \left( \frac{\sigma _h}{\sigma _{eq}}\right) ^2$, where $\sigma _h=\frac{1}{3}Tr\left( \varvec{\sigma }\right)$ represents the hydrostatic part of the stress tensor, $\sigma _{eq}$ is the von Mises equivalent stress defined as $\sigma _{eq}=\sqrt{\frac{3}{2}\varvec{\sigma }^D:\varvec{\sigma }^D}$ with $\varvec{\sigma }^D=\varvec{\sigma }-\sigma _h\varvec{\delta }$ being the deviatoric stress. The ratio $\frac{\sigma _h}{\sigma _{eq}}$ in the definition of $R_v$ is called the triaxiality ratio and $\tilde{\sigma }_{eq}$ is the equivalent of the effective stress defined as $\tilde{\sigma }_{eq}=\sqrt{\frac{3}{2}\frac{\varvec{\sigma }^D}{\left( 1-D\right) }:\frac{\varvec{\sigma }^D}{\left( 1-D\right) }}$.

• Evolution equations

  $$\begin{aligned}&\dot{ \varvec{\varepsilon }}^p= \dfrac{\partial f^p}{\partial \varvec{\sigma }}\left\langle \dfrac{f_p}{K_v} \right\rangle ^{n_v}, \end{aligned}$$

  (28a)
  $$\begin{aligned}&\dot{\varvec{\alpha }}=-\dfrac{\partial f^p}{\partial \varvec{\beta }}\left\langle \dfrac{f_p}{K_v} \right\rangle ^{n_v}, \end{aligned}$$

  (28b)
  $$\begin{aligned}&\dot{r}= -\dfrac{\partial f^p}{\partial R}\left\langle \dfrac{f_p}{K_v} \right\rangle ^{n_v}, \end{aligned}$$

  (28c)
  $$\begin{aligned}&\dot{D}= \left( \dfrac{Y_D}{S}\right) ^s\dfrac{1}{1-D}\left\langle \dfrac{f_p}{K_v} \right\rangle ^{n_v}, \end{aligned}$$

  (28d)

  with the von Mises yield function $f^p$ delimiting the elastic domain and is defined as

  $$\begin{aligned} f^p= \sqrt{\dfrac{3}{2}\left[ \left( \dfrac{\varvec{\sigma }^D}{1-D}-\varvec{\beta }\right) :\left( \dfrac{\varvec{\sigma }^D}{1-D}-\varvec{\beta }\right) \right] }-R-\sigma _y, \end{aligned}$$

  (29)

  where $\sigma _y$ is the yield stress.The viscous coefficient $K_v$ and viscous exponent $n_v$ are material parameters. The material parameters S and s describe the damage evolution.

Resolution algorithm

The pseudo-code of algorithm 1 is used to solve the two-time-scale problem under concerns. It uses an incremental scheme on the macro time steps, embedding a single Newton-like loop. Inside this last loop, computations are performed on the current micro-time cycle (behind the considered macro time step).