Computational modeling of the large deformation and flow of viscoelastic polymers

Abstract

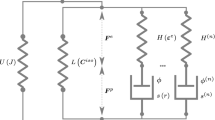
Deformation of soft polymeric materials often involves complex nonlinear or transient mechanical behaviors. This is due to the dynamic behaviors of polymer chains at the molecular level within the polymer network. In this paper, we present a computational formulation to describe the transient behavior (e.g., viscoelasticity) of soft polymer networks with dynamic bonds undergoing large to extreme deformation. This formulation is based on an Eulerian description of kinematics and a theoretical framework that directly connects the molecular-level kinetics of dynamic bonds to the macroscopic mechanical behavior of the material. An extended finite element method is used to discretize the field variables and the governing equations in an axisymmetric domain. In addition to validating the framework, this model is used to study how the chain dynamics affect the macroscopic response of material as they undergo a combination of flow and elasticity. The problems of cavitation rheology and polymer indentation under extreme deformation are investigated in this context.

Appendices

Appendix 1: rate of change in stored elastic energy

To derive the rate of change in elastic energy, we first rewrite Eq. (7) as

$$\begin{aligned} \varDelta \varPsi = \varPsi -\varPsi _0+p\left( \frac{C}{C_0}-1\right) \end{aligned}$$

where $\varPsi = \frac{ck_BT}{2}tr(\varvec{\mu })$ and $\varPsi _0 = \frac{ck_BT}{2}tr(\varvec{\mu }_0)$ are the stored elastic energy at the current and the stress-free state, respectively. Note that for bond exchange reaction, the change of chain concentration is only caused by the change in volume. Therefore, the third term on the right hand side can be equivalently written in terms of volume as $p(\frac{V}{V_0}-1)$. The rate of change in the stored elastic energy is then written as

$$\begin{aligned} \varDelta \dot{\varPsi } = \dot{\varPsi }-\dot{\varPsi }_0+p\;tr(\mathbf {L}) \end{aligned}$$

(38)

where $tr(\mathbf {L})=\mathbf {I}:\mathbf {L}$ is the rate of change in volume. We first evaluate the term corresponding to the current state

$$\begin{aligned} \dot{\varPsi } = \frac{ck_BT}{2}\dot{\varvec{\mu }}:\mathbf {I}. \end{aligned}$$

(39)

We then employ the evolution equation (Eq. (4)) and the above equation becomes

$$\begin{aligned} \dot{\varPsi } = \frac{ck_BT}{2}(2{\varvec{\mu }}:\mathbf {L})-k_d\frac{ck_BT}{2}(\varvec{\mu }-\varvec{\mu }_0). \end{aligned}$$

(40)

Similarly, the term corresponding to the stress-free configuration in Eq. (38) can be obtained as

$$\begin{aligned} \dot{\varPsi }_0 = \frac{ck_BT}{2}(2{\varvec{\mu }_0}:\mathbf {L})-k_d\frac{ck_BT}{2}(\varvec{\mu }_0-\varvec{\mu }_0). \end{aligned}$$

(41)

Combining Eqs. (38), (40) and (41), the rate of change in stored elastic energy reads

$$\begin{aligned} \varDelta \dot{\varPsi }_e=\left[ ck_BT(\varvec{\mu }-\varvec{\mu }_0)+p\mathbf {I}\right] :\mathbf {L}-k_d\frac{ck_BT}{2}tr(\varvec{\mu }-\varvec{\mu }_0). \end{aligned}$$

(42)

Appendix 2: field equations in cylindrical coordinates

In cylindrical coordinates, the balance of momentum equation can be written along the radial and the longitudinal direction as

$$\begin{aligned} \frac{\partial \dot{\sigma }_{\rho \rho }}{\partial \rho }+\frac{1}{r}(\dot{\sigma }_{\rho \rho }-\sigma _{\theta \theta })+\frac{\partial \dot{P}}{\partial \rho }= & {} 0\\ \frac{\partial \dot{\sigma }_{\rho z}}{\partial \rho }+\frac{\partial \dot{\sigma }_{zz}}{\partial z}+\frac{1}{\rho }\dot{\sigma }_{\rho z}+\frac{\partial \dot{P}}{\partial z}= & {} 0. \end{aligned}$$

The condition of incompressibility reads

$$\begin{aligned} \frac{1}{\rho }\frac{\partial }{\partial \rho }(\rho v_\rho )+\frac{\partial v_z}{\partial z}=0. \end{aligned}$$

Appendix 3: discretization of element degrees of freedoms

In the numerical study, XFEM is implemented in the element shape functions to account for the discontinuities. For split elements, the shape function matrices $\mathbf {N_v}$, $\mathbf {N}_{\varvec{\mu }}$, $\mathbf {N_p}$ and the vectors of element nodal values $\mathbf {v}^e$ , $\varvec{\mu }^e$, $\mathbf {p}^e$ contain both standard and enriched DOFs and are defined as

$$\begin{aligned}&\text{ nodal } \text{ DOFs } {\left\{ \begin{array}{ll} \mathbf {v}^e=\left[ \tilde{\mathbf {v}}^{reg};\tilde{\mathbf {v}}^{enr} \right] _{36\times 1},\\ \tilde{\mathbf {v}}^{reg}=\left[ { v}_\rho ^1, { v}_z^1\dots { v}_\rho ^9, { v}_z^9\right] ^T_{18\times r},\\ \tilde{\mathbf {v}}^{enr}=\left[ {\hat{v}}_\rho ^1, {\hat{v}}_z^1\dots {\hat{v}}_\rho ^9, {\hat{v}}_z^9\right] ^T_{18\times 1};\\ \varvec{\mu }^e=\left[ \tilde{\varvec{\mu }}^{reg};\tilde{\varvec{\mu }}^{enr} \right] _{40\times 1},\\ \dot{\mathbf {p}}^e=\left[ \tilde{\dot{\mathbf {p}}}^{reg};\tilde{\dot{\mathbf {p}}}^{enr} \right] _{8\times 1},\\ \tilde{\dot{\mathbf {p}}}^{reg}=\left[ {\dot{p}}^1, \dots , {\dot{p}}^4 \right] ^T_{4\times r},\\ \tilde{\dot{\mathbf {{p}}}}^{enr}=\left[ \hat{{\dot{p}}}^1, \dots , \hat{{\dot{p}}}^4\right] ^T_{4\times 1};\\ \end{array}\right. }\\&\text{ shape } \text{ functions } {\left\{ \begin{array}{ll} \mathbf {N_v}=\left[ \mathbf {N}_{\mathbf {v}}^{reg};\mathbf {N}_{\mathbf {v}}^{enr} \right] _{2\times 36},\\ \mathbf {N_p}=\left[ \mathbf {N}_{\mathbf {p}}^{reg};\mathbf {N}_{\mathbf {p}}^{enr} \right] _{1\times 8},\\ \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \mathbf {N}_{\mathbf {v}}^{reg}= & {} \left[ \mathbf {N}_{\mathbf {v}}^{1},\dots ,\mathbf {N}_{\mathbf {v}}^{9} \right] _{2\times 18},\nonumber \\ \mathbf {N}_{\mathbf {v}}^{enr}= & {} \left[ \mathcal {S}^1\mathbf {N}_{\mathbf {v}}^{1},\dots ,\mathcal {S}^9\mathbf {N}_{\mathbf {v}}^{9} \right] _{2\times 18} \end{aligned}$$

(43)

$$\begin{aligned} \mathbf {N}_{\mathbf {p}}^{reg}= & {} \left[ N_4^{1},\dots ,N_4^{4} \right] _{1\times 4},\nonumber \\ \mathbf {N}_{\mathbf {p}}^{enr}= & {} \left[ \mathcal {S}^1N_4^{1},\dots ,\mathcal {S}^4 N_4^4 \right] _{1\times 4} \end{aligned}$$

(44)

and $\mathbf {N_v}^I=\begin{bmatrix} N_9^I&0 \\ 0&N_9^I \end{bmatrix}.$

Here, we note that $\mathcal {S}^I=H(\phi (\mathbf {x})-H(\phi (\mathbf {x}^I))$. To compute the deformation rate of the material, velocity gradient tensor and the divergence of velocity are written as

$$\begin{aligned} \mathbf {D}=(\varvec{\nabla }\mathbf {v})^s=\mathbf {B_v}\cdot \mathbf {v}^e\quad \text{ and }\quad \varvec{\nabla }\cdot \mathbf {v} =\hat{\mathbf {B}}_\mathbf {v}\cdot \mathbf {v}^e. \end{aligned}$$

The rate $\mathbf {B_v}$ and $\hat{\mathbf {B}}_\mathbf {v}$ matrices that are related to the nodal velocities to deformation rates are written in the cylindrical coordinates as

$$\begin{aligned} \mathbf {B_v}= & {} \left[ \mathbf {B_v}^1,\dots ,\mathbf {B_v}^9,\mathcal {S}^1\mathbf {B_v}^1,\dots ,\mathcal {S}^9\mathbf {B_v}^9 \right] _{4\times 36}\\ \text{ with }\; \; \mathbf {B_v}^I= & {} \begin{bmatrix} \frac{\partial N_9^I}{\partial \rho }&0 \\ 0&\frac{\partial N_9^I}{\partial z}\\ \frac{\partial N_9^I}{\partial z}&0 \\ 0&\frac{\partial N_9^I}{\partial \rho } \\ \frac{N_9^I}{\rho }&0 \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned}&\hat{\mathbf {B}}_\mathbf {v}=\left[ \hat{\mathbf {B}}_\mathbf {v}^1,\dots ,\hat{\mathbf {B}}_\mathbf {v}^9,\mathcal {S}^1\hat{\mathbf {B}}_\mathbf {v}^1,\dots ,\mathcal {S}^9\hat{\mathbf {B}}_\mathbf {v}^9 \right] _{4\times 36} \end{aligned}$$

(45)

$$\begin{aligned}&\text{ with }\; \; \hat{\mathbf {B}}_\mathbf {v}^I =\begin{bmatrix} \frac{\partial N_9^I}{\partial \rho }+ \frac{N_9^I}{\rho }&\frac{\partial N_9^I}{\partial z} \end{bmatrix}. \end{aligned}$$

(46)

Appendix 4: element tangent matrix for governing equations

Using the equations of the evolution of the distribution tensor $\varvec{\mu }$ (3), the components of the tangent matrix corresponding to the linear system (19) can be obtained as

$$\begin{aligned} \mathbf {K_{vv}}= & {} ck_BT\int _{\varOmega ^e}\mathbf {B}^T_{\mathbf {v}}\cdot \tilde{\varvec{\mu }}\cdot \mathbf {B_v}\; d\varOmega ^e \nonumber \\ \mathbf {K_{vp}}= & {} \int _{\varOmega ^e}\mathbf {B}^T_{\mathbf {v}}\cdot \mathbf {N_p}\; d\varOmega ^e \nonumber \\ \mathbf {K_{vp}}= & {} \int _{\varOmega ^e}\mathbf {N}^T_{\mathbf {p}}\cdot \hat{\mathbf {B}}_{\mathbf {v}}\; d\varOmega ^e\nonumber \\ \mathbf {K_{v\lambda }}= & {} \int _{\varGamma ^e}\mathbf {N}^T_v\cdot \mathbf {N}_\lambda \; d\varGamma ^e \nonumber \\ \mathbf {K_{\lambda v}}= & {} \int _{\varGamma ^e}\mathbf {N}_\lambda ^T\cdot \mathbf {N}_v\; d\varGamma ^e \end{aligned}$$

(47)

and the element residual tensors

$$\begin{aligned} \mathbf {f}_v= & {} \int _{\varOmega ^e} \mathbf {B}^T_{\mathbf {v}}\cdot \left[ k_a\frac{C-\tilde{c}}{\tilde{c}}\mathbf {I}+k_d\varvec{\mu }\right] \;d\varOmega ^e\; + \int _{\varGamma ^e} \mathbf {N}^T_{\mathbf {v}}\cdot \dot{\overline{\varvec{t}}}\;d\varGamma ^e\nonumber \\&+\int _{\varOmega ^e} \mathbf {N}^T_{\mathbf {v}}\cdot \dot{\mathbf {b}}\;d\varOmega ^e\nonumber \\ \mathbf {f}_\lambda= & {} \int _{\varOmega ^e} \bar{\mathbf {N}}^T\cdot \bar{\mathbf {v}}\;d\varGamma ^e. \end{aligned}$$

(48)

Here, we write the distribution tensor $\varvec{\mu }=[\mu _{\rho \rho },\;\mu _{zz},\;$$\mu _{\rho z},\;\mu _{z\rho },\;\mu _{\theta \theta } ]$ in Voigt notation. Accordingly, $\tilde{\varvec{\mu }}$ is the distribution tensor $\varvec{\mu }$ written in the Mandel form and the components in $\tilde{\varvec{\mu }}$ read

$$\begin{aligned} \tilde{\varvec{\mu }}=\begin{bmatrix} 2\tilde{\mu }_{\rho \rho }&0&2\tilde{\mu }_{z\rho }&0&0\\ 0&2\tilde{\mu }_{zz}&0&2\tilde{\mu }_{\rho z}&0\\ \tilde{\mu }_{\rho z}&\tilde{\mu }_{z\rho }&\tilde{\mu }_{zz}&\tilde{\mu }_{\rho \rho }&0\\ \tilde{\mu }_{\rho z}&\tilde{\mu }_{z\rho }&\tilde{\mu }_{zz}&\tilde{\mu }_{\rho \rho }&0\\ 0&0&0&0&\tilde{\mu }_{\theta \theta }\\ \end{bmatrix}. \end{aligned}$$

(49)

In the above equations, the variables with tilde superscript $\tilde{(.)}$ indicate that they are interpolated using the fields from the previous timestep. We note that in many problems, the values of boundary traction $\overline{\varvec{t}}$ and body force $\mathbf {b}$ are usually given instead of their time derivatives $\dot{\overline{\varvec{t}}}$ and $\dot{\mathbf {b}}$. In this case, a forward difference scheme is used for the time derivatives. For example, at time step n

$$\begin{aligned} \dot{\overline{\varvec{t}}}_{n}(\mathbf {x})= & {} \frac{\overline{\varvec{t}}_{n+1}(\mathbf {x})-\bar{\varvec{t}}_{n}(\mathbf {x})}{\varDelta t}\nonumber \\ \dot{\varvec{b}}_{n}(\mathbf {x})= & {} \frac{\varvec{b}_{n+1}(\mathbf {x})-\varvec{b}_{n}(\mathbf {x})}{\varDelta t}. \end{aligned}$$

(50)

Appendix 5: evolution of the interface

As discussed in the text, the interface is characterized and tracked using the PMIM algorithm with the following steps:

(a) Interface initialization At the initial time $t_0$, the interface is discretized by the particles, whose position vector $\mathbf {y}$ are chosen as the closest points from each neighboring grid nodes to the interface. The position vector $\mathbf {y}$ can be obtained using our knowledge of initial levelset function $\phi (\mathbf {x}, t_0)$ as

$$\begin{aligned} \mathbf {y}=\mathbf {x}-\phi (\mathbf {x}, t_0)\bar{\mathbf {n}}(\mathbf {x}, t_0) \end{aligned}$$

(51)

where the normal vector is obtained by $\bar{\mathbf {n}}=\nabla \phi (\mathbf {x}, t_0)$ [27] and $\mathbf {x}$ is the position vector of the corresponding grid node.

(b) Update the interface At an arbitrary time t, given the velocity solution of the interface velocity $\bar{\mathbf {v}}^t$, update the position of each particle by a second order Runge-Kutta scheme as

$$\begin{aligned} \mathbf {y}^{t+\frac{dt}{2}}= & {} \mathbf {y}^t+\bar{\mathbf {v}}(\mathbf {y}^t,\;t)\frac{dt}{2}+\varvec{\varOmega }\cdot \bar{\mathbf {v}}(\mathbf {y}^t,\;t)\frac{dt^2}{4}\nonumber \\ \mathbf {y}^{t+dt}= & {} \mathbf {y}^t+\bar{\mathbf {v}}(\mathbf {y}^{t+\frac{dt}{2}},\;t)\frac{dt}{2}+\varvec{\varOmega }\cdot \bar{\mathbf {v}}(\mathbf {y}^{t+\frac{dt}{2}},\;t)\frac{dt^2}{2} \end{aligned}$$

(52)

where $\varvec{\varOmega }$ is the skew-symmetric spin tensor that reads

$$\begin{aligned} \varvec{\varOmega }=\begin{bmatrix} 0&-\omega _z\\ \omega _z&0]\end{bmatrix}\quad \text{ with }\quad \varvec{\omega }_z=(\bar{v}_{,\xi ^2}^\parallel -\bar{v}_{,\xi ^1}^\parallel ). \end{aligned}$$

(53)

The function is then updated to account for the new geometry of the interface

$$\begin{aligned} \phi (\mathbf {y},\;t+dt)=g(\mathbf {y}^{t+dt},\;\mathbf {x})|\mathbf {y}^{t+dt}-\mathbf {x}| \end{aligned}$$

(54)

where $g(\mathbf {y}^{t+dt},\;\mathbf {x})$ is a sign function that determines whether a point $\mathbf {x}$ locates inside or outside of the interface

$$\begin{aligned} g(\mathbf {y}^{t+dt},\;\mathbf {x})=-sgn\left( \frac{\mathbf {y}^{t+dt}-\mathbf {x}}{|\mathbf {y}^{t+dt}-\mathbf {x}|}\cdot \bar{\mathbf {n}}^t\right) . \end{aligned}$$

(55)

It is clear that the function g takes the value $-\,1$ inside the vesicle, and 1 outside the vesicle.

(c) Interface approximation After obtaining the updated levelset function, the interface geometry is approximated using the local polynomials for each particle P. More specifically, for each particle P with position vector $\mathbf {y}_p$, one can introduce a local orthonormal basis that consists of tangent and normal vectors $\{\bar{\mathbf {a}}^{t+dt}_p, \bar{\mathbf {n}}^{t+dt}_p\}$ to the interface. These two quantities can be obtained from the levelset function as follows

$$\begin{aligned} \bar{\mathbf {n}}^{t+dt}_p= & {} \nabla \phi (\mathbf {y}_p,\;t+dt)\nonumber \\ \bar{\mathbf {a}}^{t+dt}_p= & {} \bar{\mathbf {n}}^{t+dt}_p\times \mathbf {m}/|\bar{\mathbf {n}}^{t+dt}_p\times \mathbf {m}| \end{aligned}$$

(56)

where $\mathbf {m}=[0\;0\;1]^T$ is the unit vector normal to the computational domain. To approximate the local geometry of the interface, we collect the closest m particles in the neighborhood of P, given by their positions $\tilde{\mathbf {y}}_1\dots \tilde{\mathbf {y}}_m$ in the local coordinates

$$\begin{aligned} \tilde{\mathbf {y}}_i=\left\{ \begin{array}{c}\xi _i^1\\ \xi _i^2\end{array}\right\} =\mathbf {R}^{t+dt}\cdot (\mathbf {y}_i-\mathbf {y}_p)\quad \text{ with }\quad \mathbf {R}^{t+dt}= \begin{bmatrix}\bar{\mathbf {a}}^{t+dt}_p\\ \bar{\mathbf {n}}^{t+dt}_p\\ \end{bmatrix} \end{aligned}$$

(57)

and construct a polynomial using the least square fitting method

$$\begin{aligned} \xi ^2(\xi ^1)=\sum _{i=0}^n c_i(\xi ^1)^i \end{aligned}$$

(58)

where the coefficients $c_i$ are determined by minimizing the $L^2$ difference between the approximation $\xi ^2(\xi _i^1)$ and the nodal values $\xi _i^2$. In this way, a local parameterization $\mathbf {r}^l(\rho ,\;t)$ of the interface around the particle $\mathbf {y}_p$ is achieved, whose global parameterization $\mathbf {r}(\rho ,\;t)$ can then be obtained as

$$\begin{aligned} \mathbf {r}(\rho ,\;t)=(\mathbf {R}^{t+dt})^{-1}\mathbf {r}^l(\xi ^1,\;t)+\mathbf {y}_p. \end{aligned}$$

(59)

Finally, the tangential and normal vectors for a point on the interface $\varGamma$ can be obtained in the global coordinates as

$$\begin{aligned} \bar{\mathbf {a}}^{t+dt}= & {} \mathbf {r}(\rho ,\;t+d)_{,\rho }=\mathbf {R}^{t+dt}\frac{\partial \mathbf {r}^l(\xi ^1,\;t)}{\partial \xi ^1}\nonumber \\ \bar{\mathbf {n}}^{t+dt}= & {} \bar{\mathbf {a}}^{t+dt}\times \mathbf {m}/|\bar{\mathbf {a}}^{t+dt}\times \mathbf {m}|. \end{aligned}$$

(60)

Appendix 6: element matrices for enriched degrees of freedom

The global tangent matrices to compute the enriched degrees of freedom $\overline{\varvec{\mu }}^{enr}_g$ and $\overline{\mathbf {p}}^{enr}_g$ are written as

$$\begin{aligned} \mathbf {K}_{\varvec{\mu }}^{enr}= & {} \sum _e\int _{\varOmega ^e}(\mathbf {N}_{\varvec{\mu }}^{enr})^T\mathbf {N}_{\varvec{\mu }}^{enr}d\varOmega ^e\end{aligned}$$

(61)

$$\begin{aligned} \mathbf {K}_{\mathbf {p}}^{enr}= & {} \sum _e\int _{\varOmega ^e}(\mathbf {N}_{\mathbf {p}}^{enr})^T\mathbf {N}_{\mathbf {p}}^{enr}d\varOmega ^e \end{aligned}$$

(62)

and the residue vector is given by

$$\begin{aligned} \mathbf {R}_{\varvec{\mu }}^{enr}= & {} \sum _e\int _{\varOmega ^e}(\mathbf {N}_{\varvec{\mu }}^{enr})^T\left( \tilde{\varvec{\mu }}-\mathbf {N}_{\varvec{\mu }}^{reg}\varvec{\mu }^{reg}\right) d\varOmega ^e\nonumber \\ \mathbf {R}_{\mathbf {p}}^{enr}= & {} \sum _e\int _{\varOmega ^e}(\mathbf {N}_{\mathbf {p}}^{enr})^T\left( \tilde{\mathbf {p}}-\mathbf {N}_{\mathbf {p}}^{reg}\mathbf {p}^{reg}\right) d\varOmega ^e. \end{aligned}$$

(63)

In the above equations $\sum _e$ indicates the matrix assembly of the global system from the element matrices.