Abstract
A theoretical and computational framework for the analysis of thermomechanically coupled transient rolling contact, based on an arbitrary Lagrangian–Eulerian (ALE) kinematical description, is developed. A finite element formulation featuring 2D cylinder–plate rolling contact is implemented. The implementation features penalty-type contact formulations for mechanical and thermal contact. It is noted that the ALE formulation allows for a simplified time description, a compact computational domain and localized mesh refinement. Numerical simulations considering stationary and transient rolling conditions are presented. Highlighted aspects include the influence of variations in thermal contact conductivity, rolling speed and external mechanical load on the contact interface heat flow. The model is shown to give predictions in qualitative agreement with results in the literature. For the velocity range studied, numerical issues such as spurious numerical dissipation/oscillations in the temperature field are noted to have a prominent influence. These phenomena are addressed using a Streamline-Upwind Petrov–Galerkin stabilization scheme together with a bubble function approach.
Similar content being viewed by others
1 Introduction
Thermomechanical analysis of bodies in rolling contact is of significant engineering and theoretical interest. Thermal expansion, dissipative heat generation and frictional heat generation [1] are all modes of thermomechanical coupling which may significantly influence the mechanical and thermal behaviour of the contacting bodies, as well as their material properties. Examples of applications where a thermomechanical analysis might be crucial for an accurate description of the response include rolling mills, roller bearings and wheel–rail contacts [2]. It should here be noted that the flow of heat through the contact interface (in railway applications denoted “rail chill”), as well as the partitioning of the frictional heat generated at the contact interface, depend strongly on the rolling velocity [3, 4]. This point will be further discussed in subsequent sections.
A common approach to numerical modelling of rolling contact is to employ a semi-analytical contact model based on Hertz theory [5–7]. Such an implementation is simple and fast, but limited by assumptions of elastic material response, smooth, continuous surfaces and a small relative dimension of the contact patch. In contrast, a contact formulation involving deformation dependent contact forces and an iterative contact search algorithm [7, 8] adds a significant (often much-needed) versatility. However, this approach is relatively complicated to implement and increases computational demands.
In finite element modelling of solid mechanics problems, a Lagrangian kinematical description is usually employed. When modelling rolling contact in particular, a problem formulation based instead on an arbitrary Lagrangian–Eulerian (ALE) description provides important advantages [8, 9]. These (elaborated in following sections) include the possibility to linearize the mechanical response, the compactness of the computational domain, the simplified time description, the possibility for highly localized mesh refinement and the elimination of the need for velocity-dependent contact conductivity modelling.
The mathematical foundations of mechanical rolling contact in the context of an ALE description were first presented in Nackenhorst [9]. Here, the relevant kinematical description, balance laws, weak forms and contact kinematics are discussed in elaborate detail. The paper highlights the advantages of the ALE approach, but also discusses complications stemming from the intrinsic difficulty of tracing material points in this case. These include the difficulty of handling inelastic material behaviour as well as keeping track of relative slip distances. Both of these issues were addressed in Ziefle and Nackenhorst [10], where a staggered solution scheme is suggested, i.a. involving solution of the advection equation to keep track of internal variable data. In a recent paper [11], the use of an ALE method for thermomechanically coupled stationary rolling contact is introduced. Here, a thermoviscoelastic constitutive model is employed, involving large deformations and temperature-dependent constitutive parameters.
The present paper aims to provide a comprehensive presentation of thermomechanically coupled transient rolling contact in the context of an ALE description. Specific attention is here given to the stress, the deformation-induced heat source, the heat flux and the mechanical and thermal boundary conditions as they appear in the ALE framework. Furthermore, issues of numerical inaccuracy related to the solution of the discretized energy balance equation are discussed in detail, and stabilization measures are suggested.
The paper is outlined as follows: In Sect. 2, the kinematical description of the rolling cylinder on the plate is presented. The thermomechanical boundary value problem, including its finite element formulation, is defined in Sect. 3. Section 4 contains a discussion about element choice and numerical stabilization measures necessary for an accurate numerical response. In Sect. 5, the mechanical and thermal contact formulations are described. Numerical examples are presented in Sect. 6. In particular, the model is validated and the influence of key operational parameters is evaluated. With Sect. 7, the paper is concluded with a summary and an outlook towards future work.
2 ALE description of rolling contact
The employed ALE description of cylinder–plate rolling motion [12] can be described as follows: Two intermediate configurations are utilized in addition to the initial (“undeformed”) configuration, \(\varOmega \ni \varvec{X}\), and the current (“deformed”) configuration, \(\omega \ni \varvec{x}\). The first intermediate configuration is denoted \(\hat{\varOmega }\ni \varvec{\hat{X}}\). The map from \(\varOmega \) to \(\hat{\varOmega }\) accounts for a rigid body rotation of the cylinder and a pure translation of the plate. The second intermediate configuration is denoted \(\hat{\omega }\ni \varvec{\hat{x}}\). The map from \(\hat{\varOmega }\) to \(\hat{\omega }\) accounts for the deformation of cylinder and plate. Both intermediate configurations feature a moving coordinate system that follows the cylinder centre. The map from \(\hat{\omega }\) to \(\omega \) accounts for a pure translation of the system in going back to the original fixed coordinate system.
The maps between the configurations are formulated as \(\varvec{\hat{X}}=\varvec{\hat{\phi }}(\varvec{X},t)\), \(\varvec{\hat{x}}=\varvec{\hat{\varphi }}(\varvec{\hat{X}},t)\), \(\varvec{x}=\varvec{\check{\phi }}(\varvec{\hat{x}},t)\) and \(\varvec{x}=\varvec{\varphi }(\varvec{X},t)\), so that \(\varvec{\varphi }(\varvec{X}, t)=\varvec{\check{\phi }}(\varvec{\hat{\varphi }}(\varvec{\hat{\phi }}(\varvec{X}, t), t), t)\). The corresponding deformation gradients are, in respective order: \(\varvec{\hat{f}}\), \(\varvec{\hat{F}}\), \(\varvec{\check{f}}\) and \(\varvec{F}\). Figure 1 shows a schematic illustration of the employed configurations, with their intermediary maps and deformation gradients.
Illustration of configurations and maps relevant to the employed ALE description
The rigid body maps \(\varvec{\hat{X}}=\varvec{\hat{\phi }}(\varvec{X},t)\) and \(\varvec{x}=\varvec{\check{\phi }}(\varvec{\hat{x}},t)\) can be expressed a priori from knowledge of the translational and rotational motion of the cylinder along the plate:
where \(\varvec{R}\) is a rotation tensor, \(\varvec{X}_0\) is the position of the cylinder centre in the undeformed configuration, \(\varvec{\bar{X}}\) is the translation of the cylinder centre and \(\varOmega ^{\mathrm{c}}\) and \(\varOmega ^{\mathrm{p}}\) are the subsets of \(\varOmega \) representing the cylinder and plate domains, respectively. Note that \(\varvec{\hat{f}}=\varvec{R}\) and \(\varvec{\hat{f}}=\varvec{I}\) in the domain of the cylinder and plate, respectively, and that \(\varvec{\check{f}}=\varvec{I}\). The Lagrangian problem of finding the map \(\varvec{x}=\varvec{\varphi }(\varvec{X},t)\) (or the displacement \(\varvec{u}(\varvec{X},t)=\varvec{\varphi }(\varvec{X},t)-\varvec{X}\)) is thus narrowed down to the ALE problem of finding the map \(\varvec{\hat{x}}=\varvec{\hat{\varphi }}(\varvec{\hat{X}},t)\) (or the displacement \(\varvec{\hat{u}}(\varvec{\hat{X}},t)=\varvec{\hat{\varphi }}(\varvec{\hat{X}},t)-\varvec{\hat{X}}\)). For small strains, the ALE displacements \(\varvec{\hat{u}}\) will be small, which is generally not the case for the standard Lagrangian displacements \(\varvec{u}\). Consequently, in the former case (but not the latter) it is possible to linearize the mechanical response. In particular, it is noted that the total deformation gradient can be expressed as
since \(\varvec{\check{f}}=\varvec{I}\). The linearization of the material behaviour pertains to the assumption that \(\varvec{\hat{F}}\approx \varvec{I}\) while \(\varvec{\hat{f}}\) is arbitrary. This point is elaborated in Sect. 3.
Another advantage of the presented convective kinematical description is the fact that it allows for a compact computational model: only a relatively short section of the plate domain needs to be modelled, regardless of rolling distance. Further, the position (in the intermediate domains) of the contact region in both cylinder and plate is largely stationary throughout the rolling motion, allowing for localized mesh refinement. Figure 10 in Sect. 6 illustrates these points.
A potential difficulty in convective formulations is the tracking of boundaries. In the present case, since a round cylinder and a flat plate are considered, the boundaries are stationary and this is not a problem. However, numerical problems due to convective effects will require attention (see Sect. 4).
3 Thermomechanical problem
In the following, the strong and weak forms as well as the finite element formulation of the thermomechanically coupled problem are derived in terms of the ALE description. Isotropic, homogeneous and thermoelastic materials are initially assumed. Plane strain and linear elasticity are later assumed in the derivation of the FE formulation.
3.1 Strong form
The local balance of momentum equation with respect to a volume element in the initial configuration \(\varOmega \) is
where \(\varvec{P}= \varvec{P}(\varvec{F}, \theta )\) is the first Piola–Kirchhoff stress tensor, \(\rho \) is the density in the initial configuration, \(\varvec{B}\) is the external body force per unit volume (in the initial configuration) and \(\varvec{a}\) is the acceleration: \(\varvec{a} = D_{tt}\varvec{x} = D_{tt}\varvec{u}\), where \(\left. D_t(\cdot ) :=\partial (\cdot )/\partial t\right| _{\varvec{X}}\) Footnote 1, \(\left. D_{tt}(\cdot ) :=\partial ^2(\cdot )/\partial t^2\right| _{\varvec{X}}\). \(\varvec{\nabla }_X\) is the vector differential operator with respect to \(\varOmega \). Boundary conditions are imposed as \((\varGamma :=\partial \varOmega )\)
where \(\varvec{T} :=\varvec{P}\cdot \varvec{N}\) (\(\varvec{N}\) is the outward normal), \(\varvec{T}_\mathrm{P}\) is the prescribed external traction per unit area with respect to \(\varOmega \) and \(\varvec{u}_\mathrm{P}\) represents prescribed displacements.
In terms of the ALE description, the momentum balance equation takes the formFootnote 2 [12]
where \(d_t(\cdot ):=\partial (\cdot )/\partial t|_{\varvec{\hat{X}}}\), \(d_{tt}(\cdot ):=\partial ^2(\cdot )/\partial t^2|_{\varvec{\hat{X}}}\) are referential time derivatives, \(\varvec{\hat{F}}:=\varvec{\hat{x}}\otimes \varvec{\hat{\nabla }}\), \(\varvec{\hat{G}}:=\varvec{\hat{x}}\otimes \varvec{\hat{\nabla }}\otimes \varvec{\hat{\nabla }}\), and
is the convective velocity pertinent to the map \(\varvec{\hat{\phi }}\) (see Eq. (1)). Note that due to the nature of the rotation tensor, \(\varvec{\hat{\nabla }}\cdot \varvec{\bar{v}}= 0\). \(\hat{(\cdot )}\) denotes quantities related to \(\hat{\varOmega }\). In particular, \(\varvec{\hat{P}}=\varvec{P}\cdot \varvec{\hat{f}}^{\mathrm {T}}\) is the push-forward of the first Piola–Kirchhoff stress tensor to \(\hat{\varOmega }\).
For a thermoelastic material, the constitutive relation \(\varvec{P}(\varvec{F}, \theta )\) for the first Piola–Kirchhoff stress can be defined from a free energy function \(\varPsi (\varvec{F}, \theta )\) such that \(\varvec{P}(\varvec{F}, \theta )=\partial \varPsi (\varvec{F}, \theta )/\partial \varvec{F}\). For an isotropic material, \(\varPsi \) should be independent of any rotation prior to the deformation, i.e.
for an arbitrary deformation gradient \(\varvec{F}\), temperature \(\theta \) and rotation tensor \(\varvec{R}\). Consequently, the derivatives of \(\varPsi \) with respect to \(\varvec{F}\) (i.e. the stress) must satisfy the conditions
for any \(\varvec{\tilde{F}}\) and any \(\varvec{R}\). As a consequence,
for any \(\varvec{\hat{f}}\) being either a rotation (as in the cylinder) or the identity (as in the plate). Hence, the original constitutive model can be used and \(\varvec{\hat{P}}\) \(( = \varvec{\hat{P}}(\varvec{\hat{F}}, \theta ) = \varvec{P}(\varvec{F}, \theta )\cdot \varvec{\hat{f}}^{\mathrm {T}}= \varvec{P}(\varvec{\hat{F}}\cdot \varvec{\hat{f}}, \theta )\cdot \varvec{\hat{f}}^{\mathrm {T}}= \varvec{P}(\varvec{\hat{F}}, \theta ))\) can be expressed independently of \(\varvec{\hat{f}}\). For small deformation/temperature thermoelasticity (\(\varvec{F}\approx \varvec{I}\) and \(\theta \approx \theta ^{\mathrm{ref}}\)) it is commonly adopted that \(\varvec{P}\approx \varvec{\mathsf {E}}\mathbin {:}[\varvec{H}- \alpha \bar{\theta }\varvec{I}]\), where \(\varvec{H}=\varvec{F}-\varvec{I}\), \(\varvec{\mathsf {E}}\) is the elasticity tensor, \(\alpha \) is the thermal expansion coefficient and \(\bar{\theta }= \theta - \theta ^{\mathrm{ref}}\) is the excess temperature with respect to the reference \(\theta ^{\mathrm{ref}}\). Therefore, the linearization of \(\varvec{\hat{P}}\) for small strains (\(\varvec{\hat{F}}\approx \varvec{I}\)) and small temperature fluctuations (\(\theta \approx \theta ^{\mathrm{ref}}\)), becomes
where \(\varvec{\hat{H}}=\varvec{\hat{F}}-\varvec{I}\) and \(K\) is the bulk modulus. Hence, for an unconstrained specimen (\(\varvec{\hat{P}}= 0\)), the temperature driven deformation is \(\varvec{\hat{F}}= (1 + \alpha \bar{\theta })\varvec{I}\).
Remark 1
In the cylinder domain, it is only the relation \(\varvec{\hat{P}}(\varvec{\hat{F}})\) —and not \(\varvec{P}(\varvec{F})\) — that can be linearized, since \(\varvec{F}\) will here contain a finite rotation (see Eqs. (3) and (1)).
The boundary conditions can in the ALE framework be phrased as
where \(\varvec{\hat{T}}^{\mathrm{TOT}}\) in the Robin-type boundary condition (12a) is the natural boundary traction obtained via integration by parts in the weak form (see Sect. 3.2).
The strong form of the energy balance equation with respect to the initial configuration \(\varOmega \) is [13, 14]
where
is the deformation-induced heat source, \(c\) is the mass specific heat capacity, \(\varvec{q}\) is the heat flux and \(r\) is the external heat power per unit volume (in the initial configuration). Boundary conditions are imposed as
where \(q_N :=\varvec{q}\cdot \varvec{N}\). In terms of the ALE description, the energy balance equation takes the form
where \(\hat{(\cdot )}\) denotes quantities related to \(\hat{\varOmega }\). In particular, \({\hat{\beta }}={\beta }\cdot \varvec{\hat{f}}^{\mathrm {T}}\) and \(\varvec{\hat{q}}=\varvec{\hat{f}}\cdot \varvec{q}\) were introduced. Furthermore, for isotropic materials,
where Eq. (10) was used and a known constitutive relation \({\beta }(\varvec{F}, \theta )\) in the initial configuration was assumed. Hence,
where the last equality is valid for the linearized case (see Eq. (11)).
Furthermore, in analogy with the result for the first Piola–Kirchhoff stress, it can be shown that for an isotropic material (and for \(\varvec{\hat{f}}\) being a rotation or the identity tensor),
where it was tacitly assumed that the heat flux only depends on the gradient of the temperature with respect to the initial configuration. In particular, the linear Fourier’s law is henceforth adopted, whereby it is obtained that
where \(k\) is the constant heat conductivity.
The boundary conditions can in the ALE framework be phrased as
where \(\hat{q}^{\mathrm{TOT}}_{\hat{N}}\) in the Robin-type boundary condition (21a) is the natural boundary flux obtained via integration by parts in the weak form (see Sect. 3.2).
Linearizing the energy balance Eq. (16) for small strains and small temperature fluctuations gives
For isotropic materials, (18) is valid, and we obtain
where it was used that \(\varvec{\bar{v}}\) is divergence free (see Eq. (7)).
In summary: For homogeneous, isotropic materials, the residuals of the linearized strong form of the transient thermomechanically coupled problem are
where the linearized form of \(\varvec{\hat{P}}\) is given in (11). It is clear from (11) that \(\varvec{\hat{P}}\) is temperature dependent, due to the influence of thermal expansion. This constitutes the influence of the temperature field on the momentum balance equation. Furthermore, the deformation-dependent terms in the second equation above represents the Gough–Joule effect: reversible heating/cooling of the material resulting from a nonzero strain rate [15]. In the ALE context, this term is split into a referential derivative and a convective term (as seen above). In a stationary analysis, the former vanishes. It should be noted that the Gough–Joule effect is negligible for thermoelastic materials [13]. Consequently, the thermomechanical coupling is one-sided in this case.
It can be seen that when the translational and rotational velocity of the system is constant in time, \(\varvec{\bar{v}}\) and \(\varvec{\ddot{\bar{X}}}\) are constant in time (specifically, \(\varvec{\ddot{\bar{X}}}= 0\)) and the time dependence in the above equations is confined to the solution fields (and the external loads).
If stationary rolling conditions are assumed, all referential time derivatives (\(d_t\), \(d_{tt}\)) as well as \(\varvec{\ddot{\bar{X}}}\) are zero, resulting in a time-independent problem involving the residuals
3.2 Weak form
The weak form is obtained by weighting the local expressions in Eq. (24) with arbitrary (time-independent) test functions \((\delta \varvec{\hat{u}}, \delta \bar{\theta })\in \varvec{\mathcal {V}}_u^0\times \mathcal {V}_\theta ^0\), integrating over the whole domain \(\hat{\varOmega }\) and performing integration by parts. The weak residuals are thus defined as
where
where
and it was used that
Remark 2
As shown in Nackenhorst [9], it is possible to obtain a higher degree of symmetry in the weak form (26) by partial integration of the second term on the right-hand side:
where the divergence theorem and the fact that \(\varvec{\bar{v}}\) is divergence free were used. It is noted that the first two terms on the right-hand side constitute an antisymmetric contribution to the weak form.
The term \(\varvec{\hat{T}}^{\mathrm{TOT}}\) emerges from the ALE formulation of the momentum balance equation. Thus, prescribing \(\varvec{\hat{T}}^{\mathrm{TOT}}\) on \(\hat{\varGamma }_{\mathrm{N}_u}\) constitutes a natural (Neumann) boundary condition:
If instead the intrinsic (physical) traction \(\varvec{\hat{T}}:=\varvec{\hat{P}}\cdot \varvec{\hat{N}}\) is prescribed, a Robin-type boundary condition is obtained:
where the boundary \(\hat{\varGamma }_{\mathrm{N}_u}\) was simply renamed \(\hat{\varGamma }_{\mathrm{R}_u}\) in order to reflect the type of boundary condition in effect. Similarly, prescribing the quantity \(\hat{q}^{\mathrm{TOT}}_{\hat{N}}\) on \(\hat{\varGamma }_{\mathrm{N}_\theta }\) constitutes a natural (Neumann) boundary condition:
If instead the intrinsic (physical) heat flux \(\varvec{\hat{q}}\) is prescribed, a Robin-type boundary condition is obtained:
where the boundary \(\hat{\varGamma }_{\mathrm{N}_\theta }\) was renamed \(\hat{\varGamma }_{\mathrm{R}_\theta }\).
In order to state the final version of the weak form, trial and test spaces are introduced for the respective solution fields \(\varvec{\hat{u}}(\varvec{\hat{X}},t)\) and \(\bar{\theta }(\varvec{\hat{X}},t)\):
The exact meaning of sufficiently regular is not elaborated here (see eg. Brenner and Scott [16]). The weak form of the ALE boundary value problem derived in the previous section can now be stated as: Find \(\varvec{\hat{u}}\in \varvec{\mathcal {V}}_u\) and \(\bar{\theta }\in \mathcal {V}_\theta \) such that
where the residuals are obtained by inserting the aforementioned Robin-type boundary conditions into the integral expressions in Eqs. (26), (27):
3.3 Finite element formulation
A finite element formulation of the problem based on plane strain and linear elasticity is now presented. Voigt matrix notation is employed. Displacement and temperature fields are approximated by piecewise linear or piecewise quadratic functions: Shape function matrices for displacement and temperature are denoted by \(\underline{\varvec{N}}_u\) and \(\underline{\varvec{N}}_{\theta }\), respectively. Furthermore, \(\underline{\varvec{B}}_{u}:=\underline{\varvec{\hat{\nabla }}}_u\underline{\varvec{N}}_u\) and \(\underline{\varvec{B}}_{\theta }:=\underline{\varvec{\hat{\nabla }}}_\theta \underline{\varvec{N}}_{\theta }\), where
Inserting solution field approximations and employing Galerkin test functions yields the FE formulation
where
Here, \(({\mathsf {{\mathbf {E}}}}^{\mathrm{TOT}})_{ijkl} = E_{ijkl}-\hat{\rho }\delta _{ik}\bar{v}_j\bar{v}_l\) (\(\underline{\varvec{E}}^{\mathrm{TOT}}\) is the Voigt matrix representation of \({\mathsf {{\mathbf {E}}}}^{\mathrm{TOT}}\)), \(\underline{\varvec{1}}=[1\,\,1\,\,0\,\,0]^{\mathrm {T}}\), and \(\underline{\varvec{\bar{v}}}_{\mathrm{l}}\) and \(\underline{{\varvec{\bar{v}}}}_r\) are the Voigt matrix representations of the tensors \(\delta _{ij}\bar{v}_k\) and \(\delta _{ij}(D_t\bar{v}_k-(\bar{v}_k\bar{v}_l)_{,l})\), respectively.
In the above FE formulation, the “\(u\theta \)”- and “\(\theta u\)”-terms represent the thermomechanical coupling effects previously described under Eq. (24).
Recall from Sect. 3.1 that the time dependence of the problem is confined to the solution fields and the loads when the translational and rotational motion of the system is constant in time. It is clear from the above that this property is manifested as time-independent matrices in the FE formulation.
In the stationary case, the FE equations reduce to the time-independent system
4 Element choice and numerical stabilization
Previous studies [12] indicated that, at least for rolling speeds up to the order of a few hundred km/h, no stability problems arise related to the discretized momentum balance equation for the present implementation. By contrast, various numerical problems have been found to have a prominent influence for the discretized energy balance equation, even for very modest rolling speeds. The numerical problems are manifested as node-to-node oscillations in the plate domain and oscillations together with a damped temperature profile in the cylinder domain. The former case, involving a uniform convective velocity field that intersects the boundaries of the domain, is well understood and amenable to a standard application of the SUPG method. The implementation and performance of this method will not be elaborated further in this paper, see instead the references below. The latter case—involving circular, closed convective streamlines—has been found to pose more of a challenge to these techniques, however.
The numerical stabilization methods employed in this paper is the SUPG method (see Donéa and Huerta [17] and Codina et al. [18] (for quadratic elements) ) and an approach employing a variant of residual-free bubbles [19, 20].
The employed bubble function approach bears similarities to that of Brezzi et al. [21], and is implemented as follows: In each triangular element, an additional node is inserted, resulting in a subdivision into three triangles (see Fig. 2). The extra node is positioned along the directed line segment represented in the figure by a dashed arrow. This line segment passes through the element centroid (the black dot) and is parallel with the direction of the convective velocity evaluated at the centroid. The position of the node along this line segment is chosen to correspond to the stationary point of the analytical solution along the line segment, of the pertinent 1D convection-diffusion problem. The shape functions related to this node (the bubble functions) thus serve as a rough approximation of the shape of the solution in the element. Further, their support coincides with the given element, so static condensation can be used to keep the global degree of freedom set unchanged. The bubbles will be chosen as piecewise polynomials of the same order as that of the global approximation (even though it is possible to choose these functions independently).
Illustration of local element subgrid used in the bubble function scheme
The local subgrid is treated as a standard FE mesh—no two shape functions are nonzero at any node (not even the added node). This means that the stated subgrid enrichment scheme is equivalent to a standard Galerkin formulation featuring an enriched discrete function space (i.e. on a refined mesh) [22]. The choice of the positions of the extra nodes in this refined mesh have been informed by appropriate observations of the convective velocity field, as discussed above.
To illustrate the aforementioned numerical difficulties arising for sufficiently high convective velocities in the cylinder domain, a simple Eulerian formulation of stationary, pure heat transfer is considered (cf. Eq. (23)):
where \(\theta \) is the temperature, \(\varvec{q}\) is the heat flux and \(s\) is the external heat source. Further,
where \(\rho \) is the density, \(c\) is the mass-specific heat capacity and \(\varvec{\bar{v}}\) is the convective velocity. A two-dimensional annular domain is considered, in which the convective velocity field is
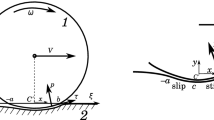
where \(\omega \) is the angular velocity, \(r\) is the distance from the center and \(\varvec{e}_{\varphi }\) is the circumferential unit vector. The temperature is fixed to zero at both the inner and the outer boundary and the external heat source \(s\) is uniform. Figure 3 shows a schematic illustration of the considered problem.
Illustration of the problem used to study the influence of numerical instability
It is noted that the geometry, boundary conditions and loads result in a problem that is one-dimensional (radially symmetric) and has an analytical solution independent of \(\omega \) [23].
Results presented below correspond to a finite element solution of Eq. (35). The mesh used (deliberately unstructured) is shown in Fig. 4. Gaussian quadrature of order 5 (7 integration points) is employed. Unless otherwise stated, the parameters used are as follows: Outer and inner radii of the cylinder \(r_{\mathrm{o}} = 50\) cm and \(r_{\mathrm{i}} = 5\) cm and external heat source \(s = 1000\) Wm\(^{-3}\). Material parameters are chosen to represent a standard steel material.
Mesh used for the annular domain
Figure 5a, b show the temperature distribution along the radial line segment \(x = 0\), \(y < 0\) for varying \(\omega \) and for linear and quadratic shape functions, respectively. Figures 6, 7 show the same thing, but implementing a SUPG stabilization method and the stated bubble function method, respectively.
Temperature distribution along radial line segment for the studied test problem. No numerical stabilization. a Linear elements, b Quadratic elements
Temperature distribution along radial line segment for the studied test problem. SUPG stabilization. a Linear elements. b Quadratic elements
Temperature distribution along radial line segment for the studied test problem. Bubble function stabilization. a Linear elements. b Quadratic elements
The decay (due to spurious numerical dissipation) of the solution for an increasing rotation speed \(\omega \) is clear from Fig. 5, as is the presence of numerical oscillations. As seen in Fig. 6, the SUPG method is able to smooth out the response, but unable to deal with the numerical damping effect: instead seemingly exacerbating it. The same can in general be said for the bubble function approach using linear elements (Fig. 7a), while the use of quadratic elements seems to work much better (see Fig. 7b). It should be noted that an integration order of at least four was found to be necessary in the latter case: below that, the solution started to decay.
In summary, the following choice of element and stabilization scheme has been found to be the most effective in reducing the influence of the aforementioned numerical issues: linear elements and a SUPG method in the plate domain (details not shown here), quadratic elements and a bubble function scheme such as described above in the cylinder domain (see Figs. 5, 6, 7). An integration order of four for the Gauss quadrature is used. Due to the similarity between the problem studied here and the rolling contact problem studied in Sect. 6, it is likely that the scheme described above will be suitable also for the latter, although a mesh convergence study is necessary to ascertain numerically robust results for the specific cases studied.
Remark 3
A comparison between Figs. 5b and 7b shows that the implemented bubble function scheme serves to reduce both the spurious numerical oscillations and the amount of spurious numerical dissipation. It is plausible that an unbiased mesh refinement scheme—where the extra node is instead placed in the centroid of each element—would provide a stronger reduction of the numerical dissipation, but at the cost of a poorer ability of diminishing the numerical oscillations. The test problem studied here exhibits a high degree of symmetry, which means that the influence of numerical instability (oscillatory behaviour) is especially weak. A problem that is more true to life is likely to be less symmetrical and thus more sensitive to numerical instability. The need for the stabilizing effect of the bubble function scheme would be clearer in such a case.
5 Contact formulation
The employed contact formulation is presented below in the context of the ALE description. As the focus of this paper lies elsewhere than in realistic contact interface modelling, the simplest possible laws are chosen for this purpose. However, it is emphasized that the computational framework has been constructed with modularity and extensibility in mind. The implementation of more complex contact laws should therefore be straightforward. Examples of more advanced mechanical/thermal contact interface laws (for frictionless contact), based on microgeometrical and statistical considerations, can be found in [24–28]. Furthermore, [29] is noted, in which homogenization of thermal contact resistances is suggested.
The presentation given below of the mechanical and thermal components of the implemented contact formulation relies heavily on concepts described in Wriggers [8].
5.1 Mechanical contact formulation
A standard penalty method is employed for the formulation of normal mechanical contact. This involves applying a penalty traction at each point \(\varvec{\hat{X}}\in \hat{\varOmega }\) on the cylinder surface (here denoted the “slave” surface) that, in the deformed configuration \(\hat{\omega }\), penetrates the plate surface (here denoted the “master” surface). This traction is proportional to the gap function \(g\) (the negative of the penetration distance) and is directed normal to the master surface. An opposing traction is applied at the point \(\varvec{\hat{X}}^{\mathrm{m}}(\varvec{\hat{X}}) = \varvec{\hat{\varphi }}^{-1}(\varvec{\hat{x}}^{\mathrm{m}}(\varvec{\hat{x}}))\) on the master surface, i.e. the point in \(\hat{\varOmega }\) corresponding to \(\varvec{\hat{x}}^{\mathrm{m}}(\varvec{\hat{x}})\): the normal projection of \(\varvec{\hat{x}}= \varvec{\hat{\varphi }}(\varvec{\hat{X}})\) on the deformed master surface. Assigning superscripts “s” and “m” to terms related to the slave and master surfaces, respectively, enables formulation of the normal contact tractions as
where \(\varvec{\hat{n}}\) is the normal of the deformed master surface at \(\varvec{\hat{X}}^{\mathrm{m}}(\varvec{\hat{X}})\), \(\hat{\varGamma }_\mathrm{cand}^\mathrm{s}\) is the candidate contact surface subset of the slave surface \(\partial \hat{\varOmega }^{\mathrm{s}}\) and
is the scalar \(\varvec{\hat{n}}\)-component of the normal contact force acting on the slave surface. Here, \(\epsilon \) is the penalty stiffness,
is the gap function corresponding to the pair of points \(\varvec{\hat{X}}\) and \(\varvec{\hat{X}}^{\mathrm{m}}(\varvec{\hat{X}})\) and \(\langle \cdot \rangle \) are Macaulay brackets. Note that in theory, \(\lim _{\epsilon \rightarrow \infty }g=0\). In a practical numerical implementation, an increased penalty stiffness \(\epsilon \) leads to a decreased absolute value of the gap function, but an excessive increase leads to ill-conditioning of the discretized equation system. \(\epsilon \) is typically taken as mesh-dependent, scaling inversely with some measure of the mesh size (thus having a higher value in more refined regions) [8]. For the purposes of the current implementation, the simple choice \(\epsilon = \epsilon _n/h\) is deemed adequate, where \(\epsilon _n\) is a constant and \(h\) is a local measure of mesh size. Note that this choice results in the desired property \(\lim _{h\rightarrow 0}\epsilon =\infty \Rightarrow \lim _{h\rightarrow 0}g=0\).
If \(\hat{\varGamma }_\mathrm{c}^\mathrm{s}\subset \hat{\varGamma }_\mathrm{cand}^\mathrm{s}\) is the contact surface—the subset of the slave surface corresponding to negative gap functions—the contribution to the weak form residual (30) due to the contact tractions is
Introducing Galerkin test functions (\(\delta \varvec{\hat{u}}\rightarrow \underline{\varvec{N}}_u\underline{\varvec{c}}_u\)) results in the following contribution to the left-hand side of the finite element formulation (33a):
At this point, the discretization of the master and slave surfaces is introduced. Linear contact elements are used regardless of the order of the elements used for the discretization of the contacting bodies. This is for compability reasons in case the latter discretizations are of different orders. The above expression is in this context evaluated via a one-point quadrature scheme with the integration points coinciding with the nodes of the discretized slave surface (see Wriggers [8]). The result is the finite element load vector pertaining to the normal mechanical contact interaction, to be added to the right-hand side of Eq. (33)a:
Here, \(g_i = g(\varvec{\hat{X}}_{a_i})\), \(\underline{\varvec{n}}_i = \underline{\varvec{n}}(\varvec{\hat{X}}_{a_i})\), \(W_i\) are integration weights (related to edge element lengths) and \(\{a_i\}_{i=1}^{n_c}\) is the active set: the set of nodes in contact. \(\varvec{\hat{X}}_{a_i}^{\mathrm{m}}\) and \(\varvec{\hat{X}}_{a_i}\) are the undeformed positions of the respective points \(\varvec{\hat{x}}_{a_i}^\mathrm{m}\) and \(\varvec{\hat{x}}_{a_i}\) in the deformed configuration, where \(\varvec{\hat{x}}_{a_i}^\mathrm{m}\) is the point on the master surface closest to the point \(\varvec{\hat{x}}_{a_i}\). Figure 8 illustrates a contact element in the deformed discretized domain. Here, \(W_i = \frac{1}{2}(W_i^\mathrm{l} + W_i^\mathrm{r})\).
The \(i\):th contact element. The length of the master element is \(L_i\)
5.2 Thermal contact formulation
The formulation of thermal conduction in the contact region is derived in a manner analogous to the case of normal mechanical contact. A “penalty” heat flux proportional to the temperature difference is imposed on surfaces in contact:
where \(k_c\) is the (velocity-independent) contact conductivity and
is the temperature difference. Note that perfect thermal contact is represented by \(\lim _{k_c\rightarrow \infty }\varDelta \theta =0\). That is, the contact conductivity \(k_c\) would play a role similar to that of the penalty stiffness \(\epsilon \) in the mechanical normal contact formulation. However, \(k_c\) should here in general be interpreted as a physical conductivity pertaining to the surface properties at the contact. In reality, this parameter exhibits a complex dependence on e.g. microgeometry, third body characteristics and contact pressure. However, following the stated ambition to keep the contact interface model as simple as possible, \(k_c\) is taken as constant. This choice is adequate for the purposes of the present paper, but would obviously be an oversimplification in implementations striving for more realistic modelling of the contact interface.
The contribution from the contact fluxes to the weak form residual (31) is
Introducing Galerkin test functions (\(\delta \bar{\theta }\rightarrow \underline{\varvec{N}}_{\theta }\underline{\varvec{c}}_\theta \)) and employing one-point quadrature as above yields the finite element load vector pertaining to the interfacial thermal conduction, to be added to the right-hand side of Eq. (33)b:
where, \(\varDelta \bar{\theta }_i = \varDelta \bar{\theta }(\varvec{\hat{X}}_{a_i})\).
5.3 Solution method
The addition of the (generally nonlinear) contact contributions (40) and (44) to the (otherwise linear) FE formulation of the thermomechanical boundary value problem (Eq. (33)) leads to a nonlinear equation system. This system is solved monolithically by the Newton method (which requires linearization of the contact contributions, although these expressions are not shown in this paper).
The employed contact iteration scheme is identical to the one described in Wriggers [8]: In each iteration of the Newton solver, the residual vector and the tangent stiffness matrix are constructed, followed by an update of the solution guess. The construction of the residual and the tangent involves a contact search procedure, a central step of which being the identification of the set of active nodes (using the contact condition \(g_i < 0\)).
6 Numerical investigations
6.1 Numerical model
The following numerical examples are based on a 2D (plane strain) model of an annular cylinder rolling on a plate. Owing to the convective ALE description, the latter can be kept fairly short, regardless of the actual distance traversed by the cylinder during a simulation. As mentioned in Sect. 3, the model features an isotropic, homogeneous, linear elastic material. Pure rolling and constant rolling velocity (velocity of the cylinder centre relative to a fixed coordinate system) are assumed. A vertical distributed load is applied along the inner boundary of the cylinder. In addition, a constant normal heat flux is applied to given sections of the cylinder perimeter (each having an angular extension of \(45^{\circ }\)). Gravitational loads on the bodies are not included. The base of the plate is fixed in all degrees of freedom and the cylinder inner boundary is fixed in the horizontal direction. All other boundaries are free. The temperature at the plate ends is fixed (to the reference temperature) while all other boundaries (not in contact) are thermally insulated. Figure 9 shows a schematic illustration of the geometry, boundary conditions and loads in the employed model. It is noted that these exhibit vertical symmetry.
Schematic illustration of the thermomechanical model. A applied mechanical load, B cylinder inner boundary (fixed in horizontal direction), C artificial plate domain ends (fixed temperature), D plate base (fixed in all degrees of freedom), E interfaces with prescribed heat flux
A standard parameter setup (used in the following simulations unless otherwise indicated) is now defined. Material parameters for cylinder and plate are: Young’s modulus \(E = 200\) GPa, Poisson’s ratio \(\nu = 0.3\), specific heat capacity \(c = 460\,\hbox {Jkg}^{-1}\,\hbox {K}^{-1}\), thermal conductivity \(k = 45\, \mathrm{W}\hbox {m}^{-1}\hbox {K}^{-1}\), thermal expansion coefficient \(\alpha = 4.8\,{\cdot }\, 10^{-6}\,\hbox {K}^{-1}\), density \(\rho = 8\cdot 10^{3} \hbox {kgm}^{-3}\). Outer and inner radii of the cylinder are \(r_{\mathrm{o}} = 50\) cm and \(r_{\mathrm{i}} = 5\hbox { cm}\), respectively. The height of the plate is \(h = 0.1\) m and the width of the plate domain is chosen as \(b = 1\) m. The contact conductivity is \(k_c = 10^{7}\) \(\hbox {Wm}^{-2}\,\hbox {K}^{-1}\) and the penalty stiffness is \(\epsilon _N = 5\) TN/m. The reference (environmental) temperature is \(\theta ^{\mathrm{ref}}= 293 \text { K}\). The mechanical load is \(P = 10\) kN/m and the heat flux into the cylinder at each interface E is \(W_\mathrm{in} = 30\) W/m.
The rolling velocity is chosen as constant with magnitude \(\bar{v}\) = 50 km/h. The rotational velocity of the cylinder is then \(\bar{v}/r_{\mathrm{o}}\), due to the assumption of pure rolling.
As mentioned in the discussion following Eq. (24), the Gough–Joule effect is negligible for thermoelastic materials. It will therefore not be modeled in the following numerical examples.
Much of the following presentation will study the weighted mean temperature \(\bar{\theta }_\mathrm{m}\), which for an arbitrary domain \(V_0\) can be defined as
where \(|V_0|\) is the volume of \(V_0\). In the following, \(V_0\) will be chosen to represent the cylinder domain and the plate domain, alternatively. It should here be emphasized that in the latter case, the magnitude of the resulting mean temperature is rather arbitrary, since it depends strongly on the volume of the arbitrary domain over which the mean is taken.
6.2 Discretization
The finite element formulation of the problem is implemented in MATLAB. The element type used is a triangular element with two or one degrees of freedom per node in the mechanical and thermal problems, respectively. The approximation for both displacements and temperatures is piecewise linear in the plate and piecewise quadratic in the cylinder. Note that the discrepancy in element order between cylinder and plate has implications for the contact formulation. The approach taken here is to regard both domains as linear as far as the contact formulation is concerned (as was discussed in Sect. 5.1).
The employed mesh is shown in Fig. 10. The mesh of the cylinder is constructed from a coarse basic mesh which is refined according to the following scheme: successive refinement in a series of gradually smaller domains centered at the point of initial contact \(\rightarrow \) global refinements (2 are here used) \(\rightarrow \) refinement of the largest elements along the periphery. After that, all nodes are remapped radially so that the outer nodes describe a circle. At this point, even though measures have been taken to ensure that the outer boundary is as round as possible despite local refinement near the contact region (via peripheral refinement), the centroid is inevitably slightly displaced compared to that of the enclosing circle. This has the effect of making the resultant of the centrifugal force vector (the second component of the vector \(\underline{\varvec{f}}_{uv}\), see Eqs. (33), (26)) nonzero, which is unphysical for a circular domain. Further, this causes considerable errors in the contact computation. For this reason, the inner boundary is rigidly moved so that the position of the centroid of the discretized domain is corrected (thus slightly modifying the geometry). The positions of the inner nodes of the mesh are then determined by linear elastic equilibrium.
The employed finite element mesh, with a zoomed-in view of the refined contact region
The plate domain mesh is constructed by starting from a structured mesh and refining it locally in a rectangular area centered at the point of initial contact. This area extends a distance \(2d_{\mathrm{c}}\) horizontally and \(d_{\mathrm{c}}\) vertically, where \(d_{\mathrm{c}}\) is an analytical prediction (using Hertz theory) of the contact patch size. The minimum allowed size for an element in the final mesh of the plate is 1.5 times the size of the largest element in the cylinder mesh in the most refined region.
All mesh refinements are performed according to Rivara’s longest-edge refinement technique [30], and the final mesh contains 8017 elements and 12608 nodes.
6.3 Numerical stabilization
SUPG stabilization is employed in the plate (linear elements) and a bubble function scheme (according to the description in Sect. 4) is used in the cylinder (quadratic elements). An integration order of four is employed for the Gauss quadrature.
6.4 Convergence study
A mesh convergence study is performed in which the number of global refinements of the cylinder mesh, \(n_{\mathrm{r}}\), is varied. Figure 11 shows a plot of the temperature along the radial line segment \(x = 0\), \(y < 0\) (see Fig. 3) for varying values of \(n_{\mathrm{r}}\). Note that the horizontal axis represents the distance \(r\) from the cylinder center. The range is here limited to \(r_{\mathrm{o}} - d_{\mathrm{c}}/5 < r < r_{\mathrm{o}}\). These results indicate that the employed choice \(n_{\mathrm{r}} = 2\) results in a mesh that is sufficiently fine for the purposes of the subsequent numerical investigations.
Mesh convergence study
6.5 Stationary analysis
Figure 12 shows the stationary temperature distribution in two small regions close to the contact patch (each having the dimensions 2 mm \(\times \) 1 mm). The regions are displaced to the left: the middle of the contact patch is highlighted by a vertical gray mark. The combined influence of heat flux across the contact interface and convective effects is here evident. In particular, the skewing influence of the latter, despite the symmetrical boundary conditions and loads, is noted.
Zoomed in plot of temperature distribution in cylinder and plate [K]. The center of the contact patch (to the right in the figure) is highlighted by a vertical gray mark
Figure 13 shows a comparison between the computed normal contact stress distribution and the analytical Hertzian solution [6, 31]. It is clear from the close correspondence between the two curves that the influence of thermomechanical effects on the mechanical solution is not enough to visibly affect the contact stress distribution.
Normal contact stress distribution
6.5.1 Influence of rolling speed
Figure 14 shows weighted mean temperatures of cylinder and plate (calculated using Eq. (45) for each subdomain) versus the rolling speed. The figure shows that the model is successful in capturing the effect of an increased cooling rate of the cylinder with increasing rolling speed (even with a velocity-independent contact conductivity \(k_c\)). Note that the free boundary of the cylinder is insulated, implying that the cause of the cylinder mean temperature decrease can only be a higher heat flux through the contact interface, in turn caused by a decreased local temperature in the plate at the contact due to an increased convection in the plate. Furthermore, the latter phenomenon leads to a higher rate of heat extraction out of the modeled plate domain (which is bounded by the artificial edges denoted by C in Fig. 9). This explains the significant decrease in mean temperature in the plate with increasing rolling speed, seen in the figure.
Weighted mean temperatures of cylinder and plate versus rolling speed
6.5.2 Influence of thermal contact conductivity
Figures 15 (top) and (middle) show weighted mean temperatures in cylinder and plate, respectively, versus the contact conductivity \(k_c\). Figure 15 (bottom) shows the temperature difference between the cylinder and plate nodes of initial contact. The temperatures in cylinder and plate are seen to approach each other (although the increase in temperature in the plate is very slight), and a saturation effect can be observed from the graphs. It can be concluded that the interval \(k_c>10^7\) Wm\(^{-2}\) K\(^{-1}\) may be considered as resulting in a state of perfect thermal contact. A similar behaviour was observed in Vernersson [3], where a numerical model of wheel–rail heat transfer was used to model the rail chill effect on tread braked railway wheels.
Weighted mean temperatures of cylinder (top) and plate (middle) versus contact conductivity. Bottom temperature difference between the cylinder and plate nodes of initial contact versus contact conductivity
6.5.3 Influence of mechanical load
Figures 16 (top) and (middle) show weighted mean temperatures in cylinder and plate, respectively, for varying applied mechanical load. Figure 16 (bottom) shows the contact patch width. The redistribution of temperature between cylinder and plate as the applied load increases is clear from the two upper graphs (although, also in this case, the change in mean temperature in the plate is very small), and is due to the increased contact patch width (as seen in the lower graph). Note that this effect would have been even stronger had the contact conductivity been modeled as pressure-dependent.
Weighted mean temperatures of cylinder (top) and plate (middle) versus applied mechanical load. Bottom size of contact patch versus applied load
6.6 Transient analysis
For the transient simulations, a backward Euler time integration scheme is used. Three different scenarios involving transient processes are simulated: (i) the external heat flux \(W_\mathrm{in}\) is applied at time \(t\) = 0, (ii) the external heat flux is retracted at \(t\) = 0, (iii) a sharp hole of width 0.2 mm in the plate is traversed. In all cases, the appropriate stationary solution (i.e. featuring i: \(W_\mathrm{in} = 0\), ii/iii: \(W_\mathrm{in} = 30\) W/m) is employed as the initial configuration.
The plate profile used in case iii is implemented in the manner described in Draganis et al. [12], which in turn is based a methodology described in Thompson [32]. In this approach, a given offset function is imposed on the gap functions (38), effectively resulting in a modified plate profile. As time progresses, this profile will be advected through the computational domain. This approach is limited in that there is no actual modification of the plate domain—only of the gap functions. However, where applicable (e.g. when the analysis is focused on contact pressures and/or resultant contact forces), it is highly preferable to actual modifications of the computational domain in the context of an ALE description, due to the intrinsic difficulty of tracking material boundaries in this case.
In cases i and ii, the time evolution of the weighted mean temperatures in both bodies is studied, while in case iii, the analysis is focused on the evolution of contact stresses and -forces as the hole in the plate is traversed. The former phenomenon occurs on a vastly larger time scale than the latter. The time steps used in the respective cases are i/ii: \(\varDelta t = 500\) s and iii: \(\varDelta t = 10^{-6}\) s. These time step sizes have been verified (details not given here) to give a numerically convergent response with respect to phenomena of interest in the present analysis. It is noted that the former time step size implies that the cylinder undergoes many revolutions per time step. In particular, this means that the simulation is unable to resolve mechanical phenomena in this case, which occur on vastly smaller time scales. However, their influence on the studied quantity in cases i and ii: the comparatively very slow evolution of the temperature distribution, is negligible. Taking into account also that the constitutive model does not include inelastic material parameters, it is concluded that the given choice of time step is admissible in this case.
Figure 17 shows the time evolution of the weighted mean temperatures in cylinder and plate for the respective cases i, ii. Figure 17a also shows the stationary solution for reference. Due to the large difference in magnitude of the cylinder and plate temperatures (discussed in previous sections), a logarithmic axis is used for the vertical axis in these figures. The exponential decay of the temperature in 17b is noted. Figure 18 shows the contact stress distribution at four distinct points in time as the hole is traversed. Figure 19 shows the time evolution of the resultant contact force. Note that in order to resolve higher frequencies of the oscillations resulting from the contact interaction at the discontinuity, a smaller time step would be required.
Time evolution of weighted mean temperatures in cylinder and plate. a External heat flux applied at \(t = 0\). b External heat flux retracted at \(t = 0\)
Normal contact stress distribution at four distinct points in time as the hole is traversed
Time evolution of contact force resultant as the hole is traversed
7 Concluding remarks
A theoretical and computational framework governing thermomechanically coupled transient rolling contact based on an ALE kinematical description has been developed. The ALE formulation allows for linearization of the mechanical response, localized mesh refinement and a compact computational domain. Further, it was shown to simplify the time-description of the transient rolling contact problem and enable the formulation of the stationary rolling problem as time-independent.
Numerical simulations featuring both mechanical and thermal loads were performed. The results showed the thermomechanical contact model (featuring a velocity-independent contact conductivity) to be able to capture the effect of convective chilling of the cylinder due to the contact with the plate. A study of the influence of the contact conductivity was performed, and results were found to correspond qualitatively to results in the literature. Further, the relation between the magnitude of the heat flux through the contact interface and the applied mechanical load (owing to the influence of the latter on the contact patch width) was emphasized. Transient simulations showed the model to be able to capture phenomena occurring on disparate time scales, as well as simulations featuring very rough contact geometries.
The convective ALE formulation of the energy balance equation was found to be sensitive to stability problems and other numerical issues in its discretized form. Numerical stabilization techniques were implemented, satisfyingly addressing these problems. Since the numerical issues manifest themselves in essentially different ways in the two domains (due to the differences in the convective velocity fields), the numerical stabilization techniques implemented in these domains had to be designed thereafter.
Upcoming work will be focused on modelling frictional contact. Particular applications of interest include modelling of stick/slip phenomena and frictional heat generation.
Notes
\(\varvec{X}\) held fixed.
\(\otimes \) denotes the dyadic product.
References
Vernersson T et al (2010) Wheel tread damage: a numerical study of railway wheel tread plasticity under thermomechanical loading. Proc IME Part F J Rail Rapid Transit 224(5):435–443. doi:10.1243/09544097JRRT358
Johnson KL (1989) The strength of surfaces in rolling contact. Proc IME Part C J Mech Eng Sci 203(3):151–163. doi:10.1243/PIME_PROC_1989_203_100_02
Vernersson T (2006). Tread braking of railway wheels-noise-related tread roughness and dimensioning wheel temperatures. Field tests, rig measurements and numerical simulations. PhD thesis, Chalmers University of Technology
Teimourimanesh S, Lundén R, Vernersson T (2010). Tread braking of railway wheels-state-of-the-art survey. In: Proceedings 6th European conference on braking JEF2010, pp 293–302
Hertz H (1882) Über die Berührung fester elastischer Körper (On the contact of elastic solids). J Reine Angew Math 92: 156–171
Johnson KL (1987) Contact mechanics. Cambridge University Press, Cambridge. ISBN: 9780521347969
Kalker JJ (1990) Three-dimensional elastic bodies in rolling contact. In: Gladwell GML (ed) Solid mechanics and its applications. Kluwer Academic Publishers, Dordrecht. ISBN: 9780792307129
Wriggers P (2006) Computational contact mechanics. Springer, Berlin. ISBN: 9783540326083
Nackenhorst U (2004) The ALE-formulation of bodies in rolling contact theoretical foundations and finite element approach. Comput Methods Appl Mech Eng 193:299–4322. doi:10.1016/j.cma.2004.01.033
Ziefle M, Nackenhorst U (2008) Numerical techniques for rolling rubber wheels: treatment of inelastic material properties and frictional contact. Comput Mech 42(3):337–356. doi:10.1007/s00466-008-0243-9, ISSN 0178-7675
Suwannachit A, Nackenhorst U (2013) A novel approach for thermomechanical analysis of stationary rolling tires within an ALE-kinematic framework. Tire Sci Technol 41(3):174–195
Draganis A, Larsson F, Ekberg A (2012) Numerical evaluation of the transient response due to non-smooth rolling contact using an arbitrary Lagrangian-Eulerian formulation. Proc IME Part J J Eng Tribol 226(1):36–45. doi:10.1177/1350650111422015
Ottosen NS, Ristinmaa M (2005) The mechanics of constitutive modeling. Elsevier, Amsterdam. ISBN: 9780080446066
Holzapfel GA (2000) Nonlinear solid mechanics: a continuum approach for engineering. Wiley, Chichester. ISBN: 9780471823193
Schweizer B, Wauer J (2001) Atomistic explanation of the Gough–Joule-effect. Eur Phys J B 23(3):383–390. doi:10.1007/s100510170058, ISSN: 1434-6028
Brenner SC, Scott LR (2008) The mathematical theory of finite element methods. In: Marsden JE, Sirovich L, Antman SS (eds) Texts in applied mathematics, vol 15, 3rd edn. Springer, New York. doi:10.1007/978-0-387-75934-0, ISBN: 978-0-387-75933-3
Donéa J, Huerta A (2003) Finite element methods for flow problems. Wiley, Chichester. ISBN: 9780471496663
Codina R, Onate E, Cervera M (1992) The intrinsic time for the streamline upwind/Petrov–Galerkin formulation using quadratic elements. Comput Methods Appl Mech Eng 94(2):239–262. doi:10.1016/0045-7825(92)90149-E, ISSN: 0045-7825
Brezzi F et al (1992) A relationship between stabilized finite element methods and the Galerkin method with bubble functions. Comput Methods Appl Mech Eng 96(1):117–129. doi:10.1016/0045-7825(92)90102-P, ISSN: 0045-7825
Baiocchi C, Brezzi F, Franca LP (1993) Virtual bubbles and Galerkin-least-squares type methods (Ga.L.S.). Comput Methods Appl Mech Eng 105(1):125–141. doi:10.1016/0045-7825(93)90119-I, ISSN: 0045-7825
Brezzi F, Marini D, Russo A (1998) Applications of the pseudo residual-free bubbles to the stabilization of convection-diffusion problems. Comput Methods Appl Mech Eng 166(1–2):51–63. Advances in Stabilized Methods in Computational Mechanics. doi:10.1016/S0045-7825(98)00082-6, ISSN: 0045-7825
Brezzi F et al (2003) Link-cutting bubbles for the stabilization of convection-diffusion-reaction problems. Math Models Methods Appl Sci 13(3):445–461. doi:10.1142/S0218202503002581 [cited By (since 1996)25]
Hetnarski RB, Eslami R (2008) Thermal stresses-advanced theory and applications. In: Gladwell GML (ed) Solid mechanics and its applications. Springer, New York. ISBN: 9781402092466
Schrefler BA, Zavarise G (1993) Constitutive laws for normal stiffness and thermal resistance of a contact element. Comput-Aided Civ Infrastruct Eng 8(4):299–308. doi:10.1111/j.1467-8667.tb00215.x, ISSN: 1467-8667
Wriggers P, Zavarise G (1993) Application of augmented Lagrangian techniques for non-linear constitutive laws in contact interfaces. Commun Numer Methods Eng 9(10): 815–824. doi:10.1002/cnm.1640091005, ISSN: 1099-0887
Wriggers P, Zavarise G (1993) Thermomechanical contact—a rigorous but simple numerical approach. Comput Struct 46(1):47–53. doi:10.1016/0045-7949(93)90166-B, ISSN: 0045-7949
Zavarise G et al (1992) A numerical model for thermomechanical contact based on microscopic interface laws. Mech Res Commun 19(3):173–182. doi:10.1016/0093-6413(92)90062-F, ISSN: 0093-6413
Zavarise G et al (1992) Real contact mechanisms and finite element formulation—a coupled thermomechanical approach. Int J Numer Methods Eng 35(4):767–785. doi:10.1002/nme.1620350409, ISSN: 1097-0207
Temizer I, Wriggers P (2010) Thermal contact conductance characterization via computational contact homogenization: a finite deformation theory framework. Int J Numer Methods Eng 83(1):27–58. doi:10.1002/nme.2822, ISSN: 1097-0207
Rivara MC (1984) Algorithms for refining triangular grids suitable for adaptive and multigrid techniques. Int J Numer Methods Eng 20(4):745–756. doi:10.1002/nme.1620200412, ISSN: 1097-0207
Timoshenko SP, Goodier JN (1951) Theory of elasticity. Engineering societies monographs. McGraw-Hill, New York
Thompson DJ (1991) Theoretical modelling of wheel-rail noise generation. Proc IME Part F J Rail Rapid Transit 205(2):137–149. doi:10.1243/PIME_PROC_1991_205_227_02
Acknowledgments
The project is financed by the Swedish Research Council (www.vr.se) under contract 2008-3860 and is a part of the ongoing activities in the National Centre of Excellence CHARMEC (www.chalmers.se/charmec).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Draganis, A., Larsson, F. & Ekberg, A. Finite element analysis of transient thermomechanical rolling contact using an efficient arbitrary Lagrangian–Eulerian description. Comput Mech 54, 389–405 (2014). https://doi.org/10.1007/s00466-014-0992-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-014-0992-6