Fatigue crack growth simulations of interfacial cracks in bi-layered FGMs using XFEM

Abstract

An investigation of fatigue crack growth of interfacial cracks in bi-layered materials using the extended finite element method is presented. The bi-material consists of two layers of dissimilar materials. The bottom layer is made of aluminium alloy while the upper one is made of functionally graded material (FGM). The FGM layer consists of 100 % aluminium alloy on the left side and 100 % ceramic (alumina) on the right side. The gradation in material property of the FGM layer is assumed to be exponential from the alloy side to the ceramic side. The domain based interaction integral approach is extended to obtain the stress intensity factors for an interfacial crack under thermo-mechanical load. The edge and centre cracks are taken at the interface of bi-layered material. The fatigue life of the interface crack plate is obtained using the Paris law of fatigue crack growth under cyclic mode-I, mixed-mode and thermal loads. This study reveals that the crack propagates into the FGM layer under all types of loads.

Appendices

Appendix A: XFEM formulation

1.1 Governing equations

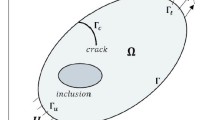
A planar domain $(\Omega )$ bounded by contour $\Gamma$ divided into three parts i.e., $\Gamma _u,\,\Gamma _t$ and $\Gamma _c$ with internal flaws is shown in Fig. 5. The displacement boundary conditions are imposed on $\Gamma _u$, while tractions are applied on $\Gamma _t$ and traction free condition are imposed on crack surfaces $\Gamma _c$. The equilibrium and boundary conditions for this problem may be described as

$$\begin{aligned}&\nabla .{\varvec{\sigma }} +\mathbf{b}=\mathbf{0}\;\text{ in}\;\Omega \end{aligned}$$

(19a)

$$\begin{aligned}&{\varvec{\sigma }}. {\hat{\mathbf{n}}} = {\bar{\mathbf{t}}}\;\text{ on}\;\Gamma _{t}\end{aligned}$$

(19b)

$$\begin{aligned}&{\varvec{\sigma }} .{\hat{\mathbf{n}}}=\mathbf{0}\;\text{ on}\;\Gamma _{c} \end{aligned}$$

(19c)

$$\begin{aligned}&\mathbf{u}={\hat{\mathbf{u}}}\;\text{ on}\;\Gamma _{u} \end{aligned}$$

(19d)

where ${\varvec{\sigma }}$ is the Cauchy stress tensor, $\mathbf{u}$ is the displacement field vector, $\mathbf{b}$ is the body force vector per unit volume, ${\bar{\mathbf{t}}}$ is the external traction vector and ${\hat{\mathbf{n}}}$ is the unit outward normal vector. For small displacements, strain-displacement relation can be described as

$$\begin{aligned} {\varvec{\upvarepsilon }} = {\varvec{\upvarepsilon }} (\mathbf{u}) = \nabla _\mathbf{s} \mathbf{u} \end{aligned}$$

(20)

where $\nabla _s$ is the symmetric part of the gradient operator.

Fig. 5

Domain with discontinuities

The constitutive relations for the linear elastic FGM under consideration is given by Hook’s law

$$\begin{aligned} {\varvec{\sigma }} (\mathbf{u}) =D(\mathbf{x}):{\varvec{\upvarepsilon }(u)} \end{aligned}$$

(21a)

where $\mathbf{x}$ is the vector of $x$ and $y$-coordinates, $D(\mathbf{x})$ is the constitutive matrix, which can be written for plane strain condition as

$$\begin{aligned} D(\mathbf{x})&= \frac{E(\mathbf{x})}{\left\{ {1-2\nu (\mathbf{x})} \right\} \left\{ {1+\nu (\mathbf{x})} \right\} }\nonumber \\&\times \left[ {{ \begin{array}{lll} {1-\nu (\mathbf{x})}&{} {\nu (\mathbf{x})}&{} 0 \\ {\nu (\mathbf{x})}&{} {1-\nu (\mathbf{x})}&{} 0 \\ 0&{} 0&{} {\frac{1-2\nu (\mathbf{x})}{2}} \\ \end{array}}} \right] \end{aligned}$$

(21b)

1.2 Variational formulation

Let the space for admissible displacement fields $\lambda$ be defined by Moes et al. [11]

$$\begin{aligned} \lambda =(\mathbf{v}\in \delta |\mathbf{v}={\bar{\mathbf{u}}}\;\text{ on}\;\Gamma _u )\;\text{ and}\;\mathbf{v}\;\text{ discontinuous} \text{ on}\;\Gamma _{c} \end{aligned}$$

(22a)

where the space $\delta$ is related to the regularity of the solution. In the same way, the test function space $\lambda _0$ may be defined as

$$\begin{aligned} \lambda _0 =(\mathbf{v} \in \delta |\mathbf{v} = 0\;\text{ on}\;\Gamma _u)\; \text{ and}\;\mathbf{v}\;\text{ discontinuous} \text{ on}\;\Gamma _{c} \nonumber \\ \end{aligned}$$

(22b)

A weak form of the equilibrium equation can be written as

$$\begin{aligned} \int \limits _\Omega {{\varvec{\sigma }}\,(\mathbf{u}) : {\varvec{\upvarepsilon }}\,(\mathbf{v})d\varOmega =\int \limits _{\Omega } {\mathbf{b} \cdot \mathbf{v}d\varOmega +\int \limits _{\varGamma _{t}} {{\bar{\mathbf{t}}} \cdot \mathbf{v} d\varGamma }}} \end{aligned}$$

(23)

Substituting the constitutive relation ${\varvec{\sigma }} (\mathbf{u}) =D(\mathbf{x}):{\varvec{\upvarepsilon }} (\mathbf{u})$ in the above equation, we obtain

$$\begin{aligned} \int \limits _{\Omega } {{\varvec{\upvarepsilon }} (\mathbf{u}): D(\mathbf{x}) :{\varvec{\upvarepsilon }} (\mathbf{v})d\varOmega =\int \limits _{\Omega } {\mathbf{b} \cdot \mathbf{v} d\Omega +\int \limits _{\varGamma _{t}} {{\bar{\mathbf{t}}}\cdot \mathbf{v} d\varGamma }}} \end{aligned}$$

(24)

The linear form, $\stackrel{\frown }{T}$ and the bilinear form, $\stackrel{\frown }{S}$ of the above equation are obtained as

$$\begin{aligned}&\stackrel{\frown }{T} (\mathbf{v}) = \int \limits _{\varGamma } {\mathbf{b} \cdot \mathbf{v}d\varOmega +\int \limits _{\varGamma _{t}} {{\bar{\mathbf{t}}} \cdot \mathbf{v}d\Omega }} \end{aligned}$$

(25)

$$\begin{aligned}&\stackrel{\frown }{S} (\mathbf{u,v}) = \int \limits _{\varOmega } {{\varvec{\upvarepsilon }}(\mathbf{u}) :D(\mathbf{x}): {\varvec{\upvarepsilon }}(\mathbf{v})d \Omega } \end{aligned}$$

(26)

The quadratic energy functional can be written as

$$\begin{aligned} \Pi (\mathbf{u})=\frac{1}{2}\stackrel{\frown }{S} (\mathbf{u,u})-\stackrel{\frown }{T} (\mathbf{u}) \end{aligned}$$

(27)

On substitution of the relevant quantities, the expression for the same is obtained as

$$\begin{aligned} \Pi (\mathbf{u})\!=\!\frac{1}{2}\int \limits _\Omega {{\varvec{\upvarepsilon }}(\mathbf{u}): D(\mathbf{x}) :{\varvec{\upvarepsilon }}(\mathbf{u})d\Omega \!-\!\int \limits _{\varGamma } {\mathbf{b}\cdot \mathbf{u} d\lambda \!-\!\int \limits _{\varGamma _{t}} {{\bar{\mathbf{t}}}\cdot \mathbf{u} d\lambda }}} \nonumber \\ \end{aligned}$$

(28)

By substituting the trial and test functions and taking variation of the above equation, the following set of discrete equations is obtained using the arbitrariness of nodal variations

$$\begin{aligned} \left[ \mathbf{K} \right] \left\{ \mathbf{d} \right\} =\left\{ \mathbf{f} \right\} \end{aligned}$$

(29)

where d is the vector of nodal unknowns, K and f are the global stiffness matrix and the external force vector respectively. The stiffness matrix and force vector are computed on element level, and are assembled into their global counterparts through usual finite element assembly procedure.

1.3 Displacement approximation

For modeling cracks in XFEM [4, 11], the approximation function takes the following form

$$\begin{aligned} \mathbf{u}^{h}(\mathbf{x})=\sum _{i=1}^{n} {N_i (\mathbf{x})\left[ {{\bar{\mathbf{u}}}_i +\underbrace{H(\mathbf{x})\mathbf{a}_i}_{i\in n_r }+\underbrace{\sum _{j=1}^4 {\beta _j (\mathbf{x})\mathbf{b}_i^j}}_{i\in n_A}} \right] } \end{aligned}$$

(30a)

where $i$ is the set of all nodes in the domain, $N_i$ (x) is the element shape function associated with node $i$ satisfying the partition of unity criterion, ${\bar{\mathbf{u}}}_i$ is the nodal displacement vector associated with the continuous part of the finite element solution, $\mathbf{a}_i$ denotes the additional unknown degrees of freedom associated with the discontinuous Heaviside function $H(\mathbf{x})$, and is defined for those elements, which are completely cut by the crack to account for the jump in the displacement field, $\mathbf{b}_{i}^{j}$ is the additional degrees of freedom associated with those elements, which are partially cut by the crack, and accounts for stress singularity at the crack tip, $n$ is the set of all nodes in the mesh, $n_{r}$ is the set of nodes belonging to those elements which are completely cut by the crack, and $n_{A}$ is the set of nodes belonging to those elements which are partially cut by the crack. In Eq. (30a), the first term represents the standard finite element approximation, the second term represents the enrichment for those elements which are completely cut by the crack, and the third term represents the enrichment for those elements which contain the crack tip. For any node $n_{r}$, Heaviside jump function, $H(\mathbf{x})$ takes a constant value, and is equal to +1 on one side and -1 on other side of the crack. Also, the standard displacements do not correspond to the displacements computed by XFEM. Thus, a shifted enrichment is used. If $\mathbf{x}_{i}$ is the node of interest then Eq. (30a) can be written as

$$\begin{aligned} \mathbf{u}^{h}(\mathbf{x})&= \sum _{i=1}^{n} N_{i} (\mathbf{x})\left[ {\bar{\mathbf{u}}}_i +\underbrace{[\mathrm{H}(\mathbf{x})-H(\mathbf{x}_i )]\mathbf{a}_i }_{i\in n_r} \right. \nonumber \\&\left. +\underbrace{\sum _{j=1}^4 {[\beta _j (\mathbf{x})-\beta _j (\mathbf{x}_i )]\mathbf{b}_i^j}}_{i\in n_A} \right] \end{aligned}$$

(30b)

In Eq. (30b), the difference between the values of the Heaviside function at the evaluation (Gauss) point and nodal point is taken to maintain the partition of unity. The tip enrichment is performed for those elements which contain the crack tip, and is achieved by adding additional function derived from the theory of linear elastic fracture mechanics available in the literature [2].

For isotropic and bi-layered FGM, the crack tip enrichment functions are same as that of the homogenous materials [14], and are obtained from the displacement solution of a linear elastic crack in the infinite plate [2].

$$\begin{aligned}&\beta _{j} (\mathbf{x})\nonumber \\&\quad =\left[ {\sqrt{r}\sin \frac{\theta }{2},\sqrt{r}\cos \frac{\theta }{2},\sqrt{r}\cos \frac{\theta }{2}\sin \theta ,\sqrt{r}\sin \frac{\theta }{2}\sin \theta } \right] \nonumber \\ \end{aligned}$$

(30c)

1.4 XFEM formulation for cracks in FGM

Using the approximation function defined in Eq. (30b) for a crack, the elemental matrices, $\mathbf{K}^{e}$ and $\mathbf{f}^{e}$ are obtained as

$$\begin{aligned} \mathbf{f}^{e}&= \left\{ \mathbf{f}_\mathbf{i}^\mathbf{u} \quad \mathbf{f}_\mathbf{i}^\mathbf{a} \quad \mathbf{f}_\mathbf{i}^{\mathbf{b1}} \quad \mathbf{f}_\mathbf{i}^{\mathbf{b2}} \quad \mathbf{f}_\mathbf{i}^{\mathbf{b3}} \quad \mathbf{f}_\mathbf{i}^{\mathbf{b4}} \right\} ^{T}\;\text{ and} \nonumber \\ \mathbf{K}_{ij}^e&= \left[ {{\begin{array}{lll} {K_{ij}^{uu}}&{} {K_{ij}^{ua}}&{} {K_{ij}^{ub}} \\ {K_{ij}^{au}}&{} {K_{ij}^{aa}}&{} {K_{ij}^{ab}} \\ {K_{ij}^{bu}}&{} {K_{ij}^{ba}}&{} {K_{ij}^{bb}} \\ \end{array}}} \right] \end{aligned}$$

(31a)

The sub-matrices and vectors that appear in the foregoing equations are given by

$$\begin{aligned} \mathbf{K}_{ij}^{rs}&= \int \limits _{\Omega ^{e}} {(\mathrm{B}_{i}^{r})} ^{T}\mathbf{D}\,\mathrm{B}_j^s d\Omega \quad \text{ where},\;r,s=u,a,b \end{aligned}$$

(31b)

$$\begin{aligned} \mathbf{f}_i^u&= \int \limits _{\Omega ^{e}} {\mathrm{N}_i \mathbf{b}\,d\Omega } +\int \limits _{\Gamma _t} {\mathrm{N}_i {\bar{\mathbf{t}}}\,d\Gamma } \end{aligned}$$

(31c)

$$\begin{aligned} \mathbf{f}_i^a&= \int \limits _{\Omega ^{e}} {\mathrm{N}_i (H(\mathbf{x})-H(\mathbf{x}_i )) \mathbf{b}\,d\Omega } \nonumber \\&\quad +\int \limits _{\Gamma _t} {\mathrm{N}_i (H(\mathbf{x})-H(\mathbf{x}_i )) {\bar{\mathbf{t}}}d\Gamma } \end{aligned}$$

(31d)

$$\begin{aligned} \mathbf{f}_i^{b\stackrel{\frown }{\alpha }}&= \int \limits _{\Omega ^{e}} {\mathrm{N}_i \beta _{\stackrel{\frown }{\alpha }} ((\mathbf{x})-(\mathbf{x}_i )) \mathbf{b}\,d\Omega } \nonumber \\&\quad +\int \limits _{\Gamma _t} {\mathrm{N}_i (\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x})-(\mathbf{x}_{i})) {\bar{\mathbf{t}}}\, d\Gamma }\quad \text{ where},\;\stackrel{\frown }{\alpha } =1, 2, 3, 4 \nonumber \\ \end{aligned}$$

(31e)

where $N_i$ are finite element shape function, $\text{ B}_{i}^{u},\,\text{ B}_{i}^{a},\,\text{ B}_{i}^{b}$ and $\text{ B}_i^{b\stackrel{\frown }{\alpha }}$ are the matrices of shape function derivatives given by

$$\begin{aligned} \text{ B}_{i}^{u}&= \left[ {{\begin{array}{l} {N_{i,x}} \\ 0 \\ {N_{i,y}} \\ \end{array}}} \right. \left. {{\begin{array}{l} 0 \\ {N_{i,y}} \\ {N_{i,x}} \\ \end{array}}} \right] \end{aligned}$$

(31f)

$$\begin{aligned} \text{ B}_{i}^{a}&= \left[ {{\begin{array}{l} {\left( {N_{i} (H(\mathbf{x})-H(\mathbf{x}_i ))} \right) _{,x}} \\ 0 \\ {\left( {N_{i} (H(\mathbf{x})-H(\mathbf{x}_i ))} \right) _{,y}} \\ \end{array}}} \right. \left. {{\begin{array}{l} 0 \\ {\left( {N_{i} (H(\mathbf{x})-H(\mathbf{x}_i ))} \right) _{,y}} \\ {\left( {N_{i} (H(\mathbf{x})-H(\mathbf{x}_i ))} \right) _{,x}} \\ \end{array}}} \right] \nonumber \\ \end{aligned}$$

(31g)

$$\begin{aligned} \text{ B}_{i}^{b \stackrel{\frown }{\alpha }}&= \left[ {{\begin{array}{l} {\left( {N_{i} (\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x})-\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x}_i ))} \right) _{,x}} \\ 0 \\ {\left( {N_{i} (\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x})-\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x}_i ))} \right) _{,y}} \\ \end{array}}} \right. \left. {{\begin{array}{l} 0 \\ {\left( {N_{i} (\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x})-\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x}_i ))} \right) _{,y}} \\ {\left( {N_{i} (\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x})-\beta _{\stackrel{\frown }{\alpha }} (\mathbf{x}_i ))} \right) _{,x}} \\ \end{array}}} \right] , \nonumber \\&\stackrel{\frown }{\alpha } =1,2,3,4 \end{aligned}$$

(31h)

After obtaining the numerical formulations, Eq. (29) is solved to obtain the nodal displacements, and then strains and stresses are evaluated through post-processing. The difference between the solution for a homogenous material and FGM lies in the fact that the material properties are a function of the space variable. After obtaining the values of stress and strain components, the values of stress intensity factor are evaluated using domain based interaction integral approach.

Appendix B: Computation of stress intensity factors for FGMS

For an elastic body subjected to thermo-mechanical load (Fig. 6), a quantity ${J}^{\prime }$ (equivalent to $J$-integral) is given by

$$\begin{aligned} {J}^{\prime } = \oint \limits _{\Gamma _{o}} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_{i}}{\partial x_{1}}} \right) n_{j} d\Gamma } \end{aligned}$$

(32)

where $\mathbf{x}=[x_{1}\quad x_{2}]^{T}\equiv [x\quad y]^{T},\,\tilde{W}$ is the strain energy density function and $n_{j}$ is the $j$th component of the outward unit vector normal to an arbitrary closed contour $\Gamma _o$ enclosing the area $A_o$. The ${J}^{\prime }$ in Eq. (32) can be converted into domain form using divergence theorem,

$$\begin{aligned} {J}^{\prime } = \int \limits _{A_o} {\left( {\frac{\partial \tilde{W}}{\partial x_1 } - \frac{\partial \sigma _{ij}}{\partial x_j} \frac{\partial u_i }{\partial x_1}- \sigma _{ij} \frac{\partial ^{2}u_i}{\partial x_1 \partial x_j}} \right) dA} \end{aligned}$$

(33)

Fig. 6

Path $\Gamma _{o}$ surrounding an enclosed area $A_{o}$

In Eq. (33), $\frac{\partial \sigma _{ij}}{\partial x_{j}} \frac{\partial u_{i}}{\partial x_1} =0$ from equilibrium equations. For a linear elastic material subjected to thermo-mechanical load, $\tilde{W}$ can be written as

$$\begin{aligned} \tilde{W} = \frac{1}{2}\sigma _{ij}\;\varepsilon _{ij}^{m} = \frac{1}{2} C_{ijkl}\;\varepsilon _{kl}^{m}\;\varepsilon _{ij}^{m} \end{aligned}$$

(34a)

$$\begin{aligned} \text{ where},\;\varepsilon _{ij}^{m} =\varepsilon _{ij} -\gamma \Delta T\delta _{ij} \end{aligned}$$

(34b)

$\gamma$ is the coefficient of thermal expansion and $\Delta T$ is the temperature difference. Now from Eq. (34a), we get

$$\begin{aligned} \frac{\partial \tilde{W}}{\partial x_1}=\frac{1}{2}\frac{\partial C_{ijkl}}{\partial x_1}\,\varepsilon _{kl}^{m}\,\varepsilon _{ij}^{m} +\sigma _{ij} \frac{\partial \varepsilon _{ij}^{m}}{\partial x_1} \end{aligned}$$

(34c)

From Eq. (34b), we get $\frac{\partial \varepsilon _{ij}^{m}}{\partial x_{1}}=\frac{\partial \varepsilon _{ij}}{\partial x_{1}}-\frac{\partial \gamma }{\partial x_{1}}\Delta T\delta _{ij} -\gamma \frac{\partial \Delta T}{\partial x_{1}}\delta _{ij}$

Now, Eq. (34c) becomes

$$\begin{aligned} \frac{\partial \tilde{W}}{\partial x_1}&= \frac{1}{2}\frac{\partial C_{ijkl}}{\partial x_1}\varepsilon _{kl}^{m}\,\varepsilon _{ij}^{m} +\sigma _{ij} \frac{\partial \varepsilon _{ij}}{\partial x_1 }\nonumber \\&-\,\sigma _{ij} \left( {\gamma \frac{\partial \Delta T}{\partial x_1 }+\frac{\partial \gamma }{\partial x_1}\Delta T} \right) \delta _{ij} \end{aligned}$$

(34d)

Substituting $\frac{\partial \tilde{W}}{\partial x_1}$ from Eq. (34d) into Eq. (33), we arrive at,

$$\begin{aligned} {J}^{\prime } = \int \limits _{A_o} {\left( {\frac{1}{2}\frac{\partial C_{ijkl} }{\partial x_1}\varepsilon _{ij}^{m} \varepsilon _{kl}^{m} -\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}} \right) dA} \end{aligned}$$

(34e)

Hence,

$$\begin{aligned} {J}^{\prime }&= \oint \limits _{\Gamma _o} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&= \int \limits _{A_o} {\left( {\frac{1}{2}\frac{\partial C_{ijkl}}{\partial x_1}\varepsilon _{ij}^{m} \varepsilon _{kl}^{m} -\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}} \right) dA} \end{aligned}$$

(35)

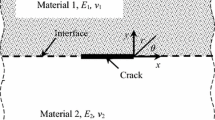
Now consider bi-material cracked body consisting of two functionally graded materials as shown in Fig. 7. The crack is lying at the interface of two materials along $x$-axis. For an enclosed area $A_o^{m1}$ surrounded by a closed path ($a\rightarrow b\rightarrow \Gamma _2^{m1} \rightarrow c\rightarrow d\rightarrow \Gamma _{1}^{m1})$ as shown in Fig. 7, Eq. (35) can be rewritten as

$$\begin{aligned} {J}^{\prime }_1&= \int \limits _{ab} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma }\nonumber \\&\quad +\int \limits _{\Gamma _2^{m1}} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&\quad +\int \limits _{cd} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma }\nonumber \\&\quad +\int \limits _{\Gamma _1^{m1}} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&= \int \limits _{A_o^{m1}} {\left( {\frac{1}{2}\frac{\partial C_{ijkl} }{\partial x_1}\varepsilon _{ij}^{m} \varepsilon _{kl}^{m} -\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}} \right) dA} \end{aligned}$$

(36)

Fig. 7

Path independent closed contour around the crack tip

Similarly, for an enclosed area $A_{o}^{m2}$ as shown in Fig. 7 surrounded by a closed path2 $(d\rightarrow c\rightarrow \Gamma _{2}^{m2} \rightarrow e\rightarrow f\rightarrow \Gamma _{1}^{m2})$, Eq. (36) can be written as

$$\begin{aligned} {J}^{\prime }_2&= \int \limits _{dc} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma }\nonumber \\&+\int \limits _{\Gamma _2^{m2}} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&\quad + \int \limits _{ef} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&\quad +\int \limits _{\Gamma _1^{m2}} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&= \int \limits _{A_o^{m2}} {\left( {\frac{1}{2}\frac{\partial C_{ijkl} }{\partial x_1}\varepsilon _{ij}^{m}\,\varepsilon _{kl}^{m} -\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}} \right) dA} \end{aligned}$$

(37)

Let $\stackrel{\frown }{F} =\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right)$ and $\stackrel{\frown }{G} =\left( {\frac{1}{2}\frac{\partial C_{ijkl} }{\partial x_1} \upvarepsilon _{ij}^{m}\,\varepsilon _{kl}^{m} -\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}} \right)$. Now combining Eqs. (36) and (37), we get

$$\begin{aligned} {J}^{\prime }&= \int \limits _{ab} {\stackrel{\frown }{F} n_{j} d \Gamma } +\int \limits _{\Gamma _2^{m1}} {\stackrel{\frown }{F} n_{j} d \Gamma } +\int \limits _{cd} {\stackrel{\frown }{F} n_{j} d \Gamma } \nonumber \\&\quad +\int \limits _{\Gamma _1^{m1}} {\stackrel{\frown }{F} n_{j} d \Gamma } + \int \limits _{dc} {\stackrel{\frown }{F} n_{j} d \Gamma } \nonumber \\&\quad +\int \limits _{\Gamma _2^{m2}} {\stackrel{\frown }{F} n_{j} d \Gamma } +\int \limits _{ef} {\stackrel{\frown }{F} n_{j} d \Gamma } \nonumber \\&\quad +\int \limits _{\Gamma _1^{m2}} {\stackrel{\frown }{F} n_{j} d \Gamma } =\int \limits _{A_o^{m1}} {\stackrel{\frown }{G} dA} +\int \limits _{A_o^{m2}} {\stackrel{\frown }{G} dA} \end{aligned}$$

(38)

where ${J}^{\prime } = {J}^{\prime }_1 +{J}^{\prime }_2$. If $\Gamma _{1} =\Gamma _{1}^{m1} +\Gamma _{1}^{m2},\,\Gamma _{2} =\Gamma _{2}^{m1} +\Gamma _{2}^{m2},\,A_{1} =A_{1}^{m1} +A_{1}^{m2},\,A_{2} = A_{2}^{m1} + A_{2}^{m2},\,A_{o}^{m1} =A_{2}^{m1} -A_{1}^{m1},\,A_{o}^{m2} =A_{2}^{m2} -A_{1}^{m2},\,A_{o} = A_{2} -A_{1} =A_{o}^{m1} +A_{o}^{m2}$, then Eq. (38) reduces to

$$\begin{aligned} {J}^{\prime }&= \int \limits _{ab} {\stackrel{\frown }{F} n_{j} d \Gamma } +\int \limits _{\Gamma _2} {\stackrel{\frown }{F} n_j d \Gamma } +\int \limits _{cd} {\stackrel{\frown }{F} n_{j} d \Gamma } +\int \limits _{\Gamma _1} {\stackrel{\frown }{F} n_{j} d \Gamma } \nonumber \\&\quad +\int \limits _{dc} {\stackrel{\frown }{F} n_{j} d \Gamma } +\int \limits _{ef} {\stackrel{\frown }{F} n_{j} d \Gamma } =\int \limits _{A_o} {\stackrel{\frown }{G} dA} \end{aligned}$$

(39)

In Eq. (39), $\int _{ab} {\stackrel{\frown }{F} n_{j} d \Gamma } =0$ and $\int _{ef} {\stackrel{\frown }{F} n_{j} d \Gamma } =0$ as $\sigma _{ij} n_j =0$, and $\tilde{W} \delta _{1j} n_j d\Gamma =\tilde{W}dx_2 =0$.

Moreover, $\int _{cd} {\stackrel{\frown }{F} n_{j} d \Gamma } \!+\!\int _{dc} {\stackrel{\frown }{F} n_{j} d \Gamma } \!=\!0$ as $\tilde{W} \delta _{1j} n_j d \Gamma \!=\!0$ and $\sigma _{ij} n_j \frac{\partial u_i}{\partial x_1}$ is continuous across the perfect interface between two functionally graded materials. Finally Eq. (39) reduces to

$$\begin{aligned} {J}^{\prime }&= \int \limits _{\Gamma _2} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_{j} d \Gamma } \nonumber \\&\quad +\int \limits _{\Gamma _1} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&= \int \limits _{A_o} {\left( {\frac{1}{2}\frac{\partial C_{ijkl} }{\partial x_1}\varepsilon _{ij}^{m}\,\varepsilon _{kl}^{m} -\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}} \right) dA} \end{aligned}$$

(40)

Since, $A_o =A_2 -A_1$ and changing the direction of arrow on $\Gamma _1$, above equation reduces to

$$\begin{aligned}&\int \limits _{\Gamma _2} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&\quad -\int \limits _{\Gamma _1} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma }\nonumber \\&\quad +\int \limits _{A_2 -A_1} {\left( {\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}-\frac{1}{2}\frac{\partial C_{ijkl} }{\partial x_1}\varepsilon _{ij}^m \varepsilon _{kl}^m} \right) dA} =0 \end{aligned}$$

(41)

Equation (41) can be further simplified as

$$\begin{aligned}&\int \limits _{\Gamma _2} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma }\nonumber \\&\quad +\int \limits _{A_2} {\left( {\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}-\frac{1}{2}\frac{\partial C_{ijkl}}{\partial x_1 }\varepsilon _{ij}^{m} \varepsilon _{kl}^m} \right) dA}\nonumber \\&=\int \limits _{\Gamma _1} {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_i}{\partial x_1}} \right) n_j d \Gamma } \nonumber \\&\quad +\int \limits _{A_1} {\left( {\sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_1}-\frac{1}{2}\frac{\partial C_{ijkl}}{\partial x_1 }\varepsilon _{ij}^m \varepsilon _{kl}^m} \right) dA} \end{aligned}$$

(42)

Hence, for a bi-layered material of two FGMs having a crack and an interface both along $x_1$-direction, the integral $J=\int _{\Gamma } {\left( {\tilde{W} \delta _{1j} - \sigma _{ij} \frac{\partial u_{i}}{\partial x_{1}}} \right) n_{j} d \Gamma } -\int _{A} \left( \frac{1}{2}\frac{\partial C_{ijkl}}{\partial x_{1}}\varepsilon _{ij}^{m} \varepsilon _{kl}^{m}\right.$ $\left. - \sigma _{kk} \frac{\partial (\gamma \Delta T)}{\partial x_{1}} \right) dA$ is path independent, where $\Gamma$ is a path starting from the lower crack face and terminating on the upper crack face and $A$ is the enclosed area within $\Gamma$.

Further, let $q$ be a weight function such that its value is one at the inner path $\Gamma _1$, zero at the outer path $\Gamma _2$, and arbitrary elsewhere. Now $J$ can be written as

$$\begin{aligned} J&= \int \limits _{\Gamma _1} {\stackrel{\frown }{F} n_{j} d \Gamma } -\int \limits _{A_1} {\stackrel{\frown }{G} dA} \nonumber \\&= -\int \limits _{\Gamma _{2}} {\stackrel{\frown }{F} n_{j} q d \Gamma } -\int \limits _{ef} {\stackrel{\frown }{F} n_{j} qd \Gamma } +\int \limits _{\Gamma _1} {\stackrel{\frown }{F} n_{j} qd \Gamma } \nonumber \\&\quad -\int \limits _{ab} {\stackrel{\frown }{F} n_{j} qd \Gamma } - \int \limits _{A_{1}} {\stackrel{\frown }{G} dA} \end{aligned}$$

(43)

where first integral is zero because $q=0$ on $\Gamma _2$, and second and fourth integrals are also zero because the integrands are zero on the crack faces. Eq. (43) can be written as

$$\begin{aligned} J=-\oint {\stackrel{\frown }{F} qn_j d \Gamma } - \int \limits _{A_1} {\stackrel{\frown }{G} dA} \end{aligned}$$

(44)

where first term in Eq. (44) represents a closed contour enclosing the area $A_o$, and $A_1$ represents the enclosed area inside the contour $\Gamma _1$. In order to enhance the usefulness of $J$, the form of contour integral is converted to equivalent domain form as

$$\begin{aligned} J=-\int \limits _{A_o} {\frac{\partial }{\partial x_j}\left\{ {\stackrel{\frown }{F} q} \right\} dA} -\int \limits _{A_{1}} {\stackrel{\frown }{G} dA} \end{aligned}$$

(45a)

where $A_o$ is an enclosed area inside the closed contour in Eq. (45a). Let the weight function $q$ takes a value one at the crack tip and zero at the contour $\Gamma _2$. If inner contour $\Gamma _1$ shrink to the crack tip then $A_1= 0,\,A_o =A_2$, and Eq. (45a) may be simplified to

$$\begin{aligned} J=-\int \limits _{A_0} {\frac{\partial }{\partial x_j}\left\{ {\stackrel{\frown }{F} q} \right\} dA} \end{aligned}$$

(45b)

After substituting the value of $\stackrel{\frown }{F}$, Eq. (45b) can be written as

$$\begin{aligned} J=\int \limits _{A_0} {\frac{\partial }{\partial x_j}\left\{ {\left( {\sigma _{ij} \frac{\partial u_i}{\partial x_1}-\tilde{W} \delta _{1j}} \right) q} \right\} dA} \end{aligned}$$

(46)

For calculating the interaction integral for an elastic body, we consider two equilibrium states of the cracked body. State 1 is the actual state with given boundary conditions while state 2 is an auxiliary state. Superscript $a$ represents the parameters for auxiliary state.

• Actual state (State 1):       $\sigma _{ij} \quad \varepsilon _{ij} \quad u_{i} \quad \Delta T \quad \tilde{J}$

• Auxiliary state (State 2):    $\sigma _{ij}^{a} \quad \varepsilon _{ij}^{a} \quad u_{i}^{a} \quad 0 \quad \quad J^{a}$

Defining thermal $J$- integral for both states

$$\begin{aligned}&\tilde{J} = \int \limits _{A_{o}} {\frac{\partial }{\partial x_{j}}\left\{ {\left( {\sigma _{ij} \frac{\partial u_i}{\partial x_1}-\frac{1}{2}\sigma _{ik} \varepsilon _{ik}^{m} \delta _{1j}} \right) q} \right\} dA} \end{aligned}$$

(47a)

$$\begin{aligned}&J^{a} = \int \limits _{A_{o}} {\frac{\partial }{\partial x_{j}}\left\{ {\left( {\sigma _{ij}^{a} \frac{\partial u_{i}^{a}}{\partial x_1 }-\frac{1}{2}\sigma _{ik}^a \varepsilon _{ik}^a \delta _{1j}} \right) q} \right\} dA} \end{aligned}$$

(47b)

The $J$-integral for the two superimposed state will be given as

$$\begin{aligned}&J_T = \int \limits _{A_o} \frac{\partial }{\partial x_j}\left\{ \left( \left( {\sigma _{ij}+\sigma _{ij}^a} \right) \left( {\frac{\partial u_i}{\partial x_1}+\frac{\partial u_i^a}{\partial x_1}} \right) \right. \right. \nonumber \\&\qquad \quad \left. \left. -\frac{1}{2}\left( {\sigma _{ik}+\sigma _{ik}^a} \right) \left( {\varepsilon _{ik}^m +\varepsilon _{ik}^a} \right) \delta _{1j} \right) q \right\} dA \end{aligned}$$

(47c)

$$\begin{aligned} J_T =\tilde{J}+J^{a}+M_{12} \end{aligned}$$

(48)

where

$$\begin{aligned} M_{12}&= \int \limits _{A_o} \frac{\partial }{\partial x_j}\left\{ \left( \sigma _{ij}\frac{\partial u_i^a}{\partial x_1}+\sigma _{ij}^a \frac{\partial u_i}{\partial x_1} \right. \right. \nonumber \\&\quad \left. \left. -\frac{1}{2}\left( {\sigma _{ik}\varepsilon _{ik}^a +\sigma _{ik}^a \varepsilon _{ik}^m} \right) \delta _{1j} \right) q \right\} dA \end{aligned}$$

(49)

where the auxiliary field for the FGM may be taken from Yu et al. [24, 25] as

$$\begin{aligned} \sigma _{ij}^{a}&= C_{ijkl}^{tip} \frac{1}{2}\left( {\frac{\partial u_k^a}{\partial x_l}+\frac{\partial u_l^a}{\partial x_k}} \right) , \varepsilon _{ij}^{a} =S_{ijkl} (\mathbf{x}) \sigma _{kl}^{a}\;\text{ and} \nonumber \\ \varepsilon _{ij}^{a}&\ne \frac{1}{2}\left( {\frac{\partial u_i^a}{\partial x_j}+\frac{\partial u_{j}^{a}}{\partial x_i}} \right) \end{aligned}$$

(50)

Using the following $\sigma _{ik}\varepsilon _{ik}^{a} \!=\!\sigma _{ik} S_{ikpq} (\mathbf{x})\sigma _{pq}^{a} \!=\! \varepsilon _{pq}^{m} \sigma _{pq}^{a} \!=\!\sigma _{ik}^{a} \varepsilon _{ik}^{m}$, Eq. (49) can be written as

$$\begin{aligned} M_{12} =\int \limits _{A_o} {\frac{\partial }{\partial x_j}\left\{ {\left( {\sigma _{ij} \frac{\partial u_i^a}{\partial x_1}+\sigma _{ij}^a \frac{\partial u_i}{\partial x_1} -\sigma _{ik}^a \varepsilon _{ik}^m \delta _{1j}} \right) q} \right\} dA}\nonumber \\ \end{aligned}$$

(51)

Equation (51) can be modified as

$$\begin{aligned} M_{12}&= \int \limits _{A_o} {\left( {\sigma _{ij} \frac{\partial u_i^a }{\partial x_1}+\sigma _{ij}^a \frac{\partial u_i}{\partial x_1} -\sigma _{ik}^a \varepsilon _{ik}^m \delta _{1j}} \right) \frac{\partial q}{\partial x_j} dA} \nonumber \\&\quad + \int \limits _{A_{o}} {\frac{\partial }{\partial x_j}\left( {\sigma _{ij} \frac{\partial u_i^a}{\partial x_1}+\sigma _{ij}^a \frac{\partial u_i}{\partial x_1} -\sigma _{ik}^{a} \varepsilon _{ik}^{m} \delta _{1j}} \right) q\,dA} \nonumber \\ \end{aligned}$$

(52)

Equation (52) can be written as

$$\begin{aligned} M_{12}&= \int \limits _{A_{o}} {\left( {\sigma _{ij} \frac{\partial u_{i}^{a} }{\partial x_1}+\sigma _{ij}^{a} \frac{\partial u_{i}}{\partial x_{1}} -\sigma _{ik}^{a} \varepsilon _{ik}^{m} \delta _{1j}} \right) \frac{\partial q}{\partial x_j} dA} \nonumber \\&\quad + \int \limits _{A_{o}} \left( \frac{\partial \sigma _{ij}}{\partial x_j }\frac{\partial u_i^a}{\partial x_1}+\sigma _{ij}\frac{\partial ^{2}u_i^a}{\partial x_j \partial x_1}+\frac{\partial \sigma _{ij}^a}{\partial x_j}\frac{\partial u_i}{\partial x_1}\right. \nonumber \\&\quad \left. +\sigma _{ij}^{a} \frac{\partial ^{2}u_i}{\partial x_j \partial x_1 }-\frac{\partial \sigma _{ik}^a}{\partial x_1}\varepsilon _{ik}^m -\sigma _{ik}^a \frac{\partial \varepsilon _{ik}^m}{\partial x_1} \right) q\,dA \end{aligned}$$

(53)

Using equilibrium equation, $\frac{\partial \sigma _{ij}}{\partial x_j}\frac{\partial u_{i}^{a}}{\partial x_1}=0$, and $\frac{\partial \sigma _{ij}^{a}}{\partial x_j}\frac{\partial u_i}{\partial x_1}=0$. Due to symmetry of the stress tensor, $\sigma _{ij} \frac{\partial ^{2}u_{i}^{a}}{\partial x_{j} \partial x_{1}}=\sigma _{ij} \frac{1}{2}\frac{\partial }{\partial x_1}\left( {\frac{\partial u_{i}^{a}}{\partial x_j}+\frac{\partial u_{j}^{a}}{\partial x_i}} \right)$ and $\sigma _{ij}^{a} \frac{\partial ^{2} u_{i}}{\partial x_j \partial x_1} = \sigma _{ij}^{a} \frac{\partial \varepsilon _{ij}}{\partial x_1}$. Finally Eq. (52) is simplified as

$$\begin{aligned} M_{12}&= \int \limits _{A_o} {\left( {\sigma _{ij} \frac{\partial u_i^a }{\partial x_1}+\sigma _{ij}^a \frac{\partial u_i}{\partial x_1} -\sigma _{ik}^a \varepsilon _{ik}^m \delta _{1j}} \right) \frac{\partial q}{\partial x_j} dA} \nonumber \\&\quad + \int \limits _{A_o} \left( \sigma _{ij} \frac{1}{2}\frac{\partial }{\partial x_1}\left( {\frac{\partial u_i^a}{\partial x_j }+\frac{\partial u_j^a}{\partial x_i}} \right) \right. \nonumber \\&\quad \left. +\sigma _{ij}^a \frac{\partial }{\partial x_1}\left( {\varepsilon _{ij} -\varepsilon _{ij}^m} \right) -\frac{\partial \sigma _{ik}^a }{\partial x_1}\varepsilon _{ik}^{m} \right) q\,dA \end{aligned}$$

(54)

Using Eq. (50), Eq. (54) can be further simplified as

$$\begin{aligned} M_{12}&= \int \limits _{A_o} {\left( {\sigma _{ij} \frac{\partial u_i^a }{\partial x_1}+\sigma _{ij}^{a} \frac{\partial u_{i}}{\partial x_1} -\sigma _{ik}^{a} \varepsilon _{ik}^{m} \delta _{1j}} \right) \frac{\partial q}{\partial x_j} dA} \nonumber \\&\quad + \int \limits _{A_o} \left( \sigma _{ij} \left( {S_{ijkl}^{tip} -S_{ijkl} (\mathbf{x})} \right) \frac{\partial \sigma _{kl}^a}{\partial x_1} \right. \nonumber \\&\quad \left. +\sigma _{ij}^{a} \left( {\frac{\partial \gamma }{\partial x_1} \Delta T+\gamma \frac{\partial \Delta T}{\partial x_1}} \right) \delta _{ij} \right) q\,dA \end{aligned}$$

(55)