1 Introduction

The stiffness and strength of composites can be increased by using thin fibres as reinforcement. Modelling of such composites can be significantly simplified, assuming that the fibres are perfectly rigid. This assumption can be applied to fibres that are much stiffer than the matrix surrounding them and is now often used to analyse composites reinforced with nanofibres.

Overall effective elastic properties of composites can be obtained using various homogenization methods (see, for example, the handbooks by Nemat-Nasser and Hori [1], Mura [2] and Qu and Cherkaoui [3]). Analytical methods are usually used to analyse single rigid fibres in the infinite domain and computational methods for composites with multiple fibres. Dundurs and Markenscoff [4] applied the method of Green’s function to thin rigid inclusions perfectly attached to the elastic matrix loaded by concentrated forces, dislocations and a concentrated couple to determine stress fields. Li and Ting [5] used the Stroh formalism and Fredholm integral equations to analyse displacement and stress fields for a rigid or an elastic line inclusion in an anisotropic elastic infinite plate uniformly loaded at infinity. Hu et al. [6] analysed the influence of rigid-line fibres and a bi-material interface on stress intensity factors at crack tips using integral equations. Pingle et al. [7] derived the solutions for the rigid-line inclusions using the duality principle. The method was applied to analysis of stresses in the neighbourhood of a fibre and the composite compliance. Gorbatikh et al. [8] studied the influence of stress intensity factors at the tips of rigid fibres on effective compliance of the material. Iorga et al. [9] analysed elastic properties of mostly in-plane random short-length cylindrical fibre composites using the finite element method (FEM). Pike and Oskay [10] presented the application of the extended finite element method (XFEM) for composites with random short and rigid fibres.

The linear-elastic composites with fibres can be simply and accurately modelled by the boundary element method (BEM). The method requires division of composite external surfaces and fibres into boundary elements. Liu et al. [11] used the fast multiple boundary element method (FMBEM) to calculate effective elastic properties of composites reinforced by carbon nanotubes. The composites were treated as three-dimensional structures with a large number of rigid fibres. Dong et al. [12] applied the boundary integral equations to study the effect of positions of cracks and rigid-line inclusions in infinite plates on stress intensity factors. Dong and Lee [13] presented the application of the boundary integral method to analysis of stress intensity factors and effective elastic properties for periodic arrangements of cracks or rigid-line inclusions. Dong [14] used the single-domain and sub-domain BEM to study the influence of positions and material properties of inclusions, cracks and rigid lines on stresses in infinite isotropic plates. Wang and Yao [15] applied the FMBEM to analyse debonding process in carbon nanotube composites. The nanotubes were modelled as rigid fibres. The debonding started when the shear interfacial stress reached a critical value. The effective nonlinear stress–strain relation was obtained. Yao et al. [16] analysed an effect of non-ideal interfacial conditions or additional interfacial layer between deformable fibres and the matrix of carbon nanotube composites on effective Young’s modulus using the FMBEM.

Fedelinski and Gorski [17] applied the coupled finite and boundary element method to maximise stiffness of dynamically loaded plates reinforced by deformable stiffeners. The same approach was used by Fedelinski and Gorski [18] to maximise stiffness of statically loaded nanocomposites. Fedelinski [19] presented plates with rigid straight fibres and cracks modelled by the BEM. The influence of distribution of rigid fibres on effective properties of composites and an influence of positions of a fibre and a crack on stress intensity factors were shown. Fedelinski et al. [20] presented computation of effective elastic properties of composites with planar rigid-surface inclusions using the unit cell method.

The original contribution of this work is an analysis of effective elastic properties of representative volume elements (RVE) of composites with randomly distributed and oriented thin rigid fibres. In this paper, boundary integral equations for composites, equations of rigid body motion of fibres, equilibrium equations of interaction forces between the fibres and the matrix and numerical formulation of the method are shown. The method is used to solve three numerical examples, which demonstrate accuracy and efficiency of the method and their practical significance in numerical homogenization of composites.

2 Boundary integral equations for a composite reinforced by thin rigid fibres

Fedelinski [19] presented the formulation and applications of the BEM for simple analyses of composites with thin rigid fibres. In this work, the formulation is briefly described to make the paper self-contained.

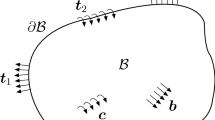
A homogenous, isotropic and linear-elastic plate, shown in Fig. 1, is considered. The plate has the boundary \(\Gamma \) and occupies the domain \(\Omega \). The plate is subjected to static loadings. The boundary tractions \(t_{j}\) are applied along the external boundary \(\Gamma \) and the body forces \(f_{j}\) in the domain \(\Omega \). The boundary tractions \(t_{j}\), the body forces \(f_{j}\) and the displacements \(u_{j}\) fulfil the following boundary integral equation [21]:

$$\begin{aligned}&c_{ij} (\mathbf {x}')u_{j} (\mathbf {x}')+\int \limits _{\Gamma } {T_{ij} (\mathbf {x}',\mathbf {x})u_{j} (\mathbf {x})\text {d}\Gamma (\mathbf {x})}\nonumber \\&\quad =\int \limits _\Gamma {U_{ij} (\mathbf {x}',\mathbf {x})t_{j} (\mathbf {x})\text {d} \Gamma (\mathbf {x})} +\int \limits _\Omega U_{ij} (\mathbf {x}',\mathbf {X})f_{j} (\mathbf {X})\text {d}\Omega (\mathbf {X}), \end{aligned}$$
(1)

where x\('\) is the collocation point, which can be a domain or an internal point, x is the boundary point, X is the domain point, \( c_{ij}\) is a constant, which depends on the position of the point x\('\) (in the case of the boundary point, it depends additionally on the shape and orientation of the boundary), and \(U_{ij}\) and \(T_{ij}\) are the well-known fundamental solutions of elastostatics [21].

Fig. 1
figure 1

Elastic plate

Full size image

Let us now consider the case of a plate reinforced by straight, thin and rigid fibres, as shown in Fig. 2. The fibres are assumed to be perfectly attached to the matrix. The loaded plate deforms and interaction forces occur between the fibres and the matrix. They can be treated as particular body forces \(f_{j}\) distributed only along the fibres. If the interaction forces are the only body forces, then the last integral in Eq. (1) is integrated along the attachment lines. The boundary integral equation for the plate with thin fibres has the following form:

$$\begin{aligned}&c_{ij} (\mathbf {x}')u_{j} (\mathbf {x}')+\int \limits _\Gamma {T_{ij} (\mathbf {x}',\mathbf {x})u_{j} (\mathbf {x})\text {d}\Gamma (\mathbf {x})}\nonumber \\&\quad =\int \limits _\Gamma {U_{ij} (\mathbf {x}',\mathbf {x})t_{j} (\mathbf {x})\text {d} \Gamma (\mathbf {x})} +\sum \limits _{n=1}^N {\int \limits _{\Gamma _{n} } {U_{ij} (\mathbf {x}',\mathbf {X})t_{j}^{n} (\mathbf {X})\text {d}\Gamma _{n} (\mathbf {X})}}, \end{aligned}$$
(2)

where N is the number of fibres, \(\Gamma _{n}\) is the fibre line, and \(t_{j}^{n}\) are the tractions along the fibre.

Fig. 2
figure 2

Composite reinforced by thin rigid fibres

Full size image

3 Displacements and equilibrium equations for thin rigid fibres

The loaded composite deforms and the fibres change their position and orientation (Fig. 3). The displacement components \(u_{i}\)(x) of an arbitrary point x of the straight rigid fibre for a small rotation angle are:

$$\begin{aligned} u_{1} (\mathbf {x})= & {} u_{1} (\mathbf {x}_{o} )-\varphi r(\mathbf {x})\sin \alpha , \end{aligned}$$
(3)
$$\begin{aligned} u_{2} (\mathbf {x})= & {} u_{2} (\mathbf {x}_{o} )+\varphi r(\mathbf {x})\cos \alpha , \end{aligned}$$
(4)

where \(u_{i}(\mathbf{x} _{\mathrm{o}})\) are displacement components of the fibre tip, r is the distance between the point x and the fibre tip \(\mathbf{x} _{o}\), \(\alpha \) is the initial angle between the fibre and the axis \(x_1\) of the global coordinate system, and \(\varphi \) is the rotation angle.

Fig. 3
figure 3

Initial and final position of the rigid fibre

Full size image

The tractions acting on the fibre (Fig. 4) are in equilibrium. They satisfy the following equilibrium equations:

$$\begin{aligned}&\int \limits _{\Gamma _{n}}{t_{1}^{n} (\mathbf {x})\text {d} \Gamma _{n} (\mathbf {x})} =0, \end{aligned}$$
(5)
$$\begin{aligned}&\int \limits _{\Gamma _{n} } {t_{2}^{n} (\mathbf {x})\text {d} \Gamma _{n} (\mathbf {x})}=0, \end{aligned}$$
(6)
$$\begin{aligned}&\int \limits _{\Gamma _{n} } {[-t_{1}^{n} (\mathbf {x})\sin \alpha +t_{2}^{n} (\mathbf {x})\cos \alpha ]r(\mathbf {x})\text {d}\Gamma _{n} (\mathbf {x})} =0. \end{aligned}$$
(7)

The resultant forces acting on the \(x_1\) and \(x_2\) directions [Eqs. (5) and (6)] and the moment of tractions with respect to the fibre tip \(\mathbf{x} _{o}\) [Eq. (7)] are zero.

Fig. 4
figure 4

Tractions acting on the rigid fibre

Full size image

4 Boundary element method for the composite with thin rigid fibres

In order to obtain the numerical solution by the boundary element method, the external boundaries of the plate and the fibres are divided into boundary elements. The displacements, tractions and coordinates of external boundaries and tractions acting on the fibres are interpolated by using nodal values and quadratic shape functions. The displacements and coordinates of fibres are not interpolated because the fibres are rigid and straight. The interpolated displacements, tractions and coordinates are substituted into the boundary integral Eq. (2), and the relations between nodal displacements and tractions are obtained. The collocation points are nodes along the external boundaries of the plate and the fibres.

The displacements of fibre nodes are calculated analytically using Eqs. (3) and (4). The equations for all fibre nodes can be written in the matrix form:

$$\begin{aligned} \mathbf{u}=\mathbf{Iu}_{\mathbf{f}}, \end{aligned}$$
(8)

where the matrix u contains the displacements of fibre nodes, the matrix I depends on the coordinates of nodes, and the matrix \(\mathbf{u} _{\mathbf{f}}\) contains the displacements of fibre tips and the angles of fibre rotations.

The equilibrium equations [Eqs. (5), (6) and (7)] for tractions acting on the fibres can be expressed in the matrix form:

$$\begin{aligned} \mathbf{Et}_{\mathbf{f}} =0, \end{aligned}$$
(9)

where the matrix E depends on the coordinates of fibre nodes and the matrix \(\mathbf{t} _{\mathbf{f}}\) contains nodal values of tractions acting on the fibres. The matrix E is obtained by analytical integration of expressions in Eqs. (5), (6) and (7).

The boundary integrals in Eq. (2) are computed numerically using the Gauss quadrature, and the standard BEM matrix equation is obtained. The displacements of collocation fibre nodes are expressed by Eq. (8). The equilibrium Eq. (9) is added to the system of equations giving the following matrix equation:

$$\begin{aligned} \left[ \begin{array}{cc} \mathbf{H}_{\mathbf{ee}} &{}\quad 0 \\ \mathbf{H}_{\mathbf{fe}} &{}\quad \mathbf{I} \\ 0 &{}\quad 0 \\ \end{array}\right] \left[ \begin{array}{c} \mathbf{u}_{\mathbf{e}} \\ \mathbf{u}_{\mathbf{f}} \\ \end{array}\right] =\left[ \begin{array}{cc} \mathbf{G}_{\mathbf{ee}} &{}\quad \mathbf{G}_{\mathbf{ef}} \\ \mathbf{G}_{\mathbf{fe}} &{}\quad \mathbf{G}_{\mathbf{ff}} \\ 0 &{}\quad \mathbf{E} \\ \end{array}\right] \left[ \begin{array}{c} \mathbf{t}_{\mathbf{e}} \\ \mathbf{t}_{\mathbf{f}} \\ \end{array}\right] , \end{aligned}$$
(10)

where the submatrices with the index e denote the external boundaries and the submatrices with the index f denote the fibres. The submatrices H and G are the standard BEM matrices, which depend on the boundary integrals of fundamental solutions, shape functions and Jacobians [21].

The matrix Eq. (10) is rearranged. The unknown variables should be on the left side and the known boundary conditions on the right side of the equation. The unknown fibre tractions \(\mathbf{t} _{\mathbf{f}}\) and the corresponding column are rearranged as follows:

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbf{H}_{\mathbf{ee}} &{}\quad -\,\mathbf{G}_{\mathbf{ef}} &{}\quad 0 \\ \mathbf{H}_{\mathbf{fe}} &{}\quad -\,\mathbf{G}_{\mathbf{ff}} &{}\quad \mathbf{I} \\ 0 &{}\quad \mathbf{E} &{}\quad 0 \\ \end{array}\right] \left[ \begin{array}{c} \mathbf{u}_{\mathbf{e}} \\ \mathbf{t}_{\mathbf{f}} \\ \mathbf{u}_{\mathbf{f}} \\ \end{array}\right] =\left[ \begin{array}{c} \mathbf{G}_{\mathbf{ee}} \\ \mathbf{G}_{\mathbf{fe}} \\ 0 \\ \end{array}\right] [\mathbf{t}_{\mathbf{e}}]. \end{aligned}$$
(11)

In the case of the mixed boundary conditions on the external boundaries, additionally the matrices \(\mathbf{u} _{\mathbf{e}}\), \(\mathbf{t} _{\mathbf{e}}\) and the corresponding columns of matrices H and G are rearranged, as in the standard BEM [21]. The direct solutions of the matrix equation are the unknown nodal displacements and tractions along the external boundaries and the fibre displacements and tractions. Displacements, strains and stresses at an arbitrary point of the matrix can be computed using the present approach, as shown in [19].

5 Numerical examples

Three numerical examples are considered in this chapter. The first example—a rigid fibre in a circular disc, is used to verify accuracy of the method and study the influence of fibre lengths on disc displacements. In the second example—parallel rigid fibres in a square plate, the influence of fibres direction on elastic effective properties is analysed. The third example shows rigid fibres randomly distributed in a square plate. A large number of representative volume elements of the composite are used to calculate average effective elastic properties. The results for the parallel and randomly distributed fibres are compared.

The material of the matrix is linear-elastic, homogenous and isotropic, its Poisson ratio is \(v=0.3\), and the plates are in plane strain conditions.

5.1 Rigid fibre in a circular disc

Consider a straight rigid fibre with a length of 2a located in the centre of a circular disc with a radius of r, as shown in Fig. 5a. The edge of the disc is loaded by uniformly distributed tractions p in the radial direction and simply supported along the vertical symmetry line.

Fig. 5
figure 5

Rigid fibre in a circular disc—dimensions and boundary conditions: a whole disc, b half of the disc

Full size image

The fibre is inclined with respect to the horizontal axis at the angle \(\alpha = \pi /4\). Six different lengths of the fibre are considered, namely \(a/r=0.3\), 0.4, 0.5, 0.6, 0.7 and 0.8. In order to verify the accuracy, the displacements for the whole disc and the half of the disc are compared. The half of the disc is simply supported along the straight edge and additionally fixed along the fibre, as shown in Fig. 5b. The half of the disc is analysed using the standard BEM code [22]. The whole disc is divided into 58 boundary elements, the half of the disc into 44 boundary elements, including 10 elements for the fibre. The initial and deformed shape of the whole and the half of the plate for the longest considered fibre is shown in Fig. 6. The displacements of points A and B in the local coordinate system \(x_{\mathrm{1}}x_{\mathrm{2}}\) are computed and normalised with respect to the displacement \(u_{o}\) of the disc edge without the fibre and shown in Table 1. The analytical solution for the disc without the fibre is \(u_{o}=(1-2\nu )(1+\nu ) \textit{pr}/E\), where E is the Young’s modulus of the matrix. Very small differences of order 0.1% occur for the displacements \(u_{1}(A)/u_{o}\) and long fibres. The normalised displacements of points A and B versus the relative fibre length are shown in Fig. 7. When the relative length increases from \(a/r=0.3\) to 0.8, the normalised displacement \(u_{1}(A)/u_{o}\) decreases by 50% and \(u_{2}(B)/u_{o}\) increases by 15%. Different orientations of the fibre were analysed by Fedelinski in [23], and the results confirmed high accuracy of the method.

Fig. 6
figure 6

Rigid fibre in a circular disc, \(a/r=0.8\)—initial (dashed line) and deformed shape (continuous line): a whole disc, b half of the disc

Full size image
Fig. 7
figure 7

Normalised relative displacements of points A and B

Full size image
Table 1 Normalised displacements of points A and B for different lengths of the fibre
Full size table

5.2 Parallel rigid fibres in a square plate

Consider a square plate with the dimensions 2w and 2h (\(w=h\)). The plate is reinforced by 25 uniformly distributed parallel straight rigid fibres of length 2a, which are inclined at the angle \(\alpha \), as shown in Fig. 8. The distances between the fibre centres are b and c (\(b=c\)). The following proportions of dimensions are assumed \(b/w=3/8\) and \(a/w=2^{1/2}/8\). The composite with the following orientations of fibres is analysed \(\alpha =0\), \(\pi /12\), \(\pi /6\), \(\pi /4\), \(\pi /3\), \(5\pi /12\), \(\pi /2\) rad. The plate can be treated as the representative volume element (RVE) of the composite. The plate is simply supported. Two types of traction boundary conditions are considered—the plate is subjected to the uniformly distributed horizontal tensile tractions p (Fig. 9a) or shear loading p (Fig. 9c).

Fig. 8
figure 8

Parallel rigid fibres in a square plate

Full size image
Fig. 9
figure 9

Boundary conditions: a horizontal tension, b vertical tension, c shear loading

Full size image

The composite is discretised using 330 boundary elements (80 for the external boundary and 10 for each fibre). The initial and the deformed shape of the composite for the angle of fibres \(\alpha =\pi /4\) subjected to tension or shear loading is shown in Fig. 10.

Fig. 10
figure 10

Parallel rigid fibres in a square plate—initial (dashed line) and deformed shape (continuous line), \(\alpha =\pi /4\): a horizontal tension, b shear loading

Full size image

The boundary displacements of the RVEs are used to compute average strains:

$$\begin{aligned} \bar{{\varepsilon }}_{ij} =\frac{1}{2A}\int \limits _\Gamma {(u_{i} n_{j} +u_{j} n_{i} )\text {d}\Gamma }, \end{aligned}$$
(12)

where A is the area of the RVE, \(\Gamma \) is its boundary, and \(n_{i}\) is the component of the normal outward unit vector to the boundary.

The tractions along the external boundaries of the RVE are used to calculate average stresses:

$$\begin{aligned} \bar{{\sigma }}_{ij} =\frac{1}{A} \int \limits _\Gamma {t_{i} x_{j} \text {d}\Gamma }. \end{aligned}$$
(13)

The relationship between the average strains and average stresses for linear-elastic anisotropic plates can be expressed in the matrix form [24, 25]:

$$\begin{aligned} \left[ \begin{array}{c} \bar{\varepsilon }_{11} \\ \bar{\varepsilon }_{22} \\ 2\bar{\varepsilon }_{12}\\ \end{array}\right] =\left[ \begin{array}{ccc} \frac{1}{E_{1}} &{}\quad -\,\frac{\nu _{21}}{E_{2}} &{}\quad \frac{\eta _{12,1}}{G} \\ -\,\frac{\nu _{12}}{E_{1}} &{}\quad \frac{1}{E_{2}} &{}\quad \frac{\eta _{12,2}}{G} \\ \frac{\eta _{1,12}}{E_{1}} &{}\quad \frac{\eta _{2,12}}{E_{2}} &{}\quad \frac{1}{G_{12}} \\ \end{array}\right] \left[ \begin{array}{c} \bar{\sigma }_{11} \\ \bar{\sigma }_{22} \\ \bar{\sigma }_{12} \\ \end{array}\right] , \end{aligned}$$
(14)

where the square matrix containing elastic properties is the composite effective compliance matrix, \(E_{1}\) and \(E_{2}\) are the Young moduli, \(G_{12}\) is the shear Kirchhoff modulus, \(v_{12}\) and \(v_{21}\) are the Poisson ratios and \(\eta _{1},{12}\), \(\eta _{2},{12}\), \(\eta _{12},{1}\) and \(\eta _{12},{2}\) are the shear-extension coupling coefficients. The first type of boundary conditions (Fig. 9a) is used to compute the effective Young moduli and Poisson ratios, and the second (Fig. 9c) to compute the shear Kirchhoff moduli. Both boundary conditions are used to calculate shear-extension coupling coefficients.

Table 2 Normalised effective elastic properties
Full size table
Fig. 11
figure 11

Normalised effective elastic properties

Full size image
Fig. 12
figure 12

Randomly distributed fibres in a square plate

Full size image
Fig. 13
figure 13

Histogram of the normalised Young modulus \(E_{{1}}/E_{o}\) for parallel fibres

Full size image
Fig. 14
figure 14

Distribution of parallel fibres in the plate subjected to tension—initial (dashed line) and deformed shape (continuous line): a the smallest Young modulus \(E_{{1}}/E_{o}=1.308\), b the largest Young modulus \(E_{{1}}/E_{o}=1.397\)

Full size image
Fig. 15
figure 15

Histogram of the normalised Young modulus \(E_{{1}}/E_{o}\) for randomly oriented fibres

Full size image
Fig. 16
figure 16

Distribution of randomly oriented fibres in the plate subjected to tension—initial (dashed line) and deformed shape (continuous line): a the smallest Young modulus \(E_{{1}}/E_{o}=1.049\), b the largest Young modulus \(E_{{1}}/E_{o}=1.214\)

Full size image
Fig. 17
figure 17

Histogram of the normalised Poisson ratio \(v_{{12}}/v_{o}\) for randomly oriented fibres

Full size image
Fig. 18
figure 18

Distribution of randomly oriented fibres in the plate subjected to tension—initial (dashed line) and deformed shape (continuous line): a the smallest Poisson ratio \(v_{{12}}/v_{o}=0.884\), b the largest Poisson ratio \(v_{{12}}/v_{o}=1.052\)

Full size image
Fig. 19
figure 19

Histogram of the normalised Kirchhoff modulus \(G_{{12}}/G_{o}\) for randomly oriented fibres

Full size image
Fig. 20
figure 20

Distribution of randomly oriented fibres in the plate subjected to shear loading—initial (dashed line) and deformed shape (continuous line): a the smallest Kirchhoff modulus \(G_{{12}}/G_{o}=1.059\), b the largest Kirchhoff modulus \(G_{{12}}/G_{o}=1.177\)

Full size image

Knowing the average strains and stresses for different boundary conditions, the effective elastic properties can be calculated using Eq. 14. The normalised effective properties—the Young modulus \(E_{1}/E_{o}\), the Kirchhoff modulus \(G_{ 12}/G_{o}\), the Poisson ratio \(v_{{12}}/v_{o}\) and the shear-extension coefficients \(\eta _{{1},{12}}\) and \(\eta _{{12},{1}}\), are given in Table 2, where \(E_{o}\), \(v_{o}\) and \(G_{o}\) are properties of the matrix in plane strain conditions. The relationships between normalised effective properties and the angle of the fibres are shown in Fig. 11. The elastic properties \(E_{{2}}\), \(\eta _{{12},{2}}\) and \(\eta _{{2},{12}}\) are not presented. They can be determined by applying vertical tension (Fig. 9b). However, these material constants can be more easily obtained using results presented in Table 2 and the proper orientation of the traction with respect to the fibres. The computed effective elastic properties satisfy the symmetry conditions of the compliance matrix, given by Eq. (14), with high accuracy.

The Young modulus of the composite is 67% higher than the matrix modulus for the fibres parallel to the load direction, equal to the matrix modulus for the angle \(\alpha =\pi /3\) and 8% higher for the perpendicular fibres. The Poisson ratio is equal to the matrix coefficient for the parallel fibres, 10% higher for the angle \(\alpha =\pi /6\) and 36% lower for the perpendicular fibres. The Kirchhoff modulus for the fibres parallel to the plate edges is the same as for the matrix and is 26% larger for the angle \(\alpha =\pi /4\). The shear-extension coupling coefficient \(\eta _{{1},{12}}\) has the largest absolute value for the angle \(\alpha =\pi /12\) and \(\eta _{{1},{12}}\)—for the angle \(\alpha =\pi /6\). Similar variations of off-axis engineering constants with lamina orientation for unidirectional carbon/epoxy, boron/aluminium and glass/epoxy composites are shown in [26].

5.3 Randomly distributed rigid fibres in a square plate

Consider a square plate of dimensions 2w and 2h (\(w=h)\) reinforced by 25 randomly distributed rigid fibres of length 2a, as shown in Fig. 12. The ratio of dimensions is \(a/w=2^{1/2}/8\). The number of fibres, their length and the dimensions of the plate are the same as in the second numerical example; therefore, it is possible to compare the results for randomly and uniformly distributed parallel fibres. The minimal distance between the fibres or the fibres and the external boundary of the plate is b, where \(b/w=1/16\). The plate can be treated as the representative volume element of the composite. The same boundary conditions are applied as in the previous example. The composite is discretised using 330 boundary elements (80 for the external boundary and 10 for each fibre). In order to compute elastic effective properties, 1000 RVEs with randomly distributed fibres are generated. The effective properties are normalised as in the previous example.

In Fig. 13, the histogram of the normalised Young modulus for the parallel fibres to the applied tensile loading in the horizontal direction is shown. The obtained histogram is interpolated by the normal Gaussian distribution. The minimum value of \(E_{{1}}/E_{o}\) is 1.308, the average is 1.353, and the maximum is 1.397. The standard deviation of the results is 0.013. The maximum value is 27% smaller than for the parallel uniformly distributed fibres shown in the second numerical example. The distributions of fibres for the minimum and maximum of \(E_{{1}}/E_{o}\) are shown in Fig. 14. It can be seen that for the plate with the smallest Young modulus, there are large areas of the matrix that is not stiffened by the fibres. In the plate with the largest Young modulus, the fibres are distributed more uniformly. The Poisson ratios \(v_{{12}}/v_{o}\) are 1.000.

The same RVEs are subjected to the vertical tension, as shown in Fig. 9b. The average normalised Young modulus \(E_{{2}}/E_{o}\) in the vertical direction is 1.050, and the average Poisson ratio \(v_{{21}}/v_{o}\) is 0.776. The shear Kirchhoff modulus is the same as the matrix. The shear-extension coupling coefficients are 0. The computed effective elastic properties satisfy the symmetry conditions of the compliance matrix, given by Eq. (14), with high accuracy. As the result of the homogenization of the composite material with thin rigid fibres, the homogenous orthotropic material has been obtained.

In Fig. 15, the histogram of the normalised Young modulus for randomly distributed and oriented fibres is shown. The minimum value of \(E_{{1}}/E_{o}\) is 1.049, the average is 1.118, and the maximum is 1.214. The standard deviation of the results is 0.026. The maximum value is 45% smaller than for the parallel uniformly distributed fibres shown in the second numerical example. The distributions of fibres for the minimum and maximum of \(E_{{1}}/E_{o}\) are shown in Fig. 16. The orientation of fibres in the plate with the largest Young modulus is similar to the direction of the applied tensile load.

In Fig. 17, the histogram of the normalised Poisson ratio for randomly distributed and oriented fibres is shown. The minimum value of \(v_{{12}}/v_{o}\) is 0.884, the average is 0.971, and the maximum is 1.052. The standard deviation of the results is 0.026. The distributions of fibres for the minimum and maximum of \(v_{{12}}/v_{o}\) are shown in Fig. 18. Many of the fibres in the plate with the smallest Poisson ratio are oriented almost perpendicularly to the applied tensile loading.

In Fig. 19, the histogram of the normalised Kirchhoff modulus for randomly distributed and oriented fibres is shown. The minimum value of \(G_{{12}}/G_{o}\) is 1.059, the average is 1.119, and the maximum is 1.177. The standard deviation of the results is 0.019. The maximum value of the Kirchhoff modulus for randomly oriented fibres is 8% lower than for the parallel fibres inclined at the angle \(\alpha =\pi /4\), shown in the second numerical example. The distributions of fibres for the minimum and maximum of \(G_{{12}}/G_{o}\) are shown in Fig. 20.

The same RVEs are subjected to the vertical tension, as shown in Fig. 9b. The average normalised Young modulus \(E_{{2}}/E_{o}\) is 1.118, and the average Poisson ratio \(v_{{21}}/v_{o}\) is 0.971. These material constants are the same as for the loading in the horizontal direction shown earlier. The average shear-extension coupling coefficients are 0. As the result of the homogenization of the composite material with thin rigid fibres, the homogenous isotropic material has been obtained.

6 Conclusions

In the present work, the boundary element method was used to analyse composites with thin rigid fibres. Two-dimensional models of composites with a linear-elastic, homogenous and isotropic matrix were considered. The BEM computer code has simple structure and requires division of external boundaries and fibres into boundary elements. Because displacements and tractions are interpolated only along the boundaries, the results are very accurate. The method allows very simple modification of positions, orientations and lengths of the fibres. This feature is very important in the homogenization of composites with randomly distributed fibres, which requires the analysis of many different microstructures in order to obtain statistically representative effective elastic properties. Three numerical examples were solved using the developed computer code. The first simple numerical example—a rigid fibre in a circular disc, shows the influence of fibre length on displacements and high accuracy of the method. The second numerical example—parallel rigid fibres in a square plate, demonstrates the influence of orientation of uniformly distributed fibres on effective properties. As might be expected, the largest Young modulus is for fibres oriented in the direction of the applied tensile loading. In this case, the Poisson ratio and the Kirchhoff modulus of the composite and the matrix have the same values. For a certain orientation, the fibres do not affect the Young modulus. The maximum of the Poisson ratio, the Kirchhoff moduli and shear-extension coupling coefficients are for fibres inclined with respect to the edges of the representative volume element. The third example—randomly distributed fibres in a square plate, gives statistically representative effective properties. The average effective properties for randomly distributed fibres are lower than for uniformly distributed parallel fibres at a specific angle. As the result of the homogenization of the composite material with randomly distributed parallel fibres, the homogenous orthotropic material has been obtained. The same homogenization procedure applied to composites with randomly distributed and oriented fibres gives the homogenous isotropic material.