On kinematic and self-excited rail vehicle–track interaction

Abstract

The paper contains description of dynamical problems connected with the self-excitation and kinematic excitation of rail vehicle and railway track. Some phenomena are presented which may create high loads resulting in track degradation and fatigue of wheelset axles. An alternative approach to rail vehicle hunting is proposed. Examples of experimental investigations are given which show that the dynamical load acting on the track can be much higher than the static load.

1 Introduction

The dynamic interaction of a rail vehicle with its track is a very complex phenomenon. Some effects are still not well understood even by specialists in this field. A wide palette of models is required to cover the variety of different aspects of the topic. The majority of experimental observations made on real vehicle–track systems can be explained using theoretical analyses and numerical investigations. Their results may help the designers of railway vehicles to increase the safety and comfort of travel and to reduce the maintenance costs of tracks and trains. A study of some selected problems concerning the influence of system parameters on the stability of a track–train system in relative motion is presented in the following study.

2 Hunting as a classic train–track instability of two subsystems in relative motion

Hunting in the railway dynamics is known as a transverse instability and lateral vibration of wheelsets and the whole train structure. The explanation of hunting is connected with the conical shape of railway wheels. A classic theory of hunting can be found in [1]. The idea of such a model is shown in Fig. 1, and an exemplary time flow of lateral hunting vibration is presented in Fig. 2.

Fig. 1

Conical shape of railway wheels as the reason of wheelset hunting

Fig. 2

Wheelset hunting angle ($\alpha$) and lateral displacement y versus time (t)

In the following, another reason and model of train sinusoidal motion (hunting) are presented. It is more general than the usual models and can be applied also for magnetic levitated trains (MAGLEV).

Let us consider a classic train–track system or a MAGLEV train composed of two continuous subsystems interacting by massless elastic layers of distributed stiffness $c_{0}$. We assume that the train of transverse bending stiffness $E_{0} I_{0}$ and linear mass density $\mu _{0}$ is moving with constant traction speed $U_{0}$ along the track of stiffness $E_{1} I_{1}$ and mass density $\mu _{1}$ which in turn is transversely supported by an elastic layer, modeled as Winkler foundation of stiffness $c_{1}$, as shown in Fig. 3.

Fig. 3

Two continuous subsystems modeling the train–track interaction

The equations of transverse motion of the above system are as follows:

$$\begin{aligned} E_{1} I_{1} w_{,xxxx} +\mu _{1} w_{,tt} +c_{0} (w-y)=0, \end{aligned}$$

(1)

$$\begin{aligned} E_{0} I_{0} y_{,xxxx} +\mu _{0} \left( {y_{,tt} -2U_{0} y_{,xt} +U_{0}^{2} y_{,xx} } \right) +c_0 (y-w)=0. \end{aligned}$$

(2a)

where x denotes longitudinal coordinate ($x=x_1$) and w and y are lateral displacements (in direction of $x_2$), respectively.

The second case of the train modeling is connected with the case of train bending stiffness equal to zero ($E_{0}I_{0}=0$), which changes the beam into a set of oscillators shown in Fig. 4.

Fig. 4

Model of train–track interaction with train stiffness neglected

Equation (2a) for the system with zero train bending stiffness takes the form:

$$\begin{aligned} \mu _0 \left( {y_{,tt} -2U_0 y_{,xt} +U_0^2 y_{,xx} } \right) +c_0 (y-w)=0 \end{aligned}$$

(2b)

After fulfilling the equations of motion by the following solution in the form of traveling waves:

$$\begin{aligned} w(x,t)=A\hbox {e}^{ik(x-vt)},\quad \hbox {y} (x,t)=B\hbox {e}^{ik(x-vt)} \end{aligned}$$

(3)

we obtain the following characteristic equation which is qualitatively similar to that derived in [2]:

$$\begin{aligned} \left( {\left( {S^{2}-v^{2}} \right) +\alpha ^{2}} \right) \left( {b\alpha ^{2}-v_0^2 } \right) -b\alpha ^{4}=0 \end{aligned}$$

(4)

where $v_{0} =v-U_{0}$, $S^{2}=\left( {E_{1} I_{1} k^{2}+c_{1} /k^{2}} \right) /\mu _{1}$, $b=\mu _{1} /\mu _0$, $\alpha ^{2}=c_{0} /\mu _{1} k^{2}$, k is wave number and v denotes wave phase velocity.

In case of four real roots v of Eq. (4) for real value of $U_{0}$, the motion is stable. In case of two real roots, the other two are complex conjugate described by expression (5).

$$\begin{aligned} v_{1,2} =v^{{*}}\pm \hbox {i}\varepsilon \end{aligned}$$

(5)

where $v^{{*}}\;\mathrm{{and}}\;\varepsilon$ are real numbers dependent on train speed $U_0$.

In this case, the lateral motion is unstable because at least one of the roots (5) describes increasing solution in time, [3]. Use of Eq. (4) allows one to determine the critical speeds which constitute the boundaries of unstable harmonic motion on ($v,U_{0}$) plane, as shown in Fig. 5.

Fig. 5

Qualitative view of the ($v,U_0$) plane with critical speeds as boundaries of instability

In the real case, we can observe phenomena showing train instability like hunting, which has a limit cycle. In reality, the hunting amplitude is limited by nonlinearities occurring in real systems. To the problem of a nonlinear analysis of hunting as a self-excited vibration, we will devote a separate paper.

3 Wheel–rail self-excited vibration

The next case under consideration is devoted to the friction-induced vibration which is the reason of serious damages of tracks and wheelsets, such as corrugation, sleep waves, axle fatigue as a result of wheelset self-excitation (scheme is shown in Fig. 6). The right-hand part of Fig. 6 contains relatively simple (reversible) relations of the friction force (f) vs. creepage (s) with a decreasing part of characteristics leading to what is called negative damping. Such a model is commonly used in the literature (see [1]).

Fig. 6

Scheme of wheelset–track self-excited vibration and the model of fiction–friction force, f, versus creepage, s

The famous tragic catastrophe of the ICE 3 train at line Köln-Düsseldorf in 2008 was a results of wheelset axle fatigue due to friction-induced torsional vibration with frequency of ca 100Hz [4]. The broken axle of that ICE 3 train is shown in Fig. 7.

Fig. 7

Broken axle of ICE 3 at line Köln-Düsseldorf (Germany) in 2008 [4]

The problem was intensively studied during the last few years. The main problem is related to extremely quick recognition of initiation of self-excitation process and making as short as possible the time gap $\Delta {t}$ until the control system changes the driving moment [4, 5]. Time $\Delta {t}$ (see Fig. 8) in case of electric drive is relatively short, but in case of diesel motor drive is much longer which makes the number of wheelset torsional oscillations much greater (fatigue). Another possibility to overcome the above problem can be application of dampers, dynamic vibration absorber or additional vibration intentionally induced, as shown in Sect. 4.

Fig. 8

Self-excited wheelset vibration with marked time of recognition of self-excitation and time delay $\Delta {t}$ till control system changes the driving moment

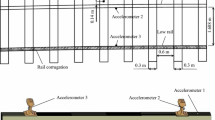
Another effect of friction-induced vibration is slip waves occurring on the low rail of a curved track as was pointed out experimentally by DB AG/ÖBB/SBB experts in Brixental (Fig. 9) and confirmed during simulation [5, 6].

Fig. 9

View of the track on the bridge in Brixental between Westendorf and Hopfgarten (Austria)

An interesting phenomenon was observed that on a long curved track the sleep waves were regular with a typical wave length and amplitude, except the short part on the bridge where the amplitudes of wavy shape of rails were a few times smaller than those out of bridge. Slip waves on a rail are shown in Fig. 10.

Fig. 10

Corrugations on a rail called slip waves [7]

The above question was explained during investigation of influence of the vibration external excitation on friction self-excited mechanical system [6]. It was pointed out using relatively complicated friction model dependent on the process history that it is possible to limit the self-excitation by means of additional vibrational excitation. Comparing the results, one can conclude that vibration of the bridge excited by the train can reduce the sleep waves in the rails.

Now we are going to explain the phenomena of reducing the self-excited vibration by means of an additional vibration (without phase control). Model of the system being used to identify the friction law is shown in Fig. 11.

Fig. 11

Scheme of mechanical system with friction

The system shown in Fig. 11 is described by the following equation of motion:

$$\begin{aligned} \ddot{x}+\left( {d_1 +d_2 } \right) \dot{x}+x=f\left( {w,t_s ,\delta ,sgn(w)} \right) \end{aligned}$$

(6)

where the notations are:

• $x=KX/F_0$—dimensionless displacement,

• K—spring stiffness,

• $F_0$—constant normal reaction,

• $d_1 ,d_2$—internal and external viscous damping, respectively,

• $w=s-\dot{x},$—relative velocity,

• $t_s$—time of sticking,

• $\delta =\mathrm{d}f_s /\mathrm{d}t$—force rate.

The experimental method of investigation and the results of measurements of the friction force as a function of ($t_{s}$, $\delta$) are given in [5]. For each linear part of the model, it is possible to obtain analytically the exact solution. Successive tailoring of the particular parts of solution leads to the whole process in time. At the first part of the stick–slip characteristic, we observe increase in the force associated with damping. After reaching maximum force of friction, the system becomes self-excited on the two parts of characteristic curve shown in Fig. 12, until the speed reaches its maximum. The change of acceleration sign is connected with further decreasing force associated with the positive damping. At the end of this part of characteristic, we have the sticking (Fig. 12) and the process is continued with increasing friction force at sticking.

The crucial points are connected with initiation of sliding which depends on the force rate and time of sticking (experimentally measured in [6]). Than we observe increase in the force associated with damping, after reaching maximal force the system is self-excited till the speed reach maximum value. The change of acceleration sign is connected with further decreasing force and positive damping. On the end of this part of characteristic, we obtain sticking or rapidly increasing frictional force and the process is further continued.

We will present an example using a history-dependent friction model and exemplary numerical results. The nonclassic, history-dependent model of friction used in simulation was assumed to be piecewise linearly dependent on the relative speed (creepage), force rate, time of sticking and sign of acceleration (arrows in Fig. 12 show the direction of the process running) [6]. In the piecewise linear model, we can easily mark parts of damping ($d>0$) and parts of excitation ($d<0$).

Fig. 12

Dynamic characteristic of the friction model depended on the process history for stick–slip vibration

Fig. 13

Scheme of friction model depended on the process history for semi-harmonic vibration

In case of higher slip velocities, the sticking does not occur and we are faced with motion called semi-harmonic vibration. The corresponding friction characteristic is shown in Fig. 13.

4 Self-excited system subjected to additional vibration

To explain the phenomena, let us consider a system shown in Fig. 11, which is a simplification of that shown in the left side of Fig. 6. We will give an example that using additional harmonic excitation limitation of vibration amplitude is possible. Instead of constant speed S (dimensionless $s = S (\textit{KM})^{0.5}/F_{0}$), we assume that s has an additional harmonic excitation $\Delta {s}$,

$$\begin{aligned} s_h =s+\Delta s,\Delta s=u_0 \cos \eta t+d_1 u_0 \eta \sin \eta t \end{aligned}$$

(7)

Thus, equation of motion (6) takes the form

$$\begin{aligned} \ddot{x}+\left( {d_1 +d_2 } \right) \dot{x}+x=f\left( {w,t_s ,\delta ,sgn(w)} \right) +u_0 \cos \eta t+d_1 u_0 \eta \sin \eta t \end{aligned}$$

(8)

To illustrate the phenomenon of limitation of self-excited vibration amplitude, we present the results of simulations for the particular data: slip velocity $s=0.2$, amplitude of additional vibration $u_{0}= 0.2$ and two values of frequency $\eta$, very close to each other $\eta _a =0.212$ and $\eta _b =0.213$.

Fig. 14

Two qualitatively different types of solution for the system with additional external harmonic excitation. Example of two slightly different excitation frequencies

Fig. 15

Displacement–velocity phase plane for two qualitatively different types of solution for the system with additional external harmonic excitation of two slightly different frequencies

It is visible in Fig. 14 that the solution consists of vibration of two frequencies. The first one is connected with self-excitation and the second one with additional excitation. Increasing slightly the frequency of the additional excitation $\eta$ (<0.5%), the response after a few cycles changes qualitatively to that of amplitude about three times smaller than the previous one. The change is visible in the right-hand side graph in Fig. 14. Such a change (after a few cycles) is possible only in case of a history-dependent model of friction. The displacement–velocity phase plane portraits for the above-mentioned two kinds of solutions are shown in Fig. 15. The graphs are qualitatively different although the frequencies are very close to each other.

Talking about additional vibrational excitation on the bridge, we can supplement the above study and mention a few kinds of kinematic excitation of rail vehicles. As the source of such excitation, we can mention: periodically spaced corrugation, periodically spaced sleepers, supports of estacade and the out-of-round railway wheels (wheel polygonalization) creating also a kind of periodic kinematic excitation.

As a source of similar excitation, we can mention: periodically spaced corrugation, periodically spaced sleepers, supports of estacades and wheels poligonalization (the out-of-round railway wheels). The above phenomena, similarly as the earlier mentioned sleep waves on the Brixental bridge, can generate a periodic kinematic excitation.

The kinematically excited vibration can be solved using Floquet’s theory and looking for a traveling wave form of the solution. Contrary to a wavy form of interaction between two continuous systems (Fig. 2), in the case of train modeled as lumped system the problem of traveling and oscillating concentrated load (force) acting on a beam must be solved. Such a problem was formulated by Mathews [8] who proposed the solution in the form of standing waves. In that paper, the boundary conditions were not properly formulated, particularly the condition of radiation. The traveling wave solution with correct formulation of the boundary conditions allows to solve the problem taking into account the group velocity of generated waves. The proper solution was given in 1986 by Bogacz and Krzyżyński [9]. Such a solution allows us to solve various problems of discrete dynamical interaction of the train as a lumped system with a track modeled as continuous systems. As the practical example of the theory application, we can call the train–track dynamical interaction and its stability.

5 Concluding remarks

A study of selected problems of vehicle–track interaction concerning the influence of hybrid and continuous modeling on the stability and self-excitation of systems in relative motion is given. An alternative approach to the classic rail vehicles hunting [10], based on instability of two continuous, one-dimensional systems in relative motion is proposed. The presented results extend our previous considerations presented in [3, 11] and in [12]. The case devoted to the friction-induced vibration which is the reason of many damages of trains and tracks was considered. It was shown that an additional vibrational excitation of proper frequency can reduce the friction-induced vibration and its negative consequences for the train and track structure.