Abstract
We explore the utility of strain-controlled large amplitude oscillatory shear (LAOS) deformation for identifying and characterizing apparent yield stress responses in elastoviscoplastic materials. Our approach emphasizes the visual representation of the LAOS stress response within the framework of Lissajous curves with strain, strain rate, and stress as the coordinate axes, in conjunction with quantitative analysis of the corresponding limit cycle behavior. This approach enables us to explore how the material properties characterizing the yielding response depend on both strain amplitude and frequency of deformation. Canonical constitutive models (including the purely viscous Carreau model and the elastic Bingham model) are used to illustrate the characteristic features of pseudoplastic and elastoplastic material responses under large amplitude oscillatory shear. A new parameter, the perfect plastic dissipation ratio, is introduced for uniquely identifying plastic behavior. Experimental results are presented for two complex fluids, a pseudoplastic shear-thinning xanthan gum solution and an elastoviscoplastic invert-emulsion drilling fluid. The LAOS test protocols and the associated material measures provide a rheological fingerprint of the yielding behavior of a complex fluid that can be compactly represented within the domain of a Pipkin diagram defined by the amplitude and timescale of deformation.












Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Notes
The terms elastic, viscous, and plastic are sometimes used to refer to specific components of constitutive equations, but here the term elastoviscoplastic is used to refer to experimentally measured material responses as described in the text.
References
API (2009) Recommended practice for laboratory testing of drilling fluids, American Petroleum Institute. API RP 13I
Atalik K, Keunings R (2004) On the occurrence of even harmonics in the shear stress response of viscoelastic fluids in large amplitude oscillatory shear. J Non-Newton Fluid Mech 122(1–3):107–116
Barnes HA (1999) The yield stress - a review or ‘pi alpha nu tau alpha rho epsilon iota’ - everything flows? J Non-Newton Fluid Mech 81(1–2):133–178
Barnes HA, Walters K (1985) The yield stress myth. Rheol Acta 24(4):323–326
Bird RB, Dai GC, Yarusso BJ (1983) The rheology and flow of viscoplastic materials. Rev Chem Eng 1(1):1–70
Bird R, Armstrong R, Hassager O (1987) Dynamics of polymeric liquids: volume 1 fluid mechanics. John Wiley & Sons, Inc, New York
Brunn PO, Asoud H (2002) Analysis of shear rheometry of yield stress materials and apparent yield stress materials. Rheol Acta 41(6):524–531
Cho KS, Ahn KH, Lee SJ (2005) A geometrical interpretation of large amplitude oscillatory shear response. J Rheol 49(3):747–758
Cross MM (1965) Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic systems. J Colloid Sci 20(5):417–437
Dealy JM, Wissbrun KF (1990) Melt rheology and its role in plastics processing: theory and applications. Van Nostrand Reinhold, New York
Debbaut B, Burhin H (2002) Large amplitude oscillatory shear and Fourier-transform rheology for a high-density polyethylene: Experiments and numerical simulation. J Rheol 46(5):1155–1176
Doraiswamy D, Mujumdar AN, Tsao I, Beris AN, Danforth SC, Metzner AB (1991) The Cox–Merz rule extended - a rheological model for concentrated suspensions and other materials with a yield stress. J Rheol 35(4):647–685
Ewoldt RH, McKinley GH (2009) On secondary loops in LAOS via self-intersection of Lissajous-Bowditch curves. Rheol Acta. doi:10.1007/s00397-009-0408-2
Ewoldt RH, Winter P, McKinley GH (2007) MITlaos version 2.1 Beta for MATLAB. Cambridge, MA, self-published
Ewoldt RH, Hosoi AE, McKinley GH (2008) New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J Rheol 52(6):1427–1458
Fischer C, Plummer CJG, Michaud V, Bourban PE, Manson JAE (2007) Pre- and post-transition behavior of shear-thickening fluids in oscillating shear. Rheol Acta 46(8):1099–1108
Ganeriwala SN, Rotz CA (1987) Fourier-transform mechanical analysis for determining the nonlinear viscoelastic properties of polymers. Polym Eng Sci 27(2):165–178
Graham MD (1995) Wall slip and the nonlinear dynamics of large-amplitude oscillatory shear flows. J Rheol 39(4):697–712
Harris J, Bogie K (1967) The experimental analysis of non-linear waves in mechanical systems. Rheol Acta 6(1):3–5
Hyun K, Wilhelm M (2009) Establishing a new mechanical nonlinear coefficient Q from FT-rheology: first investigation of entangled linear and comb polymer model systems. Macromolecules 42(1):411–422
Hyun K, Kim SH, Ahn KH, Lee SJ (2002) Large amplitude oscillatory shear as a way to classify the complex fluids. J Non-Newton Fluid Mech 107(1–3):51–65
Jeyaseelan RS, Giacomin AJ (2008) Network theory for polymer solutions in large amplitude oscillatory shear. J Non-Newton Fluid Mech 148(1–3):24–32
Klein C, Spiess HW, Calin A, Balan C, Wilhelm M (2007) Separation of the nonlinear oscillatory response into a superposition of linear, strain hardening, strain softening, and wall slip response. Macromolecules 40(12):4250–4259
Macosko CW (1994) Rheology: principles, measurements, and applications. Wiley-VCH, New York, p 218
Macsporran WC, Spiers RP (1982) The dynamic performance of the Weissenberg rheogoniometer. 2. large-amplitude oscillatory shearing - fundamental response. Rheol Acta 21(2):193–200
Macsporran WC, Spiers RP (1984) The dynamic performance of the Weissenberg rheogoniometer. 3. large-amplitude oscillatory shearing - harmonic analysis. Rheol Acta 23(1):90–97
Maxey J (2007) Thixotropy and yield stress behavior in drilling fluids. AADE 2007 Drilling Fluids Conference (AADE-07-NTCE-37)
Mitsoulis E (2007) Flows of viscoplastic materials: models and computations. In: Binding DM, Hudson NE, Keunings R (eds) Rheology reviews 2007. Glasgow, Universities Design & Print, pp 135–178
Mujumdar A, Beris AN, Metzner AB (2002) Transient phenomena in thixotropic systems. J Non-Newton Fluid Mech 102(2):157–178
Papanastasiou TC (1987) Flows of materials with yield. J Rheol 31(5):385–404
Philippoff W (1966) Vibrational measurements with large amplitudes. Trans Soc Rheol 10(1):317–334
Pipkin AC (1972) Lectures on viscoelasticity theory. Springer, New York
Rouyer F, Cohen-Addad S, Höhler R, Sollich P, Fielding SM (2008) The large amplitude oscillatory strain response of aqueous foam: strain localization and full stress Fourier spectrum. Eur Phys J E 27(3):309–321
Saramito P (2007) A new constitutive equation for elastoviscoplastic fluid flows. J Non-Newton Fluid Mech 145(1):1–14
Stadler FJ, Leygue A, Burhin H, Bailly C (2008) The potential of large amplitude oscillatory shear to gain an insight into the long-chain branching structure of polymers. The 235th ACS National Meeting, vol 49, New Orleans, LA, U.S.A., Polymer Preprints ACS, pp 121–122
Tee TT, Dealy JM (1975) Nonlinear viscoelasticity of polymer melts. Trans Soc Rheol 19(4):595–615
Ugural AC, Fenster SK (2003) Advanced strength and applied elasticity. Prentice Hall, Upper Saddle River, NJ
van Dusschoten D, Wilhelm M (2001) Increased torque transducer sensitivity via oversampling. Rheol Acta 40(4):395–399
Wilhelm M (2002) Fourier-Transform rheology. Macromol Mater Eng 287(2):83–105
Wilhelm M, Reinheimer P, Ortseifer M (1999) High sensitivity Fourier-transform rheology. Rheol Acta 38(4):349–356
Yoshimura AS, Prudhomme RK (1987) Response of an elastic Bingham fluid to oscillatory shear. Rheol Acta 26(5):428–436
Yoshimura AS, Prudhomme RK (1988) Wall slip effects on dynamic oscillatory measurements. J Rheol 32(6):575–584
Yu W, Wang P, Zhou C (2009) General stress decomposition in nonlinear oscillatory shear flow. J Rheol 53(1):215–238
Acknowledgements
This work was supported in part by a gift from Procter & Gamble (Cincinnati, OH). R.H.E. gratefully acknowledges funding from the National Science Foundation Graduate Research Fellowship Program and the DARPA Chemical Robots program.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Raw data from LAOS experiments
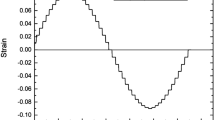
The full LAOS response of the xanthan gum, including transients, is shown in Fig. 13. The Lissajous curves of the raw measured stress vs. strain indicate an initial transient response which quickly settles into steady oscillatory orbits.
Raw LAOS data for the xanthan gum solution (0.2 wt.% aqueous). Individual orbits are Lissajous curves of normalized stress vs. strain. The initial condition at the beginning of each test is γ = 0, σ = 0. Each individual plot is positioned within a Pipkin space according to the associated LAOS input parameters {ω, γ 0}. The peak stress within each cycle (including the initial transient) is indicated above the individual curves
The drilling fluid LAOS response is shown in Fig. 14. Lissajous curves of apparent stress vs. rim shear rate are arranged within a Pipkin space according to the LAOS input conditions {ω, γ 0}. The startup transients settle into steady oscillations, which are used for the quantitative LAOS analysis presented here.
Experimental LAOS data for the drilling fluid, including transients, shown as normalized Lissajous curves of stress vs. strain. The maximum absolute value of stress is shown above each curve. The test sequence consists of strain-amplitude sweeps (γ 0 = 0.0056–10) at constant frequency, in the order ω = (15, 4.75, 1.5, 0.475) rad s − 1. The total number of cycles for each frequency is N = (19, 12, 20, 12) cycles for ω = (15, 4.75, 1.5, 0.475) rad s − 1, respectively. The approach to the final periodic orbit can be identified visually. The data shown in Fig. 1 correspond to the test shown here at ω = 15 rad s − 1, γ 0 = 3.16. The final six steady oscillatory cycles are used for quantitative analysis of the limit cycle behavior
Both materials settle into steady oscillations which have the expected symmetry for shear-symmetric responses, i.e., any curve can be rotated by 180° about an axis out of the page and result in the same steady oscillatory curve. This corresponds to the existence of only odd harmonics in the Chebyshev/Fourier representation, Eq. 6.
Interpolation method used for Pipkin space fingerprints
To improve visualization of trends and contour lines in the rheological fingerprints, the data are interpolated to produce smooth gradients, as in Fig. 15b. The figures presented here have been interpolated to include 100 points per decade in both frequency ω and strain amplitude γ 0. The collection of experimental data occurs at discrete values within the Pipkin space of {ω, γ 0}. For example, the drilling fluid data is spaced at two points per decade in frequency ω and four points per decade in strain amplitude γ 0. The viscoelastic parameters corresponding to these discrete sampling points can be visualized by plots such as Fig. 15a. Color blocks are used for this plot, which are centered about the imposed values of {ω, γ 0}. The width and height of the block area is determined by the spacing of the data. The finite width and height of each block increases the limits of the plot beyond where data was actually collected, since the blocks are centered over the corresponding {ω, γ 0} location. Only four strain sweeps (at different fixed frequency) were used to create this fingerprint.
Rights and permissions
About this article
Cite this article
Ewoldt, R.H., Winter, P., Maxey, J. et al. Large amplitude oscillatory shear of pseudoplastic and elastoviscoplastic materials. Rheol Acta 49, 191–212 (2010). https://doi.org/10.1007/s00397-009-0403-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00397-009-0403-7