Skip to main content
Springer Nature Link
Log in

A shear rheometer for measuring shear stress and both normal stress differences in polymer melts simultaneously: the MTR 25

  • Original Contribution
  • Published:
Rheologica Acta Aims and scope Submit manuscript

Abstract

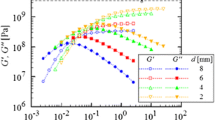
The MTR 25 is a multitask rheometer (for shear and squeeze flow) with 25 kg of normal force and a partitioned plate. Torque and normal force are measured at both, the inner disk and the outer ring of the plate. The first and second normal stress differences can be determined from a single test. The axial stiffness is high (107 N/m) by using rigid springs and strain gauges for the load cell. Monodisperse polystyrene (M w = 206 kg/mol, 180°C) has been sheared in the range from 0.05 to 47 s − 1. The viscosity and first normal stress difference are highly reproducible. The second normal stress difference scatters and mirrors the instability at the rim. A critical comparison is made between the MTR 25 method and the single transducer evaluation method (RMS 800 method, Schweizer, Rheol Acta 41:337–344, 2002): Both yield excellent and coinciding viscosity and first normal stress difference data. The RMS 800 method gives more stable second normal stress difference data, since the normal force from the outer ring, which is influenced by edge fracture, is not used. Data for the RMS 800 method can be acquired on the MTR 25. The high normal force capacity permits larger samples and higher shear rates than on the RMS 800.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Notes

  1. Rheometrics Mechanical Spectrometer, manufactured by Rheometric Scientific with a force rebalance transducer for torque and normal force (up to 20 N). Electrical heating fitted (Meissner et al. 1989).

  2. The design of a low load rheometer is equally challenging. Since normal forces decrease quadratically with rate, the temperature must be well controlled to get a perfectly stable baseline. Such requirements can only be obtained with electrically temperature control, but not with convection ovens. The ARES, e.g., can keep temperature constant within ±0.05°C at a level of 200°C, which is far too noisy to even explore the full range of its force rebalance transducer.

  3. Maxon EC motor, Type 276575 with tacho generator.

  4. Manufacturer HBM, Type 1-LC11-3/350, resistance 350 Ω each.

  5. MGCplus AB22A from Hottinger Baldwin Messtechnik, Darmstadt, Germany.

  6. Manufacturer HBM, Type 1-XG21-6/350, resistance 350 Ω each.

  7. ARES LR2, manufactured by TA Instruments, Eschborn, Germany, with a force rebalance transducer and a maximal normal force of 20 N. Temperature control by a convection oven

  8. Registered Mark, version 7.1

  9. Manufactured by Anton Paar, Ostfildern, Germany, with directly electrically heated plate and radiation heating for the cone.

  10. A direct implication for the experiments is that for the signal F o to be strong enough, the sample radius R should be typically R > 1.25·R i. For the RMS 800 method (considering F i only), this restriction does not exist.

References

  • Adams N, Lodge AS (1964) Rheological properties of concentrated polymer solutions II. A cone-and-plate and parallel plate pressure distribution apparatus for determining normal stress differences in steady shear flow. Philos Trans R Soc Lond, A 256(1068):149–184

    Article  CAS  Google Scholar 

  • Attané P, Pierrard JM, Turrel G (1985) Steady and transient shear flows of polystyrene solutions II: shear-rate dependence of non-dimensional viscometric functions: characteristic relaxation times. J Non-Newton Fluid Mech 18:319–333

    Article  Google Scholar 

  • Dutcher CS, Venerus DC (2007) Compliance effects on the torsional flow of a viscoelastic fluid. J Non-Newton Fluid Mech 150(2–3):154–161

    Google Scholar 

  • Fetters LJ, Lohse DJ, Graessley WW (1999) Chain dimensions and entanglement spacings in dense macromolecular systems. J Polymer Sci, Part B, Polym Phys 37:1023–1033

    Article  CAS  Google Scholar 

  • Hansen MG, Nazem F (1975) Transient normal force transducer response in a modified Weissenberg Rheogoniometer. Trans Soc Rheol 19(1):21–36

    Article  Google Scholar 

  • Jobling A, Roberts JE (1959) Flow testing of viscoelastic materials. Design and calibration of the Roberts–Weissenberg model R8 Rheogoniometer. J Polym Sci 36:421–431

    Article  CAS  Google Scholar 

  • Kalogrianitis SG, van Egmond JW (1997) Full tensor optical rheometry of polymer fluids. J Rheol 41(2):343–364

    Article  CAS  Google Scholar 

  • Kaye A, Lodge AS, Vale DG (1968) Determination of normal stress differences in steady shear flow. II. Flow birefringence, viscosity, and normal stress data for a polyisobutylene liquid. Rheol Acta 7(4):368–379

    Article  CAS  Google Scholar 

  • Magda JJ, Baek SG (1994) Concentrated entangled and semidilute entangled polystyrene solutions and the second normal stress difference. Polymer 35(6):1187–1194

    Article  CAS  Google Scholar 

  • Meissner J (1972) Modification of the Weissenberg Rheogoniometer for measurement of transient rheological properties of molten polyethylene under shear. Comparison with tensile data. J Appl Polym Sci 16:2877–2899

    Article  CAS  Google Scholar 

  • Meissner J, Garbella RW, Hostettler J (1989) Measuring normal stress differences in polymer melt shear flow. J Rheol 33(6):843–864

    Article  CAS  Google Scholar 

  • Neergaard J, Park K, Venerus DC, Schieber J (2000) Exponential shear flow of linear, entangled polymeric liquids. J Rheol 44(5):1043–1054

    Article  CAS  Google Scholar 

  • Ohl N, Gleissle W (1992) The second normal stress difference for pure and highly filled viscoelastic fluids. Rheol Acta 31:294–305

    Article  CAS  Google Scholar 

  • Pollett WFO (1955) Rheological behaviour of continuously sheared polyethylene. Br J Appl Phys 6:199–206

    Article  Google Scholar 

  • Schweizer T (2002) Measurement of the first and second normal stress differences in a polystyrene melt with a cone and partitioned plate tool. Rheol Acta 41:337–344

    Article  CAS  Google Scholar 

  • Schweizer T (2004) A quick guide to better viscosity measurements of highly viscous fluids. Appl Rheol 14(4):197–201

    Google Scholar 

  • Schweizer T, Bardow A (2006) The role of instrument compliance in normal force measurements of polymer melts. Rheol Acta 45(4):393–402

    Article  CAS  Google Scholar 

  • Schweizer T, Stöckli M (2008) Departure from linear velocity profile during shear of polystyrene melts in cone–plate geometry. J Rheol 52(3):713–727

    Article  CAS  Google Scholar 

  • Schweizer T, van Meerveld J, Öttinger HC (2004) Nonlinear shear rheology of polystyrene melt with narrow molecular weight distribution—experiment and theory. J Rheol 48(6):1345–1363

    Article  CAS  Google Scholar 

  • Venerus DC (2007) Free surface effects on normal stress measurements in cone and plate flow. Appl Rheol 17:36494-1–36494-6

    Google Scholar 

  • Winter HH (1997) Analysis of dynamic mechanical data: inversion into a relaxation time spectrum and consistency check. J Non-Newton Fluid Mech 68:225–239

    Article  CAS  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Prof. Hans Christian Öttinger for providing from theory the motivation for N2 measurements. The rheometer could not have been successfully built without the experience from Prof. Joachim Meissner’s partitioned plate on the RMS 800, which finally proved the versatility of the technique. J.M. and Clarisse Luap are thanked for their critical comments on the paper. Frank Moszner and Moritz Küng helped to perform test measurements on the instrument. Finally, the ETH Zürich is acknowledged for funding the construction of the rheometer.

Author information

Authors and Affiliations

  1. Department of Materials, Institute of Polymers, ETH Zürich, 8093, Zurich, Switzerland

    Thomas Schweizer, Jürg Hostettler & Fredy Mettler

Authors
  1. Thomas Schweizer
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jürg Hostettler
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Fredy Mettler
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Thomas Schweizer.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Schweizer, T., Hostettler, J. & Mettler, F. A shear rheometer for measuring shear stress and both normal stress differences in polymer melts simultaneously: the MTR 25. Rheol Acta 47, 943–957 (2008). https://doi.org/10.1007/s00397-008-0300-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00397-008-0300-5

Keywords