Introduction

Efficient compatibilization of immiscible polymer blends is one of the most important tasks in polymer material science. It was found that block copolymers with blocks that are identical to, miscible with, or adhere to related components of polymer blends are proper compatibilizers [1,2,3,4]. Block copolymers are mostly substantially more expensive than compatibilized homopolymers, and therefore, the choice of the most efficient compatibilizer is of great practical importance. Results of experimental studies indicate that the effect of a copolymer on the equilibrium interfacial tension of a blend correlates quite well with its effect on the blend phase structure and mechanical properties in spite of the fact that the whole effect of a copolymer is complex [3,4,5,6,7,8,9,10,11].

Numerous studies have paid attention to the theoretical prediction of the effect of block copolymers on the interfacial tension in immiscible polymer blends. Their results are summarized and discussed in [4, 6, 12, 13]. Leibler’s theory [14], comparing the chemical potential of a copolymer in the interfacial brush with that in the blend bulk phases, is frequently used for the calculation of the effect of block copolymers on the interfacial tension in strongly immiscible polymer blends. Noolandi [15] pointed out that Leibler’s theory neglected the main contribution to the reduction of the interfacial tension, which is of enthalpic and not entropic origin. The author proposed that the interfacial tension between neat homopolymers should be substituted by the interfacial tension, calculated by Noolandi and Hong using mean field theory [16] by means of the expression for the free energy of the interfacial film. Retsos et al. [17, 18] and Anastasiadis [12] pointed out that Leibler’s expression could be corrected by adding the entropy of localization of the blocks introduced by Shull and Kramer [19].

It has been shown in our previous papers [6, 20] that none of the approximations used to calculate the interfacial tension in polymer blends containing a compatibilizer is applicable to polymer blends having a fine phase structure. These approximations used an assumption that the localization of block copolymers at the interface had a negligible effect on their concentration in bulk phases, or that a whole amount of the added copolymer was localized at the interface. Using the original Leibler’s expression [14] for the free energy of the interfacial film and the expression corrected according to Retsos et al. [17, 18] and Anastasiadis [12], a distribution of a copolymer between the interface and bulk phases as well as an interfacial tension in compatibilized polymer blends were determined [6, 20]. A new method of calculation of the copolymer fraction at the interface, avoiding the necessity of the approximations leading to the expressions for a dry or wet brush system, was proposed in our latest paper [21]. In this paper, we also compared the distribution of a copolymer between the interface and bulk phases and a decrease in the interfacial tension calculated using the original Leibler expressions as well as its modification according to refs. [12, 17, 18].

However, the comparison of the correction of the interfacial tension following from the addition of the entropy of localization [12, 17, 18] with the expression for the blend interfacial tension proposed by Noolandi [15] shows that the so far used correction does not reflect all contributions to the blend interfacial tension. Therefore, we have decided to compare the results obtained from the original Leibler’s theory, its modification with heretofore used correction, and with its modification using the blend interfacial tension proposed by Noolandi [15]. For simplicity, Noolandi’s expression for the blend interfacial tension was derived for a symmetric system with the same volume fractions of homopolymers, the same lengths of copolymer blocks, and a very large length of both homopolymers. We try to generalize it for systems having different lengths of copolymer blocks and volume fractions of homopolymers using its derivation in ref. [16]. It is necessary to elucidate the relations between models of a blend used in ref. [14] and those in [15, 16], as well as between variables in our previous papers [6, 20, 21] and those used in [15, 16].

A model of the studied system is described, and the main equations from previous studies are summarized in the “Model of the system and basic equations” section. The “Expression of Noolandi’s Δγ through the Leibler model parameters” section is focused on the generalization of the Noolandi and Hong equation for a blend having different lengths of copolymer blocks and volume fractions of homopolymers and on relations between variables used in our previous papers [6, 20, 21] and those in the papers of Noolandi [15] and Noolandi and Hong [16]. The calculation methods used are specified in the “Calculation procedure” section. A comparison of the results for localization of a copolymer and a decrease in the interfacial tension calculated according to the original Leibler theory, correction of this theory using the entropy of copolymer localization, and correction of this theory using the interfacial tension derived by Noolandi and Hong [16] are provided in the “Results” section. Conclusions following from the calculation are presented in the “Conclusions” section.

Model of the system and basic equations

We use the model of the system proposed by Leibler [4, 14, 20]. A polymer blend containing homopolymers A consisting of PA and B consisting of PB segments compatibilized with A-B block copolymer where block A consists of NA segments and block B consists of NB segments is considered. The total number of copolymer segments is N = NA + NB. For simplicity, the same length of all segments, a, and their volume, a3, are assumed. The blend contains volume fractions φA, φB, and φAB of the homopolymers A, B, and of the copolymer A-B, respectively. The area of the interface between bulk phases A and B in volume V is S. The fraction of the copolymer \({\varphi }\mathrm{_{AB}^{\left(I\right)}}\) is localized in the interfacial layer consisting of two brushes of thicknesses, LA and LB, respectively. Fractions of the copolymer, \({\varphi }\mathrm{_{AB}^{\left(A\right)}}\) and \({\varphi }\mathrm{_{AB}^{\left(B\right)}}\), are dissolved in the bulk phases A and B, respectively. The amounts of B homopolymer in phase A and of A homopolymer in phase B are negligible for the strongly immiscible A/B blend. The brush of a copolymer at the interface can be swollen with homopolymer A on the side of the phase A (layer with the thickness LA) and with homopolymer B on the side of the phase B. Q with subscripts A, B, and AB denote the number of polymers A, B, and AB in the system, and superscripts (A), (B), and (I) denote the phase, where this number of molecules is localized. Volume fractions and numbers of polymers without superscripts denote their values in the whole system. Concentrations of whole polymer in the bulk phases and on both sides of the interfacial layer are position independent (Flory–Huggins approximation) in the used model.

The following equations for the Gibbs energy of the interfacial film, Ff,L was proposed by Leibler [14]

$${F}_{\mathrm{f,L}}={\gamma }_{0}S+{Q}\mathrm{_{AB}^{\left(I\right)}}\left[{g}_{\mathrm{A}}\left(\mathit\varSigma \right)+{g}_{\mathrm{B}}\left(\mathit\varSigma \right)\right]$$
(1)

where γ0 is the interfacial tension between pure homopolymer phases; Σ is the interfacial area per copolymer joint defined as

$$\mathit{\varSigma} =S/{Q\mathrm{_{AB}^{(I)}}}$$
(2)

and gA and gB represent the Gibbs energy per copolymer block of the A and B brushes in the phases A and B. According to Noolandi [15], Eq. (1) for the Gibbs energy of the interfacial film, Ff should be rewritten as

$${F}_\mathrm{f}=\left({\gamma }_{0}+\Delta \gamma \right)S+{Q}\mathrm{_{AB}^{\left(I\right)}}\left[{g}_\mathrm{A}\left(\mathit\varSigma \right)+{g}_\mathrm{B}\left(\mathit\varSigma \right)\right]$$
(3)

where Δγ is calculated using the mean field theory [15, 16]. According to Retsos et al. [17, 18] and Anastasiadis [12], ΔγR can be expressed as the equation used in our preceding papers [6, 20, 21] and denoted there as Noolandi’s modification

$$\Delta {\gamma }_\mathrm{R}=\frac{kT}{\mathit\varSigma}\mathrm{ln}\frac{2\cdot {6}^\frac{1}{2}{\chi }^\frac{1}{2}\left({L}_\mathrm{A}+{L}_\mathrm{B}\right)}{\pi a}$$
(4)

where k is the Boltzmann constant, T is the temperature, χ is the Flory–Huggins interaction parameter, and π is the Ludolf number.

Determination of Δγ from Nooladi’s mean field theory using variables from our previous papers is object of the following section.

Distribution of a copolymer between the interface and bulk phases can be calculated from equality between the copolymer chemical potential at the interface µI and in the bulk A and B phases (µA, µB) [6, 20, 21]. µI is defined by the equation [6, 14, 21]

$${\mu }_\mathrm{I}={\left(\frac{\partial {F}_\mathrm{f}}{\partial {Q}\mathrm{_{AB}^{\left(I\right)}}}\right)}_{S}$$
(5)

The interfacial tension of the compatibilized system is given by the equation [6, 14, 21]

$$\gamma ={\left(\frac{\partial {F}_\mathrm{f}}{\partial S}\right)}_{{Q}\mathrm{_{AB}^{\left(I\right)}}}$$
(6)

The general dimensionless parameter Γ expressing the interface area to volume ratio was defined in our previous papers [6, 21]

$$\mathit\varGamma =a{S}_{V}/{\varphi }_{\mathrm{A}}\mathrm{where\,}{S}_{V}=S/V$$
(7)

When the phase A forms a system of monodisperse spheres having radius R, Γ = 3a/R. Two dimensionless variables were introduced in our recent paper [21]

$$\mathit\varPsi =\frac{{a}^{2}}{\mathit\varSigma }=\frac{{\varphi }\mathrm{_{AB}^{\left(I\right)}}}{N\mathit\varGamma {\varphi }_\mathrm{A}}$$
(8)

and

$${\mathit\varLambda }_{i}=\frac{{L}_{i}}{a}$$
(9)

Using these variables, equation for gi can be expressed as [21]

$$\frac{{g}_{i}}{kT}=\mathrm{ln}\left( {N}_{i}\mathit\varPsi \right)+\left(\frac{{\mathit\varLambda }_{i}}{\mathit\varPsi {P}_{i}}-\frac{{N}_{i}}{{P}_{i}}\right)\mathrm{ln}\left(1-\frac{{N}_{i}\mathit\varPsi }{{\mathit\varLambda }_{i}}\right)+\frac{3}{2}\frac{{\mathit\varLambda }_{i}^{2}}{{N}_{i}}$$
(10)

Λi is a priori unknown besides Ψ, which should be calculated from the equality of chemical potentials of a copolymer in the interfacial layer and in the bulk phases. Copolymer blocks are unstretched and form the Gaussian coils if concentration of the copolymer at the interface is low. In this case, the thickness of the brush can be characterized by an average end-to-end distance of the copolymer blocks [21].

$${\mathit\varLambda }_{i}={N}_{i}^\frac{1}{2}$$
(11)

A rule when the formulae for low-copolymer concentration, like Eq. (11), should be used is not strictly given. However, we judge that they can be surely applied if unstretched copolymer blocks occupy less area than the full interface area, which means that an area related to a block localized at the interface is larger than the block average quadratic end-to-end distance. In terms of the above-defined symbols, the condition can be expressed as

$$\mathit\varPsi <\frac{1}{{N}_{i}}$$
(12)

while using of symbols from the previous papers [6, 20], the condition is \({\widetilde{\varphi }}\mathrm{_{AB}^{\left(I\right)}}<\frac{N}{{N}_{i}}\mathit\varGamma\). This means \({\widetilde{\varphi }}\mathrm{_{AB}^{\left(I\right)}}<2\mathit\varGamma\) for copolymers with blocks of equal length. In terms of directly measurable quantities, Eq. (12) is \({\varphi }\mathrm{_{AB}^{\left(I\right)}}<\frac{NaS}{{{V}N}_{i}}\). In the papers mentioned, a higher content limit based on a gyration radius \({\widetilde{\varphi }}\mathrm{_{AB}^{\left(I\right)}}<6\mathit\varGamma\) was used.

The copolymer blocks are stretched, and the brush is thicker for a larger copolymer concentration at the interface. Λi can be determined by the minimization of gi at a certain Ψ for the Leibler theory. Unfortunately, this procedure does not provide Λi as an explicit function of Ψ. Therefore, approximations for the dry brush (reliable for copolymer blocks shorter than homopolymers) and for the wet brush (reliable for copolymer blocks longer than homopolymers) in Eq. (10) were made in the previous papers [1, 6, 14, 20]. The use of approximations for the dry and wet brush models sometimes did not provide a smooth transition of their results to the results of calculations for small concentration of a copolymer at the interface [6, 20]. Therefore, we inverted the common procedure of calculation in our recent paper [21]. For each copolymer content in the interfacial layer (which is the dependent quantity), the corresponding interfacial layer thickness was calculated, and from both, the related total copolymer content in the system was expressed. This procedure enables us to avoid approximations in Eq. (10) (expression for Ff). The equation expressing the equality of the copolymer chemical potentials at the interface and in the bulk A and B phases can be formulated as [21]

$${\varphi }_\text{AB}={\varphi }_\text{AB}^\text{(I)}+[{\varphi }_\text{A}\text{exp}\{-\chi {N}_\text{B}\}+{\varphi }_\text{B}\text{exp}\{-\chi {N}_\text{A}\}]\text{exp}\left\{\frac{{\mu }_\text{I}}{kT}\right\}$$
(13)

Using the original Leibler’s expression for the Gibbs energy of the interfacial film, the following equation was derived for chemical potential, µI,L, of a copolymer in the interfacial layer for a low content of the copolymer (unstretched blocks) [21]

$$\begin{aligned}\frac{{\mu }_\mathrm{I,L}}{kT}=&\ \mathrm{ln}\left( {N}_\mathrm{A}\mathit\varPsi \right)+\mathrm{ln}\left( {N}_\mathrm{B}\mathit\varPsi \right)-\frac{{N}_\mathrm{A}}{{P}_\mathrm{A}}\left[1+\mathrm{ln}\left(1-{N}_\mathrm{A}^\frac{1}{2}\mathit\varPsi \right)\right]\\&-\frac{{N}_\mathrm{B}}{{P}_\mathrm{B}}\left[1+\mathrm{ln}\left(1-{N}_\mathrm{B}^\frac{1}{2}\mathit\varPsi \right)\right]+5\end{aligned}$$
(14)

The following equation was derived for µI,L in the case of a high content of a copolymer at the interface (stretched blocks) [21]

$$\begin{aligned}\frac{{\mu }_\mathrm{I,L}}{kT}=&\ \mathrm{ln}\left( {N}_\mathrm{A}\mathit\varPsi \right)+\mathrm{ln}\left({N}_\mathrm{B}\mathit\varPsi \right)+\left[\frac{{N}_\mathrm{A}^{2}}{{P}_\mathrm{A}{\mathit\varLambda }_\mathrm{A}}+\frac{{N}_\mathrm{B}^{2}}{{P}_\mathrm{B}{\mathit\varLambda }_\mathrm{B}}+3\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\right]\mathit\varPsi\\& +2-\left(\frac{{N}_\mathrm{A}}{{P}_\mathrm{A}}+\frac{{N}_\mathrm{B}}{{P}_\mathrm{B}}\right)+\frac{3}{2}\left(\frac{{\mathit\varLambda }_\mathrm{A}^{2}}{{N}_\mathrm{A}}+\frac{{\mathit\varLambda }_\mathrm{B}^{2}}{{N}_\mathrm{B}}\right)\end{aligned}$$
(15)

where relation between Ψ and Λi is given by the equation

$$\frac{1}{\mathit\varPsi {P}_{i}}\mathrm{ln}\left(1-\frac{{N}_{i}\mathit\varPsi }{{\mathit\varLambda }_{i}}\right)+\frac{{N}_{i}}{{P}_{i}{\mathit\varLambda }_{i}}+3\frac{{\mathit\varLambda }_{i}}{{N}_{i}}=0$$
(16)

The following equations follows from Leibler’s model for correction of the interfacial tension for a low content of a copolymer at the interface [21]

$$\begin{aligned}-\frac{{\gamma }_{\mathrm{L}}-{\gamma }_{0}}{{\gamma }_{0}}\sqrt{\frac{\mathit\chi }{6}}=&\ \mathit\varPsi \left[2-\left(\frac{{N}_\mathrm{A}}{{P}_\mathrm{A}}+\frac{{N}_\mathrm{B}}{{P}_\mathrm{B}}\right)\right]\\&-\left[\frac{{N}_\mathrm{A}^\frac{1}{2}}{{P}_\mathrm{A}}\mathrm{ln}\left(1-{N}_\mathrm{A}^\frac{1}{2}\mathit\varPsi \right)+\frac{{N}_\mathrm{B}^\frac{1}{2}}{{P}_\mathrm{B}}\mathrm{ln}\left(1-{N}_\mathrm{B}^\frac{1}{2}\mathit\varPsi \right)\right]\end{aligned}$$
(17)

For the same model, the following equation was derived for the interfacial tension correction when a high content of a copolymer at the interface was considered [21]

$$-\frac{{\gamma }_{\mathrm{L}}-{\gamma }_{0}}{{\gamma }_{0}}\sqrt{\frac{\mathit\chi }{6}}=\mathit\varPsi \left[2+3\left(\frac{{\mathit\varLambda }_\mathrm{A}^{2}}{{N}_\mathrm{A}}+\frac{{\Lambda }_\mathrm{B}^{2}}{{N}_\mathrm{B}}\right)\right]$$
(18)

where relation between Ψ and Λi, given by Eq. (16) is to be applied.

When ΔγR, given by Eq. (4), is considered in Eq. (3) for Ff, the following equation was derived for chemical potential of a copolymer in the interfacial layer, µI,R, in the case of a low content of a copolymer at the interface [21]

$$\frac{{\mu }_\mathrm{I,R}}{kT}=\frac{{\mu }_\mathrm{I,L}}{kT}+\mathrm{ln}\frac{{\left(24\chi \right)}^\frac{1}{2}\left({N}_\mathrm{A}^\frac{1}{2}+{N}_\mathrm{B}^\frac{1}{2}\right)}{\pi }$$
(19)

We compared the effect of calculation of the relation between Ψ and Λi by minimization of gi and by minimization of Ff, given by Eq. (3), on the chemical potential and correction of the interfacial tension using Eq. (4) for ΔγR. Only negligible differences between results of these two approaches were found. Therefore, for simplicity, Eq. (16) following from the minimization of gi is used for the relation between Ψ and Λi also when non-zero Δγ is considered. Using this assumption, the following equation for µI,R was derived for a high content of a copolymer at the interface [21]

$$\begin{aligned}\frac{{\mu }_\mathrm{I,R}}{kT}=&\ \frac{{\mu }_\mathrm{I,L}}{kT}+\mathrm{ln}\frac{{\left(24\chi \right)}^\frac{1}{2}\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)}{\pi }-1+\frac{2\mathit\varPsi }{\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)}\\&\left(\frac{{N}_\mathrm{A}^{2}}{\frac{{N}_\mathrm{A}^{2}}{{\mathit\varLambda }_\mathrm{A}}+3\frac{{P}_\mathrm{A}}{{N}_\mathrm{A}}-3{P}_\mathrm{A}{\mathit\varLambda }_\mathrm{A}\mathit\varPsi }+\frac{{N}_\mathrm{B}^{2}}{\frac{{N}_\mathrm{B}^{2}}{{\mathit\varLambda }_\mathrm{B}}+3\frac{{P}_\mathrm{B}}{{N}_\mathrm{B}}-3{P}_\mathrm{B}{\mathit\varLambda }_{B}\mathit\varPsi }\right)\end{aligned}$$
(20)

where Eq. (16) determines the relation between Ψ and Λi. For a low content of a copolymer at the interface, Eq. (17) for Leibler’s model is valid also for correction of the interfacial tension in the Retsos modification of Leibler’s theory.

For a high content of a copolymer at the interface, the following equation was derived for the decrease in the interfacial tension considering ΔγR in Eq. (3) for Ff [21]

$$\begin{aligned}-\frac{{\gamma }_\mathrm{R}-{\gamma }_{0}}{{\gamma }_{0}}\sqrt{\frac{\mathit\chi }{6}}=&\ \mathit\varPsi \left[1+3\left(\frac{{\mathit\varLambda }_\mathrm{A}^{2}}{{N}_\mathrm{A}}+\frac{{\mathit\varLambda }_\mathrm{B}^{2}}{{N}_\mathrm{B}}\right)+\frac{2\mathit\varPsi }{{\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}}\right.\left.\left(\frac{{N}_\mathrm{A}^{2}}{\frac{{N}_\mathrm{A}^{2}}{{\mathit\varLambda }_\mathrm{A}}\mathit\varPsi +3\frac{{P}_\mathrm{A}}{{N}_\mathrm{A}}{\mathit\varLambda }_\mathrm{A}^{2}-3{P}_\mathrm{A}{\mathit\varLambda }_\mathrm{A}\mathit\varPsi }+\frac{{N}_\mathrm{B}^{2}}{\frac{{N}_\mathrm{B}^{2}}{{\mathit\varLambda }_\mathrm{B}}\mathit\varPsi +3\frac{{P}_\mathrm{B}}{{N}_\mathrm{B}}{\mathit\varLambda }_\mathrm{B}^{2}-3{P}_\mathrm{B}{\mathit\varLambda }_\mathrm{B}\mathit\varPsi }\right)\right]\end{aligned}$$
(21)

The relation between Ψ and Λi is given by Eq. (16).

Expression of Noolandi’s Δγ through the Leibler model parameters

Noolandi stated [15] that main contribution to Δγ was given by the equation derived by Noolandi and Hong [16]

$$\Delta \gamma \simeq \int \left\{\frac{{\varphi }_{\mathrm{C}}\left(x\right)}{N}\mathrm{ln}\frac{{\varphi }_{\mathrm{C}}\left(x\right)}{{\varphi }_\mathrm{C}}-\frac{{\varphi }_\mathrm{C}\left(x\right)-{\varphi }_\mathrm{C}}{N}-\frac{1}{2}\chi {\varphi }_\mathrm{P}\left[{\varphi }_\mathrm{C}\left(x\right)-{\varphi }_\mathrm{C}\right]\right\}\mathrm dx$$
(22)

Equation (3–8) of ref. [16] is reproduced here because the brackets are incorrectly placed in Eq. (3) of ref. [15]. In ref. [16], φC(x) is the position dependent volume concentration of a copolymer in the interfacial region, φC is the volume concentration of the copolymer far from the interface, φP is the volume concentration of homopolymers far from the interface, and x is the coordinate perpendicular to the interface. Equation (22) was derived under the assumptions:

$$P_\mathrm{A}=P_\mathrm{B}\rightarrow\infty,\;N_\mathrm{A}=N_\mathrm{B},\;\varphi_\mathrm{A}=\varphi_\mathrm{B},\;\varphi_\mathrm{AB}^\mathrm{(A)}+\varphi_\mathrm{AB}^\mathrm{(B)}\rightarrow\varphi_\mathrm{AB}$$

When different volume fractions of homopolymers A and B, copolymers with different block lengths and \({\varphi }\mathrm{_{AB}^{\left(I\right)}}\) non-negligible with respect to φAB are assumed, Eq. (22) can be generalized as

$$\begin{aligned}\Delta \gamma =&\ {\int }_{-{L}_\mathrm{A}}^{0}\left\{\frac{{\varphi }\mathrm{_{C}^{\left(A\right)}}\left(x\right)}{N}\mathrm{ln}\frac{{\varphi }\mathrm{_{C}^{\left(A\right)}}\left(x\right)}{{\varphi }\mathrm{_{C}^{\left(A\right)}}}-\frac{{\varphi }\mathrm{_{C}^{\left(A\right)}}\left(x\right)-{\varphi }\mathrm{_{C}^{\left(A\right)}}}{N}-\frac{1}{2}\mathit\chi {\varphi }_\mathrm{P}^\mathrm{\left(A\right)}\left[{\varphi }\mathrm{_{C}^{\left(A\right)}}\left(x\right)-{\varphi}\mathrm{_{C}^{\left(A\right)}}\right]\right\}\mathrm dx \\&+{\int }_{0}^{{L}_{\mathrm{B}}}\left\{\frac{{\varphi }\mathrm {_{C}^{\left(B\right)}}\left(x\right)}{N}\mathrm{ln}\frac{{\varphi }\mathrm{_{C}^{\left(B\right)}}\left(x\right)}{{\varphi }\mathrm{_{C}^{\left(B\right)}}}-\frac{{\varphi }\mathrm{_{C}^{\left(B\right)}}\left(x\right)-{\varphi }\mathrm{_{C}^{\left(B\right)}}}{N}-\frac{1}{2}\mathit\chi {\varphi }\mathrm{_{P}^{\left(B\right)}}\left[{\varphi }\mathrm{_{C}^{\left(B\right)}}\left(x\right)-{\varphi }\mathrm{_{C}^{\left(B\right)}}\right]\right\}\mathrm dx\end{aligned}$$
(23)

where superscripts A and B indicate quantities on the side of A- or B-rich phase from the interface.

Volume concentrations of a copolymer in A and B sides of the interfacial layer can be expressed through quantities used in our preceding papers [6, 20, 21] as

$${\varphi }\mathrm{_{C}^{\left(A\right)}}\left(x\right)=\frac{{Q}\mathrm{_{AB}^{\left(I\right)}}{f}_\mathrm{A}N{a}^{3}}{{L}_\mathrm{A}S}=\frac{{f}_\mathrm{A}{\varphi }\mathrm{_{AB}^{\left(I\right)}}}{{L}_\mathrm{A}{S}_{V}}$$
(24a)
$${\varphi }\mathrm{_{C}^{\left(B\right)}}\left(x\right)=\frac{{Q}\mathrm{_{AB}^{\left(I\right)}}{f}_\mathrm{B}N{a}^{3}}{{L}_\mathrm{B}S}=\frac{{f}_\mathrm{B}{\varphi }\mathrm{_{AB}^{\left(I\right)}}}{{L}_\mathrm{B}{S}_{V}}$$
(24b)

where fi = Ni/N is the ratio of the length of i-block to the length of the whole copolymer. The following equations are valid for concentrations of the copolymer in bulk A-rich and B-rich phases

$${\varphi }\mathrm{_{C}^{\left(A\right)}}=\frac{{Q}\mathrm{_{AB}^{\left(A\right)}}N{a}^{3}}{{V}_\mathrm{A}}=\frac{{\varphi }\mathrm{_{AB}^{\left(A\right)}}}{\left(\frac{{V}_\mathrm{A}}{V}\right)}$$
(25a)
$${\varphi }\mathrm{_{C}^{\left(B\right)}}=\frac{{Q}\mathrm{_{AB}^{\left(B\right)}}N{a}^{3}}{{V}_\mathrm{B}}=\frac{{\varphi }\mathrm{_{AB}^{\left(B\right)}}}{\left(\frac{{V}_\mathrm{B}}{V}\right)}$$
(25b)

Using the relation between \({\varphi }\mathrm{_{AB}^{\left(A\right)}}\) and \({\varphi }\mathrm{_{AB}^{\left(B\right)}}\), following from equality of chemical potentials of a copolymer in A and B phases [6, 14, 20]

$${\varphi }\mathrm{_{AB}^{\left(A\right)}}={\varphi }\mathrm{_{AB}^{\left(B\right)}}\frac{{\varphi }_\mathrm{A}}{{\varphi }_\mathrm{B}} {e}^{\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}$$
(26)

\({\varphi }\mathrm{_{AB}^{\left(A\right)}}\) and \({\varphi }\mathrm{_{AB}^{\left(B\right)}}\) can be expressed as

$${\varphi }\mathrm{_{AB}^{\left(A\right)}}=\frac{{\varphi }_\mathrm{AB}-{\varphi }\mathrm{_{AB}^{\left(I\right)}}}{1+{\widetilde{\varphi }}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}}$$
(27a)
$${\varphi }\mathrm{_{AB}^{\left(B\right)}}=\frac{\left({\varphi }_\mathrm{AB}-{\varphi }\mathrm{_{AB}^{\left(I\right)}}\right){\widetilde{\varphi }}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}}{1+{\widetilde{\varphi }}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}}$$
(27b)

where \({\widetilde{\varphi }}_\mathrm{B}\) = φB/φA.

Generally, A-rich (B-rich) phase contains A (B) homopolymer and dissolved copolymer. On the other hand, a part of A (B) homopolymer is dissolved in A (B) side of the interfacial layer. For polymer blends where the amount of added copolymer is small with respect to the amounts of its components and lengths of the copolymer blocks are not too different, the following approximation can be used for the ratio of volumes of A-rich and B-rich phases

$$\frac{{V}_\mathrm{B}}{{V}_\mathrm{A}}=\frac{{\varphi }_\mathrm{B}}{{\varphi }_\mathrm{A}}={\widetilde{\varphi }}_\mathrm{B}$$
(28)

Using Eq. (28), the following equations can be derived for VA and VB

$$\frac{{V}_\mathrm{A}}{V}=\frac{1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}}{1+{\widetilde{\varphi }}_\mathrm{B}}$$
(29a)
$$\frac{{V}_\mathrm{B}}{V}=\frac{\left[1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}\right]{\widetilde{\varphi }}_\mathrm{B}}{1+{\widetilde{\varphi }}_\mathrm{B}}$$
(29b)

Substitution of \({\varphi }\mathrm{_{AB}^{\left(A\right)}}\) from Eq. (27a) and \(\frac{{V}_\mathrm{A}}{V}\) from Eq. (29a) into Eq. (25a) and \({\varphi }\mathrm{_{AB}^{\left(B\right)}}\) from Eq. (27b) and \(\frac{{V}_\mathrm{B}}{V}\) from Eq. (29b) into Eq. (25b) leads to

$${\varphi }\mathrm{_{C}^{\left(A\right)}}=\frac{\left({\varphi }_\mathrm{AB}-{\varphi }\mathrm{_{AB}^{\left(I\right)}}\right)\left(1+{\widetilde{\varphi }}_\mathrm{B}\right)}{\left(1+{\widetilde{\varphi }}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)\left[1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}\right]}$$
(30a)
$${\varphi }\mathrm{_{C}^{\left(B\right)}}=\frac{\left({\varphi }_\mathrm{AB}-{\varphi }_\mathrm{AB}^\mathrm{\left(\mathrm{I}\right)}\right)\left(1+{\widetilde{\varphi }}_\mathrm{B}\right){e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}}{\left(1+{\widetilde{\varphi }}_\mathrm{B}{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)\left[1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}\right]}$$
(30b)

When concentrations of a copolymer dissolved in the bulk phases is small, \({\varphi }\mathrm{_{P}^{\left(A\right)}}\) and \({\varphi }\mathrm{_{P}^{\left(B\right)}}\) can be approximated as

$${\varphi }_\mathrm{P}^\mathrm{\left(A\right)}\cong {\varphi }_\mathrm{P}^\mathrm{\left(B\right)}\cong 1$$
(31)

Substitution of \({\varphi }\mathrm{_{C}^{\left(A\right)}}\left(x\right)\) from Eq. (24a), \({\varphi }\mathrm{_{C}^{\left(B\right)}}\left(x\right)\) from Eq. (24b), \({\varphi }\mathrm{_{C}^{\left(A\right)}}\) from (30a), \({\varphi }\mathrm{_{C}^{\left(B\right)}}\) from (30b), and \({\varphi }\mathrm{_{P}^{\left(A\right)}}\) and \({\varphi }\mathrm{_{P}^{\left(B\right)}}\) from Eq. (31) into Eq. (23) leads to the following equation

$$\begin{aligned}\Delta \gamma =&\ \frac{{f}_\mathrm{A}{\varphi }\mathrm{_{AB}^{\left(I\right)}}}{N{S}_{V}}\mathrm{ln}\frac{C{\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}\left[1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}\right]}{{L}_{\mathrm{A}}{S}_{V}\left({\varphi }_\mathrm{AB}-{\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}\right)}\\&+\frac{{f}_{\mathrm{B}}{\varphi }_{\mathrm{AB}}^\mathrm{\left(I\right)}}{N{S}_{V}}\mathrm{ln}\frac{D{\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}\left[1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}\right]}{{L}_{\mathrm{B}}{S}_{V}\left({\varphi }_\mathrm{AB}-{\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}\right)}-\frac{2+\chi N}{2N}\\&\left\{\frac{{\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}}{{S}_{V}}-\frac{E\left({\varphi }_\mathrm{AB}-{\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}\right)\left({L}_\mathrm{A}+{L}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)}{\left[1-\left({L}_\mathrm{A}+{L}_\mathrm{B}\right){S}_{V}\right]}\right\}\end{aligned}$$
(32)

where

$$C=\frac{{f}_\mathrm{A}\left(1+{\widetilde{\varphi }}_\mathrm{B} {e}^{-\mathit\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)}{\left(1+{\widetilde{\varphi }}_\mathrm{B}\right)}$$
(33)
$$D=\frac{{f}_\mathrm{B}\left(1+{\widetilde{\varphi }}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)}{\left(1+{\widetilde{\varphi }}_\mathrm{B}\right){e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}}$$
(34)
$$E=\frac{1+{\widetilde{\varphi }}_\mathrm{B}}{1+{\widetilde{\varphi }}_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}}$$
(35)

Δγ in Eq. (22) of refs. [15, 16] is considered in kT units for unit number of segments in a unit volume. Therefore, the change in the interfacial tension with dimensions consistent with interfacial tension considered for substitution into Eq. (3) for Ff and ΔγN has to be expressed as

$$\Delta {\gamma }_\mathrm{N}=\frac{kT}{{a}^{3}}\Delta \gamma$$
(36)

It follows from Eqs. (3) and (5) that a derivative of the product of ΔγN with S with respect to \({Q }\mathrm{_{AB}^{\left(I\right)}}\) has to be calculated for determination of chemical potential, μI,N, for Noolandi’s and Hong’s model. Substitution Δγ from Eq. (32) to Eq. (36) and differentiation of product ΔγNS leads to the following equation

$$\begin{aligned}\frac{1}{kT}{\left(\frac{\partial \left[\Delta {\gamma }_\mathrm{N}S\right]}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}\right)}_{S}=&\ {f}_\mathrm{A}\mathrm{ln}\frac{C{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}{\mathit\varGamma {\varphi }_\mathrm{A}{\mathit\varLambda }_\mathrm{A}\left({Q}_\mathrm{AB}-{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\right)}+{f}_\mathrm{B}\mathrm{ln}\frac{D{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}{\mathit\varGamma {\varphi }_\mathrm{A}{\mathit\varLambda }_\mathrm{B}\left({Q}_\mathrm{AB}-{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\right)}\\&+1-\frac{{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\mathit\varGamma {\varphi }_\mathrm{A}\left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}\right)}{1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}}+\frac{{Q}_\mathrm{AB}^\mathrm{\left(I\right)}}{{Q}_\mathrm{AB}-{Q}_\mathrm{AB}^\mathrm{\left(I\right)}}-{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\left({f}_\mathrm{A}\frac{\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}}{{\mathit\varLambda }_\mathrm{A}}+{f}_\mathrm{B}\frac{\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}}{{\mathit\varLambda }_\mathrm{B}}\right)\\&-\frac{2+\chi N}{2}\left[1+\frac{E\left[{\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right]\mathit\varGamma {\varphi }_\mathrm{A}}{1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}}\right]\\&+\frac{2+\chi N}{2}\frac{E\mathit\varGamma {\varphi }_\mathrm{A}\left({Q}_\mathrm{AB}-{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\right)\left[\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}+\mathit\varGamma {\varphi }_\mathrm{A}\left({\mathit\varLambda }_\mathrm{A}\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}-{\mathit\varLambda }_\mathrm{B}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}\right)\left(1-{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)\right]}{{\left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}^{2}}\end{aligned}$$
(37)

where Eqs. (7) and (9) are used for substitution of SV and Li.

Using definition Ψ by Eq. (8) and relations between volume fractions and relating number of molecules lead to the equations

$${Q}_\mathrm{AB}^\mathrm{\left(I\right)}=\frac{V{\varphi }_\mathrm{A}\mathit\varGamma }{{a}^{3}}\mathit\varPsi$$
(38)
$$\frac{\partial {\mathit\varLambda }_{i}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}=\frac{{a}^{3}}{V{\varphi }_\mathrm{A}\mathit\varGamma }\frac{\partial {\mathit\varLambda }_{i}}{\partial \mathit\varPsi }$$
(39)
$${Q}_\mathrm{AB}=\frac{V{\varphi }_\mathrm{AB}}{N{a}^{3}}$$
(40)

Substitution of \({Q}_\mathrm{AB}^\mathrm{\left(I\right)}\) from Eq. (38), \(\frac{\partial {\mathit\varLambda }_{i}}{\partial {Q}_\mathrm{AB}^\mathrm{\left(I\right)}}\), from Eq. (39), and QAB from Eq. (40) to Eq. (37) and resulting equation into Eq. (3) provides the following equation for chemical potential of copolymer at the interface for the Noolandi-Hong model

$$\begin{aligned}\frac{{\mu }_\mathrm{I,N}}{kT}=&\ \frac{{\mu }_\mathrm{I,L}}{kT}+{f}_\mathrm{A}\mathrm{ln}\frac{CN\mathit\varPsi \left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}{{\mathit\varLambda }_\mathrm{A}\left({\varphi }_\mathrm{AB}-\mathit\varGamma {\varphi }_\mathrm{A}N\mathit\varPsi \right)}+{f}_\mathrm{B}\mathrm{ln}\frac{DN\mathit\varPsi \left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}{{\mathit\varLambda }_\mathrm{B}\left({\varphi }_\mathrm{AB}-\mathit\varGamma {\varphi }_\mathrm{A}N\mathit\varPsi \right)}\\&+1+\frac{\mathit\varGamma {\varphi }_\mathrm{A}N\mathit\varPsi }{{\varphi }_\mathrm{AB}-\mathit\varGamma {\varphi }_\mathrm{A}N\mathit\varPsi }-\frac{\mathit\varGamma {\varphi }_\mathrm{A}\mathit\varPsi \left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }\right)}{1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}}-\mathit\varPsi \left(\frac{{f}_\mathrm{A}\left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }\right)}{{\mathit\varLambda }_\mathrm{A}}+\frac{{f}_{\mathrm{B}}\left(\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }\right)}{{\mathit\varLambda }_\mathrm{B}}\right)\\&-\frac{2+\chi N}{2}\left\{1+\frac{E\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)\mathit\varGamma {\varphi }_\mathrm{A}}{1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}}\right\}\\&+\frac{2+\chi N}{2}\frac{E\left(\frac{{\varphi }_\mathrm{AB}}{N}-\mathit\varGamma {\varphi }_\mathrm{A}\mathit\varPsi \right)\left[\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}+ \mathit\varGamma {\varphi }_\mathrm{A}\left({\mathit\varLambda }_\mathrm{A}\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }-{\mathit\varLambda }_\mathrm{B}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }\right)\left(1-{e}^{-\chi \left({N}_{\mathrm{A}}-{N}_\mathrm{B}\right)}\right)\right]}{{\left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}^{2}}\end{aligned}$$
(41)

Derivative of ΔγNS with respect to S has to be calculated for determination of the interfacial tension.

$$\begin{aligned}\frac{1}{kT}{\left(\frac{\partial \left[\Delta {\gamma }_\mathrm{N}S\right]}{\partial S}\right)}_{{Q}_\mathrm{AB}^\mathrm{\left(I\right)}}=&\ -{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\left\{\frac{a}{V}\frac{\left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial S}+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial S}\right)S+{\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}}{1-a\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right){S}_{V}}+\frac{1}{S}+\frac{{f}_\mathrm{A}}{{\mathit\varLambda }_\mathrm{A}}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial S}+\frac{{f}_\mathrm{B}}{{\mathit\varLambda }_\mathrm{B}}\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial S}\right\}+\frac{2+\chi N}{2}E\frac{a}{V}\left({Q}_\mathrm{AB}-{Q}_\mathrm{AB}^\mathrm{\left(I\right)}\right) \\&\frac{\left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial S}+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial S} {e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)S+{\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}+aV{{S}_{V}}^{2}\left(1-{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)\left({\mathit\varLambda }_\mathrm{A}\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial S}-{\mathit\varLambda }_{\mathrm{B}}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial S}\right)}{{\left[1-a\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right){S}_{V}\right]}^{2}}\end{aligned}$$
(42)

Derivative of Λi with respect to S can be expressed as [21]

$$\frac{\partial {\mathit\varLambda }_{i}}{\partial S}=-\frac{a\mathit\varPsi }{V\mathit\varGamma {\varphi }_\mathrm{A}}\frac{\partial {\mathit\varLambda }_{i}}{\partial \mathit\varPsi }$$
(43)

After substitution of Γ from Eq. (7), Λi from Eq. (9), \({Q}_\mathrm{AB}^\mathrm{\left(I\right)}\) from Eq. (38), QAB from Eq. (40), and \(\frac{\partial {\mathit\varLambda }_{i}}{\partial S}\) from Eq. (43) into Eq. (42) and gradual substitution of this result into Eqs. (3) and (6), the following equation for interfacial tension of the Noolandi and Hong model is derived

$$\begin{aligned}{\gamma }_\mathrm{N}=&\ {\gamma }_\mathrm{L}+\frac{kT}{{a}^{2}}\left\{-\mathit\varGamma {\varphi }_\mathrm{A}\mathit\varPsi \frac{{\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}-\mathit\varPsi \left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }\right)}{1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_{\mathrm{A}}}-\mathit\varPsi +{\mathit\varPsi }^{2}\left(\frac{{f}_\mathrm{A}}{{\mathit\varLambda }_\mathrm{A}}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }+\frac{{f}_\mathrm{B}}{{\mathit\varLambda }_\mathrm{B}}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }\right)\right\}+\frac{kT}{{a}^{2}}E\frac{2+\chi N}{2}\\&\left\{\left(\frac{{\varphi }_\mathrm{AB}}{N}-\mathit\varGamma {\varphi }_\mathrm{A}\mathit\varPsi \right)\frac{{\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}-\mathit\varPsi \left(\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }+\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }\right)+\mathit\varGamma {\varphi }_\mathrm{A}\mathit\varPsi \left(1-{e}^{-\chi \left({N}_\mathrm{A}-{N}_\mathrm{B}\right)}\right)\left({\mathit\varLambda }_\mathrm{B}\frac{\partial {\mathit\varLambda }_\mathrm{A}}{\partial \mathit\varPsi }-{\mathit\varLambda }_{\mathrm{A}}\frac{\partial {\mathit\varLambda }_\mathrm{B}}{\partial \mathit\varPsi }\right)}{{\left[1-\left({\mathit\varLambda }_\mathrm{A}+{\mathit\varLambda }_\mathrm{B}\right)\mathit\varGamma {\varphi }_\mathrm{A}\right]}^{2}}\right\}\end{aligned}$$
(44)

For a low copolymer concentration at the interface (copolymer blocks are not stretched) Λi is given by Eq. (11) and its derivative with respect to Ψ is zero. For a large copolymer concentration at the interface (copolymer blocks are stretched), Λi and its derivative is to be determined using Eq. (16) by the procedure described in our previous paper [21].

Calculation procedure

The calculation procedure from our previous paper [21] was used. However, this procedure was based on calculation of total copolymer content φAB from the resulting copolymer content at the interface. Since Eq. (41) contains φAB, it could not be obtained explicitly from Eq. (7) of ref. [21], but the equation was solved numerically (supposing φAB dependent last term of its right-hand side) using bisection method combined with regula falsi. Both Λi were obtained as in paper [21] in Leibler’s model, since its exact solution considering the additional term defined in Eq. (41) would significantly complicate the procedure. The comparison in [21] shows that using of Λi obtained for the Leibler model does not affect significantly the results in other models. As explained below after Fig. 1, we have chosen Eq. (12) as the rule for application of low copolymer content formulae.

Fig. 1
figure 1

The calculated dependences of copolymer contents in the interfacial layer on total copolymer content for low (left column) and higher (right column) copolymer content in the interfacial layer versions of three models mentioned in the text. Copolymer blocks length NA = NB of 200 (a), 240 (b), 300 (c), and 400 (d). Homopolymer chain lengths PA = PB = 250. The Flory–Huggins interaction parameter was χAB = 0.04. Interfacial area to volume parameter Γ = 0.00525. Volume fraction of the dispersed phase: φA = 0.3; segment length a = 0.7 nm. More details in the text

Full size image

The regime of low copolymer contents is suggested for copolymer amount in the interfacial layer \({\varphi }_\mathrm{AB}^\mathrm{\left(I\right)}<\frac{NaS}{{VN}_{i}}\); however, this amount should be first calculated by this model, and only then, the compliance with the rule can be evaluated.

Results

First, Fig. 1 compares the calculated dependences of copolymer contents in the interfacial layer on total copolymer content presented in Fig. 8 of ref. [21] with the dependences following from Noolandi’s modification of the theory derived in this paper. The copolymer content results obtained using formula (14) for lower copolymer contents at the interface are labeled as “Leibler” and represented by circles in the left column, those using formula (15) for higher copolymer content labeled also as Leibler and represented by circles in the right column. Those obtained by addition of correction by Eqs. (19) and (20) to those of Eqs. (14) and (15), respectively, are labeled as Noolandi-Retsos and represented by diamonds in the left and right columns, respectively. Those obtained by addition of the correction according to Eq. (41) to those of Eqs. (14) and (15), respectively, are labeled Noolandi-Hong and represented by squares in the left and right columns, respectively.

Figure 1 shows that the Noolandi and Hong correction by Eq. (41) provides higher copolymer content at the interface than models considered in our previous papers [21]. Figure 2 shows the calculated decrease in the interfacial tension due to copolymer addition for the same system. The limit for positive logarithm argument in Eq. (17) marked with the dashed gray horizontal line in the upper part of the graphs in Fig. 1 is sufficiently higher than the limits in question. The limit derived from the average gyration radius, marked by the middle dash-dotted horizontal line, and the limit given by the end-to-end distance by Eq. (12), marked by the lowest black dash-dotted horizontal line. The absolute difference in results provided by Eq. (14) for lower copolymer content at the interface from that obtained by Eq. (15) for higher content increases with copolymer contents. Together with a consideration of full surface coverage, we decided to use the limit given by inequality (12) for the subsequent comparisons.

Fig. 2
figure 2

The calculated dependences of decrease in the interfacial tension on total copolymer content. Parameters as in Fig. 1

Full size image

Figure 2 demonstrates that the Noolandi-Hong modification predicts faster decrease in the interfacial tension with the amount of added copolymer than the original Leibler theory and its modification proposed by Retsos et al. [17] and Anastasiadis [12] (Noolandi-Retsos). The Leibler model simplifies in comparison with the real structure—it treats a surface layer boundary as sharp, using the Flory–Huggins model. The calculation based on the Noolandi-Hong modification is expected to be more precise than the other two. However, usage of interfacial thickness calculated according to the Leibler model for reasons stated in the calculation procedure section constitutes an additional source of possible mistakes. The choice between the models could be verified using a large amount of experimental data that we did not have at our disposal. However, the Noolandi-Hong modification may represent the upper limit of compatibilization efficiency.

We have calculated the relative decrease in interfacial tension as a function of copolymer blocks length for the copolymer volume fraction system. The calculation has been made for the systems and parameters presented in Fig. 11 of ref. [6] and Fig. 3 of ref. [4]. The comparison of results obtained by our universal method as described in our paper [21] is presented in Figs. 3 and 4.

Fig. 3
figure 3

Dependence of the reduced copolymer contents at the interface \({\widetilde{\varphi }}_\mathrm{AB}^\mathrm{\left(I\right)}\) on the copolymer blocks length NA = NB in the range from 60 to 1200 for reduced copolymer volume fraction φ̃AB = 0.05 and PA = PB values of 40 (upper graph), 120 (middle graph), and 400 (lower graph). χAB = 0.04, Γ = 0.00525, φA = 0.3, a = 0.7 nm. Formulae (14) and (19) for lower copolymer contents at the interface (thin lines) are used for \({\widetilde{\varphi }}_{\mathrm{AB}}^{\left(\mathrm{I}\right)}<0.0105\), formulae (15) and (20) above this limit (thick lines)

Full size image
Fig. 4
figure 4

Dependence of the relative decrease in the interfacial tension γ on copolymer blocks length NA = NB for the same parameters as in Fig. 3. The regions of validity can be seen from the Fig. 3

Full size image

If we use Eq. (41), the formula for higher copolymer content appears appropriate for nearly the whole Ni range. There is an overlap of both models for Ni approximately between 100 and 200. Equations (14) and (19) for lower copolymer content provide \({\widetilde{\varphi }}_{\mathrm{AB}}^{\left(\mathrm{I}\right)}\) below the upper limit 0.0105 of its validity; Eqs. (15) and (20) above provide the same value chosen as the lower limit of their validity.

The discontinuity is a weak point of simplified models in their form presented in this article. To choose which of the models is to be used, one should evaluate both of them and compare the calculated copolymer content in the interfacial layer Ψ with its limiting value given by Eq. (12); note that the condition is also expressed using other variables in the text below the equation and that the condition was chosen a bit arbitrarily from more possibilities. In some cases, it can also happen that the low copolymer content formula provides Ψ below 1/Ni and the formula for high copolymer content above 1/Ni; this means each equation is within its range of validity (we will call it an overlap in the further text). In other cases, an opposite inconsistency may happen when each equation provides Ψ in the range where the other models should be applied (there is a gap between the validity ranges). In these cases, we are not able to give a general recommendation on which of the equations to use. Well-known empirical rules come into question, for example, a choice of the regime providing Ψ nearer to 1/Ni in the gap case or a linear (e.g.) combination of results of both formulae sets in both cases.

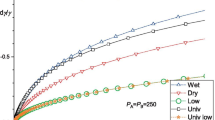
Figure 4 presenting the dependence of the calculated relative decrease in the interfacial tension on the copolymer blocks length documents a maximum for certain Ni. The maximum dependence of compatibility efficiency on copolymer chain length was discussed in previous papers [6, 20]. If the copolymer is too short, too high portion of it is dissolved in the bulk phases and does not contribute to interfacial tension decrease. If the significant copolymer amount is located at the interface, the same copolymer volume fraction (the figures are for constant copolymer volume fraction, not for constant macromolecule number) is constituted by a lower number of copolymer chains with increasing chain length; therefore, the compatibilization efficiency decreases after reaching a maximum.

Figure 4 shows that the model presented in this article based on papers [15] and [16] provides a much stronger decrease in interfacial tension due to copolymer presence than models in our previous papers for higher copolymer contents at the interface. These models were the Leibler model and its modification proposed by Retsos et al. [17] and Anastasiadis [12] in response to Noolandi’s comment. The latter was denoted as Noolandi in refs. [4, 6, 20, 21], while it is denoted as the Noolandi-Retsos in this paper. The copolymer length with the most effective compatibilization was shifted to half of that in previous models. The formula for low copolymer content in the interfacial layer provides a decrease in the interfacial tension that does not follow-up with the decrease obtained using formulae for higher content for this model. The discontinuity is caused by the fact that the solution of Eq. (16) is not Λi = Ni1/2 for Ψ considered as limit for unstretched blocks. In addition, Eq. (44) used to express the decrease in both regions depends significantly on \(\frac{\partial {\mathit\varLambda }_{i}}{\partial \mathit\varPsi }\), which is regarded as zero for low copolymer content and markedly non-zero for higher copolymer content.

The dependence of the calculated copolymer content in the interfacial layer on the copolymer length for three different interfacial areas on volume parameters Γ is presented in Fig. 5, and that of the decrease in the interfacial tension in Fig. 6.

Fig. 5
figure 5

Dependence of the copolymer content in the interfacial region on the copolymer blocks length NA = NB for PA = PB = 120 and Γ values of 0.002125 (upper graph), 0.00525 (middle graph), and 0.0105 (lower graph), respectively. Formulae (14) and (19) for lower copolymer contents at the interface are used for \({\widetilde{\varphi }}_\mathrm{AB}^\mathrm{\left(I\right)}\) below the limit given by Eq. (12) for given Γ (0.00425, 0.0105, and 0.021, respectively; thin lines), formulas (15) and (20) above this limit (thick lines). Other parameters are the same as in Fig. 3

Full size image
Fig. 6
figure 6

Dependence of the relative decrease in the interfacial tension γ on the copolymer blocks length NA = NB. Parameters are the same as in Fig. 5

Full size image

In Fig. 5, it can be seen that Eq. (41) derived in this paper provides higher copolymer contents in the interfacial layer with higher values of the interfacial area to volume parameters Γ. For this specific case, a significant part of the Ni range is covered by formulae for higher copolymer contents, in particular, using formulae derived in this article. In comparison with previously used two formulae, its dependence on copolymer blocks number is flatter. The copolymer contents at the interface are obtained markedly higher than those using previous formulae for shorter copolymer; the calculated values are slightly lower for longer copolymer chains.

As presented in Fig. 6, the decrease in the interfacial tension was calculated using Eqs. (41) and (44) derived in this paper are markedly stronger than that using previous models. For lower Γ parameter values, calculated values of decrease in the interfacial tension exceed the original interfacial tension itself, which means that they provide physically unreasonable negative interfacial tension values. For Γ = 0.0105, the maximum of the compatibilization effect is calculated for copolymer blocks length of approximately half of that in other models. Results for Noolandi’s model, considered in this paper and represented by dash-dotted lines in the figure, lead to the qualitatively same result as the model considered in our previous papers [4, 6, 20], i.e. that block copolymer with the block lengths similar to the lengths of compatibilized homopolymers are the most efficient compatibilizers. However, this Noolandi’s model predicts the highest compatibilization efficiency for a block somewhat shorter than the homopolymers. This is in contrast to previous models predicting that copolymer with somewhat longer blocks than the homopolymers are the most efficient compatibilizers.

For reasons mentioned in the previous paragraph, next comparisons of calculated values were made for Γ = 0.0105. Figures 7 and 8 present the same dependences as Figs. 5 and 6 for different dispersed phase content and Figs. 9 and 10 for different Flory–Huggins interaction parameters.

Fig. 7
figure 7

Dependence of the copolymer content in the interfacial region on the copolymer blocks length NA = NB. Γ = 0.0105, φA of 0.1 (upper graph), 0.3 (middle graph), and 0.5 (lower graph). The low \({\widetilde{\varphi }}_\mathrm{AB}^\mathrm{\left(I\right)}\) limit 0.021. Other parameters are the same as in Fig. 5

Full size image
Fig. 8
figure 8

Dependence of the relative decrease in the interfacial tension γ on the copolymer blocks length NA = NB for various volume fractions of the dispersed phase. Parameters are the same as in Fig. 7

Full size image
Fig. 9
figure 9

Dependence of the copolymer content in the interfacial region on the copolymer blocks length NA = NB for the χAB values of 0.01 (upper graph), 0.04 (middle graph), and 0.08 (lower graph). Other parameters are the same as in Fig. 7

Full size image
Fig. 10
figure 10

Dependence of the relative decrease in the interfacial tension γ on the copolymer blocks length NA = NB. Parameters are the same as in Fig. 9

Full size image

An increase in the dispersed phase content leads to the increased calculated copolymer content at the interface for all three models.

The qualitative findings stated with the precedent figures remain. In addition, Fig. 8 shows that the increase in dispersed phase volume leads to an increase in compatibilization efficiency for shorter copolymer chains. It also leads to a shift of copolymer length with maximal compatibilization efficiency to shorter values. This shift is most noticeable for Eq. (41) expressing the copolymer chemical potential, and thus its content at the interface and (44) expressing the interfacial tension represented by dash-dotted lines.

Figure 9 shows that the higher the Flory–Huggins interaction parameter, the higher the copolymer content at the interface for all models.

From Fig. 10, it is apparent that the increasing Flory–Huggins interaction parameter shifts the maximum of compatibilization efficiency to shorter copolymer lengths and slightly increases the compatibilization efficiency. For the formula presented in this paper, the shift seems to be less pronounced than for other models. Value of χAB has only small effect on the maximum reduction of the interfacial tension in the dependence on the length of copolymer blocks. The calculated maximum for χAB = 0.04 is calculated lower than that for the remaining values in the Noolandi and Hong model. Therefore, we have tested how the value of the Flory–Huggins interaction parameter affects the calculated value of the maximum decrease in the interfacial tension and the copolymer blocks length of this maximum. The dependence is presented in Fig. 11.

Fig. 11
figure 11

Dependence of the maximum relative decrease in the interfacial tension γ (right) and the copolymer blocks length NA = NB for which the maximum Nmax is calculated (left) on the Flory–Huggins interaction parameter. The Leibler model overlaps with the Noolandi and Retsos one in the right graph. Parameters are the same as in Fig. 10

Full size image

While the copolymer blocks length of maximal compatibilization efficiency decreases nearly proportionally to the logarithm of χ, the maximal absolute value of decrease in the interfacial tension due to copolymer addition is smallest for χ near to 0.02 for the Leibler and Noolandi-Retsos formulae, and near to 0.03 for the formulae including the additional term by Noolandi and Hong. We have no explanation. However, the non-monotonous dependence on the interaction parameter should be considered.

Conclusions

The correction of the interfacial tension in the Leibler expression for copolymer chemical potential at the interface between immiscible homopolymers [14], proposed by Noolandi [15], has been explicitly expressed for the Leibler model of the interface.

The amount of a copolymer at the interface and a decrease in the interfacial tension calculated by the universal method, proposed in our previous paper [21], using expression derived in this paper have been compared with their values calculated for the original Leibler model and for the modification of this model proposed by Retsos et al. [17] and Anastasiadis [12] with respect to Noolandi’s suggestion [15]. These last two models were used in our previous papers [6, 20, 21].

The model by Noolandi and Hong [15, 16], treated in this paper, predicts larger amount of a copolymer localized at the interface and larger reduction of the interfacial tension than the models used so far. The Noolandi and Hong model predicts the highest compatibilization efficiency for block copolymers having length of blocks comparable with compatibilized homopolymers. However, in contrast to the other models, it predicts maximum compatibilization efficiency for copolymers with blocks somewhat shorter than the homopolymers. This maximum in the dependence on the copolymer blocks length reaches its lowest value for some value of the Flory–Huggins interaction parameter.

To decide between the regimes of low- and high-copolymer contents at the interface, results of both models have to be obtained first and only then the compliance with the rule can be evaluated. Although we feel the Noolandi and Hong model to be best describing the system, the results do not entitle us to recommend preferring one of the three compared models; the estimates using the Noolandi and Hong modification might be taken as an upper limit for compatibilization efficiency.

Our series of papers [4, 6, 20, 21] enables us to avoid approximations used in derivation of the equations for dry and wet brush models. When a low amount of the copolymer is localized at the interface, copolymer blocks do not overlap and form the Gaussian coils. When the interface is densely occupied with copolymer molecules, overlapping blocks are stretched. Equations for \({\widetilde{\varphi }}_\mathrm{AB}^\mathrm{\left(I\right)}\) and its calculated values, which should be compared with criterium for blocks overlapping, differ for these cases. If the differences between the values of \({\widetilde{\varphi }}_\mathrm{AB}^\mathrm{\left(I\right)}\) calculated on the assumptions of low and high density of a copolymer at the interface are substantial, there is some uncertainty in the choice of the proper method. This paper reflects Noolandi’s suggestion to modify interfacial tension [15].