Climate change information over Fenno-Scandinavia produced with a convection-permitting climate model

Abstract

This paper presents results from high-resolution climate change simulations that permit convection and resolve mesoscale orography at 3-km grid spacing over Fenno-Scandinavia using the HARMONIE-Climate (HCLIM) model. Two global climate models (GCMs) have been dynamically down-scaled for the RCP4.5 and RCP8.5 emission scenarios and for both near and far future periods in the 21st century. The warmer and moister climate conditions simulated in the GCMs lead to changes in precipitation characteristics. Higher precipitation amounts are simulated in fall, winter and spring, while in summer, precipitation increases in northern Fenno-Scandinavia and decreases in the southern parts of the domain. Both daily and sub-daily intense precipitation over Fenno-Scandinavia become more frequent at the expense of low-intensity events, with most pronounced shifts in summer. In the Scandinavian mountains, pronounced changes occur in the snow climate with a shift in precipitation falling as snow to rain, reduced snow cover and less days with a significant snow depth. HCLIM at 3-km grid spacing exhibits systematically different change responses in several aspects, e.g. a smaller shift from snow to rain in the western part of the Scandinavian mountains and a more consistent decrease in the urban heat island effect by the end of the 21st century. Most importantly, the high-resolution HCLIM shows a significantly stronger increase in summer hourly precipitation extremes compared to HCLIM at the intermediate 12-km grid spacing. In addition, an analysis of the statistical significance of precipitation changes indicates that simulated time periods of at least a couple of decades is recommended to achieve statistically robust results, a matter of important concern when running such high-resolution climate model experiments. The results presented here emphasizes the importance of using “convection-permitting” models to produce reliable climate change information over the Fenno-Scandinavian region.

1 Introduction

Assessment of potential climate change impacts and the development of adaptation strategies to mitigate those impacts require reliable and trustworthy climate information at a wide range of spatio-temporal scales, from seasonal to sub-daily time scales as well as from regional to local spatial scales, even including information of changes within individual cities (Lu 2011; Koutroulis et al. 2015). Indeed, there is an increased need for more detailed, “actionable” climate information from impact researchers, stakeholders and policy makers for regional-to-local climate change assessments, which constitutes a strong incentive to perform higher-resolution climate projections (Gutowski et al. 2020; Hewitt et al. 2021). Currently, the most extensive set of high-resolution climate change projections for Europe originates from the EURO-CORDEX initiative where regional climate models (RCM) have been operated at 12.5 km grid spacing for Europe (Jacob et al. 2020). A large number of simulations exist and it has been shown that the RCMs can represent many features of the observed climate in a realistic way (Vautard et al. 2021). Climate change information from RCMs is detailed and provides information for assessing also uncertainties in future climate change on a European scale (Christensen and Kjellström 2020, 2021; Coppola et al. 2021).

Forced by an enhanced greenhouse effect, climate models project future warming that is more pronounced in northern Europe, including Fenno-Scandinavia, than the global average (e.g. Kjellström et al. 2018; Christensen and Kjellström 2018; Christensen et al. 2019, 2022). This is driven to a large extent by strong and positive feedback processes involving reduction of snow and ice as the climate warms (Previdi et al. 2021) further reinforced by a stronger lapse-rate feedback due to the strong warming of the surface (Boeke et al. 2021). Average precipitation amounts are also projected to increase, especially in winter, while in summer models typically show increases in northern and decreases in southern parts of Fenno-Scandinavia (Christensen and Kjellström 2018; Coppola et al. 2021). Along with mean changes, heavy precipitation events and summer warm extremes are commonly projected to increase in frequency and intensity (Nikulin et al. 2011). Anticipated changes in temperature, precipitation amounts, snowpack and snow cover under global warming will considerably impact surface energy and water budgets. This includes hydrological processes involving, for example, changed surface runoff as well as timing and amplitude of the spring flood (von Storch et al. 2015).

Even if regional high resolution downscaling is expected to improve many aspects of simulated climate (Liang et al. 2008; Paeth and Mannig 2012), the representation of large scales in the driving global climate model (GCM) can be a limiting factor (Hall 2014). If the large scales are not skillfully represented, then the potential for added value in the regional downscaling can be limited since errors in the large scales will in principal not be corrected (Kjellström et al. 2011). Similarly, in the climate change context, the RCMs produce climate change signals that are, to varying degrees, influenced by the climate change signal of the parent GCM (Christensen and Kjellström 2020; Sørland et al. 2018). Even with well-reproduced large-scale fields, coarser-scale models (with grid spacing of at least a few tens of kilometers) are not suited to provide regional details and represent smaller scale processes with high confidence (Palmer and Stevens 2019). Especially, future changes in precipitation distributions are still uncertain due to the difficulty of simulating certain aspects of precipitation processes such as atmospheric deep convection, sub-cloud dynamics and cloud microphysics (e.g. Lucas-Picher et al. 2021; Kendon et al. 2017; Prein et al. 2015). In recent years, with the increase in computing power, climate simulations at grid spacings of only a few kilometers (< 5 km) have become feasible. These simulations do not need parameterizations of atmospheric deep convection and are therefore termed “convection permitting” simulations (Lucas-Picher et al. 2021; Prein et al. 2015), and references therein). Climate simulations using convection permitting regional models (CPRCMs) have shown superior performance in simulating important aspects of climate, in particular precipitation including extremes (Kendon et al. 2012; Prein et al. 2015) and they also give partly different climate change signals compared to coarser-scale RCMs (Kendon et al. 2014, 2017; Lenderink et al. 2019). Improvements in reproducing observed precipitation distributions have been shown to result from more realistic representation of deep convective clouds such as meso-scale convective systems (Prein et al. 2017), and have led to improved simulation of sub-daily high-intensity precipitation events (Ban et al. 2014; Lind et al. 2016; Kendon et al. 2017) and better resolved diurnal cycle of precipitation (Leutwyler et al. 2017; Gao et al. 2017). Similarly, for the Fenno-Scandinavian region Médus et al. (2022), Belušić et al. (2020) and Lind et al. (2020) show that a CPRCM outperforms and adds value in the historical climate compared to an RCM operated at the standard EURO-CORDEX resolution. This was seen on local and regional scales both for sub-daily high-intensity precipitation events and the diurnal cycle of precipitation. With the finer grid meshes, CPRCMs better resolve surface characteristics such as coast lines and steep terrain and are therefore potentially more skilful in simulating weather and climate features in areas of complex terrain (Lucas-Picher et al. 2021), for example orographic precipitation (moist air that is lifted as it moves over a mountain range). Indeed, CPRCMs have been shown to better represent spatial distributions and intensities of precipitation as well as snow pack and snow cover in mountainous regions compared to coarser resolution models (e.g. Rasmussen et al. 2014; Ikeda et al. 2010; Liu et al. 2016; Adinolfi et al. 2020; Lüthi et al. 2019). Model uncertainties still adhere to CPRCMs that could be addressed in multi-model ensembles. However, due to the very high computational cost of running CPRCMs, their use in ensembles has only just recently started to emerge (Coppola et al. 2020). The expected increase in high-intensity precipitation events poses one of the main societal challenges of climate change in Fenno-Scandinavia (SOU 2007), stimulating the application of CPRCMs to assess future climate in this region and explore their benefits.

In this study we have performed a suite of climate simulations within the Nordic Convection Permitting Climate Projections project (NorCP; Lind et al. 2020), applying the HARMONIE-Climate (HCLIM) model cycle 38 (HCLIM38; Belušić et al. 2020) at 3 and 12 km horizontal grid spacing. Using two GCMs with climate change signals of different magnitude over northern Europe to provide lateral boundary conditions, we seek to provide insight to what extent a state-of-the-art CPRCM provides different and possibly more realistic climate projections compared to traditional coarser-resolution GCMs and RCMs over the Fenno-Scandinavia region. We also aim to identify when and where results are robust across resolutions by comparing to the forcing GCM and RCM that provides the boundary conditions for the CPRCM.

2 Methods

2.1 Models and experimental setup

The high computational cost of running HCLIM with a grid mesh size on kilometer scale (convection-permitting scales) limits the possibilities to investigate a wide range of possible model responses through an ensemble approach. Instead, another approach has been adopted here by making a well informed selection of a smaller number of forcing GCMs that have different responses over the target domain, Fenno-Scandinavia in northern Europe. Through this approach, two GCMs have been selected for dynamical downscaling, using two Representative Concentration Pathway (RCP) emissions scenarios RCP4.5 and RCP8.5 (Moss et al. 2010) and three time slices; 1985–2005 (historical period, from here on CTRL), 2041–2060 (mid-century, from here on MC) and 2081–2100 (late-century, from here on LC). RCP8.5 is a high emission scenario, entailing strong global warming by the end of this century, not least over northern Europe. It should be noted that RCP8.5 has been considered to be less plausible than lower emission scenarios (such as RCP4.5) given the recent developments and actions to reduce emissions as well as pledges for the future (see e.g. Hausfather et al. 2020). However, even with less plausibility, it is still of interest to investigate the climate responses to such high warming levels that furthermore cannot be fully ruled out. The two selected GCMs are EC-EARTH (Hazeleger et al. 2010, 2011) and GFDL-CM3 (Griffies et al. 2011; Donner et al. 2011). EC-EARTH and GFDL-CM3 have $1.125^\circ \times 1.125^\circ$ and $2.0^\circ \times 2.5^\circ$ atmospheric grid spacings respectively (latitude $\times$ longitude). The GCMeval tool (Parding et al. 2020) was used to compare GCMs from the CMIP5 ensemble (Taylor et al. 2012) and to guide in the selection of relevant GCMs. Figure 1 shows the end-of-century climate change signal (in the RCP8.5 emission scenario) in annual mean precipitation and near-surface temperature (T2m) over northern Europe in CMIP5. GCMeval uses the IPCC AR5 reference regions defined in Christensen et al. (2014) (see http://www.ipcc-data.org/guidelines/pages/ar5_regions.html), and northern Europe includes Fenno-Scandinavia, parts of the north-eastern Atlantic and the British Isles. Data from the CMIP6 (Eyring et al. 2016) ensemble with SSP5 8.5 scenario (Riahi et al. 2017) is included as well in Fig. 1, however these models were not available for selection at the start of the NorCP project and thus are only included here for reference. EC-EARTH (black diamond in Fig. 1) shows a warming of nearly 4 $^\circ$C and an increase of precipitation of about 0.2 mm/day, a response that is close to the CMIP5 ensemble mean (roughly a “middle-of-the-road” response). In contrast, GFDL-CM3 (green diamond in Fig. 1) shows a stronger annual mean change in both precipitation and T2m compared to EC-EARTH; around 5.5 $^\circ$C warming and 0.5 mm/day increase in precipitation. In addition, GFDL-CM3 has a larger and more rapid decrease in sea-ice cover over the Arctic in the 21st century (Massonnet et al. 2012), a factor that can potentially have important consequences in surrounding areas (Cohen et al. 2014, 2021; Overland et al. 2016; Screen et al. 2015), including northern Europe and Fenno-Scandinavia.

Fig. 1

GCM model responses of annual mean near-surface temperature (x-axis) and daily precipitation (y-axis) over northern Europe for the CMIP5 and CMIP6 ensembles. The data points represent the differences between historic period (1980–2005) and end-of-century (2071–2100). The two selected CMIP5 GCMs are marked with a black (EC-EARTH) and green (GFDL-CM3) diamond respectively

The selected GCMs are dynamically downscaled with the HARMONIE-Climate regional climate model. For this study cycle 38 (HCLIM38) was used which has been thoroughly described in Belušić et al. (2020). Due to limited computer resources, however, only one of the selected GCMs (EC-EARTH) was downscaled for the RCP4.5 emission scenario. Two sets of configurations of HCLIM38 were used here (Fig. 2); one using the ALADIN physics package (Termonia et al. 2018) and a domain covering most of Europe with 12 km grid spacing (hereafter HCLIM12); and one using the HARMONIE-AROME physics package (Bengtsson et al. 2017; Seity et al. 2011) applied at an inner domain covering Fenno-Scandinavia with 3 km grid spacing (hereafter HCLIM3). In HCLIM12 atmospheric convection is parameterized while in HCLIM3 atmospheric deep convection is treated explicitly by the model itself. Except for the forcing data and time periods the experiment configurations are the same as in Lind et al. (2020) where the reader can find further experiment details, and more detailed physics descriptions can be found in Belušić et al. (2020).

Fig. 2

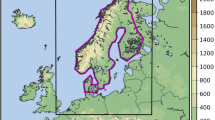
Domain used in the HCLIM12 simulations. The nested HCLIM3 domain is represented by the inner blue rectangle. The color scale represents the altitude above mean sea level in meters. The dashed-line magenta colored box defines the Fenno-Scandinavia sub-domain used in the analysis, and the solid-line magenta polygon over southern Norway is the area used in the Scandinavian mountains analysis in Sect. 3.3.3. The cities (red dots and names) are used in the urban heat island (UHI) index calculation in Sect. 3.3.4

2.2 Analyses

2.2.1 Data

In Sect. 3.1 the model data is compared to both the HCLIM12 and HCLIM3 hindcast experiments (i.e. ERA-Interim reanalysis driven simulations, presented in Lind et al. (2020) as well as the ERA5 reanalysis (Hersbach et al. 2020). For this purpose all data have been interpolated to the ERA5 grid prior to analysis (grid spacing in ERA5 is $\sim$31 km), except in Fig. 3 where ERA5 and EC-EARTH data is interpolated to the GFDL grid. Precipitation is interpolated conservatively while for all other variables a bilinear method is used. In the rest of the sections, where we investigate the future responses of each model and whether these deviate systematically between the models, the data is kept on their native grids (unless otherwise stated).

2.2.2 Statistical significance

Since producing decadal-long CPRCM simulations are computationally still very demanding, constraining their use in longer-term and/or in ensemble modeling efforts, we test in Sect. 3.2.3 the sensitivity of the simulated climate change to the length of time period (number of years/seasons). To this end climate change signals are first tested for significance using standard Student’s t-tests (von Storch and Zwiers 2002). It is applied to each grid point separately in the analyzed domain (see Fig. 2) and the fraction of grid points where the null-hypothesis (i.e. no change) can be rejected at the 95% confidence level is calculated. Secondly, we randomly sub-select years from the original simulations to create 5-year and 10-year long time periods, for both CTRL and scenarios, and test similarly for significance in the future changes. The selection of each sub-period is performed in a bootstrap fashion, creating a large number of sub-periods (here 400 samples), resulting in distributions of fractions (of domain grid points) with statistically significant changes. These 5 and 10 year distributions are presented in box plots together with the single fraction obtained by using all 20 years.

2.2.3 ASoP

The “Analyzing Scales of Precipitation” (ASoP) method (Klingaman et al. 2017; Berthou et al. 2018, 2019) is applied to analyze the full range of simulated precipitation intensity distributions, both on daily and hourly time scales. ASoP involves splitting the total mean precipitation into contributions of different rates, both in an absolute and relative sense referred to as actual and fractional contributions respectively. This is achieved in a few steps: First, precipitation distributions are separated into discrete bins of different precipitation intensities. These bins are defined so to ensure that each bin contains a similar number of events, i.e. to account for the disproportionately higher frequency of low-intensity precipitation events compared to high-intensity events. In this study an exponential bin distribution described in Berthou et al. (2019) is used. In the second step, the actual contribution (in millimeters) of each bin to the total mean precipitation rate is obtained by multiplying the frequency of events by its average rate. The sum of the actual contributions from all bins gives the total mean precipitation rate. The fractional contribution (in percent) of each bin is further obtained by dividing the actual contributions by the total mean precipitation rate (whereby the sum of all fractional contributions is equal to 1), essentially providing information about the shapes of the distributions.

2.2.4 Synoptic activity

A simple diagnostic described in Harvey et al. (2020) is used to estimate the large-scale circulation and occurrences of low-pressure systems over northern Europe. The method involves filtering mean sea-level pressure (MSLP) fields using a band-pass filter with cut-off frequencies appropriately defined to retain variability on synoptic time scales (Harvey et al. 2020). In this study daily mean MSLP data are used and each time series (per grid point) is 2–6 day bandpass-filtered using a 61-day Lanczos filter (Duchon 1979), in other words MSLP variability occurring on time scales between 2 and 6 days is retained. After filtering the standard deviation is calculated (per grid point) giving the measure of what is called here “synoptic activity” (SA) in units of hPa. The analysis is performed both on the models native grids and on the ERA5 grid (in Sect. 3.1), and for each season separately. We also used 6 h MSLP data from the HCLIM models, however, since the 6 h and daily results are very similar only results using daily values are included here.

3 Results and discussions

3.1 Evaluation of retrospective experiments

Even though the main focus of this study is on the simulated climate change over Fenno-Scandinavia, it is of interest to have at least a basic understanding of how the models perform for the recent past compared to observations or reanalysis data. Not least with respect to the performance of the GCMs since they provide the boundary conditions to HCLIM, but also to provide context for the climate change signals. In this section we briefly discuss the results from control experiments (CTRL) over the time period 1986–2005 comparing to ERA5 reanalysis data (Hersbach et al. 2020). We acknowledge that this is a relatively short time span (climatologically) that prevents a more robust analysis; for example, although the GCMs use observed forcings in the control experiments, decadal and/or multi-decadal internal climate variability occurring in the models may be out-of-phase with the observed variability. This can cause apparent large differences in climate fields that would otherwise not be as large if averaging over a longer time span. However, it should also be noted that the simulated 20-year time periods are twice as long as the typical length of CPRCM simulations in the majority of previous studies (Pichelli et al. 2021; Berthou et al. 2019; Dai et al. 2017; Kendon et al. 2017).

Fig. 3

Winter (DJF) and summer (JJA) averages over the control period (1986–2005) of daily mean sea-level pressure (contours) and synoptic activity (SA, color shading) in ERA5 (leftmost panels) and the differences in EC-EARTH (middle) and GFDL (right) with respect to  ERA5. Units in hPa. ERA5 and EC-EARTH data have been interpolated to the GFDL grid prior to analysis. The full fields of EC-EARTH and GFDL are presented in Fig. S1 of Supplementary material

Fig. 4

Seasonal differences with respect to ERA5 over Fenno-Scandinavia region for: (a) synoptic activity (SA); (b) daily mean T2m; and (c) daily precipitation. Data has been averaged over the 1986–2005 time period so that each box and whisker represents the spatial (grid point) distribution of differences over the target domain. HCLIM12 and HCLIM3 forced by ERA-Interim reanalysis for the 1998–2018 time period have also been included for reference (cyan and purple colored boxes respectively). The central line in the boxes is the median value and whiskers show the 5th and 95th percentiles

Figure 3 shows the large-scale circulation over the North Atlantic and Europe in ERA5 and the GCMs as represented by multi-year average of daily mean sea-level pressure (MSLP) and synoptic activity (SA, see Sect. 2.2.4). In winter (December-January-February; DJF), EC-EARTH and GFDL show similar dipole patterns of differences with respect to ERA5 characterized by too low synoptic activity over the Nordic seas and northern Europe and similar or too high activity compared to ERA5 near the British Isles and over mid- and south Europe. This is an indication of an overestimation of the zonal flow strength which is commonly seen in CMIP5 GCMs over the historic period (e.g. Harvey et al. 2020). In summer (June-July-August; JJA) the storm track is weaker compared to winter. In the GCMs the synoptic activity is weaker still compared to ERA5 over large parts of the North Atlantic, while being stronger over continental Europe, particularly in GFDL in southern and eastern Europe. As with winter this is in line with the general performance of CMIP5 GCMs (Harvey et al. 2020).

In Fig. 4 differences in SA, T2m and daily precipitation (Pr) over Fenno-Scandinavia (see Fig. 2) compared to ERA5 are summarized in box plots for all seasons. The figure reveals clear differences between the two GCMs as well as between the GCMs and HCLIM, and these differences concern both average values and spatial variability. In DJF both GCMs and HCLIM underestimate SA with larger deviations in GFDL runs. HCLIM forced by GFDL has around 15% lower SA compared to ERA5. In JJA SA is in closer agreement with ERA5, mostly within +/- 5%, and HCLIM has lower biases compared to forcing GCMs. In the intermediate seasons (spring, March-April-May (MAM); and autumn, September-October-November (SON)) the performances of the GCMs deviate from each other; in MAM EC-EARTH simulations show larger underestimation of SA compared to GFDL simulations, while vice versa is seen for SON. HCLIM models generally follow the response of the corresponding forcing GCM, however, the GFDL driven runs have consistently lower SA than GFDL rendering stronger underestimations compared to ERA5 in DJF and SON. The reason for the systematicllay lower SA values in HCLIM, also seen in the climate change signals (see Sect. 3.2.1), is not clear at this stage. The much coarser grid spacing in GFDL ($\sim$200 km) compared to HCLIM could mean less ability to represent the topographic influences on the atmospheric flow (Sandu et al. 2019), in Fenno-Scandinavia imposed by the Scandinavian mountains (Scandes). However, it is still not clear if and to what extent higher grid resolution, and/or model physics like orographic drag, can reduce biases in the large-scale circulation typically seen in coarse-scale climate models (e.g. Pontoppidan et al. 2019). The hindcast simulations (forced by ERA-Interim), although covering a sligthly different time period (1998–2018), show overall better agreement with ERA5 (median values closer to zero and less spatial spread). Still, the hindcast simulations exhibit a systematic underestimation of SA in DJF and SON, and in the latter the EC-EARTH simulations actually perform better.

All models simulate on average lower T2m over Fenno-Scandinavia than ERA5 (Fig. 4b), particularly in JJA, however, in DJF the median values are in closer agreement with ERA5. The cold bias in HCLIM is to a large extent inherited from the forcing GCMs, as the hindcast simulations show smaller biases with respect to ERA5 (Fig. 4b). Still, the bias distributions in HCLIM are indicating mostly lower temperatures than in GCMs, and these colder conditions have been recognized in the hindcast simulations when compared to other observational data sets (Lind et al. 2020).

In terms of precipitation the median values of EC-EARTH are lower than ERA5 in all seasons, with the most negative difference in JJA which is also the case for GFDL (Fig. 4c). In DJF and SON, on the other hand, GFDL exhibits larger median values. HCLIM3 simulates lower amounts of precipitation than HCLIM12 and the GCMs in almost all seasons, being particularly dry in MAM and JJA, although in JJA HCLIM3-GFDL shows similar (spatial) bias distribution as GFDL. It is also noteworthy that in JJA HCLIM12 has larger amounts than both HCLIM3 and GCMs and thereby being closer to ERA5. This is also seen for the hindcast simulations, where HCLIM3 has lower precipitation amounts in JJA (as well as in the other seasons) compared to HCLIM12 and ERA5 (Fig. 4c). However, it was also shown in Lind et al. (2020) that JJA precipitation in HCLIM3 was in much closer agreement with high-resolution observational data over Fenno-Scandinavia (considering only land areas), HCLIM12 and ERA5 being overly wet in this season. We further note that, apart from JJA, GFDL shows a significantly larger spatial spread in the biases (given by the extent of the boxes and their whiskers), to some extent reflected in the HCLIM-GFDL simulations. This is consistent with, and potentially in part a consequence of, the larger spread in GFDL than in EC-EARTH simulation seen for the synoptic activity (SA, Fig. 4a).

3.2 Time mean climate change

Average future responses for MC and LC periods in the RCP4.5 (only EC-EARTH simulations) and RCP8.5 scenarios on seasonal time scales are summarized in Figs. 5 and 6. Whereas thermo-dynamic climate responses, for example atmospheric warming and moistening, generally are well understood, potential modifications in atmospheric dynamics, especially on the regional to local scales, are much less certain (e.g. Shepherd 2014) especially in the Euro-Atlantic region (Woollings 2010). Dynamical influences on regional climate change patterns and magnitudes may nevertheless be important and simulated changes in surface pressure fields are therefore a useful starting point in the analysis.

Fig. 5

Seasonal changes over Fenno-Scandinavia with respect to control period (1986–2005) in; (a) synoptic activity (SA); (b) daily mean T2m; and (c) daily precipitation. The time average is calculated over each time period, and each box and whisker distribution represents grid points over the target area. The annotation above DJF $\Delta$SA shows how respective future time periods (MC; 2041–2060 and LC; 2081–2100) are divided between the boxes. Solid and dotted line styles for boxes and whiskers represent RCP8.5 and RCP4.5 respectively. Box and whisker definitions as in Fig. 4

3.2.1 Mean sea-level pressure

As expected, the GCM simulated changes in seasonal large-scale circulation over Fenno-Scandinavia, represented by synoptic activity (SA), are only marginally modified by the HCLIM models (Fig. 5a). In contrast, larger differences are seen between the GCMs, scenarios and time periods in the simulated changes in SA (see also Fig. 6). In DJF and SON (and MAM in the LC period) the sign of change of median values are different in the GCMs, negative in EC-EARTH (about 5–10% decrease in LC) and positive in GFDL (around 10–15% increase in LC). We note, however, that the SA change signals are more strongly modified by HCLIM in GFDL forced simulations compared to the ones forced by EC-EARTH, manifested as a notably smaller SA increase in DJF, MAM and SON, and a larger decrease in JJA in HCLIM compared to GFDL.

The temporal changes are in some cases different. For example in RCP8.5, EC-EARTH projects an increase in SA in MAM (in the median value) by MC followed by a decrease by LC whereas in RCP4.5 EC-EARTH shows decreases in both time periods. Also in JJA the simulations show different trends in the signals, however, by LC all models show a decrease on average with the strongest decrease in HCLIM-GFDL simulations. All in all, keeping in mind the large temporal variability, the amplitude of the changes by LC are mostly within 5–10%. While EC-EARTH simulates a decrease of approximately 2–10% in SA throughout the year, GFDL projects an increase of larger magnitude in DJF, MAM and SON of around 10–15% (with somewhat smaller increases in HCLIM-GFDL). The opposite changes in these seasons between the GCMs will evidently impact inter-model differences in other climate variables as well.

Figure 6 shows the spatial changes for the RCP8.5 scenario in DJF and JJA circulation in LC, as well as for other variables, in HCLIM12. In DJF both HCLIM12-GCM combinations simulate reduced average MSLP pressure over parts of Scandinavia and the Nordic seas, and an increase over continental Europe and British Isles, which suggests increased zonal flow. The dipole change pattern is particularly strong in HCLIM12-GFDL and is in agreement with the increased SA over North Atlantic and Fenno-Scandinavia while HCLIM12-ECE instead shows negative or very small changes (see also Fig. 5a). In JJA the most prominent change is the increase in MSLP in a cell-structure centered over or just west of British Isles and extending in over continental Europe, suggesting an expanding or intensifying Azores high and is associated with a reduction in SA (Fig. 5a).

Fig. 6

HCLIM12 winter (a) and summer (b) seasonal average differences between LC in RCP8.5 and CTRL experiments. Left column: Synoptic activity (SA; shading) and MSLP (contours), both units in hPa; middle column: T2m (shading, in °C) and near-surface specific humidity (Q2m; contours, in %); right column: Precipitation (percent change per degree warming, both shading and contours)

3.2.2 Temperature, near-surface humidity and precipitation

2-metre temperature (T2m) increases almost linearly in all models and seasons from CTRL to MC and LC periods (Fig. 5b). As seen in Fig. 6a, the warming in DJF is most pronounced (above 7 °C warming) in oceanic regions close to the Arctic as well as over northern Fenno-Scandinavia and Russia mostly due to reduced snow, ice and sea-ice cover (this is also seen in Fig. 5 where the spread in the spatial responses increases from MC to LC). These areas also exhibit the largest relative increase in near-surface specific humidity (Q2m; contour lines overlying the temperature field in Fig. 6). The temperature changes are more strongly enhanced in GFDL runs than in EC-EARTH runs; in particular the warming in JJA is around 2–3 $^\circ$C larger in GFDL (Fig. 5b), not only over Fenno-Scandinavia but also over large parts of Europe (Fig. 6b). In GFDL the strongest warming occurs in JJA (Fig. 5b), even exceeding the increase in DJF, which is in stark contrast to EC-EARTH that has the smallest increase in JJA. There is no clear impact of HCLIM12 and HCLIM3 on the seasonal average T2m changes, although both HCLIM-GFDL simulations exhibit lower increases than GFDL in MAM, JJA and SON for both MC and LC time periods.

Daily precipitation (Pr) increases on average in DJF, MAM and SON, already in MC but most clearly in LC when almost all grid points in target domain show increases (Fig. 5c). GFDL simulations have the strongest increase, most pronounced in DJF and SON with median values around +40% in LC in RCP8.5 (with even larger increases in HCLIM12-GFDL and HCLIM3-GFDL). Spatially, the larger increase in DJF Pr in HCLIM12-GFDL compared to HCLIM12-ECE is seen mainly over Fenno-Scandinavia, the North Sea and over the British Isles and is consistent with the intensified zonal flow and higher synoptic variability (SA) in this area (Fig. 6a). Note that in Fig. 6, Pr changes are shown as rates of increase per degree warming; the combination of higher rates of increase and larger warming in HCLIM12-GFDL compared to HCLIM12-ECE results in significantly larger total increase in winter precipitation amounts (Fig. 5c). In JJA, even though the median change is positive in most models and time periods (RCP4.5 MC has median values close to zero), the change signals include decreases in some parts of Fenno-Scandinavia (as depicted by the box distributions extending into negative change values). The spatial spread of the responses also becomes larger by the end of the century with decreases of Pr mostly occuring in southern Fenno-Scandinavia and increases in the northern part. This is also evident from Fig. 6b, which shows that the increase in MSLP and corresponding decrease in SA are associated with a decrease in Pr in many parts of Europe, including parts of southern Fenno-Scandinavia. Both HCLIM12-GFDL and HCLIM12-ECE show similar change patterns which also include increased Pr amounts over the Nordic seas and northern Fenno-Scandinavia (Fig. 6b). Consistent with the enhanced summer warming in GFDL compared to EC-EARTH, the relative increase in Q2m is enhanced in HCLIM12-GFDL by 20–30% points compared to HCLIM12-ECE (Fig. 6b), close to the expected difference as given by the Clausius–Clapeyron relation (approximately 7%/$^{\circ }$C). Indeed, the increase in Q2m in summer over Fenno-Scandinavia and northern Europe is not generally limited by moisture availability, while this is the case in mid- and south Europe; the stronger warming seen there is not accompanied by a larger increase in Q2m and precipitation decreases more strongly (Fig. 6b).

3.2.3 Statistical significance of simulated changes

How significant are the simulated changes seen in Fig. 5? The increase in T2m is seen in all grid points of the analyzed domain, with the lowest warming in JJA by mid-century in RCP4.5 scenario of 1–2 $^{\circ }$C. In contrast, the change signal for Pr is more uncertain with generally larger spatial spread (given by the spread of distributions in Fig. 5c) and also the sign of change varies, particularly in JJA. Here we test the robustness of the climate change signal for T2m and Pr (see Sect. 2.2.2). Further, considering the high demand for resources running CPRCM models, one might ask what is the minimum length of time periods needed to be simulated to be able to detect statistically significant change signals? Thus, we also investigate the sensitivity to the length of considered time period. The results are summarized in Fig. 7 showing the fraction of all grid points over Fenno-Scandinavia that exhibit statistically significant changes for daily mean and maximum (based on hourly data) Pr. The same analysis was performed for daily minimum and maximum T2m and nearly all results showed statistically significant warming over the whole domain and thus were not included in Fig. 7.

For daily mean Pr (Fig. 7a) there are mostly small fractions in the RCP4.5 scenario, both in DJF and JJA, only occasionally reaching 50% (most frequently in DJF). There are also no clear differences between 5 and 10 year periods. For RCP8.5 the two seasons show larger differences. In DJF, when the models exhibit widespread increase in Pr amounts (Fig. 5c), changes become more significant, and by end-of-century (“RCP85 LC”) 10 year time periods as well as the full 20 year period in GFDL driven simulations have significant changes in 90–100% of the grid points. The sensitivity to the length of the time period can still be large. For example, for GFDL at MC and EC-EARTH at LC the fraction of significant grid points (median value of all sub-periods) is around 50%, 70% and 90% for the 5, 10 and 20 year periods, respectively. In JJA, on the other hand, the significance is still limited to mostly below 50% of the domain. In both seasons, there is a large sensitivity to length of considered time period, i.e. a greater fraction of significant changes occurs when using 10 instead of 5 years.

For daily maximum Pr (Fig. 7b) the degree of significant changes increases (compared to daily mean) in most simulations and scenarios. One outstanding example is HCLIM3-GFDL in RCP8.5 LC in JJA; the fraction of significant changes in 10-year periods increase (referring to the median value of the distributions) from $\sim$40% for daily mean to $\sim$65% for daily maximum Pr. It is also noteworthy that, in JJA, there are more significant changes in HCLIM3 than in HCLIM12 unlike the case for daily mean Pr.

These results indicate that the significance of Pr changes is rather sensitive to the length of considered time period, where the full 20-year periods in most cases show higher degree of significance than 5 and 10-year periods. As seen in Fig. 7 statistically significant Pr changes can be difficult to detect at MC, however, even at LC for RCP8.5 (with very strong warming signal) the degree of significance can be low, especially for 5-year periods but also for some 10-year periods. This implies that it is advisable, at least based on this analysis, to consider 10-year time periods at a minimum (in line with the discussion of Ban et al. (2015)) but preferably longer periods, spanning at least 20 years.

Fig. 7

Fraction of grid points over Fenno-Scandinavia that have statistically significant changes for a daily mean and b daily maximum Pr. Each box distribution is based on sub-sampling 5 and 10 year periods from the original simulations 400 times, each sub-period tested for significance that in the end provides an estimate of fraction of grid points. The magenta colored star between each pair of 5 and 10 year distributions is the corresponding fraction if all 20 years is used. The number above each box is the percentage of all grid points with significant changes that are positive

3.3 Climate signal modulation from GCM to CPRCM

The focus of this section is to assess in more detail systematic differences and similarities, and potentially indications of convergence, in the climate change responses between the GCMs, HCLIM12 and HCLIM3. There is widespread appreciation and evidence of  improved representations of various aspects of the climate system through the continual refinement of the grid mesh in climate models, most consistently for precipitation (Gutowski et al. 2020; Rummukainen 2015; Demory et al. 2020; Strandberg and Lind 2021), recently also seen over Fenno-Scandinavia (Médus et al. 2022; Lind et al. 2020). However, even though improvements are seen in high-resolution models for the present climate, they do not necessarily provide additional information, or systematically different responses, in the change signals of future climate projections (Rummukainen 2015; Di Luca et al. 2015; Kendon et al. 2017).

Added value of very high-resolution models is also expected in areas of complex terrain. In recent years, both observations and model simulations of present and future climates have suggested an emergent pattern of regional climate change in mountainous regions called elevation dependent warming (EDW) (Li et al. 2020; Palazzi et al. 2018; Pepin et al. 2015). EDW manifests as an increasing rate of warming with altitude, driven primarily by factors such as reduced albedo (less snow cover), increased down-welling thermal radiation and near-surface specific humidity (e.g. Palazzi et al. 2018). Larger rates of temperature changes in mountainous areas in the future can have important implications for changes in the cryosphere with further impacts on runoff, water availability and distributions. With the complexity and heterogeneity of mountainous regions, model grid resolution is an important factor to accurately represent mountainous climates. Recent literature has shown that greenhouse gas-forced climate responses in mountainous regions can only be accurately captured by models having a horizontal grid spacing of 5 km or less (Pepin et al. 2015; Rasmussen et al. 2011), suggesting a potential benefit of HCLIM3 responses over the Scandes (the Scandinavian mountain range) compared to HCLIM12. This is briefly investigated here in Sect. 3.3.3.

Fig. 8

The scatter plots show differences between LC and CTRL RCP8.5 experiments for (a), (b) temperature (T2m), (c) precipitation (Pr) and (d) daily average 10 m horizontal wind speed (U10). Squares represent GFDL experiments (GCM and corresponding HCLIM12/HCLIM3 downscalings) and circles EC-EARTH experiments. Colors represent DJF (blue) and JJA (red) seasons. The max/min subscripts refer to daily maximum and minimum values and Ann max/min is the annual maximum/minimum value averaged over the 20-year time periods. sdii is the simple daily intensity index calculated for precipitation.

3.3.1 Changes in averages versus minimum and maximum values

Figure 8 shows the DJF and JJA climate change responses (LC minus CTRL) for RCP8.5 in GCMs and HCLIM over Fenno-Scandinavia for T2m, precipitation and 10 m horizontal wind speed (U10). Corresponding results for MAM and SON are presented in Figure S2 in Supplementary. The GFDL/HCLIM-GFDL simulations experience a stronger summer warming than EC-EARTH/HCLIM-ECE simulations of about 3 $^{\circ }$C (with a total warming of around 7 $^{\circ }$C) (Fig. 8a, b). In JJA the change in daily maximum and minimum temperatures is similar to the change in daily mean temperature. In DJF, on the other hand, the overall warming in daily mean T2m is dominated by the increase in daily minimum temperatures (also evident in SON and MAM, see Fig. S2). This is commonly seen for northern Europe in a warming climate mainly due to retreating snow and ice-cover and reduced occurrences of situations with very low temperatures (Christensen and Kjellström 2018; Nikulin et al. 2011).

Figure 8c shows that while the overall intensity of Pr, given by the simple daily intensity index (sdii; calculated as the average of all wet days, i.e. days with at least 1 mm of precipitation), is increasing in both seasons, the annual maximum one-day Pr amount (averaged over the simulated 20-year time periods) increases at a larger rate (values above the one-to-one line in Fig. 8c). This response is more clearly visible for JJA than in DJF, while in SON and MAM the response is stronger in GFDL than in EC-EARTH simulations (Fig. S2). The simulated larger increase of extreme Pr than mean Pr in response to warming is a remarkably robust result projected in many other models and regions (Fischer et al. 2013; Li et al. 2019).

Future changes in 10 m wind speed over northern Europe are associated with large uncertainties, often weak change signals and large inter-model spread in the responses (Tobin et al. 2016; Kjellström et al. 2011; Nikulin et al. 2011). Nikulin et al. (2011) found slight increases in 10 m wind speed extremes over northern Europe, although with large spread between RCMs downscaled with different GCMs. Donat et al. (2011) also found increases in wind extremes over northern Europe but mostly limited to an area extending from the British Isles to the southern parts of Fenno-Scandinavia. As seen in Fig. 8d, there is no discernible difference in the response of seasonal mean and maximum 10 m wind speed (U10). Still, there are contrasting responses from the GCMs; EC-EARTH simulations show very small changes while GFDL simulations exhibit an increase in wind speed in DJF of around 5–10% and a decrease of similar magnitude in JJA. These responses are broadly consistent with results from the EURO-CORDEX RCM ensemble over this region (Christensen et al. 2022). The changes are also consistent with the increase and decrease in synoptic activity in DJF and JJA respectively (Figs. 5a and 6a). The increase in wind speed in GFDL GCM is regionally quite large, for example a $\sim$50% increase in both seasonal mean and maximum wind speed over northeastern Sweden, Bay of Bothnia and Finland in all seasons (not shown). Interestingly, this systematic change is strongly reduced in the HCLIM-GFDL simulations explaining the differences in change signals in Fig. 8d between GFDL and HCLIM. However, overall the HCLIM responses tend to be in close agreement with the forcing GCM, in line with the common outcome that uncertainties in wind speed and its changes are more related to the individual GCM (providing the large scale forcing) than between different RCMs (Kjellström et al. 2011; Moemken et al. 2018).

Indeed, an overall feature from Fig. 8 is that the HCLIM12 and HCLIM3 responses tend to cluster around the forcing GCM, a clear indication of the control the forcing GCM exerts on the responses from downscaling experiments. The spread between models (for a given GCM) is relatively larger for some parameters and variables, in particular JJA Pr (Fig. 8c) and U10 in the GFDL simulations (Fig. 8d). In a few other cases HCLIM12 and HCLIM3 converge to similar change values while clearly differing from the GCM, e.g. the smaller increases in DJF (Fig. 8b), MAM and SON (Fig. S2) daily minimum T2m and wind speed (the latter only in GFDL simulations).

3.3.2 Change in precipitation distributions and extremes

High-resolution models are not only able to show higher skill in reproducing the observed precipitation climate but potentially also more robust (and perhaps different) projections of precipitation changes in climate projections (Fosser et al. 2020; Kendon et al. 2017). Figure 9a shows the actual contributions to the total mean Pr per daily Pr intensity, computed from the ASoP analysis. In the present climate (CTRL experiments) HCLIM12 and HCLIM3 have larger contributions than the GCMs from daily intensities above around 10 mm/day and smaller contributions for intensities below 5 mm/day, essentially a shift of the distributions to higher intensitites (top panels in Fig. 9a). This is expected given the differences in horizontal grid spacing in the models (Demory et al. 2020; Strandberg and Lind 2021), further indicated in GFDL (with the coarsest grid mesh) that shows lower contributions compared to EC-EARTH from moderate-to-high (above ca 5 mm/day) and higher contributions from low (< 5 mm/day) intensities.

In both DJF and JJA all the models exhibit an increase in the RCP8.5 LC period (with respect to CTRL) in contributions from moderate (several mm/day, depending on the model) and higher intensities, with reduced contributions from lower intensities (bottom panels in Fig. 9a). The areas under the curves representing increases are generally larger than those for decreases which means an increase of the total mean Pr, most pronounced in DJF. Furthermore the changes are stronger in the GFDL downscalings. The changes in the fractional contributions (see Figure S3 in Supplementary) clearly show the shift to larger contributions from higher daily amounts (> $\sim$8–12 mm/d) and less from lower amounts. However, while the shifts in DJF are mostly similar between the models (albeit with some differences in magnitudes), in JJA there is a larger spread. As the model grid spacing is refined from GCM via RCM to CPRCM the crossover from decreases to increases in JJA fractional contributions occur at increasingly higher intensities (Fig. S3). The most pronounced change in JJA is seen in HCLIM3-GFDL with a clear decrease in both relative and actual contributions from precipitation rates less than around 13 mm/day and prominent increase for higher rates (Fig. 9a and Fig. S3).

Fig. 9

a ASoP actual contributions for DJF and JJA daily precipitation in GCMs and HCLIM models. Top panels show actual contributions for CTRL while lower panels show the changes in RCP8.5 by LC (i.e. LC-CTRL). b Percentiles of DJF and JJA daily precipitation in CTRL (top panels) and percentage changes in RCP8.5 (between LC and CTRL) normalized by local change in T2m (bottom panels). All data is used, including dry days, in calculation of percentiles

The late century climate changes (LC-CTRL) of high percentiles of daily Pr show a tendency of convergence for DJF with changes asymptotically approaching 4*–6%/$^{\circ }$C change for the highest percentiles ($\ge$ 99th) (Fig. 9b). In JJA the spread between the LC responses is larger with no clear convergence to a specific change value, rather the responses trend towards higher change rates  reaching between 6 and 9 %/$^{\circ }$C for the 99.99th percentile. In both seasons, HCLIM3 has the largest increase for the highest percentiles.

Fig. 10

As in Fig. 9 but for hourly data and only HCLIM12 and HCLIM3. Included here is also the RCP4.5 scenario in EC-EARTH driven runs (dotted lines)

Figure 10 shows that on the hourly time scale, even though the general features as seen for daily time scales are present at sub-daily time scales as well, more distinct differences appear between HCLIM12 and HCLIM3. In the CTRL experiments, HCLIM3 has lower peaks and larger contributions from high Pr intensities, both in DJF but particularly in JJA (Fig. 10a). Conversely, HCLIM3 has smaller contributions from low Pr intensities. In JJA, the bulk of the increase in HCLIM3 occurs around 8 mm/h while for HCLIM12 it occurs around 3 mm/h. There is also a stronger decrease in JJA of contributions from lower Pr rates in HCLIM3 (below about 1 and 3 mm/h in HCLIM12 and HCLIM3 respectively. See also corresponding changes in fractional contributions in Fig. S4), which results in lower JJA total mean Pr in HCLIM3-GFDL than in HCLIM12-GFDL for the LC period (cf Fig. 5c). The disparate responses in DJF and JJA between HCLIM12 and HCLIM3 is even further emphasized for the higher percentiles of hourly Pr (Fig. 10b). In winter, as for daily time scales, the models converge toward a specific value for the 99th percentile and higher rankings, and the HCLIM12 and HCLIM3 simulations forced by the same GCM follow relatively closely together. In JJA, in contrast, the distinction between HCLIM12 and HCLIM3 responses are very clear, HCLIM3 having stronger rates of changes for rankings above the 99th percentile. Further, the similar change rates in the two HCLIM3 and HCLIM12 runs respectively indicate a smaller GCM control on the responses in this season. The different behaviour between DJF and JJA is an important indication of the impact of model grid resolution and physics (in particular the handling of cloud and precipitation processes) on the change patterns; precipitation in DJF is mostly associated with large-scale features like low pressure systems and associated fronts while in JJA precipitation of smaller scale convective origin becomes more frequent. Similar conclusions have been drawn in other studies of CPRCMs. For example, Fosser et al. (2020) showed similar decrease in contribution from low-to-moderate hourly precipitation over the United Kingdom in a CPRCM and a RCM, with the CPRCM having a stronger increase for the highest intensities. They argued that the main reason for these results is the more realistic representation of atmospheric convection in the CPRCM, thus providing more reliable climate projections of precipitation, particularly extremes. Furthermore, changes in moisture availability can be an important limiting factor for how the nature of precipitation will change in a warming climate. In southern Europe the projected strong summer drying can lead to very muted increases in high-intensity precipitation events compared to other seasons like winter and autumn (Chan et al. 2020; Lenderink et al. 2019). Furthermore, in a pseudo-global warming experiment, Dai et al. (2017) investigated in a 4-km model simulation future changes in warm season precipitation characteristics over the United States. The authors concluded that the increase in frequency of high-intensity precipitation events at the expense of low-intensity events that occurred less frequently indicated an important change in the intermittent nature of precipitation. They found increases in dry periods between rain events suggesting that more time was needed between events to replenish moisture in the atmosphere, leading to conditions with fewer but more intense rainstorms (Dai et al. 2017). The decrease in average JJA precipitation seen here in southern parts of Fenno-Scandinavia with the concurrent increase in high-intensity daily and sub-daily precipitation is an indication of a similar effect, with a more pronounced signal in HCLIM3 compared to HCLIM12. Further separating the analysis of high percentiles in Fig. 10b into land and sea grid points (Fig. S5) shows that with a permanent source of surface moisture (over sea) the highest percentiles increase at a faster rate (> 10%/ $^{\circ }$C in HCLIM3) than over land, again more distinctly seen in HCLIM3 compared to HCLIM12. Lenderink et al. (2019) recently reported a similar dependence on moisture availability, and contrast between land and sea regions, for the rate of change in summer precipitation extremes in RCM and CPRCM models.

3.3.3 Changes in temperature and snow climate in the Scandes mountains

Figure 11 shows the seasonal changes in daily maximum (a–d) and minimum (e–h) T2m by the LC period in HCLIM12 and HCLIM3 as a function of orographic height over the southern part of the Scandes (the broadest area with steep orography and the highest peaks, see Fig. 2). The T2m-altitude profiles in the CTRL experiments, shown in Fig. S6 in Supplementary, are overall similar in HCLIM12 and HCLIM3. A notable exception is the colder HCLIM12 in DJF (and to a smaller extent in MAM and SON), most pronounced for daily minimum T2m and altitudes above 800 m, with around 1–2 $^{\circ }$C lower temperatures in HCLIM12 (Fig. S6). It is further noted that HCLIM3 exhibits less spread of the mean values leading to more well defined vertical profiles compared to HCLIM12. This is primarily the result of the larger number of grid points (due to higher grid resolution) in HCLIM3 in each altitude segment (mostly on the order of 10–30 times more grid points).

Fig. 11

Seasonal changes by LC (LC-CTRL) in daily maximum (top row) and minimum (bottom row) T2m as a function of altitude over the southern Scandes. Model data has been binned into 20 m altitude (vertical) segments starting at 200 m and ending at 1500 m. Each dot represents the mean value in each of these segments

The LC T2m responses in Fig. 11 show warming in all seasons and in all height intervals although the warming rates at different heights vary between seasons. The change patterns in RCP4.5 are similar to RCP8.5 but with smaller magnitudes. In DJF HCLIM12 has a larger warming than HCLIM3 throughout the vertical essentially compensating for the differences seen in CTRL (see Fig. S6). It can also be seen that EDW is apparent in both MAM and SON daily minimum T2m in both scenarios; in RCP8.5 the warming at 1500 m is around 1.5–2 $^{\circ }$C stronger compared to the lowest levels, corresponding to $\sim$20–40% larger warming at higher levels (Fig. 11f, h). The EDW magnitude is also larger in HCLIM12 than in HCLIM3, most notably in MAM. EDW is already seen in MC but the effect becomes stronger with time (not shown). The EDW response pattern is on the other hand not consistent throughout the seasons and time of day (maximum vs minimum T2m). For example, in JJA the warming is quasi-constant with height (Fig. 11c, g), while for DJF minimum T2m an EDW response is seen in the lower 800 m with nearly constant rate of warming above (Fig. 11e). For daily maximum T2m EDW of slightly lower magnitude is seen in SON while in MAM the relative warming becomes less for altitudes above around 700 m (Fig. 11 d and b respectively).

Fig. 12

DJF, MAM and SON changes by LC in; a solid Pr, b fraction of solid-to-total Pr, c snow covered area (snc) and d number of days with more than 30 cm snow depth (snd). The vertical binning of data has been described in Fig. 11

The EDW phenomena appears most clearly in SON, consistent with recent literature that has indicated a clear tendency of EDW (at least in model responses) in this season in northern hemisphere mid-latitude high-elevation regions (Palazzi et al. 2018). Palazzi et al. (2018) found two main factors behind the EDW in warming climate; a larger increase of long-wave down-welling radiation and a larger decrease of albedo, due to reduced snow cover, at higher elevations. The snow season is expected to shorten with rising temperatures, i.e. later onset in autumn and earlier termination in spring. The main consequence would be reduced albedo that may then exacerbate the warming through the resulting increase in absorption of incoming radiative energy. The snow-albedo effect will be most effective close to the average location of the snow line, i.e. where the average temperature is close to the melting point, which is at higher altitudes near the start and end of the snow season.

In line with this reasoning, Fig. 12 shows that the snow cover fraction in HCLIM12 and HCLIM3 decreases in LC (also in MC, not shown) and in SON the magnitude of the decrease becomes larger with altitude, in large part mirroring the reductions in the albedo (not shown). In MAM, the reduction of snow cover is also larger at higher altitudes, between 600–1200 m, while in DJF the largest reductions occur below ca 800 m.

The reduced snow cover is associated with decreases in snowfall rates (as well as other factors not analyzed in this study such as intermittent melting periods). In particular, in SON the decrease (in mm/d) becomes larger with height (Fig. 12a) while in MAM and DJF the change patterns are somewhat different with larger decreases in snowfall at lower altitudes and small changes at the highest elevations. In DJF both HCLIM12 and HCLIM3 even show increases at the highest altitudes. HCLIM3-GFDL stands out by having increases already from around 1000 m amounting to an increase of more than 2 mm/d near 1500 m altitude, corresponding to a near 30% increase. Earlier in the century, in MC with lower levels of warming, all models show a very distinct increase in DJF snowfall above $\sim$800 m in both RCP4.5 and RCP8.5 (not shown). The total (solid plus liquid) Pr over this region increases in LC in DJF, SON and MAM, with the largest increase in DJF by around 50% in GFDL runs and between 15% and 30% in EC-EARTH runs (not shown). The consequence, with regards to the mostly decreasing snowfall rates, is that the fraction of liquid compared to solid Pr increases on average (note the decreases in solid-to-total Pr ratio in Fig. 12b). As discussed in Räisänen (2021) near and long-term changes in the presence and amounts of snow in a warming climate involve competing effects of increased total Pr (leading to more snowfall where temperatures are cold enough) on the one hand and reduced snowfall fraction and higher frequency of surface melt episodes with warming on the other. The latter two factors tend to eventually dominate if temperatures continue rising (Räisänen 2021), in the colder far north or at higher elevations more prominently later in the century, as is clearly seen in the HCLIM simulations as well (Fig. 12).

The dependence on the emission scenario, and thus the level of temperature change, is also evident; the reduction in snowfall, snow cover and solid-to-total Pr fraction seen here is not as strong in RCP4.5 compared to RCP8.5. For example, the occurrence of days with at least 30 cm of snow depth (Fig 12d) is almost completely absent below ca 500 m by LC in RCP8.5 but still present in RCP4.5. At higher altitudes, between 800–1000m altitude (approximately the current location of the treeline), the number of days decreases in RCP8.5 by 30–60% in DJF and MAM. In SON, which includes the start of the snow season and therefore have few days with significant snow depth to start with, the corresponding number drops by around 90%. However, in RCP4.5 the reduction is mostly 20–40% points lower than in RCP8.5 (except for highest altitudes in DJF and MAM).

Fig. 13

Left: map of the Scandes and its orography (in meters, smoothed field from HCLIM3). Right: Percentage change (LC minus CTRL) in daily mean total (solid + liquid) precipitation (Tot. Pr; top panel) and solid precipitation (Solid Pr; bottom panel). For each step in the latitudinal direction the highest located grid point along the longitude axis in the smoothed orography is identified. The red line in the map shows this “ridge” of highest points, and is done for HCLIM12 and HCLIM3 separately. Averages are then calculated for points on either side of the ridge (“windward” and “leeward” respectively). The smoothening of the orography was done by calculating a rolling mean using a $48\times 48$ km two-dimensional window ($4\times 4$ and $16\times 16$ grid points for HCLIM12 and HCLIM3 respectively). Results are only shown for HCLIM12 and HCLIM3 forced by EC-EARTH and for the RCP8.5 scenario. Note the different scales on the y-axes in the line plots. Negative and positive values on the x-axis mean westward and eastward of the crest respectively

Overall, systematic or large differences between HCLIM12 and HCLIM3 in the snow climate are mostly identified between the respective GCM-HCLIM combinations rather than between HCLIM12 and HCLIM3 forced by the same GCM, meaning essentially that the HCLIM responses are governed to large extent by the forcing GCM or RCP scenario. Concerning snowfall, however, HCLIM3 has consistently larger amounts of snowfall compared to HCLIM12 in CTRL (not shown), especially at higher altitudes. Interestingly, the reduction of snowfall in the scenarios (except at highest altitudes in DJF) are on average around 5–10% lower in HCLIM3 compared to HCLIM12 for altitudes above 800 m (Fig. 12a), reflected in the smaller decreases in solid-to-total Pr fractions in HCLIM3 (Fig. 12b). The spatial patterns of these different model responses reveal that the smaller reduction in solid Pr in HCLIM3 is mainly limited to the mountain ridge and windward side (i.e. the west side due to predominantly westerly winds) of the mountains (Fig. 13). The shift from precipitation falling as snow to rain has been shown to cause a strengthening of rain shadows (increased drying ratio) (Pavelsky et al. 2012), and thus the smaller reduction in HCLIM3 on the western slopes can possibly mean a smaller increase in drying ratio. However, the reasons for the different responses in HCLIM12 and HCLIM3, and their impact on for example the drying ratio, are not entirely clear and are still under investigation. A major part of the the stronger reduction of the solid precipiation fraction is likely due to the enhanced warming over topography in HCLIM12 (of around 1 $^\circ$C in DJF and to a lesser extent also in MAM and SON, see Fig. 11), somewhat more pronounced on the western slopes.

Factors related to model physics may also influence the representation of snow (such as the partitioning of total precipitation into rain and snow, and snow depth and cover on the ground). Even though HCLIM12 and HCLIM3 use the same surface model they have for example different micro-physical schemes. An investigation of how and to what extent such factors influence the results presented here is however beyond the scope of this study. As a last note, the changes in the snow climate as discussed above are for the southern part of the Scandes (since this was the focus region for temperature change responses), however, similar but weaker response patterns are seen for the whole of the Scandes.

3.3.4 Urban temperature change

We further studied the change of the urban heat island (UHI) effect in the MC and LC periods compared to CTRL over four major cities in Fenno-Scandinavia; Copenhagen, Oslo, Stockholm and Helsinki. HCLIM3 include the Town Energy Balance model (TEB, Masson 2000) within the SURFEX land surface model. TEB allows more detailed representation of interactions between buildings and the environment, such as shadows, turbulence, heat conduction, water interception etc. To study the UHI effect, we defined urban and rural areas around each city based on the city size and the SURFEX tiles surrounding the city (see Figure S7 in Supplementary). The urban areas are between 200–700 km$^2$ (depending on city) within a box centered over each city, and the surrounding rural areas do not extend more than around 120 km away from the city area (Fig. S7). The urban and rural grids were selected from the urban and rural areas, respectively; the urban grid points are here defined as points where the town tile fraction is higher than 40%, whereas rural grid points are defined as points where the nature tile fraction exceeds 98%. The selected tile fraction thresholds are based on a compromise between having sufficient number of grid points (for urban areas) and having a clean separation of urban and rural areas. Further, to minimize the effects from the sea and inland water bodies, selected urban and rural grid points were removed if their inland water and sea tile fractions exceeded 2%. It should be noted that in HCLIM12 simulations all town tile fractions were set to rock fractions instead since no TEB model was used in HCLIM12.

Fig. 14

The urban heat island index (UHI) in HCLIM12 and HCLIM3 calculated for the RCP8.5 scenario over four major cities in Fenno-Scandinavia; Copenhagen, Oslo, Stockholm and Helsinki (see Fig. 2). The top row show absolute UHI values for CTRL (blue bars), MC (green bars) and LC (red bars) and the bottom row shows the future changes in UHI. H12 and H3 in x-axis labels stands for HCLIM12 and HCLIM3 respectively

SURFEX provides temperatures over different tiles in each grid cell. However, because the TEB scheme is deactivated in the HCLIM12 simulations, the temperature for town tile is unavailable. To provide a consistent comparison between HCLIM3 and HCLIM12, the urban and rural temperatures (T_urban and T_rural) are represented by grid average temperatures (of all tiles) of selected grid points respectively, and the UHI index is calculated by taking the difference, T_urban− T_rural. The calculations are performed for JJA during night (00–03 UTC) when the UHI effects is relatively large. There are 1840 values (92 values/year $\times$ 20 years) over each grid. Figure 14 shows that the UHI index is significantly larger (2–3 times larger) in HCLIM3 than in HCLIM12, the magnitude in HCLIM3 being in closer resemblance to observed rural-urban temperature gradients (Amorim et al. 2020). For MC and LC the UHI index decreases in the majority of cases, although the magnitude of the decreases are small (generally less than $-0.1\,^\circ$C). HCLIM3 shows consistently decreases in UHI index over all cities and time periods except for MC in Helsinki in HCLIM3-GFDL. In contrast, while HCLIM12 exhibits similar responses over Oslo, in the other urban regions the sign of change includes both negative and positive values. Lauwaet et al. (2016) studied future UHI changes over Brussels using a high-resolution urban climate model and found that UHI would slightly decrease in a warming climate. The reason was that in urban areas the increase in nighttime temperature was more effectively mixed in the lowest 400 m and thus the increase at the surface was quite small. In rural areas there was a strong inversion present (in the studied, pronounced, UHI events) that confined the excess warming near the surface, i.e. a larger warming, in essence causing a small decrease in overall UHI. Our UHI results for HCLIM3 are in accordance with Lauwaet et al. (2016), although it is not clear at this stage whether it is for the same reasons as described in their study. Keat et al. (2021) found similar distinct UHI responses over UK cities in a CPRCM compared to a coarser scale RCM. The CPRCM, with a better urban scheme, simulated the UHI phenomena in closer agreement with observations and also very small future changes in UHI, markedly lower than the strong amplification seen in the RCM.

4 Summary and conclusions

This study analyzes the simulated climate change over Fenno-Scandinavia in the HCLIM regional climate model applied at 3 and 12 km grid spacing. HCLIM was forced by EC-EARTH and GFDL-CM3 GCMs using two emission scenarios, RCP4.5 (EC-EARTH only) and RCP8.5. Apart from a 20 year historic period two future 20 year time slices were simulated; mid-century (2041–2060, “MC”) and end-of-century (2081–2100, “LC”). The simulated changes in seasonal large-scale circulation show significant differences between models in terms of temporal evolution (by mid- and late-century), magnitude and sign of change. Particularly in DJF and SON the GFDL GCM simulates very clear increase in the zonal flow as well as in synoptic activity (SA) over Fenno-Scandinavia, while EC-EARTH shows a smaller increase and even a decrease in SA. These changes are reflected in increased 10 m wind speed in GFDL simulations. In JJA both GCMs show reduced synoptic activity and weaker wind speed (especially in GFDL simulations) associated with a northward expanding Azores high.

The projections show warming over the region in all scenarios with progressively enhanced warming by mid- and end-of-century, by end-of-century ranging from around 2–3 °C in the RCP4.5 scenario to 4–7 °C in RCP8.5. The strongest warming occurs for daily minimum T2m during the cold season as expected from the large reduction in snow and ice. Another interesting aspect of the temperature changes is seen over the Scandes where the rate of warming is larger at elevated regions, a phenomena known as elevation dependent warming (EDW). EDW is most clearly visible in daily minimum T2m in MAM and SON with a 20–40% stronger warming at higher altitudes. The projected rising temperatures over Fenno-Scandinavia are further accompanied by moister and wetter conditions throughout the region, and the increase in near-surface specific humidity is overall consistent with the Clausius–Clapeyron (CC) relation ($\sim$7%/°C). Simultaneously, there is widespread increases in precipitation over the region, particularly in DJF and SON and consistent with the larger warming in GFDL the precipitation change is generally larger in GFDL than in EC-EARTH simulations. In JJA, though, average precipitation is suppressed in southern parts of Fenno-Scandinavia.

As expected, a more profound modulation of GCM model responses by HCLIM is seen for precipitation, and important differences also emerge between HCLIM12 and HCLIM3. With the much finer resolution in HCLIM compared to the GCMs, there is a general shift of the precipitation distribution in HCLIM towards higher intensities. One of the major societal challenges of climate change in Fenno-Scandinavia is the anticipated future increase in very intense precipitation events with warming. High percentiles (> 99th percentile) of daily precipitation are here shown to increase at a rate between 4-8% per degree warming with generally higher rates in JJA than in DJF. However, the most noteworthy response is for heavy precipitation on the hourly time scale in HCLIM12 and HCLIM3. Both models show similar increases for the highest percentiles in DJF, an indication that large-scale weather regimes largely influence precipitation distributions in this season and thus the difference in grid resolution and model physics between HCLIM12 and HCLIM3 plays a comparatively small role. In contrast, the heaviest hourly rainfall in JJA increase at a distinctly faster pace in HCLIM3 than in HCLIM12 irrespective of forcing GCM, at a rate that exceeds the CC relation. In HCLIM12 the rate of change tend to be on the order of CC.

Calculations of statistical significance showed that for changes in daily average precipitation the significance is generally smaller than for the maximum precipitation. In RCP4.5 the changes are overall less significant, with most often less than 50% of the domain having significant changes, irrespective of season. In RCP8.5 the degree of significant responses are in general larger, particularly in DJF, and also to a higher degree in GFDL than in EC-EARTH simulations due to the larger warming in GFDL. The significance also exhibits a clear sensitivity to the length of considered time period, systematically increasing from 5- to 20-year long periods and indicating that time-slice simulations should not be shorter than 20 years for proper estimation of changes in climate. Another consequence of the warming is a shift from precipitation falling as snow to rain. In the Scandes, the shift is seen at all altitudes, however, the overall increase in total precipitation over the Scandes leads to simulated increase in snowfall at higher altitudes (> $\sim$1000 m) in DJF (and partly in MAM), with the largest increase occurring in MC. Interestingly, the reduction in the fraction of solid precipitation is systematically less in HCLIM3 than in HCLIM12, largely confined to the western slopes, i.e. on the climatologically windward side of the mountains. The reasons for these different responses are not clear, calling for a more detailed analysis in a future study. Furthermore, the days with significant snow depth, here represented by 30 cm of snow, are diminishing rapidly in the scenarios, by around 25% in DJF and MAM in RCP4.5 LC at an altitude near the current treeline (around 800 m), the reduction being doubled in RCP8.5. Below 500 m days with significant snow depth occur very rarely in LC in RCP4.5 and becomes principally absent in RCP8.5.

To conclude, the GCMs overall exert a large control on the resulting responses of HCLIM whereby the respective GCM-HCLIM combinations simulate similar changes, at least for domain averages on seasonal time scales. However, for some variables and seasons the response in HCLIM3 deviates from that of HCLIM12 and the GCMs. It is most evident for precipitation and particularly in summer when a significant amount of precipitation originates from convective processes in the atmosphere which is better represented by HCLIM3. In particular, HCLIM3 projects distinctly larger increase in both daily and sub-daily summer precipitation, primarily for the highest intensities. In recent studies HCLIM3 has shown, similar as in other CPRCMs, superior skill in representing high-intensity precipitation in recent climate compared to coarser models (Médus et al. 2022; Belušić et al. 2020; Lind et al. 2020). Taken together, this provides higher confidence in the stronger future summer precipitation changes in HCLIM3 compared to HCLIM12 and the GCMs. Systematically different responses in HCLIM3 compared to HCLIM12 have been noted for other aspects as well—e.g. more realistic values of, and a consistent decrease in, the urban heat island (UHI) index over major cities during the summer season in Fenno-Scandinavia and the smaller reduction of solid precipitation in the Scandes. It is worth pointing out that the different urban climate response in HCLIM3 compared to HCLIM12 is most likely more related to the different treatment of the urban environment (the use of a urban model, TEB, in HCLIM3) rather than the higher grid resolution. Overall, these results indicate that HCLIM3 provides additional, and sometimes more reliable, information in scenarios of future climates over Fenno-Scandinavia. Dedicated studies of particular variables and processes, such as wind gusts and lightning associated with deep convection or rain-on-snow events, will help to further elucidate different, and perhaps improved, behavior of HCLIM3 in response to a changing climate. To more fully account for uncertainties related to future emissions of greenhouse gases and variability on annual and longer time scales requires ensembles of CPRCMs which still is very resource-intensive. Therefore, future work will explore additional approaches, for example event based downscaling, to be able to both address uncertainties due to natural variability while at the same time benefit from the added value in CPRCMs, clearly identified in this study.