Skip to main content
SpringerLink
Log in

A Note on the Inducibility of \(4\)-Vertex Graphs

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

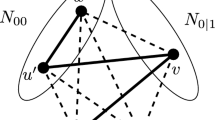
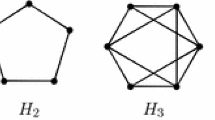
Abstract

There is much recent interest in understanding the density at which constant size graphs can appear in a very large graph. Specifically, the inducibility of a graph \(H\) is its extremal density, as an induced subgraph of \(G\), where \(|G| \rightarrow \infty \). Already for \(4\)-vertex graphs many questions are still open. Thus, the inducibility of the \(4\)-path was addressed in a construction of Exoo (Ars Combin 22:5–10, 1986), but remains unknown. Refuting a conjecture of Erdős, Thomason (Combinatorica 17(1):125–134, 1997) constructed graphs with a small density of both \(4\)-cliques and \(4\)-anticliques. In this note, we merge these two approaches and construct better graphs for both problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bollobás, B., Egawa, Y., Harris, A., Jin, G.: The maximal number of induced \(r\)-partite subgraphs. Graphs Combin. 11(1), 1–19 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bollobás, B., Nara, C., Tachibana, S.: The maximal number of induced complete bipartite graphs. Discrete Math. 62(3), 271–275 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  3. Brown, J., Sidorenko, A.: The inducibility of complete bipartite graphs. J. Graph Theory 18(6), 629–645 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bubeck, S., Linial, N.: On the local profiles of trees. arXiv:1310.5396 (2013, arXiv preprint)

  5. Conlon, D.: On the Ramsey multiplicity of complete graphs. Combinatorica 32(2), 171–186 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  6. Deza, A., Franek, F., Liu, M.: On a conjecture of Erdős for multiplicities of cliques. J. Discrete Algorithms 17, 9–14 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Erdős, P.: On the number of complete subgraphs contained in certain graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl 7, 459–464 (1962)

  8. Erdős, P., Lovász, L., Spencer, J.: Strong independence of graphcopy functions. In: Graph Theory and Related Topics, pp. 165–172 (1979)

  9. Evans, R., Pulham, J., Sheehan, J.: On the number of complete subgraphs contained in certain graphs. J. Combin. Theory Ser. B 30(3), 364–371 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  10. Exoo, G.: Dense packings of induced subgraphs. Ars Combin. 22, 5–10 (1986)

    MathSciNet  MATH  Google Scholar 

  11. Falgas-Ravry, V., Vaughan, E.: Applications of the semi-definite method to the Turán density problem for 3-graphs. Combin. Probab. Comput. 22(01), 21–54 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  12. Franek, F.: On Erdős’s conjecture on multiplicities of complete subgraphs - lower upper bound for cliques of size 6. Combinatorica 22(3), 451–454 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Franek, F., Rödl, V.: 2-colorings of complete graphs with a small number of monochromatic \(K_4\) subgraphs. Discrete Math. 114(1), 199–203 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  14. Giraud, G.: Sur le probleme de Goodman pour les quadrangles et la majoration des nombres de Ramsey. J. Combin. Theory Ser. B 27(3), 237–253 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  15. Goldreich, O., Goldwasser, S., Ron, D.: Property testing and its connection to learning and approximation. J. ACM 45(4), 653–750 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  16. Goodman, A.: On sets of acquaintances and strangers at any party. American Mathematical Monthly, pp. 778–783 (1959)

  17. Hatami, H., Hirst, J., Norine, S.: The inducibility of blow-up graphs. arXiv:1108.5699 (2011, arXiv preprint)

  18. Hirst, J.: The inducibility of graphs on four vertices. J. Graph Theory 75(3), 231–243 (2013)

    Article  MathSciNet  Google Scholar 

  19. Huang, H., Linial, N., Naves, H., Peled, Y., Sudakov, B.: On the densities of cliques and independent sets in graphs. arXiv:1211.4532 (2012, arXiv preprint)

  20. Huang, H., Linial, N., Naves, H., Peled, Y., Sudakov, B.: On the 3-local profiles of graphs. J. Graph Theory 76(3), 236–248 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Jagger, C., Šťovíček, P., Thomason, A.: Multiplicities of subgraphs. Combinatorica 16(1), 123–141 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  22. Linial, N., Morgenstern, A.: Graphs with few 3-cliques and 3-anticliques are 3-universal. J. Graph Theory (2014). doi:10.1002/jgt.21801

  23. Linial, N., Morgenstern, A.: On the number of 4-cycles in a tournament. arXiv:1405.1576 (2014, arXiv preprint)

  24. Lovász, L.: Large Networks and Graph Limits. American Mathematical Society, Providence (2012)

  25. Nieß, S.: Counting monochromatic copies of \(K_4\): a new lower bound for the Ramsey multiplicity problem. arXiv:1207.4714 (2012, arXiv preprint)

  26. Pippenger, N., Golumbic, M.: The inducibility of graphs. J. Combin. Theory Ser. B 19(3), 189–203 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  27. Razborov, A.: Flag algebras. J. Symbol. Logic 72(4), 1239–1282 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  28. Razborov, A.: Flag algebras: an interim report. Math. Paul Erdős II, 207–232 (2013)

  29. Shen, S.: On the parallelization of a search for counterexamples to a conjecture of Erdős. McMaster University Library (2012)

  30. Širáň, J.: A new lower bound for the inducibility of a graph. Math. Slovaca 34(4), 365–370 (1984)

    MathSciNet  MATH  Google Scholar 

  31. Sperfeld, K.: On the minimal monochromatic \(K_4\)-density. arXiv:1106.1030 (2011, arXiv preprint)

  32. Thomason, A.: A disproof of a conjecture of Erdős in ramsey theory. J. Lond. Math. Soc. 2(2), 246–255 (1989)

    Article  MathSciNet  Google Scholar 

  33. Thomason, A.: Graph products and monochromatic multiplicities. Combinatorica 17(1), 125–134 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  34. Vaughan, E.: Flagmatic: a tool for researchers in extremal graph theory (version 2.0) (2013). http://flagmatic.org/graph.html

  35. Wilf, H.S.: The patterns of permutations. Discrete Math. 257(2), 575–583 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  36. Wolf, J.: The minimum number of monochromatic 4-term progressions in \(\mathbb{Z}_p\). J. Combin. 1(1), 53–68 (2010)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Hebrew University, 91904 , Jerusalem, Israel

    Chaim Even-Zohar

  2. Department of Computer Science, Hebrew University, 91904 , Jerusalem, Israel

    Nati Linial

Authors
  1. Chaim Even-Zohar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nati Linial
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chaim Even-Zohar.

Additional information

Supported by grants from the ERC and from the ISF.

Appendix: The Inducibility of 5-Vertex Graphs

Appendix: The Inducibility of 5-Vertex Graphs

Table 2 Inducibilities of graphs on 5 vertices
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Even-Zohar, C., Linial, N. A Note on the Inducibility of \(4\)-Vertex Graphs. Graphs and Combinatorics 31, 1367–1380 (2015). https://doi.org/10.1007/s00373-014-1475-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-014-1475-4

Keywords

Search

Navigation