Abstract
We use a model of impressionable voters to study multi-candidate elections under different electoral rules. Instead of maximizing expected utility, voters cast their ballots based on impressions. We show that, under each rule, there is a monotone relationship between voter preferences and vote measures. The nature of this relationship, however, varies by electoral rule. Vote measures are biased upwards for socially preferred candidates under plurality rule, but biased downwards under negative plurality. There is no such bias under approval voting or Borda count. Voters always elect the socially preferred candidate in two-way races for any electoral rule. In multi-candidate elections, however, the ability to elect a Condorcet winner varies by rule. The results show that multi-candidate elections can perform well even if voters follow simple behavioral rules. The relative performance of specific electoral institutions, however, depends on the assumed behavioral model of voting.
Similar content being viewed by others
Notes
The nature of the ballot depends on the electoral rule. It corresponds to a “vote” under plurality rule, or in run-off elections, an “approval” under approval voting, a “negative vote” under negative plurality, and a ranking over candidates under the Borda rule.
Recent research (e.g., Spenkuch 2018) has argued that real electorates are best understood as heterogeneous, where some voters are rational, others impressionable or sincere. Modeling such electorates is valuable but very challenging. It also goes beyond the purpose of our paper.
The two remaining rules, Borda and runoff, are discussed later in Sect. 6.
Casting a “favorable ballot for candidate i” corresponds to voting for i under plurality rule, approving of i under approval voting, or not voting in opposition to i under negative plurality.
The propensity to abstain \(p_{\theta }^{t}(A)\) can be computed from the vote propensities \(p_{\theta }^{t}\) and so does not need to be tracked explicitly. We will show how to compute \(p_{\theta }^{t}(A)\) from \(p_{\theta }^{t}\) when we analyse the stationary distributions.
This disadvantage is present only under approval voting. To see this, suppose that, under approval voting, there are three candidates and only one type of voters. Consider the following two distributions over the set B: (1) a distribution where ballots (1, 1, 0) and (0, 1, 1) each have probability \(\frac{1}{2}\) of being cast; (2) a distribution where ballots (1, 1, 1) and (0, 1, 0) each have probability \(\frac{1}{2}\) of being cast. Both of these distributions yield vote propensities \((p(1),p(2),p(3))=(\frac{ 1}{2},1,\frac{1}{2})\), i.e., an outcome where candidate 2 gets a measure of 1 of approval votes, while candidates 1 and 3 get a measure of \(\frac{1}{2}\). If we were to work directly with the probability distribution \(\{r_{\theta }^{t}(b)\}_{b\in B}\), we would be able to differentiate between the two cases, while the distribution of vote propensities \(\{p_{\theta }^{t}(i)\}_{i\in N}\) is not able to do so.
Alternatively, we could consider a more complex updating rule where updating varies with the magnitude of the voter’s impressions. That is, a voter with a “very negative” impression of a candidate may decrease that candidate’s propensity more heavily compared to the case of “moderately negative” impressions, etc. Adding such complexity, however, does not change the qualitative results of the analysis.
As under plurality rule, we could allow an updating process where the increase or decrease of propensities depends also on the magnitude of impressions. But again, this will not change the qualitative results.
It is easy to see that if \(v_{\theta }^{i}>v_{\theta }^{j}\), then \(q_{\theta }(i)>q_{\theta }(j)\), \(E[\frac{1}{1+I_{\theta }(-i)}]>E[\frac{1}{1+I_{\theta }(-j)}]\) and \(E[\frac{1}{1+J_{\theta }(-i)}]<E[\frac{1}{1+J_{\theta }(-j)}]\), and therefore \(S_{\theta }(i)>S_{\theta }(j)\) under each rule.
Similar implications hold when comparing differences in vote measures across groups. Under plurality rule, controlling for the differences \(q_{\theta }(i)-q_{\theta }(j)\) between two groups, the difference in vote measures \(S_{\theta }(i)-S_{\theta }(j)\) will be larger for the group for which, on average, the number of candidates, excluding candidates i and j, that voters of that group like is lower. Under negative plurality, in contrast, the difference in vote measures \(S_{\theta }(i)-S_{\theta }(j)\) will be larger for the group for which, on average, the number of candidates, other than i and j, that voters of that group like is larger.
A Condorcet winner beats all other candidates in pair-wise comparison. A Condorcet loser is beaten by all other candidates in pair-wise competition.
See Andonie and Diermeier (2019) for the details under plurality rule. The same holds for the other rules.
Two-candidate elections under plurality rule with impressionable voters have been analysed in detail in Andonie and Diermeier (2019). Here, we focus on the comparison among the three rules. We omit the proof of Proposition 3. The proof follows immediately by noting that the difference in the measures of votes of the two candidates, by Proposition 2, is \(S(1)-S(2)=\sum _{\theta }s_{\theta }(q_{\theta }(1)-q_{\theta }(2))\) in all three rules, and then using the same argument as in plurality rule.
Under approval voting, a voter that decides to vote will never vote for (or approve) both candidates, therefore (1, 1) can be eliminated from the set \(B^{a}\). In the negative rule, choosing action (1, 1) (i.e., abstention) is the same as choosing action (0, 0) in the other rules. Therefore, all sets B are the same in the three rules, and so their equilibria and associated behavior of voters will also be the same.
Under plurality rule, in the rational voter model there may be equilibria where voters vote for two of the candidates that excludes the uniformly preferred candidate. See, e.g., Proposition 1 in Myerson (2002).
Under negative plurality, in the rational voter model there may be equilibria where all candidates have a positive probability of winning. See, e.g., Proposition 2 in Myerson (2002).
The assumptions that the measures of groups 1 and 2 of voters are the same, and that the component of impressions voters of groups 1 and 2 associate with candidate 3, i.e., parameter v, is the same for the two groups, are made for simplicity. The ordering of the three rules characterized in Lemma 1 does not change if, e.g., the parameters v of the two groups differ, but are close to one another.
Other cases that may be interesting are as follows. (1) If \(v>1\) and \(w>0\) then candidate 3 is “ranked” first by all voters. The analysis of this case is similar to that of \(v>1\) from the previous section, with similar conclusions. (2) If \(v<0\) and \(w<0\) then candidate 3 is “ranked” last by all voters. Again, the analysis of this case is similar to that of \(v<0\) from the previous section. (3) If \(v>1\) and \(w<0\) then voters of groups 1 and 2 “rank” candidate 3 first, while voters of group 3 “rank” candidate 3 last. The analysis and insights are similar to the case we discuss in this section.
The threshold \(w^{\phi }\) depends on various parameters such as v, F(.), \(\alpha\), etc. To simplify notation, we will write \(w^{\phi }\). It is possible that a value of w with this property does not exist. For example, if \(s\in (\frac{1}{4},\frac{1}{3})\), then in the plurality rule, a \(w^{p}\) with this property exists for any \(v<0\); in the approval rule, a \(w^{a}\) exists only for v with \(v^{a}<v<0\); while in the negative rule, a \(w^{n}\) exists only for v with \(v^{n}<v<0\). Moreover, the two cutoffs of v for the existence in the approval and negative rules are such that \(v^{a}<v^{n}<0\).
Specifically, the probabilities of positive impression of candidate 2 are such that: \(q_{1}(2),q_{2}(2)>\frac{1}{2}\) and \(q_{3}(2)<\frac{1}{2}\). This follows because v is large (in absolute value), and therefore the probabilities of positive impression of candidate 2 for groups 1, and 2 are: \(q_{1}(2),q_{2}(2)>\frac{1}{2}\). At the same time, the corresponding probability for group 3 is \(q_{3}(2)<\frac{1}{2}\) because group 3 of voters rank candidate 2 last.
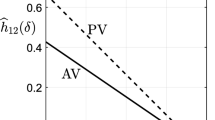
Indeed, Lemma 1 implies that, if, for a given set of values of the model’s parameters (e.g., fixed components v, or w, distribution F(.), weight \(\alpha\), etc.), candidate 3 wins under negative plurality, or approval voting, then he must also win under plurality rule. However, this allows the possibility that candidate 3 wins under plurality rule, but loses under negative plurality, or approval voting, for some values of the parameters that fall under the case considered. In other words, the set of parameters’ values under which candidate 3 wins is largest under plurality rule, followed by approval voting, and is smallest under negative plurality.
In the election considered by Myerson and Weber (1993), the utilities (which correspond to the vectors of fixed components in the impressionable voter model) of the three groups of voters are: \(u_{1}=\{10,9,0\}\), \(u_{2}=\{9,10,0\}\) and \(u_{3}=\{0,0,10\}\). As the differences over candidates 1 and 2 of voters in groups 1 and 2 are small relative to their strong opposition of candidate 3, we consider the division between groups 1 and 2 to be “small”.
If \(\alpha \rightarrow 0\), then it can be shown that \(S(1)-S(3)\rightarrow -0.1\) under plurality rule, and \(S(1)-S(3)\rightarrow 0.2\) under approval voting. On the other hand, if \(\alpha \rightarrow +\infty\) then \(S(1)-S(3)\) converges to zero, from above, under both plurality and approval rules. Therefore, if the distribution function F() is continuous, then, e.g., if \(\alpha\) is sufficiently small, then \(S(1)-S(3)<0\) under plurality rule, and \(S(1)-S(3)>0\) under approval voting.
In a recent paper, Bouton and Ogden (2021) consider a model of ethical voting under plurality, and runoff rules, and find that the set of equilibria of their model depends on the magnitude of voters’ preferences as well. We discuss the runoff rule in the next section.
The analysis can be obtained from the authors upon request.
The most common threshold is \(h=0.5\), but other thresholds are also used, typically below 0.5 (Bouton 2013).
If \(n=2\) then there is no difference between the runoff and plurality rule.
We are assuming that the socially preferred candidate wins when confronting a less preferred candidate in the second round. However, under some particular cases this may not hold, e.g., a Condorcet winner can lose to a less preferred candidate in the second round, if the preferences of voters preferring the Condorcet winner are substantially “weaker” than those of voters preferring the opponent candidate (this can be seen by writing the difference of measures of votes in the second round, \(S^{II}(1)-S^{II}(2)\) from above, in terms of the distribution function F(.), and impression components \(v_{\theta }^{1}\) and \(v_{\theta }^{2}\).).
We note that differences in impression probabilities \(q_{\theta }(1)-q_{\theta }(i)\) also influence the sign of \(S^{I}(1)-S^{I}(i)\). However, they are relevant only when the differences in impression components \(v_{\theta }^{1}-v_{\theta }^{i}\) differ substantially across types of voters, and the socially preferred candidate corresponds to the Condorcet winner. In all other cases e.g., when the differences in impression components \(v_{\theta }^{1}-v_{\theta }^{i}\) are the same magnitude across types, or the socially preferred candidate corresponds to the utilitarian welfare maximizing candidate, the influence of the differences \(q_{\theta }(1)-q_{\theta }(i)\) is irrelevant.
To break the tie between candidates 2 and 3, we can assume, for example, that voters of group 2 marginally prefer candidate 2 to candidate 3, i.e., their vector of fixed components is \(u_{2}=\{0,1+\eta ,1\}\), where \(\eta >0\) and small. The qualitative results of Proposition 6 will be the same.
They also apply to the election with four candidates, and three groups of voters we discuss below.
For voters of group 1: \(v_{1}^{3}=0\) and \(a_{1}=\frac{1}{3}\), while for voters of group 2: \(v_{2}^{3}=1\) and \(a_{2}=\frac{2}{3}\).
As in the previous example, to break the tie between candidates 3 and 4, we can assume, for example, that a majority of voters marginally prefers candidate 3 to candidate 4. Again, the qualitative results will be the same as in Proposition 7.
For some common distributions, e.g., \(U[-1,+1]\), \(\alpha ^{*}=+\infty\). So they do not require restrictions on the values of \(\alpha\).
For voters of group 1: \(v_{1}^{2}=0\), \(v_{1}^{4}=0\) and \(a_{1}=\frac{1}{4}\), while for voters of group 3: \(v_{3}^{2}=0\), \(v_{3}^{4}=1\) and \(a_{3}=\frac{1 }{2}\).
For voters of group 2 we have that \(q_{3}(1)=q_{3}(3)\), and therefore their votes do not influence the difference \(S^{I}(1)-S^{I}(3)\).
We discuss laboratory experiments in the Conclusion. Here we focus on multi-candidate elections. The absence of studies of two candidate elections under different electoral rules may be due to the fact that in a rational voter model all voting rules lead to equivalent outcomes.
See Andonie and Diermeier (2017) for details.
In the run-off elections we studied previously only two candidates can run in the second round. However, it is straightforward to modify the model and its analysis so that three candidates can run in the second round, like in the French elections.
References
Achen CH, Bartels LM (2002) Blind Retrospection: Electoral Responses to Droughts, Flu, and Shark Attacks. In: Presented at the Annual Meeting of the APSA, Boston, September, 2002
Achen CH, Bartels LM (2004) Musical Chairs: Pocketbook Voting and the Limits of Democratic Accountability. In: Presented at the Annual Meeting of the APSA, Chicago, September, 2004
Achen CH, Bartels LM (2016) Democracy for Realists: Why Elections Do Not Produce Responsive Government. and Princeton, NJ: Princeton University Press
Andonie C, Diermeier D (2017) Path-Dependency and Coordination in Multi-Candidate Elections with Behavioral Voters. J Theor Polit 29(4):520–545
Andonie C, Diermeier D (2019) Impressionable voters. Am Econ J Microecon 11(1):79–104
Ashworth S (2012) Electoral accountability: recent theoretical and empirical work. Annu Rev Polit Sci 15:183–201
Ashworth S, Bueno E, de Mesquita (2014) Is Voter Competence Good for Voters?: Information, Rationality, and Democratic Performance. Am Polit Sci Rev 108(3):565–587
Bendor J (2010) Bounded Rationality and Politics. Berkeley and Los Angeles: University of California Press
Bendor J, Diermeier D, Ting M (2003) A behavioral model of turnout. Am Polit Sci Rev 97:261–280
Bendor J, Kumar S, Siegel DA (2010) Adaptively rational retrospective voting. J Theor Polit 22(1):26–63
Bendor J, Diermeier D, Siegel D, Ting M (2011) A Behavioral Theory of Elections. Princeton University Press, Princeton
Bordignon M, Nannicini T, Tabellini G (2016) Moderating political extremism: single round versus runoff elections under plurality rule. Am Econ Rev 106(8):2349–2370
Borgers T, Sarin R (2000) Naive reinforcement learning with endogenous aspirations. Int Econ Rev 41:921–950
Bouton L (2013) A theory of strategic voting in runoff elections. Am Econ Rev 103:1248–1288
Bouton L, Castanheira M (2012) One person, many votes: divided majority and information aggregation. Econometrica 80(1):43–87
Bouton L, Gratton G (2015) Majority runoff elections: Strategic voting and Duverger’s hypothesis. Theor Econ 10:283–314
Bouton L, Castanheira M, Llorente-Saguer A (2016) Divided majority and information aggregation: theory and experiment. J Public Econ 134:114–128
Bouton L, Castanheira M, Llorente-Saguer A (2017) Multicandidate elections: aggregate uncertainty in the laboratory. Games Econom Behav 101:132–150
Bouton L, Ogden BG (2021) Group-based voting in multicandidate elections. J Politics 83(2):468–482
Brams S, Fishburn P (2005) Going from theory to practice: the mixed success of approval voting. Soc Choice Welf 25:457–74
Brams S, Nagel J (1991) Approval voting in practice. Public Choice 71(1/2):1–17
Bush R, Mosteller F (1955) Stochastic Models of Learning. Wiley, New York
Cho I-K, Matsui A (2005) Learning aspiration in repeated games. J Econ Theory 124:171–2001
Cole S, Healy A, Werker E (2012) Do voters demand responsive governments? evidence from Indian disaster relief. J Dev Econ 97:167–181
Cox Gary W (1997) Making Votes Count. Cambridge University Press, Cambridge
Cox GW (1994) Strategic voting equilibria under the single non-transferable vote. Am Polit Sci Rev 88:608–621
Diermeier D, Krehbiel K (2003) Institutionalism as a Methodology. J Theor Polit 15(2):123–144
Diermeier D, Li C (2017) Electoral control with behavioral voters. J Polit 79(3):890–902
Fey M (1997) Stability and coordination in Duverger’s law: a formal model of pre-election polls and strategic voting. Am Polit Sci Rev 91:135–147
Fishburn P, Little J (1988) An experiment in approval voting. Manag Sci 34(5):555–68
Forsythe R, Myerson RB, Rietz TA, Weber RJ (1993) An experiment on coordination in multicandidate elections: the importance of polls and election histories. Soc Choice Welf 10:223–247
Forsythe R, Myerson R, Rietz T, Weber R (1996) An experimental study of voting rules and polls in three-candidate elections. Int J Game Theory 25:355–383
Fujiwara T (2011) A regression discontinuity test of strategic voting and Duverger’s law. Q J Polit Sci 6:197–233
Gasper JT, Reeves A (2011) Make it rain? retrospection and the attentive electorate in the context of natural disasters. Am J Polit Sci 55(2):340–355
Healy A, Mo C, Malhotra N (2010) Irrelevant events affect voters’ evaluations of Government performance. Proc Natl Acad Sci 107(28):12506–12511
Hilgard ER, Bower GH (1966) Theories of learning. Appleton-Century-Crofts, New York
Karandikar R, Mookherjee D, Ray D, Vega-Redondo F (1998) Evolving aspirations and cooperation. J Econ Theory 80:292–331
Kinder DR (1998) Opinion and Action in the Realm of Politics. In: The Handbook of Social Psychology, ed. D. Gilbert, S. Fiske and G. Lindzey. 4 ed. Boston: McGraw-Hill pp 778–867
Krishna V, Morgan J (2015) Majority Rule and Utilitarian Welfare. Am Econ J Microecon 7(4):339–75
Levine DK, Palfrey TR (2007) The Paradox of voter participation? A Laboratory study. Am Polit Sci Rev 101(1):143–158
Myatt DP, Fisher SD (2002a) Everything is Uncertain and Uncertainty is Everything: Strategic Voting in Simple Plurality Elections. University of Oxford, Discussion Paper Series, Number 115
Myatt DP (2007) On the theory of strategic voting. Rev Econ Stud 74:255–281
Myatt DP, Fisher SD (2002) Tactical coordination in plurality electoral systems. Oxford Rev Econ Policy 18(4):504–522
Myerson RB (1999) Theoretical comparisons of electoral systems. Eur Econ Rev 43:671–697
Myerson RB (2002) Comparison of Scoring Rules in Poisson Voting Games. J Econ Theory 103:219–251
Myerson RB, Weber RJ (1993) A theory of voting equilibria. Am Polit Sci Rev 87:102–114
Nunez M (2014) The strategic sincerity of approval voting. Econ Theor 56:157–189
Palfrey TR (1989) A mathematical proof of Duverger’s Law. In: Peter CO (ed) Models of strategic choice in politics. University of Michigan Press, pp 69–92
Palfrey T, Rosenthal H (1983) A strategic calculus of voting. Public Choice 41:7–53
Palfrey T, Rosenthal H (1985) Voter participation and strategic uncertainty. Am Polit Sci Rev 79:62–78
Palomino F, Vega-Redondo F (1999) Convergence of Aspirations and (partial) Cooperation in the Prisoner’s Dilemma. Int J Game Theory 28:465–488
Pons V, Tricaud C (2018) Expressive voting and its cost: evidence from runoffs with two or three candidates. Econometrica 86(5):1621–1649
Richard C, James M (1963) A Behavioral Theory of the Firm. Prentice Hall, Englewood Cliffs
Schuessler AA (2000) Expressive voting. Ration Soc 12(1):87–119
Simon H (1955) A behavioral model of rational choice. Q J Econ 69(1):99–118
Spenkuch JL (2018) Expressive vs. strategic voters: an empirical assessment. J Public Econ 165:73–81
Thorndike EL (1898) Animal intelligence: an experimental study of the associative processes in animals. Psychol Rev (Monograph Supplement) 2(8)
Wolfers J (2002) Are Voters Rational? Evidence from Gubernatorial Elections. Stanford GSB Working Paper no. 1730
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Proposition 1
The proof for the characterization of the stationary distributions under approval voting, and negative plurality is similar to that under plurality rule (Andonie and Diermeier 2019, Lemma 1). First, consider approval voting. The equation for the updating of propensity \(p_{\theta }^{t}(i)\) for candidate \(i\in N\) can be written concisely as
This implies
In a stationary distribution, the distributions of propensities \(p_{\theta }^{t}\) and aspirations \(a_{\theta }^{t}\) do not depend on time t, and therefore, dropping the index t in the previous equation, we obtain
Because there is a continuum of voters of type \(\theta\), this implies that the measure of voters of type \(\theta\) that vote for (or, approve) candidate i is: \(S_{\theta }(i)=E[p_{\theta }(i)]=q_{\theta }(i)\).
In regard to abstentions, the equation for the updating of abstention propensity \(p_{\theta }(A)\) is: \(p_{\theta }^{t+1}(A)=(1-\lambda _{p})p_{\theta }^{t}(A)+\lambda _{p}{\mathbf {1}}_{\{I_{\theta }^{t}=0\}}\). Following the same steps as above, we obtain in a stationary distribution \(S_{\theta }(A)=\prod _{j\in N}(1-q_{\theta }(j))\).
Now, consider negative plurality. The equation for the updating of propensity \(p_{\theta }^{t}(i)\) for a candidate \(i\in N\) can be written concisely as
This implies
Similarly, as above, in a stationary distribution we obtain
In a stationary distribution, aspirations \(a_{\theta }\) are non-random and are equal to \(a_{\theta }=\sum _{j\in N}\frac{v_{\theta }^{j}}{n}\). This permits us to drop the conditional event \(\pi _{\theta }(i)<a_{\theta }\) in the expectation term above (see also Andonie and Diermeier 2019, Proof of Lemma 1), and therefore to obtain
Finally, the equation for updating the abstention propensity \(p_{\theta }^t(A)\), under negative plurality, is: \(p_{\theta }^{t+1}(A)=(1-\lambda _p)p_{\theta }^{t}(A)+\lambda _p{\mathbf {1}}_{\{J_{\theta }^t=0\}}\). Taking expectation in this equation and, dropping the time index t, we obtain that in a stationary distribution the measure of voters of type \(\theta\) that abstain is: \(S_{\theta }(A)=\prod _{j\in N}q_{\theta }(j)\).
1.2 Proof of Proposition 2
In the plurality rule, by Proposition 1, the measure of votes candidate i obtains in a stationary distribution is \(S_{\theta }(i)=q_{\theta }(i)E[ \frac{1}{1+I_{\theta }(-i)}]\). Since the expectation term can be decomposed as
it follows that we can write \(S_{\theta }(i)\) as:
Therefore the difference in measures of votes of candidates i and j is:
In the approval rule, by Proposition 1, the measure of votes candidate i obtains in a stationary distribution is \(S_{\theta }(i)=q_{\theta }(i)\). Therefore the difference in measures of votes of candidates i and j is:
In the negative plurality rule, by Proposition 1, the measure of votes candidate i obtains in a stationary distribution is: \(S_{\theta }(i)=1-(1-q_{\theta }(i))E[\frac{1}{n-I_{\theta }(-i)}]\). Since we can decompose the expectation term as
it follows that \(S_{\theta }(i)\) can be alternatively written:
Therefore, the difference between the measures of votes of candidates i and j is:
Now let us formally prove the observation on the differences between the three electoral rules discussed after Proposition 2. Consider first the plurality rule. We note that \(E[\frac{1}{1+I_{\theta }(-i,j)}]\) decreases with the probability of positive impression \(q_{\theta }(l)\), for each candidate \(l\ne i,j\). This can be seen by writing
Consider now two candidates i, j at the top of the vector of fixed components \(u_{\theta }\), and two candidates \(i^{\prime }\), \(j^{\prime }\) at the bottom of the vector \(u_{\theta }\). The probabilities of having a good impression of candidates i and j are larger than the corresponding probabilities of candidates \(i^{\prime }\) and \(j^{\prime }\): \(q_{\theta }(i),q_{\theta }(j)>q_{\theta }(i^{\prime }),q_{\theta }(j^{\prime })\). As the expectation \(E[\frac{1}{1+I_{\theta }(-i,j)}]\) decreases with \(q_{\theta }(l)\), for \(l\ne i,j\), this implies that \(E[\frac{1}{1+I_{\theta }(-i,j)} ]>E[\frac{1}{1+I_{\theta }(-i^{\prime },j^{\prime })}]\). In other words, if we control for the differences \(q_{\theta }(i)-q_{\theta }(j)\), the differences in measures of votes \(S_{\theta }(i)-S_{\theta }(j)\) are larger if candidates i and j are at the top of vector \(u_{\theta }\), and smaller if candidates i and j are at the bottom.
A similar reasoning applies to the negative plurality rule. In the negative plurality, the expectation term \(E[\frac{1}{n-1-I_{\theta }(-i,j)}]\) increases with the probability of positive impression \(q_{\theta }(l)\), for each candidate \(l\ne i,j\). To see this, we write:
Similarly as above, if we consider two candidates i and j at the top of the vector \(u_{\theta }\), and two candidates \(i^{\prime }\) and \(j^{\prime }\) at the bottom of the vector \(u_{\theta }\), we will have that \(q_{\theta }(i),q_{\theta }(j)>q_{\theta }(i^{\prime }),q_{\theta }(j^{\prime })\). But as the expectation \(E[\frac{1}{n-1-I_{\theta }(-i,j)}]\) increases with \(q_{\theta }(l)\), for \(l\ne i,j\), this implies that \(E[\frac{1}{ n-1-I_{\theta }(-i,j)}]<E[\frac{1}{n-1-I_{\theta }(-i^{\prime },j^{\prime })} ]\). Therefore, if we control for the differences \(q_{\theta }(i)-q_{\theta }(j)\), the differences in measures of votes \(S_{\theta }(i)-S_{\theta }(j)\) are smaller if candidates i and j are at the top of vector \(u_{\theta }\), and larger if candidates i and j are at the bottom.
1.3 Proof of Proposition 4
By Proposition 1, under each of the three electoral rules, the stochastic process has a unique stationary distribution. In the stationary distribution, the aspirations of the two groups of voters are: \(a_{1}=\frac{1+v}{3}\) and \(a_{2}=\frac{1+v}{3}\). Given these aspirations, we can compute the probabilities of positive impression for each of the three candidates, across the two groups, as follows:
Using Proposition 2, the difference between the measures of votes of candidates 1 and 3 in the plurality rule is
It is easy to verify that, as intuition suggests, the difference \(S(1)-S(3)\) decreases with v. When \(v=\frac{1}{2}\) we have: \(S(1)-S(3)=\frac{1}{2}(- \frac{1}{2}+F(\frac{3/2}{3\alpha }))^{2}>0\), while when \(v=1\) we have \(S(1)-S(3)=\frac{1}{2}(F(\frac{-1}{3\alpha })-F(\frac{2}{3\alpha }))(\frac{1}{ 2}+\frac{1}{2}F(\frac{-1}{3\alpha }))<0\). Therefore, there exists a cutoff \(v_{p}^{*}\) with \(v_{p}^{*}\in (\frac{1}{2},1)\) such that if \(v<v_{p}^{*}\) then \(S(1)-S(3)>0\), and if \(v>v_{p}^{*}\) then \(S(1)-S(3)<0\).
In the approval rule, we can use Proposition 2 to compute the difference between the measures of votes of candidates 1 and 3 as follows:
Again, it is easy to verify that the difference \(S(1)-S(3)\) decreases with v. When \(v=\frac{1}{2}\), we have \(S(1)-S(3)=0\). Therefore if \(v<v_{a}^{*}=\frac{1}{2}\) then \(S(1)-S(3)>0\), and if \(v>v_{a}^{*}= \frac{1}{2}\) then \(S(1)-S(3)<0\).
Finally, in the negative plurality rule, the difference in the vote measures of candidates 1 and 3, using Proposition 2, is
Again, as in the case of the other two rules, the difference \(S(1)-S(3)\) decreases with v. When \(v=\frac{1}{2}\) we have \(S(1)-S(3)=-\frac{1}{2}(- \frac{1}{2}+F(\frac{3/2}{3\alpha }))^{2}<0\), and when \(v=0\) we have \(S(1)-S(3)=\frac{1}{2}(F(\frac{1}{3\alpha })-F(\frac{-2}{3\alpha }))(1-\frac{1 }{2}F(\frac{1}{3\alpha }))>0\). Therefore, there exists a cutoff \(v_{n}^{*}\) with \(v_{n}^{*}\in (0,\frac{1}{2})\) such that if \(v<v_{n}^{*}\) then \(S(1)-S(3)>0\), and if \(v>v_{n}^{*}\) then \(S(1)-S(3)<0\).
1.4 Proof of Lemma 1
Under each of the three electoral rules, the stochastic process has a unique stationary distribution. In the stationary distribution, the aspirations of the three groups of voters are: \(a_{1}=\frac{1+v}{3}\), \(a_{2}=\frac{1+v}{3}\) and \(a_{3}=\frac{w}{3}\). Then, we can compute the probabilities of having a positive impression, for each group \(\theta =1,2,3\), and for each candidate \(i=1,2,3\) as follows:
Using Proposition 2, the difference between candidates 1’s and 3’s measures of votes under plurality rule is
therefore the cutoff \(w^{p}\) in the plurality rule is characterized by:
Similarly, for the approval rule, we can use Proposition 2 to compute the difference \(S(1)-S(3)\) as follows:
Therefore the cutoff \(w^{a}\) in the approval rule is characterized by:
Finally, for the negative plurality rule, using Proposition 2, the difference \(S(1)-S(3)\) is
and so the cutoff \(w^{n}\) is characterized by the equation
We first make a simple observation on the relationship between the value of v and the thresholds \(w^{p}\), \(w^{a}\), and \(w^{n}\). Intuitively, when v increases in absolute value, the relative support of voters in groups 1 and 2 for candidate 1 increases. Similarly, when w increases, the relative support of voters in group 3 for candidate 3 increases. As \(w^{p}\), \(w^{a}\), and \(w^{n}\) are defined as the threshold for w at which the relative support of groups 1 and 2 for candidate 1, and support of group 3 for candidate 3 are balanced, then all three thresholds \(w^{p}\), \(w^{a}\), and \(w^{n}\) should decrease with v. Indeed, it is easy to prove this result also formally, by observing that the left sides of the three equations characterizing \(w^{p}\), \(w^{a}\), and \(w^{n}\) all decrease with v, while the right sides all increase with w.
Let us next prove two preliminary results. In the first preliminary result, we show that for any \(v\le -1\) we have: \(w^{p}<w^{a}<w^{n}\). If \(v\le -1\), then, using the equation for \(w^{p}\), and because \(w^{p}\ge 0\), we can write:
Therefore \(w^{p}<w^{a}\). Similarly, using the equation for \(w^{n}\) we can write:
Therefore \(w^{a}<w^{n}\). Thus, when \(v\le -1\) we have \(w^{p}<w^{a}<w^{n}\).
In the second preliminary result, we will show that if \(v=0\) then: (a) If \(s< \frac{1}{3}\) then \(w^{p},w^{a},w^{n}<1\); and (b) If \(s>\frac{1}{3}\) then \(w^{p},w^{a},w^{n}>1\). When \(v=0\), the equation characterizing \(w^{p}\) in the plurality rule becomes
Therefore, if \(s>\frac{1}{3}\) we must have \(w^{p}>1\); and if \(s<\frac{1}{3}\) we must have \(w^{p}<1\). In the approval rule, when \(v=0\) the equation characterizing \(w^{a}\) is
Therefore, if \(s>\frac{1}{3}\) then we must have \(w^{a}>1\); and if \(s<\frac{1 }{3}\) then we must have \(w^{a}<1\). Finally, in the negative plurality rule, the equation characterizing the threshold \(w^{n}\) for \(v=0\) is
As in the other two rules, if \(s>\frac{1}{3}\) we must have \(w^{n}>1\); and if \(s<\frac{1}{3}\) we must have \(w^{n}<1\).
We can now use these two preliminary results to prove the lemma. Suppose first that \(s<\frac{1}{3}\). The first preliminary result from above shows that if \(v\le -1\) then \(w^{p}<w^{a}<w^{n}\). When \(v=0\), we can use the equation for \(w^{p}\) and the second preliminary result to write:
Therefore, if \(v=0\) then \(w^{a}<w^{p}\). Similarly, if \(v=0\) we can use the equation for \(w^{n}\) and the second preliminary result to write:
and so \(w^{n}<w^{a}\). Thus, if \(v=0\) then \(w^{n}<w^{a}<w^{p}\).
Because for all \(v\le -1\) we have \(w^{p}<w^{a}<w^{n}\), and for \(v=0\) we have \(w^{n}<w^{a}<w^{p}\), there must exist a cutoff \(v^{*}\in (-1,0)\) at which \(w^{p}=w^{a}=w^{*}\). We will show that at the cutoff \(v=v^{*}\) we also have \(w^{n}=w^{*}\). To see this, we write the equations for thresholds \(w^{p}\) and \(w^{a}\) when \(v=v^{*}\) as
and
Multiplying the second equation by \(\frac{3}{2}\) and then subtracting the two equations we obtain:
Therefore when \(v=v^{*}\) we also have \(w^{n}=w^{*}\). We will next show that if \(v<v^{*}\) then \(w^{p}<w^{a}<w^{n}\); while if \(v>v^{*}\) then \(w^{n}<w^{a}<w^{p}\). Consider the two equations characterizing the thresholds \(w^{p}\) and \(w^{a}\), and let us divide the two equations side by side:
It can be shown that the right hand side increases in v. This can be shown by differentiating the expression and proving that its derivative is positive. At the same time, \((\frac{1}{2}+\frac{1}{2}F(\frac{w^{p}}{3\alpha } ))\) decreases in v. Therefore, in order to preserve the balance of the right and left side of the equation, it must then be that the ratio \(\frac{F( \frac{w^{p}}{3\alpha })+F(\frac{2w^{p}}{3\alpha })-1}{F(\frac{w^{a}}{3\alpha })+F(\frac{2w^{a}}{3\alpha })-1}\) increases in v. When \(v=v^{*}\) we have \(w^{p}=w^{a}=w^{*}\), and so \(\frac{F(\frac{w^{p}}{3\alpha })+F( \frac{2w^{p}}{3\alpha })-1}{F(\frac{w^{a}}{3\alpha })+F(\frac{2w^{a}}{ 3\alpha })-1}=1\). This implies
Similarly, we can divide the equations characterizing the thresholds \(w^{n}\) and \(w^{a}\) to obtain
As above, it can be shown that the right hand side of the equation decreases in v. As the term \((1-\frac{1}{2}F(\frac{w^{n}}{3\alpha }))\) increases in v, in order to preserve the balance, it must be that the ratio: \(\frac{F( \frac{w^{n}}{3\alpha })+F(\frac{2w^{n}}{3\alpha })-1}{F(\frac{w^{a}}{3\alpha })+F(\frac{2w^{a}}{3\alpha })-1}\) decreases in v. When \(v=v^{*}\) we have \(w^{n}=w^{a}=w^{*}\), and so \(\frac{F(\frac{w^{n}}{3\alpha })+F( \frac{2w^{n}}{3\alpha })-1}{F(\frac{w^{a}}{3\alpha })+F(\frac{2w^{a}}{ 3\alpha })-1}=1\). This implies:
Finally, let us prove part (2) of the lemma, where \(s>\frac{1}{3}\). From the second preliminary result, we know that when \(v=0\), we have \(w^{p},w^{a},w^{n}>1\). As all three thresholds \(w^{p}\), \(w^{a}\), and \(w^{n}\) decrease with v, this implies that for all \(v\le 0\), we have \(w^{p},w^{a},w^{n}>1\). Using the equation for threshold \(w^{p}\), and because \(v\le 0\) and \(w^{p}>1\), we can write:
Therefore \(w^{p}<w^{a}\). Similarly, using the equation for threshold \(w^{n}\), and because \(v\le 0\) and \(w^{p}>1\), we can write:
Therefore \(w^{a}<w^{n}\). Thus, for all \(v\le 0\) we have \(w^{p}<w^{a}<w^{n}\).
1.5 Proof of Proposition 5
The proof is similar to that of Proposition 1. Using the equations for the updating of propensities, we can write:
In a stationary distribution, the distributions of propensities and aspirations, \(p_{\theta }^{t}\) and \(a_{\theta }^{t}\), do not depend on time. Therefore, dropping the superscript time index t, we obtain:
Computing the expression on the right hand side, we obtain:
Finally, the equation for the updating of the abstention propensity is: \(p_{\theta }^{t+1}(A)=(1-\lambda _p)p_{\theta }^t(A)+\lambda _p{\mathbf {1}} _{\{I_{\theta }^t=0\}}\). Similarly as in the other electoral rules, this implies that the measure of voters of type \(\theta\) that abstain is \(S_{\theta }(A)=\prod _{j\in N}(1-q_{\theta }(j))\).
1.6 Proof of Proposition 6
Consider first the first round. In the stationary distribution of the first round, the aspirations of the two groups of voters are \(a_{1}=\frac{1}{3}\), and \(a_{2}=\frac{2}{3}\). The probabilities of positive impressions for each candidate \(i=1,2,3\) across the two groups of voters are
Because \(q_{\theta }(2)=q_{\theta }(3)\) for each group \(\theta =1,2\), the difference in measures of votes of candidates 2 and 3 is \(S^{I}(2)-S^{I}(3)=0\). On the other hand, the difference in measures of votes of candidates 1 and 2 is:
Therefore \(S^{I}(1)-S^{I}(2)>0\) if \(s>s^{*}\), where \(s^{*}=\frac{2}{3 }(1-\frac{1}{2}F(\frac{1}{3\alpha }))\) with \(s^{*}<\frac{1}{2}\). We can further show that the share of votes candidate 1 obtains in the first round is below 50%: \(S^{I}(1)<0.5(S^{I}(1)+S^{I}(2)+S^{I}(3))\), or equivalently \(S^{I}(1)<S^{I}(2)+S^{I}(3)\). Using the characterization of measures of votes in the stationary distribution and upon re-arranging, the condition can be written as:
Letting \(a=F(\frac{1}{3\alpha })\) and \(b=F(\frac{2}{3\alpha })\), the condition can be written as:
or, upon re-arranging:
We note that the left hand side is linear in b. Given that \(1\ge b\ge a\ge \frac{1}{2}\), if the inequality holds at \(b=a\) and \(b=1\), then the inequality will hold for all \(b\ge a\). The fact that inequality holds for \(b=a\), and \(b=1\) can be shown by straightforward algebra.
Consider now the second round, where candidate 1 confronts candidate 2. The difference in measures of votes of candidates 1 and 2 in the second round is:
As \(s<\frac{1}{2}\), we have \(S^{II}(1)-S^{II}(2)<0\), i.e., candidate 2 wins.
1.7 Proof of Proposition 7
In the stationary distribution of the first round, the aspirations of the three groups of voters are \(a_{1}=\frac{1}{4}\), \(a_{2}=\frac{1}{4}\) and \(a_{3}=\frac{1}{2}\). The probabilities of positive impressions for each candidate \(i=1,2,3\) are:
Because of the symmetry between candidates 1 and 2, we have \(S^{I}(1)=S^{I}(2)\). Similarly, by the symmetry of candidates 3 and 4, we have \(S^{I}(3)=S^{I}(4)\). Using previous results, the difference in measures of votes of candidates 1 and 3 is:
The difference \(S^{I}(1)-S^{I}(3)\) increases with s. If \(s=\frac{1}{3}\), then the difference \(S^{I}(1)-S^{I}(3)\) is:
Therefore, if the expression on the right hand is positive, then there exists a cutoff \(s^{*}<\frac{1}{3}\) such that for all \(s\in (s^{*}, \frac{1}{3})\) we have \(S^{I}(1)-S^{I}(3)>0\).
If \(\epsilon \sim U[-1,+1]\), then it can be shown by straightforward algebra that \((S^{I}(1)-S^{I}(3))_{s=\frac{1}{3}}>0\) for all \(\alpha \ge 0\). If \(\epsilon \sim N(0,1)\), we can show by numerical analysis that \((S^{I}(1)-S^{I}(3))_{s=\frac{1}{3}}>0\) for all \(\alpha \ge 0\) as well. For other distributions F(.), a sufficient condition that ensures that \((S^{I}(1)-S^{I}(3))_{s=\frac{1}{3}}>0\) is that \(\alpha <\alpha ^{*}\), where the cutoff \(\alpha ^{*}\) is a function of the distribution F(). If \(\alpha \rightarrow 0\) then the difference \((S^{I}(1)-S^{I}(3))_{s=\frac{1 }{3}}\rightarrow \frac{1}{2}>0\), and therefore, by continuity, \((S^{I}(1)-S^{I}(3))_{s=\frac{1}{3}}>0\) if \(\alpha\) is not “too large”.
Rights and permissions
About this article
Cite this article
Andonie, C., Diermeier, D. Electoral Institutions with impressionable voters. Soc Choice Welf 59, 683–733 (2022). https://doi.org/10.1007/s00355-022-01406-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-022-01406-6