Polarization and inefficient information aggregation under strategic voting

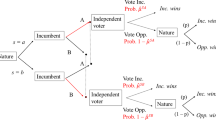
Abstract

We study a model of two-candidate electoral competition. In our model, each voter has single-peaked preferences for the consequences of policies, but voters receive only partial information about which policies cause their preferred consequences. If voters’ utility functions are convex, they prefer risk, which implies that a safe alternative may not be chosen even when this alternative results in the median voter’s preferred consequence with a probability of one. We provide a necessary and sufficient condition for the existence of a strategic voting equilibrium in which a risky policy that causes polarized consequences defeats the median voter’s preferred alternative. Even when the convexity of voters’ utility functions is weak, which means that policy polarization is socially undesirable, if voters are likely to receive insufficient information, the chosen policy is still polarized. In that case, social welfare is minimized. However, proposals by sufficiently well-informed candidates can eliminate the uncertainty of risky policies through a signaling effect, which, in turn, eliminates the perverse consequences.

Appendices

Appendix

A. Proofs

1.1 Proofs in Section 4

Proof of Lemma 1

If $x_{D}=x_{R}$, then, by Assumption 1, each candidate wins with probability 1/2. Therefore, we consider the case in which $x_{D}\ne x_{R}$. Without loss of generality, we assume that $x_{R}=1$ and $x_{D}=-1$.

As type $t=0$ voters are indifferent to which candidate is elected, such voters vote for the candidates with equal probability. Consider the other types. Let $\gamma = \frac{1-q}{q } \frac{\mathrm {Pr}(z _R= n\mathrel {|}\omega = -1)}{\mathrm {Pr}(z _R= n\mathrel {|}\omega = 1) }$ ($z_{R}$ be the number of voters who votes for R). Then, the best response of each voter of type $(t,\sigma )\in \{-1,1\}^{2}$ is as follows.

• 1. If $(t,\sigma )=(1,1)$, a voter votes for R if $\theta > \frac{ \gamma }{1+ \gamma }$.

• 2. If $(t,\sigma )=(1,-1)$, he votes for R if $\theta < \frac{1}{1+ \gamma }$.

• 3. If $(t,\sigma )=(-1,1)$, he votes for R if $\theta < \frac{\gamma }{1+ \gamma }$.

• 4. If $(t,\sigma )=(-1,-1)$, he votes for R if $\theta > \frac{ 1}{ 1+ \gamma }$.

Let $v_{R,\omega }(\gamma )$ be the probability with which a given voter votes for candidate R in state $\omega \in \{-1,1\}$ under $\gamma = \frac{1-q}{q } \frac{\mathrm {Pr}(z _R= n\mathrel {|}\omega = -1)}{\mathrm {Pr}(z _R= n\mathrel {|}\omega = 1) }$. Then,

$$\begin{aligned} v_{R,1}(\gamma )&=k_{1}\left[ \int _{ \max \left\{ \frac{ \gamma }{1+ \gamma },1/2\right\} }^1 \theta dF(\theta )+\int ^{ \min \left\{ 1,\frac{ 1}{1+ \gamma }\right\} }_{1/2}( 1-\theta ) dF(\theta )\right] \\&\quad +k_{-1}\left[ \int ^{\min \left\{ 1, \frac{ \gamma }{1+ \gamma }\right\} }_{1/2} \theta dF(\theta )+\int _{ \max \left\{ \frac{ 1}{1+ \gamma },1/2\right\} }^1 (1-\theta ) dF(\theta ) \right] +\frac{1-k}{2}\\ v_{R,-1}(\gamma )&=k_{1}\left[ \int _{ \max \left\{ \frac{ \gamma }{1+ \gamma },1/2\right\} }^1(1- \theta ) dF(\theta )+\int ^{ \min \left\{ 1,\frac{ 1}{1+ \gamma }\right\} }_{1/2}\theta dF(\theta )\right] \\&\quad +k_{-1}\left[ \int ^{\min \left\{ 1, \frac{ \gamma }{1+ \gamma }\right\} }_{1/2} (1-\theta ) dF(\theta )+\int _{\max \left\{ \frac{ 1}{1+ \gamma },1/2\right\} }^1 \theta dF(\theta ) \right] +\frac{1-k}{2}. \end{aligned}$$

From these equations, we obtain $v_{R,1}(\gamma )=1-v_{R,-1}(\gamma )\geqslant 1/2$ for each $\gamma$ (equality holds if $k_{1}=k_{-1}$). Then, $\gamma =(1-q)/q$, which characterizes the BNEs. Given this result, we know that in each BNE, a given voter votes for R with a probability that is greater than or equal to 1/2 (equality also holds if $k_{1}=k_{-1}$) in state $\omega =1$ and with the complement probability in state $\omega =-1$. Thus, each candidate wins with a probability that is greater than or equal to 1/2 in state $\omega =1$, and with the complement probability in state $-1$. $\square$

Proof of Lemma 3

Note that, by the definition of $\gamma$, the equilibrium condition is

$$\begin{aligned} \gamma =\varphi (\gamma ){:}{=}\frac{1-q}{q } \frac{\mathrm {Pr}(z _R= n\mathrel {|}\omega = -1)}{\mathrm {Pr}(z _R= n\mathrel {|}\omega = 1) }= \frac{1-q}{q}\left[ \frac{v_{R,-1}(\gamma )(1-v_{R,-1}(\gamma ))}{v_{R,1}(\gamma )(1-v_{R,1}(\gamma ))}\right] ^n. \end{aligned}$$

(4)

Therefore, a fixed point of $\varphi$ characterizes a BNE. Existence is guaranteed for the following reason. Note that $\sup _{\omega , \gamma } v_{R,\omega }(\gamma )<1$, and note that because the density of F has full support on (1/2, 1), $\inf _{\omega , \gamma } v_{R,\omega }(\gamma )>0$. Therefore, $0<\inf \varphi (\gamma )<\sup \varphi (\gamma )<\infty$. By the continuity of $\varphi$ and the intermediate value theorem, $\varphi$ has a fixed point. $\square$

Proof of Lemma 4

We first show the monotonicity of $v_{R,1}(\gamma )-v_{R,-1}(\gamma )$ if $\gamma \in (1/y,y)$.

Claim 1

$v_{R,1}(\gamma )-v_{R,-1}(\gamma )$ is increasing in $\gamma \in (1/y,y)$.

Proof

If $\gamma \in (1/y,y)$, the difference $v_{R,1}(\gamma )-v_{R,-1}(\gamma )$ is

$$\begin{aligned}&k_{1}\left[ \int _{1/2}^1 (1-2\theta ) dF(\theta )+ \int ^{ \min \left\{ 1,\frac{\gamma y}{1+ \gamma y}\right\} } _{1/2}(2\theta -1) dF(\theta )\right] \\&\quad + k_{-1}\left[ \int ^{\min \left\{ 1, \frac{1}{1+ \gamma / y }\right\} }_{1/2} (1-2\theta ) dF(\theta )+ \int _{1/2}^1 (2\theta -1) dF(\theta )\right] . \end{aligned}$$

As $\theta >1/2$, the difference is increasing in $\gamma \in (1/y,y)$. $\square$

Note that if $\gamma =y$, $v_{R,1}(y)-v_{R,-1}(y)=-k_{1}\int _{\frac{y^{2}}{1+y^{2}}}(2\theta -1)dF(\theta )+k_{-1}\int (2\theta -1)dF(\theta )$, which is positive by the assumption. Similarly, if $\gamma =1/y$, $v_{R,1}(1/y)-v_{R,-1}(1/y)=-k_{1}\int (2\theta -1)dF(\theta )+k_{-1}\int _{\frac{y^{2}}{1+y^{2}}}(2\theta -1)dF(\theta )$, which is negative because $k_{1}\geqslant k_{-1}$. Thus, there is a $\gamma ^{*}\in (1/y,y)$ such that $v_{R,1}(\gamma ^{*})=v_{R,-1}(\gamma ^{*})$. By Claim 1, such $\gamma ^{*}$ is unique in (1/y, y).²⁶$\square$

Proof of Proposition 1

As in the proof of Lemma 3, the fixed point of $\varphi$ characterizes the BNE.

Suppose that $v_{R,1}(\gamma ^{*})=v_{R,-1}(\gamma ^{*})>1/2$. Therefore, by Claim 1, there exists a $\bar{\delta }>0$ such that for each $\delta < \bar{\delta }$ and $\gamma \in (\gamma ^{*}, \gamma ^{*}+ \delta )$, $v _{R,1}(\gamma )>v _{R,-1}(\gamma )>1/2$ and each $\gamma \in (\gamma ^{*}- \delta ,\gamma ^{*})$, $v _{R,-1}(\gamma )>v _{R,1}(\gamma )>1/2$. Then, for a sufficiently large n, if $\gamma \in (\gamma ^{*}, \gamma ^{*}+ \delta )$, $\varphi (\gamma )= \frac{1-q}{q } \left[ \frac{v _{R,-1} (\gamma )(1-v _{R, -1}(\gamma ))}{ v _{R,1}(\gamma ) (1-v _{R, 1}(\gamma ))}\right] ^n>\gamma ^{*}+ \delta$ and if $\gamma \in (\gamma ^{*}- \delta ,\gamma ^{*})$, $\varphi (\gamma )= \frac{1-q}{q } \left[ \frac{v _{R,-1} (\gamma )(1-v _{R, -1}(\gamma ))}{ v _{R,1}(\gamma ) (1-v _{R, 1}(\gamma ))}\right] ^n<\gamma ^{*}- \delta$. Then, by the intermediate value theorem, we can find a fixed point of $\varphi$ in $(\gamma ^{*}- \delta ,\gamma ^{*}+ \delta )$. Taking a sufficiently small $\delta$ implies that there is a fixed point of $\varphi$ that is sufficiently close to $\gamma ^{*}$ when $n\rightarrow \infty$. Therefore, as $n\rightarrow \infty$, $v _{R,\omega }\rightarrow v^{*}>1/2$ for each $\omega$. $\square$

Proof of Proposition 2

Recall that under the sincere voting strategy, each voter determines which candidate to vote for as if he is a dictator (Austen-Smith and Banks 1996). Under the sincere voting strategy, as in Lemma  2, each voter’s behavior is derived as follows.

• 1. If $(t,\sigma )=(1,1)$, he votes for R if $\theta < \frac{ \bar{\gamma }y}{1+ \bar{\gamma }y }$, and he votes for D if $\theta > \frac{ \bar{\gamma }y}{1+ \gamma y }$,

• 2. If $(t,\sigma )=(1,-1)$, he votes for R if $\theta > \frac{1}{1+ \bar{\gamma }y }$, and he votes for D if $\theta < \frac{1}{1+ \bar{\gamma }y }$ .

• 3. If $(t,\sigma )=(-1,1)$, he votes for R if $\theta > \frac{ \bar{\gamma }/y}{ 1+ \bar{\gamma }/y }$, and he votes for D if $\theta < \frac{ \bar{\gamma }/y}{ 1+ \bar{\gamma }/y }$.

• 4. If $(t,\sigma )=(-1,-1)$, he votes for R if $\theta < \frac{1}{1+ \bar{\gamma }/y }$, and he votes for D if $\theta > \frac{1}{1+ \bar{\gamma }/y }$,

where $\bar{\gamma }= \frac{1-q}{q}$. If $q\approx 1$, $\bar{\gamma }\approx 0$. Therefore, as $\theta \in (1/2,1)$, type $t= 1$ never votes for R. As we know that type $t= 0$ never votes for R, only type $t= -1$ votes for R. Hence, the vote share of R is less than 1/2. The case for $q\approx 0$ is similar. $\square$

Proof of Proposition 3

We first prepare the following claim.

Claim 2

Suppose that $k_{1}=k_{-1}$ and $F''<0$. Then $v_{R,1}(\gamma )+v_{R,-1}(\gamma )$ is single-peaked, and its peak is $\gamma =1$.

Proof of Claim 2

To show this result, we consider three cases.

• Case (1) $\gamma \in [1/y,y]$: In this case,

  $$\begin{aligned} v_{R,1}(\gamma )+v_{R,-1}(\gamma )=k \left( 2+F\left( \frac{ \gamma y}{1+ \gamma y}\right) +F\left( \frac{y}{y+ \gamma }\right) \right) . \end{aligned}$$

  By differentiating the above equation with respect to $\gamma$, we obtain

  $$\begin{aligned} k \left[ F'\left( \frac{ \gamma y}{1+ \gamma y}\right) \frac{y}{(1+ \gamma y)^2}-F'\left( \frac{y}{y+ \gamma }\right) \frac{y}{(y+ \gamma )^2}\right] . \end{aligned}$$

  Note the following two facts.

  $$\begin{aligned} \frac{ \gamma y}{1+ \gamma y}> \frac{y}{y+ \gamma } \iff \gamma>1,\\ \frac{y}{(1+ \gamma y)^2}<\frac{y}{(y+ \gamma )^2}\iff \gamma >1. \end{aligned}$$

  Then, as $F''<0$, $\frac{\partial [v_{R,1}(\gamma )+v_{R,-1}(\gamma )]}{\partial \gamma }>0$ if and only if $\gamma <1$. Therefore, $v_{R,1}(\gamma )+v_{R,-1}(\gamma )$ is maximized at $\gamma =1$.

• Case (2) $\gamma >y$: In this case,

  $$\begin{aligned} v_{R,1}(\gamma )+v_{R,-1}(\gamma )=k \left( 2+F\left( \frac{ \gamma y}{1+ \gamma y}\right) - F\left( \frac{ \gamma }{y+ \gamma }\right) \right) . \end{aligned}$$

  By differentiating the above equation with respect to $\gamma$, we obtain

  $$\begin{aligned} k \left[ F'\left( \frac{ \gamma y}{1+ \gamma y}\right) \frac{y}{(1+ \gamma y)^2}-F'\left( \frac{\gamma }{y+ \gamma }\right) \frac{y}{(y+ \gamma )^2}\right] . \end{aligned}$$

  As $\frac{ \gamma y}{1+ \gamma y}> \frac{\gamma }{y+ \gamma }$ and $F''<0$, $\frac{\partial [v_{R,1}(\gamma )+v_{R,-1}(\gamma )]}{\partial \gamma }<0$.

• Case (3) $\gamma <1/y$: In this case,

  $$\begin{aligned} v_{R,1}(\gamma )+v_{R,-1}(\gamma )=k \left( 2-F\left( \frac{ 1}{1+ \gamma y}\right) + F\left( \frac{ 1}{1+ \gamma /y}\right) \right) . \end{aligned}$$

  By differentiating the above equation with respect to $\gamma$,

  $$\begin{aligned} k \left[ F'\left( \frac{ 1}{1+ \gamma y}\right) \frac{y}{(1+ \gamma y)^2}-F'\left( \frac{1}{1+ \gamma /y}\right) \frac{y}{(y+ \gamma )^2}\right] . \end{aligned}$$

  Then, we know that $\frac{\partial [v_{R,1}(\gamma )+v_{R,-1}(\gamma )]}{\partial \gamma }>0$.

By cases (1)–(3), $v_{R,1}(\gamma )+v_{R,-1}(\gamma )$ is single-peaked, and its peak is $\gamma =1$. $\square$

By this claim, because we know that $v_{R,1}(1)+v_{R,-1}(1)=\frac{k}{2}(1+F(\frac{y}{1+y}))<1/2$, for each $\gamma \in \mathbb {R}_{+}$, $v_{R,1}(\gamma )+v_{R,-1}(\gamma )<1/2$.

Let $v_{R, \omega }$ be the equilibrium probability with which a given voter votes for candidate R in state $\omega \in \{-1,1\}$. To complete the proof, suppose by contradiction that there is a BNE in which $\max \{v_{R,1},v_{R,-1}\} \geqslant 1/2$ for a sufficiently large n. As $v_{R,1}(\gamma )+v_{R,-1}(\gamma )<1/2$ for each $\gamma$, $\min \{v_{R,1},v_{R,-1}\}<1/2$ in the BNE. Given this, without loss of generality, we assume that $v_{R,1}\geqslant 1/2>v_{R,-1}$. Hence, because $v_{R,1}(\gamma )+v_{R,-1}(\gamma )<1/2$ for each $\gamma$,

$$\begin{aligned} 1-v_{R,-1}>v_{R,1}\geqslant 1/2\geqslant 1-v_{R,1}>v_{R,-1}, \end{aligned}$$

which implies that $(1-v_{R,-1})v_{R,-1}<(1-v_{R,1})v_{R,1}$. By the equilibrium condition,

$$\begin{aligned} \gamma =\varphi (\gamma )= \frac{1-q}{q}\left[ \frac{v_{R,-1}(\gamma )(1-v_{R,-1}(\gamma ))}{v_{R,1}(\gamma )(1-v_{R,1}(\gamma ))}\right] ^n. \end{aligned}$$

Then, as $n\rightarrow \infty$, $\varphi (\gamma )\rightarrow 0$, and, thus, $\gamma \rightarrow 0$ in the BNE. As $\lim _{\gamma \rightarrow 0}v_{R,1}(\gamma )=k<1/2$, it contradicts the assumption that $v_{R,1}\geqslant 1/2$. $\square$

Proof of Proposition 4

Note that as $\gamma \rightarrow 0$, $\lim _{ \gamma \rightarrow 0}v _{R,1}(\gamma )= \lim _{ \gamma \rightarrow 0}v _{R,-1}(\gamma )= k<1/2$.

Note also that for each $\gamma \in \mathbb {R}_{+}$, $v _{R,\omega }(\gamma )\in ( \underline{ a }, \overline{ a })$ for some $\underline{ a }, \overline{ a }$ such that $0< \underline{ a }< \overline{ a }<1$. Thus, $\left[ \frac{v _R(-1) (1-v _R( -1))}{ v _R(1) (1-v _R( 1))}\right] ^n \in (\underline{ b }, \overline{ b })$ such that $0< \underline{ b }< \overline{ b }<\infty$. Therefore, for each $\varepsilon >0$, there exists $\underline{ q }$ such that for each $q< \underline{ q }$, $\varphi (\gamma )< \varepsilon$ for each $\gamma$. Then, each fixed point of $\varphi$ is also less than $\varepsilon$. By the continuity of $v_{R, \omega }(\gamma )$, for a sufficiently small $\delta >0$, $\max _{ \omega } v _{R, \omega }< k+ \delta <1/2$.

A similar argument is valid for the case of a sufficiently large q. $\square$

Proof of Proposition 5

(1) The BNE with property (a) is shown in Proposition  1. To complete the proof, we prepare the following claim.

Claim 3

Suppose that $k_{1}=k_{-1}$. Then, $v_{R,1}(\gamma )> v_{R,-1}(\gamma )$ if $\gamma \in (0,1/y]$, and $v_{R,1}(\gamma )\geqslant v_{R,-1}(\gamma )$ if $\gamma \in [y,\infty )$.

Proof of Claim 3

Consider the case in which $\gamma \in (0,1/y]$. Then, $v_{R,1}(\gamma )-v_{R,-1}(\gamma )$ is

$$\begin{aligned} \frac{k}{2}\left[ \int _{\frac{1}{1+ \gamma y}}(1- 2\theta )dF(\theta )+\int _{\frac{y}{y+\gamma }}(2\theta -1)dF(\theta )\right] . \end{aligned}$$

As $y>1$, $\frac{y}{y+\gamma }>\frac{1}{1+ \gamma y}$. Thus, $v_{R,1}(\gamma )-v_{R,-1}(\gamma )< 0$. Consider the case in which $\gamma \in [y,\infty )$. Then, $v_{R,1}(\gamma )-v_{R,-1}(\gamma )$ is

$$\begin{aligned} \frac{k}{2}\left[ \int _{\frac{\gamma y}{1+ \gamma y}}(1- 2\theta )dF(\theta )+\int _{\frac{\gamma }{y+\gamma }}(2\theta -1)dF(\theta )\right] . \end{aligned}$$

As $y>1$, $\frac{\ \gamma y}{1+\gamma y}>\frac{\gamma }{y+ \gamma }$. Thus, $v_{R,1}(\gamma )-v_{R,-1}(\gamma )dF(\theta )> 0$. $\square$

By this claim, and Claim 1, $v_{R,1}(\gamma )>v_{R,-1}(\gamma )$ if and only if $\gamma >1$.

Note that $v_{R,1}(0)+v_{R,-1}(0)=\lim _{\gamma \rightarrow \infty }v_{R,1}(\gamma )+v_{R,-1}(\gamma )=k<1$. Note also that $v_{R,1}(1)+v_{R,-1}(1)=k(1+F(\frac{y}{1+y}))>1$. Then, by Claim 2, there is unique $\gamma _1, \gamma _{-1}$ ($\gamma _{1}>1>\gamma _{-1}$) such that

$$\begin{aligned}&v_{R,1}(\gamma _1)+v_{R,-1}(\gamma _1)=1, \quad v_{R,1}(\gamma _1)>1/2>v_{R,-1}(\gamma _1),\\&v_{R,1}(\gamma _{-1})+v_{R,-1}(\gamma _{-1})=1, \quad v_{R,1}(\gamma _{-1})<1/2<v_{R,-1}(\gamma _{-1}). \end{aligned}$$

Consider $\gamma _{1}$. Note that the BNE is characterized by the fixed point of $\varphi (\gamma )=\frac{1-q}{q}\left[ \frac{(1-v_{R,-1}(\gamma ))v_{R,-1}(\gamma )}{(1-v_{R,1}(\gamma ))v_{R,1}(\gamma )}\right] ^{n}$. Note also that by Claim 2 and $\gamma _{1}>1$, $v_{R,1}(\gamma )+v_{R,-1}(\gamma )$ is increasing in the neighborhood of $\gamma =\gamma _{1}$. This implies that there is small $\delta$ such that if $\gamma \in (\gamma _{1}, \gamma _{1}+\delta )$, $v_{R,1}(\gamma )+v_{R,-1}(\gamma )>1$. Then, because $v_{R,1}(\gamma _{1})=1-v_{R,-1}(\gamma _{1})>1/2$, $(1-v_{R,-1}(\gamma ))v_{R,-1}(\gamma )>(1-v_{R,1}(\gamma ))v_{R,1}(\gamma )$. Similarly, if $\delta$ is sufficiently small and $\gamma \in (\gamma _{1}-\delta , \gamma _{1})$, $(1-v_{R,-1}(\gamma ))v_{R,-1}(\gamma )<(1-v_{R,1}(\gamma ))v_{R,1}(\gamma )$. Then, by using the same logic as in the proof of Proposition  1, there is a sequence of BNEs in which $v_{R,1}\rightarrow v_{R,1}(\gamma _{1})$ and $v_{R,-1}\rightarrow v_{R,-1}(\gamma _{1})$.

Similarly, we can also prove that there is a sequence of BNEs in which $v_{R,1}\rightarrow v_{R,1}(\gamma _{-1})$ and $v_{R,-1}\rightarrow v_{R,-1}(\gamma _{-1})$, which completes the proof of (1).

(2) The remaining type of BNE has $\max \{\lim _{n\rightarrow \infty }v_{R,-1},\lim _{n\rightarrow \infty }v_{R,1}\}<1/2$. Then, suppose by contradiction that there is a sequence of BNE in which $v_{R,\omega }\rightarrow v_{R,\omega }(\widehat{\gamma })<1/2$ for each $\omega$. Note that if $\gamma =1$, $v_{R,\omega }(1)=\frac{k}{2}(1+F(\frac{y}{1+y}))>1/2$, and thus, $\widehat{\gamma }\ne 1$. Recall that each BNE is characterized by the fixed point of $\varphi (\gamma )$. This implies that there is a sequence of fixed points that converges to $\widehat{\gamma }$ as $n\rightarrow \infty$.

First, note that $\varphi (0)=\varphi (\infty )=\frac{1-q}{q}$. Thus, neither 0 nor $\infty$ is a fixed point of $\varphi$. Consider the case that $\widehat{\gamma }\in (1,\infty )$. As we know that if $\gamma \in (1,\infty )$, $v_{R,1}(\gamma )> v_{R,-1}(\gamma )$. Furthermore, because $v_{R,\omega }(\widehat{\gamma })<1/2$ for each $\omega$, $v_{R,1}(\widehat\gamma )(1-v_{R,1}(\widehat\gamma ))>v_{R,-1}(\widehat\gamma )(1-v_{R,-1}(\widehat\gamma ))$ for $\widehat\gamma \in (1,\infty )$. Then, as $n\rightarrow \infty$, $\varphi (\gamma )\rightarrow 0$ for each sequence  converges to $\widehat\gamma \in (1,\infty )$, which is a contradiction of the fact that the sequence of fixed points converges to $\widehat{\gamma }\in (1,\infty )$.

Similarly, we also show that the case for $\widehat{\gamma }\in (0,1)$ has a contradiction, which completes the proof. $\square$

1.2 A.2. Proof of Proposition 6

For the BNE when $x _i=0$ and $x _j\ne 0$, $i,j\in \{R,D\}$, we consider a BNE such that $\gamma \rightarrow 1$ as $n\rightarrow \infty$. Existence is guaranteed by Proposition 1 for any common prior belief of voters such that $\mathrm {Pr}(\omega = 1)\in (0,1)$.

Case (1) $\beta < q$. After receiving her signal, for each $i\in \{R,D\}$, candidate i’s posteriors to the event for which $\omega =1$ are

$$\begin{aligned} \mathrm {Pr}(\omega =1\mathrel {|}\sigma _i=1)&=\frac{ q \beta }{q \beta +(1-q)(1-\beta )}>1/2,\\ \mathrm {Pr}(\omega =1\mathrel {|}\sigma _i=-1)&=\frac{q(1- \beta )}{q(1- \beta )+(1-q)\beta }>1/2. \end{aligned}$$

Now, we show that there is a PBNE in which $x_R(1)=x_R(-1)=1$ and $x_D(1)=x_D(-1)=-1$. By Lemma 1, under the strategy profile, each candidate wins with probability 1/2. As $\mathrm {Pr}(\omega =1\mathrel {|}\sigma _i)>1/2$, candidate D has no incentive to deviate to $x_D=1$. Candidate R also has no incentive to deviate for the same reason.

Now, consider a deviation to $x_i=0$. Note that, under the voters’ beliefs after observing the candidates’ choices (before receiving the voters’ signals), the posterior $\mathrm {Pr}(\omega =1\mathrel {|}x_{R}, x_{D})$ is a convex combination of $\mathrm {Pr}(\omega =1\mathrel {|}\sigma _i=1)\in (0,1)$ and $\mathrm {Pr}(\omega =1\mathrel {|}\sigma _i=-1)\in (0,1)$, $i\in \{R,D\}$. For a sufficiently large n, by Proposition 1, the deviating candidate’s winning probability is less than 1/2. Therefore, neither candidate has an incentive to deviate to $x_i=0$, and the proof is complete.

Case (2) $\beta >q$. After receiving her signal, candidate D’s posteriors to the event for which $\omega =1$ are

$$\begin{aligned} \mathrm {Pr}(\omega =1\mathrel {|}\sigma _D=1)&=\frac{ q \beta }{q \beta +(1-q)(1-\beta )}>1/2,\\ \mathrm {Pr}(\omega =1\mathrel {|}\sigma _D=-1)&=\frac{q(1- \beta )}{q(1- \beta )+(1-q)\beta }<1/2. \end{aligned}$$

Now, we show that there is a PBNE in which $x_R(1)=1$, $x_{R}(-1)=1$, $x_D(1)=-1$, and $x_D(-1)=1$. By Lemma 1, under the strategy profile, each candidate wins with probability 1/2 in each state.

Let $i\in \{R,D\}$. Consider a deviation to $x_{i}=0$. As in case (1), we can prove that, for a sufficiently large n, this deviation is unprofitable.

The other deviation is also unprofitable, as the winning probability is the same, and the other policy is less desirable for candidate i. $\square$

1.3 A.3. Proof of Proposition 7

(1) We show that there is a PBNE in which $x_{i}(\sigma )=0$ for each $i\in \{R,D\}$ and $\sigma \in \{-1,1\}$. For candidate D’s deviation, assume that a voter’s off-equilibrium path belief places probability 1 on $\sigma _D=-x_D$ if $x_D\ne 0$. For candidate R’s deviation, we also assume that a voter’s off-equilibrium path belief places probability 1 on $\sigma _R=x_R$ if $x_R\ne 0$.

Consider candidate R’s deviation. Let $\overline{q}$ and $\underline{q}$ be the values that are obtained in Proposition  4. Then, by the assumption, under the voters’ belief after observing the candidates’ choices (before receiving the voters’ signals), for a sufficiently large $\beta _R$,

$$\begin{aligned} P(\omega = 1\mathrel {|}x _R= 1)&= \frac{q \beta _R}{q \beta _R+ (1-q) (1-\beta _R )}> \overline{q}\\ P(\omega = 1\mathrel {|}x _R= -1)&= \frac{q (1-\beta _R)}{q (1-\beta _R)+ (1-q) \beta _R } < \underline{q}. \end{aligned}$$

By Proposition 4, the above inequalities imply that candidate R’s winning probability is less than 1/2. Note that, in the original strategy profile, each candidate wins with probability 1/2. When $\xi$ is sufficiently small, this deviation is unprofitable. The same discussion applies to any deviation of candidate D. Therefore, it is a PBNE.

(2) Let $q_{i,\sigma }$ be candidate i’s updated belief about the probability of $\omega =1$ after receiving signal $\sigma$. We fix $\beta _R$ such that

$$\begin{aligned} q_{R,1}&{:}{=}\frac{q \beta _R}{q \beta _R+ (1-q) (1-\beta _R )}= \beta _R> \overline{q}, \end{aligned}$$

(5)

$$\begin{aligned} q_{R,-1}&{:}{=}\frac{q (1-\beta _R)}{q (1-\beta _R)+ (1-q) \beta _R } =1- \beta _R< \underline{q}. \end{aligned}$$

(6)

Then, by (1), there is a PBNE such that $x _i(\sigma )= 0$ for each $i\in \{R,D\}$ and $\sigma \in \{1,-1\}$.

Step 1: There is no PBNE in which $x_{D}(1)\ne x_{D}(-1)$. Consider the strategy $x_{D}(1)\ne x_D(-1)$. Then, for each candidate D’s choice $x_{D}\in \{x_D(1),x_D(-1)\}$, voters’ beliefs place probability 1 on the event that $\sigma _{D}=x_D^{-1}(x_D)$. Let $P(\sigma _R\mathrel {|}x _R)$ be the probability that candidate R receives signal $\sigma _R\in \{1,-1\}$ under the voters’ (possibly off-equilibrium-path) beliefs after observing candidate R’s choice $x _R$. For a sufficiently large $\beta _D$, voters’ beliefs after observing the candidates’ choices (before receiving the voters’ signals) are calculated as

$$\begin{aligned}&\mathrm {Pr}(\omega =1\mathrel {|}x_{D}=x_D(1), x _R)=\frac{ q \beta _D X _1}{q \beta _DX _1+(1-q)(1-\beta _D)X _{ -1}}> \overline{q}, \quad \text { for each } x_R\\&\mathrm {Pr}(\omega =1\mathrel {|}x_{D}=x_D(-1),x _R)=\frac{q(1- \beta _D)X _1}{q(1- \beta _D)X _1+(1-q)\beta _D X _{ -1}}< \underline{q},\quad \text { for each } x_R\\&X _ 1 = \beta _R P ( \sigma _R= 1\mathrel {|}x _R)+ (1- \beta _R ) P ( \sigma _R= -1\mathrel {|}x _R)\in (1- \beta _R,\beta _R) \\&X _ {-1} = (1-\beta _R)P ( \sigma _R= 1\mathrel {|}x _R)+ \beta _R P ( \sigma _R= -1\mathrel {|}x _R)\in (1- \beta _R,\beta _R). \end{aligned}$$

The last two inequalities follow from the fact that $\max _{\sigma \in \{-1,1\}}\{ P(\sigma _R=\sigma \mathrel {|}x _R)\}>0$ and $\beta _R\in (0,1)$. We consider the following cases.

• Case 1. $x_D(\sigma )\ne 0$ for each $\sigma \in \{-1,1\}$. In this case, by Proposition 4, if $x_{R}(\sigma )=0$, candidate R wins with some probability greater than 1/2. Otherwise, by Lemma 1, she wins with probability 1/2. If $\xi >0$ is sufficiently small, $x_{R}(\sigma )=0$ is her best response. Then, in turn, when $\xi >0$ is sufficiently small, for candidate D, $x_{D}(\sigma )=0$, $\sigma \in \{-1,1\}$ is also her best response.

• Case 2. $x_D(\sigma )=0$ for some $\sigma \in \{-1,1\}$. Without loss of generality, we assume that $x_D(1)=0$. By assumption, $x_D(-1)\ne 0$. In this case, if $x_R=0$, candidate R’s winning probability is

  $$\begin{aligned} P(\sigma _D=-1\mathrel {|}\sigma _R)w_R+P(\sigma _D=1\mathrel {|}\sigma )\frac{1}{2}, \end{aligned}$$

  where $w_R>1/2$ by Proposition 4. However, if $x_R\ne 0$, candidate R’s winning probability is

  $$\begin{aligned} P(\sigma _D=-1\mathrel {|}\sigma _R)1/2+P(\sigma _D=1\mathrel {|}\sigma )w'_R, \end{aligned}$$

  where $w_R'<1/2$. If $\xi >0$ is sufficiently small, $x_{R}(\sigma )=0$ is her best response. Then, in turn, when $\xi >0$ is sufficiently small, for candidate D, $x_{D}(\sigma )=0$, $\sigma \in \{-1,1\}$ is also her best response.

Therefore, in each PBNE, candidate D does not choose a separating strategy.

Step 2: There is no PBNE in which $x_{D}(1)= x_{D}(-1)\ne 0$. To show this result, consider a strategy in which $x_{D}(1)= x_{D}(-1)\ne 0$. Without loss of generality, we consider the case in which $x_{D}(1)=x_{D}(-1)=1$. Suppose by contradiction that the following strategy profiles of the candidates are PBNE.

• Case (1) Candidate R takes a strategy such that $x_{R}(1)=x_{R}(-1)\ne 0$. Then, D’s winning probability is 1/2. By Lemma 1, candidate D’s deviation such that $x_{D}(1)=-1$ gives D a winning probability of 1/2 for each BNE. Then, by her policy preferences, $x_{D}(1)=-1$ is a profitable deviation for candidate D.

• Case (2) Candidate R takes a strategy such that $x_{R}(\sigma )=0$ for each $\sigma$. Let $w_{R}(\omega )$ be R’s winning probability in state $\omega$ and recall that $q_{i,\sigma }$ is candidate i’s updated belief about the probability of $\omega =1$ after receiving signal $\sigma$. If $x_R=0$, candidate R’s expected utility is

  $$\begin{aligned}{}[q_{R,\sigma } w_{R}(1)+(1-q_{R,\sigma })w_{R}(-1)](1-\xi L(1)) -(1-q_{R,\sigma })(1-w_{R}(-1))\xi L(2). \end{aligned}$$

  However, by deviating to $x_R(\sigma )=\sigma$, candidate R’s expected utility becomes

  $$\begin{aligned} \left\{ \begin{array}{lll} \frac{1}{2}-(1-q_{R,1})\xi L(2) &{} \text {if} &{} \sigma =1,\\ \frac{1}{2}-\frac{1}{2} \xi L(2) &{} \text {if} &{} \sigma =-1.\\ \end{array}\right. \end{aligned}$$

  Therefore, in each PBNE,

  $$\begin{aligned}&[q_{R,1} w_{R}(1)+(1-q_{R,1})w_{R}(-1)](1-\xi L(1))-(1-q_{R,1})(1-w_{R}(-1))\xi L(2) \nonumber \\&\quad \geqslant \frac{1}{2}-(1-q_{R,1})\xi L(2), \end{aligned}$$

  (7)
  $$\begin{aligned}&[q_{R,-1} w_{R}(1)+(1-q_{R,-1})w_{R}(-1)](1-\xi L(1) )-(1-q_{R,-1})(1-w_{R}(-1))\xi L(2) \nonumber \\&\quad \geqslant \frac{1}{2}-\frac{1}{2}\xi L(2). \end{aligned}$$

  (8)

  By adding (7) into (8),

  $$\begin{aligned} -1+[(q_{R,1} +q_{R,-1})w_{R}(1)+(2-q_{R,1}-q_{R,-1})w_{R}(-1)](1-\xi L(1))\nonumber \\ +[(1/2-q_{R,1})-(2-q_{R,1}-q_{R,-1})(1-w_{R}(-1))]\xi L(2) \geqslant 0. \end{aligned}$$

  (9)

  Consider candidate D’s incentive. Let $u_D(\sigma )$ be candidate D’s expected utility when she receives signal $\sigma _D=\sigma$.

  $$\begin{aligned} u_D(\sigma )&=[1-q_{D,\sigma } w_{R}(1)-(1-q_{D,\sigma })w_{R}(-1)]\\&\quad -\xi [q_{D,\sigma }(1-w_{R}(1)) L(2)+(q_{D,\sigma } w_{R}(1)+(1-q_{D,\sigma })w_{R}(-1)) L(1)] \end{aligned}$$

  In each PBNE, it is necessary that $\min \{u_D(1),u_D(-1)\}\geqslant 1/2-\xi L(1)$. Then, we obtain

  $$\begin{aligned} u_D(1)+u_D(-1)&=1-(q_{D,-1}+q_{D,1})w_R(1)(1+\xi L(1))\nonumber \\&\quad -(2-q_{D,-1}-q_{D,1})w_R(-1)(1+\xi L(1))\nonumber \\&\quad +\xi [2L(1)-(1-w_R(1))L(2)]\geqslant 0. \end{aligned}$$

  (10)

  Adding (9) to (10) yields

  $$\begin{aligned} \xi (1-w_R(1)-w_R(-1)) [2 L(1)- L(2)] \geqslant q_{R,1}-1/2. \end{aligned}$$

  As $(1-w_R(1)-w_R(-1)) [2 L(1)- L(2)]$ is bounded and $q_{R,1}>1/2$, for a sufficiently small $\xi$, the above inequality is violated. This result implies that there is a profitable deviation.

• Case (3) Candidate R takes a strategy such that $x _R(1)\ne x _R(-1)$. Then, as $\beta _R$ is high so that (5) and (6) are satisfied, under the voters’ common belief after observing the candidates’ choices,

  $$\begin{aligned} P(\omega = 1\mathrel {|}x _R= x _R(1),x_{D})&= \frac{q \beta _R}{q \beta _R+ (1-q) (1-\beta _R )}> \overline{ q },\\ P(\omega = 1\mathrel {|}x _R= x _R(-1),x_{D})&= \frac{q (1-\beta _R)}{q (1-\beta _R)+ (1-q) \beta _R } < \underline{ q }. \end{aligned}$$

  Note that, for some $\sigma \in \{-1,1\}$, $x_{R}(\sigma )\in \{-1,1\}$. Then, by Proposition 4 and Lemma 1, candidate D’s winning probability is less than or equal to 1/2. For each signal $\sigma \in \{-1,1\}$, consider a deviation such that $x_{D}(\sigma )=0$. We consider the following three cases.

  • a) Suppose that voters have off-equilibrium-path beliefs such that $P(\sigma _D= 1\mathrel {|}x _D= 0)= 1$. Then, as shown in case (1), $P(\omega = 1\mathrel {|}x _R, X _D= 0)> \overline{ q }$. Note that $x _R(\sigma )\ne 0$ for some $\sigma$. Given this result and by Proposition refconvmed and Lemma 1, candidate D’s winning probability is higher than 1/2. This is a profitable deviation for candidate D.

  • b) The case in which $P(\sigma _D= 1\mathrel {|}x _D= 0)= 0$ is identical to the previous case.

  • c) Suppose that voters have off-equilibrium path beliefs such that $P(\sigma _D= 1\mathrel {|}x _D= 0)= 1/2$. Then, in each state,

    $$\begin{aligned} P(\omega = 1\mathrel {|}x _R= x _R(1))&= \frac{q \beta _R}{q \beta _R+ (1-q) (1-\beta _R )}= \beta _R> \overline{ q },\\ P(\omega = 1\mathrel {|}x _R= x _R(-1))&= \frac{q (1-\beta _R)}{q (1-\beta _R)+ (1-q) \beta _R } =1- \beta _R< \underline{ q }. \end{aligned}$$

    Given this result and by Proposition 4, candidate D’s winning probability is higher than 1/2. This is a profitable deviation for candidate D.

Therefore, each case admits a profitable deviation and, hence, there is no PBNE in which $x_{D}(1)=x_{D}(-1)\ne 0$.

Step 3. Completing the proof. By steps 1 and 2, as we focus on pure strategies, in each PBNE, $x_{D}(\sigma _{D})=0$ for each $\sigma _{D}\in \{-1,1\}$.

Now, consider candidate R’s behavior. Suppose that $x_{R}(\sigma )=1$ for each $\sigma$. Recall that $w_{R}(\sigma )$ is the probability with which candidate R wins. Then, we will prove that $w_{R}(1)=w_{R}(-1)=1/2$.

To show this result, suppose by a contradiction that $w_{R}(\sigma )\ne 1/2$ for some $\sigma$. We consider the following cases.

• 1. $w_{R}(1)>1/2$. Then, as $\beta _{D}$ is large enough, if candidate D receives the signal $\sigma _{D}=1$, under her belief, her winning probability is approximately $1-w_{R}(1)<1/2$. By deviating to $x_{D}(1)=-1$, her winning probability becomes 1/2. As $x= -1$ is candidate D’s preferred policy, both her office and policy motivations improve. Therefore, this deviation is profitable, a contradiction.

• 2. $w_{R}(-1)>1/2$. This case is symmetric to the previous case.

By the above discussion, we know that $w_{R}(\sigma ) \leqslant 1/2$ for each $\sigma \in \{-1,1\}$, and, by assumption, $\min \{w_{R}(1),w_{R}(-1)\}<1/2$. Suppose that candidate R receives the signal $\sigma$. Then, under candidate R’s belief, her winning probability is $q_{R, \sigma }w_{R}(1)+(1- q_{R, \sigma })w_{R}(-1)<1/2$. Then, by deviating to $x_{R}(1)=0$, the winning probability becomes 1/2. For a sufficiently small $\xi >0$, this deviation is profitable for candidate R, a contradiction.

Then, we can conclude that $w_{R}(1)=w_{R}(-1)=1/2$. In this case, candidate D also has an incentive to deviate so that $x_{D}(-1)=1$. In this case, although candidate D’s winning probability remains 1/2, her utility from her policy motivation increases. Thus, there is no PBNE in which $x_{R}(\sigma )=1$.

The case for $x_{R}(\sigma )=-1$ for each $\sigma$ is identical.

Last, we consider the case for $x _R(1)\ne x _R(-1)$. Then, because $x_{R}(\sigma )\in \{-1,1\}$ for some $\sigma \in \{-1,1\}$, as in case (3) in step 2, we can prove that R’s winning probability is less than 1/2. Then, by deviating so that $x _R(\sigma )= 0$, R achieves a winning probability of 1/2, which is a profitable deviation if $\xi >0$ is sufficiently small. Therefore, in each PBNE, $x _R(\sigma )= 0$ for each $\sigma \in \{-1,1\}$. $\square$

1.4 A.4. Proof of Proposition 8

First, note that a type 0 voter votes for candidate D. Consider the strategy profile such that no voter votes for candidate L. Now consider a type 1 voter. For notational simplicity, we let $\mathrm {Pr}(\omega )=\mathrm {Pr}(\omega \mathrel {|}\sigma , \theta )$. Then, the expected utility of voting for candidate R is

$$\begin{aligned} u_{1R}&=\mathrm {Pr}(1)[-L(2) \mathrm {Pr}( z_R\geqslant n \mathrel {|}\omega =1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =1)]\\&\quad +\mathrm {Pr}(-1)[-L(0) \mathrm {Pr}( z_R\geqslant n \mathrel {|}\omega =-1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =-1)]. \end{aligned}$$

Similarly, the expected utility of voting for D is

$$\begin{aligned} u_{1D}&=\mathrm {Pr}(1)[-L(2) \mathrm {Pr}( z_R\geqslant n+1 \mathrel {|}\omega =1) -L(1)\mathrm {Pr}( n\geqslant z_R \mathrel {|}\omega =1)]\\&\quad +\mathrm {Pr}(-1)[-L(0) \mathrm {Pr}( z_R\geqslant n+1 \mathrel {|}\omega =-1) -L(1)\mathrm {Pr}( n\geqslant z_R \mathrel {|}\omega =-1). \end{aligned}$$

Finally, the expected utility of voting for L is

$$\begin{aligned} u_{1L}&=\mathrm {Pr}(1)[-L(2) \mathrm {Pr}( z_R\geqslant n+1 \mathrel {|}\omega =1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =1)\\&\quad -\frac{L(2)+L(1)}{2} \mathrm {Pr}( z_R=n\mathrel {|}\omega =1)]\\&\quad +\mathrm {Pr}(-1)[-L(0) \mathrm {Pr}( z_R\geqslant n+1\mathrel {|}\omega =-1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =-1)\\&\quad -\frac{L(0)+L(1)}{2} \mathrm {Pr}( z_R=n \mathrel {|}\omega =-1)]. \end{aligned}$$

Note that the probability that candidate L wins is zero because at most one voter votes for L and the number of voters is larger than 5. Then,

$$\begin{aligned} u_{1R}-u_{1D}&=-\mathrm {Pr}(1)(L(2)-L(1))\mathrm {Pr}(z_R=n\mathrel {|}\omega =1)\\&\quad +\mathrm {Pr}(-1)L(1)\mathrm {Pr}(z_R=n\mathrel {|}\omega =-1)\\ u_{1R}-u_{1L}&=\frac{1}{2}\left[ \mathrm {Pr}(1)(L(2)-L(1))\mathrm {Pr}(z_R=n\mathrel {|}\omega =1)\right. \\&\quad \left. +\mathrm {Pr}(-1)L(1)\mathrm {Pr}(z_R=n\mathrel {|}\omega =-1)\right] \\ u_{1L}-u_{1D}&=\frac{1}{2}\left[ \mathrm {Pr}(1)(L(2)-L(1))\mathrm {Pr}(z_R=n\mathrel {|}\omega =1)\right. \\&\quad \left. +\mathrm {Pr}(-1)L(1)\mathrm {Pr}(z_R=n\mathrel {|}\omega =-1)\right] . \end{aligned}$$

If voting for candidate L is strictly optimal, $u_{1R}<u_{1L}$ and $u_{1L}>u_{1D}$. However, these inequalities are incompatible, as $u_{1R}-u_{1L}=u_{1L}-u_{1D}$. Therefore, voting for candidate L is never (unique) optimal. For type $-1$ voters, the same argument is valid. In this case, the situation is reduced to the two-candidate case in which $x_R=-1$ and $x_D=0$. Now, Proposition 1 is applicable. $\square$

1.5 A.5. Proof of Proposition 9

First, note that a type 0 voter votes for candidate D. Consider the strategy profile such that no voter abstains. Now consider a type 1 voter. For notational simplicity, we let $\mathrm {Pr}(\omega )=\mathrm {Pr}(\omega \mathrel {|}\sigma , \theta )$. Then, the expected utility of voting for candidate R is

$$\begin{aligned} u_{1R}&=\mathrm {Pr}(1)[-L(2) \mathrm {Pr}( z_R\geqslant n \mathrel {|}\omega =1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =1)]\\&\quad +\mathrm {Pr}(-1)[-L(0) \mathrm {Pr}( z_R\geqslant n \mathrel {|}\omega =-1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =-1)]. \end{aligned}$$

Similarly, the expected utility of voting for D is

$$\begin{aligned} u_{1D}&=\mathrm {Pr}(1)[-L(2) \mathrm {Pr}( z_R\geqslant n+1 \mathrel {|}\omega =1) -L(1)\mathrm {Pr}( n\geqslant z_R \mathrel {|}\omega =1)]\\&\quad +\mathrm {Pr}(-1)[-L(0) \mathrm {Pr}( z_R\geqslant n+1 \mathrel {|}\omega =-1) -L(1)\mathrm {Pr}( n\geqslant z_R \mathrel {|}\omega =-1). \end{aligned}$$

Finally, the expected utility of abstention is

$$\begin{aligned} u_{1A}&=\mathrm {Pr}(1)[-L(2) \mathrm {Pr}( z_R\geqslant n+1 \mathrel {|}\omega =1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =1)\\&\quad -\frac{L(2)+L(1)}{2} \mathrm {Pr}( z_R=n\mathrel {|}\omega =1)]\\&\quad +\mathrm {Pr}(-1)[-L(0) \mathrm {Pr}( z_R\geqslant n+1\mathrel {|}\omega =-1) -L(1)\mathrm {Pr}( n>z_R \mathrel {|}\omega =-1)\\&\quad -\frac{L(0)+L(1)}{2} \mathrm {Pr}( z_R=n \mathrel {|}\omega =-1)]. \end{aligned}$$

Then, as in the proof of Proposition 8, we can show that abstention is never a strictly optimal choice. Therefore, the situation is reduced to the case with no abstention. Now, Proposition 1 is applicable. $\square$

1.6 A.6. Proof of Proposition 10

Note that for each $\gamma \in \mathbb {R}_{+}$, $v_{R,1}(\gamma )+ v_{R,-1}(\gamma )=k<1$. Therefore, in each BNE, $v_{R,1}+ v_{R,-1}<1$. This result implies that $\min \{v_{R,1} ,v_{R,-1}\}<1/2$. Suppose that $v_{R,1} <1/2 \leqslant v_{R,-1}$ in a BNE. Then, $v_{R,1}<1/2\leqslant v_{R,-1}<1-v_{R,1}$, and, hence, $(1-v_{R,-1})v_{R,-1}>(1-v_{R,1})v_{R,1}$. Recall that the equilibrium condition is

$$\begin{aligned} \gamma =\varphi (\gamma )= \frac{1-q}{q}\left[ \frac{v_{R,-1}(\gamma )(1-v_{R,-1}(\gamma ))}{v_{R,1}(\gamma )(1-v_{R,1}(\gamma ))}\right] ^n. \end{aligned}$$

As $n\rightarrow \infty$, $\gamma \rightarrow 0$. However, this expression implies that $v_{R,-1}\rightarrow \frac{k}{2}<1/2$ as $n\rightarrow \infty$, which is a contradiction. Therefore, we conclude that $v_{R,-1}<1/2$. Replacing $v_{R,1}$ and $v_{R,-1}$, we can also show that $v_{R,1}<1/2$ for a sufficiently large n. $\square$

1.7 A.7. Proof of Proposition 11

The proof has three steps.

Step 1. There exists a $\gamma \in (1,\infty )$ such that $v_{R,1}(\gamma )+v_{R,-1}(\gamma )=1$.

Proof of Step 1

By (1) and (2),

$$\begin{aligned}&v_{R,1}(\gamma )+v_{R,-1}(\gamma )\\&\quad =\frac{k}{2} \left( 2-F_1 \left( \frac{1}{1+ \gamma y}\right) +F_1\left( \frac{ \gamma y}{1+ \gamma y}\right) +F_{-1}\left( \frac{1}{1+ \gamma /y}\right) - F_{-1}\left( \frac{ \gamma /y}{1+ \gamma /y}\right) \right) . \end{aligned}$$

When $\gamma =1$, $v_{R,1}(1)+v_{R,-1}(1)=\frac{k}{2}\left( 2+F_{1}\left( \frac{y}{1+y}\right) +F_{-1}\left( \frac{y}{1+y}\right) \right) >1$. However, as $\gamma \rightarrow \infty$, $\lim _{\gamma \rightarrow \infty }v_{R,1}(\gamma )+v_{R,-1}(\gamma )\rightarrow k<1$. Then, the intermediate value theorem implies that there is a $\gamma >1$ such that $v_{R,1}(\gamma )+v_{R,-1}(\gamma )=1$. $\square$

Note that there is a $\gamma ^*\in \{ \gamma >1:v_{R,1}(\gamma )+v_{R,-1}(\gamma )=1\}$ such that there is a $\bar{\delta }>0$, and for each $\delta <\bar{\delta }$,

$$\begin{aligned} {[}v_{R,1}(\gamma ^*+\delta )+v_{R,-1}(\gamma ^*+\delta )-1][v_{R,1}(\gamma ^*-\delta )+v_{R,-1}(\gamma ^*-\delta )-1]<0. \end{aligned}$$

Without loss of generality, we assume that

$$\begin{aligned} v_{R,1}(\gamma ^*+\delta )+v_{R,-1}(\gamma ^*+\delta )>1>v_{R,1}(\gamma ^*-\delta )+v_{R,-1}(\gamma ^*-\delta ). \end{aligned}$$

Step 2. For each $\gamma >1$, $v_{R,1}(\gamma )>v_{R,-1}(\gamma )$.

Proof of Step 2

We note that

$$\begin{aligned} v_{R,1}(\gamma )-v_{R,-1}(\gamma )&=\frac{k}{2}\Big [\int _{ \frac{1}{1+ \gamma y }} (1-2\theta ) dF_{1}(\theta )+ \int ^{ \frac{\gamma y}{1+ \gamma y} }(2 \theta -1) dF_{1}(\theta )\\&\quad \int ^{ \frac{1}{1+ \gamma / y }} (1-2\theta ) dF_{-1}(\theta )+ \int _{ \frac{\gamma / y}{1+ \gamma /y} } (2\theta -1) dF_{-1}(\theta )\Big ]. \end{aligned}$$

Now, we need to consider two cases.

Case 1. $y\geqslant \gamma >1$.

$$\begin{aligned} v_{R,1}(\gamma )-v_{R,-1}(\gamma )=\frac{k}{2}\left[ \int _{ \frac{ y}{y+ \gamma }} (2 \theta -1) dF_{-1}(\theta )-\int _{ \frac{\gamma y}{1+ \gamma y}}(2 \theta -1)dF_1(\theta )\right] . \end{aligned}$$

As $\frac{ y}{y+ \gamma }<\frac{\gamma y}{1+ \gamma y}$ and $F_{-1}$ first-order stochastically dominates $F_1$, the above equation is positive.

Case 2. $\gamma> y>1$.

$$\begin{aligned} v_{R,1}(\gamma )-v_{R,-1}(\gamma )=\frac{k}{2}\left[ \int _{ \frac{ \gamma }{y+ \gamma }} (2 \theta -1)d F_{-1}(\theta )-\int _{ \frac{\gamma y}{1+ \gamma y}}(2 \theta -1)dF_1(\theta )\right]. \end{aligned}$$

As $\frac{ \gamma }{y+ \gamma }<\frac{\gamma y}{1+ \gamma y}$ and $F_{-1}$ first-order stochastically dominates $F_1$, the above equation is also positive. $\square$

Step 3. Complete the proof. Recall that the equilibrium condition is

$$\begin{aligned} \gamma =\varphi (\gamma )= \frac{1-q}{q } \left[ \frac{v _{R,-1}(\gamma ) (1-v _{R,-1}(\gamma ))}{ v _{R,1}(\gamma ) (1-v _{R,1}(\gamma ))}\right] ^n. \end{aligned}$$

By Steps 1 and 2, as $v_{R,1}(\gamma ^*)+v_{R,-1}(\gamma ^*)=1$ and $v_{R,1}(\gamma ^*)> v_{R,-1}(\gamma ^*)$, $v_{R,1}(\gamma ^*)>1/2> v_{R,-1}(\gamma ^*)$. Note that $a(1-a)$ is single-peaked at $a=1/2$. Note also that for each $\gamma \in (\gamma ^*-\bar{\delta },\gamma ^*)$, $v_{R,1}(\gamma )\in (1/2, 1-v_{R,-1}(\gamma ))$. Then, we have $v _{R,1}(\gamma ) (1-v _{R,1}(\gamma ))>v _{R,-1}(\gamma ) (1-v _{R,-1}(\gamma ))$. Thus, as $n\rightarrow \infty$, for each $\gamma \in (\gamma ^*-\bar{\delta },\gamma ^*)$, $\varphi (\gamma )\rightarrow 0$. Therefore, $\gamma ^*- \bar{\delta }-\varphi (\gamma ^*-\bar{\delta })>0$.

For each $\gamma \in (\gamma ^*,\gamma ^*+\bar{\delta })$, the converse relation holds, and, thus, $\gamma ^*+ \bar{\delta }-\varphi (\gamma ^*+\bar{\delta })<0$. By the intermediate value theorem, there is a $\gamma \in (\gamma ^*-\bar{\delta },\gamma ^*+\bar{\delta })$ such that $\gamma =\varphi (\gamma )$. As $\bar{\delta }\rightarrow 0$, we conclude that there is a BNE sequence in which $\gamma \rightarrow \gamma ^*$. Therefore, in this BNE, for a sufficiently large n, $v_{R,1}>1/2>v_{R,-1}$. $\square$