Development and evaluation of gappy-POD as a data reconstruction technique for noisy PIV measurements in gas turbine combustors

Abstract

Low signal-to-noise in particle image velocimetry (PIV) measurements in systems such as high pressure gas turbine combustors can result in significant data gaps that negatively affect subsequent analysis. Here, gappy proper orthogonal decomposition (GPOD) is evaluated as a method of filling such missing data. Four GPOD methods are studied, including a new method that utilizes a median filter (MF) to adaptively select whether a local missing data point is updated after each iteration. These methods also are compared against local Kriging interpolation. The GPOD methods are tested using PIV data without missing vectors that were obtained in atmospheric pressure swirl flames. Parameters studied include the turbulence intensity, amount of missing data, and the amount of noise in the valid data. Two criteria to check for GPOD convergence also were investigated. The MF method filled in the missing data with the lowest error across all parameters tested, with approximately one-third the computational cost of Kriging. Furthermore, the accuracy of MF GPOD was relatively insensitive to the quality of the convergence criterion. Therefore, compared to the three other GPOD methods and Kriging interpolation, the MF GPOD method is an effective method for filling missing data in PIV measurements in the studied gas turbine combustor flows.

1 Introduction

Gas turbine engines have found widespread use in powering aircraft, ships, tanks, and electrical generators. However, gas turbine combustors (GTC) remain a challenge to design due to the interaction of swirling, turbulent, multi-phase flow with the combustion chemistry, acoustics, walls, etc. Knowledge of the velocity field in a GTC can help elucidate such interactions, validate and improve computational fluid dynamics simulations, and aid in producing better designs. For instance, lean premixed combustors are susceptible to thermoacoustic instabilities, which can decrease efficiency, increase emissions, and eventually lead to structural damage (Huang and Yang 2009; Syred 2006). These instabilities arise from coupling between heat release, pressure, and flow oscillations, and so understanding the velocity field dynamics is important for determining coupling mechanisms. Other important GTC phenomena that are linked to the velocity field include blow-off, flashback, and ignition (Knole and Sattelmayaer 2009; Dhanuka et al. 2009; Littlejohn and Cheng 2007).

Accurate velocity field measurements are challenging in GTCs, particularly temporally resolved (i.e. multi-kHz repetition rate) measurements at practical operating conditions. Particle image velocimetry (PIV) is the de facto standard 2D velocity measurement technique in GTC-relevant flows (e.g. Fureby et al. 2007; Stopper et al. 2013; Temme et al. 2014; Arndt et al. 2015; Boxx et al. 2015; Cosic et al. 2015; Caux-Brisebois et al. 2014). However, multi-kHz PIV measurements from diode-pumped solid-state lasers typically generate relatively low signal compared to conventional pulsed lasers, while high-pressure liquid-fueled combustion generates high background luminosity from flame chemiluminescence and soot. Furthermore, achieving good PIV seed particle distribution can be challenging in high pressure GTC rigs due to the wide variety of gas densities and the complexity of the flow hardware. Localized regions therefore often exist in instantaneous measurements where low signal-to-noise or insufficient seed density results in gaps in the measured velocity field. Such gaps can cause issues with time series analysis, modal decomposition, or other data mining techniques requiring continuous data in either space or time.

Fig. 1

Comparison of the reconstructions of a missing vortex (blue vectors) calculated through Delaunay triangulation (spatial interpolation) and GPOD (spatio-temporal interpolation). The size of the data set from which this velocity field was taken is 200 snapshots. a Original field, b spatial interpolation, c GPOD reconstruction

One solution to this problem is to reconstruct the data that should occupy the gaps, wherein the accuracy of the reconstruction technique is key. This is demonstrated in Fig. 1, which shows a vortex (blue) and its reconstruction based on the remaining data (black) using various techniques. Figure 1b shows the vortex reconstructed using spatial interpolation through Delaunay triangulation, which fails to reconstruct the missing vortex. This is because it can only utilize data in a local region around the missing points for the reconstruction.

In comparison, spatiotemporal reconstruction techniques provide estimates for instantaneous gaps in the data using knowledge gained from the complete time series of measurements. Typical PIV data sets contain several hundred snapshots of the velocity field; this number can be in the thousands when measurements are performed at a multi-kHz repetition rate. Therefore, it is possible to use the large amount of data to obtain a better estimate for the missing data within the gaps than is possible just based on spatial interpolation. Gappy Proper Orthogonal Decomposition (GPOD) is a technique that works on this principle. GPOD was first used by Everson and Sirovich (1995) for facial recognition, and has since been applied to PIV (Gunes et al. 2006; Raben et al. 2012). As shown in Fig. 1c, the optimized GPOD described below provides an accurate reconstruction of the missing vortex.

Furthermore, reconstruction of missing data is necessary for accurate modal analysis. For example, conventional POD is commonly used to extract the energetic features of a flow. However, missing data corrupts such an analysis. This is demonstrated in Fig. 2, which shows the eigenvalue (energy) associated with the first 100 modes from a POD analysis applied to a set of gas turbine combustor velocity fields (described below), the same data but with 25 % gaps added, and the gappy data reconstructed using the MF GPOD method described in Sect. 2.2.4. As can be seen, the POD analysis with missing vectors deviates substantially from from the correct modal decomposition of the data, particularly in the lowest (most energetic) modes. In contrast, the modal analysis of the GPOD reconstructed data accurately matches the original data.

Fig. 2

Comparison of the first 100 eigenvalues calculated from the POD approximation of original vector fields (7870 snapshots), gappy fields (25 % mean gappiness), and fields reconstructed using GPOD

The objective of this paper is to assess and develop GPOD methods for reconstructing missing data in PIV measurements, particularly as pertaining to turbulent swirl flames typical of modern gas turbine combustors. Aspects of swirl flames that are interesting for GPOD include the highly 3D flow, thermoacoustically coupled flow oscillations, large recirculation zones, and coherent periodic flow structures such as precessing vortex cores (PVC). Four different GPOD methods are implemented in this paper, three adapted from literature and one novel method that utilizes ideas from PIV post-processing (Everson and Sirovich 1995; Gunes et al. 2006; Raben et al. 2012; Westerweel and Scarano 2005). Additionally, local Kriging, an advanced spatial interpolation technique, also was implemented and compared with the GPOD methods. The assessment is performed on high vector yield PIV data sets from an atmospheric pressure combustor, with artificial gaps added to them that mimic the low data yield typical of high pressure data. Experimental parameters considered include the gappiness of the velocity fields, the combustor conditions (specifically the turbulence intensity), and noise in the valid data.

2 Methodology

Before describing the GPOD methods employed in this work, a brief overview of POD is provided below.

2.1 Proper orthogonal decomposition

POD is a data analysis method that provides a low dimensional approximation to high-dimensional processes in the form of a linear combination of basis functions. The POD basis functions, also called eigenmodes, are calculated from the data directly, and therefore no a priori knowledge is required regarding the process that generates the data. The main feature of POD is that it provides the most efficient way of capturing dominant components in the data by constructing the approximation using only the most energetic modes (Liang et al. 2002).

POD is a well established technique. In this work, the method of snapshots described by Sirovich (1987) is used. Given a set of N measurements of the field $\xi (\mathbf {x},t)$, its POD approximation using P modes ($\breve{\xi }\large|_P$) is a linear combination of P temporal coefficients ($a_{i}$) and spatial modes ($\phi _{i}$)

$$\begin{aligned} \breve{\xi }(\mathbf {x},t_k)\large|_P = \sum _{i=1}^{P} a_{i}^k \phi _{i}(\mathbf {x}); \;\;\;\;\; k \in [1,N] \end{aligned}$$

(1)

Typically, the number of modes used for reconstruction is much fewer than the total number of snapshots of $\xi$ ($P \ll N$).

Using the method of snapshots, the spatial modes are defined as a linear combination of the temporal coefficients and the snapshots

$$\begin{aligned} \phi _{i}(\mathbf {x}) = \sum _{k=1}^{N} a_{i}^k \; \xi (\mathbf {x},t_k) \end{aligned}$$

(2)

The coefficients, $a_{i}$, can be found by solving for the eigenvectors of the correlation matrix $\mathbf {R}$

$$\begin{aligned} R_{ij} = \frac{\left( \; \xi (\mathbf {x},t_{i}), \; \xi (\mathbf {x},t_{j}) \; \right) }{N} \end{aligned}$$

(3)

$$\begin{aligned} \varvec{R} \varvec{a} = \varvec{\varLambda } \varvec{a} \end{aligned}$$

(4)

The eigenvalues of the correlation matrix, $\lambda _{i}$ (elements of the diagonal matrix $\varvec{\varLambda }$), correspond to the energy of the flow contained in mode i , and are ordered such that $\lambda _{n-1} > \lambda _{n}$.

Solving the eigenvalue problem on the complete data set is computationally expensive, and approximations typically are used. Here, a block-Lanczos method is used to approximate the singular value decomposition (SVD) of $\varvec{R}$ (Rokhlin et al. 2009). SVD is an extension of eigenvalue decomposition for non-square and non-symmetric matrices that can be used to get the necessary coefficients and eigenmodes for a POD analysis (Liang et al. 2002). One issue with POD is that any gaps in the data are treated as real information, and hence will influence the eigenmodes over the entire data set.

2.2 GPOD methods

GPOD is an extension of POD that provides high accuracy approximations for missing or erroneous data in measurements. The core of all GPOD techniques consists of an iterative implementation of POD on the incomplete data set. Instantaneous gaps in the data set are given an initial value, usually the point-wise mean over all the snapshots having good data at that point. This prevents the POD from attempting to produce zeros (gaps) at the locations and times of missing data. After each POD calculation, the guess for the data in the gaps is updated based on a POD approximation using a particular number of modes. The method/criteria by which the update is performed defines the GPOD method. This process is iterated until some convergence criterion is reached.

Before introducing the various GPOD methods, it is necessary to discuss the number of POD modes used in the reconstructions, P. As mentioned, all GPOD methods attempt to improve an initial guess at the missing data based on a P-mode POD. However, the optimal value of P is not known. A large number of modes with a poor initial guess for the missing data results in more details of that poor guess being reconstructed, whereas a small number of modes reduces the accuracy of reconstructing fine details. GPOD therefore typically is applied iteratively with an increasing number of modes, $P_{n}$ (Venturi and Karniadakis 2004). Starting with a simple initial guess and a low value of $P_0$, an improved approximation for the missing data from the converged GPOD calculation is passed as the initial guess for a calculation with $P_1>P_0$ modes, and so on. The number of modes is increased until a convergence criterion is reached. This iterative procedure has been shown to improve the accuracy of GPOD significantly (Venturi and Karniadakis 2004; Gunes et al. 2006).

This procedure results in a nested loop, with iterations both on the POD convergence with a given number of modes and the number of modes used. The former, described in Sect. 2.2.1, will hereafter be called sub-iterations, while the iterations of P will be called the main iterations. $P_0 = 2$ and $P_{n+1} = P_{n}+1$ is used in this work. Convergence criteria for both the sub- and main-iterations are discussed in Sect. 2.3. In what follows, $\mathbf {x}_{{\rm d}}|_{t_k}$ and $\mathbf {x}_\mathrm{g}|_{t_k}$ are the locations of valid data points and data gaps at $t_k$, respectively, n indexes the main iteration, and j indexes the sub-iterations.

Four GPOD methods were implemented in this paper. The two underlying methods are those introduced by Everson and Sirovich (1995) and Gunes et al. (2006). These are classified as non-adaptive methods, since the updated approximation for each gap location is accepted regardless of any metric. Two adaptive methods also are implemented, which utilize some form of outlier detection to accept or reject updates. Raben et al. (2012) utilized outlier detection based on field smoothness, which is implemented here along with a new method using median filtering. While the adaptive methods are more computationally intensive, they potentially can reduce the reconstruction error by allowing each missing data point to use the optimal number of modes in its approximation. Furthermore, GPOD is performed on each component of the velocity data $(u_x,u_y,u_z)$ separately, allowing independent convergence. Therefore, the final reconstructed field has velocity components that have been taken from iterations of GPOD that are not necessarily the same.

2.2.1 Everson Sirovich method

The Everson-Sirovich (ES) method was the first GPOD method to be introduced (Everson and Sirovich 1995). The procedure is as follows:

• 1. For a given main iteration (n), gaps in the original gappy field ($\xi$) are filled with an initial guess, resulting in a approximate filled field ($\bar{\xi }_{n,0}$). For $n = 0$, the guess at a given spatial point is based on the mean at that point, viz.

  $$\begin{aligned} {\bar{\xi }}_{0,0}(\mathbf {x},t_k) = {\left\{ \begin{array}{ll} \xi (\mathbf {x},t_k) & \mathbf {x}\in \mathbf {x}_\mathrm{d}|_{t_k}\\ \left<\xi (\mathbf {x})\right> & \mathbf {x}\in \mathbf {x}_\mathrm{g}|_{t_k} \end{array}\right. } \end{aligned}$$

  where $\left<\xi (\mathbf {x})\right>$ is the temporal mean of $\xi$ over all valid data at the location being evaluated. For $n>0$, $\bar{\xi }_{n,0}$ is the output from previous main iteration, i.e. $\bar{\xi }_{n,0} = \hat{\xi }_{n-1}$ (see Step 5).

• 2. POD analysis is performed on $\bar{\xi }_{n,j}$ using $P_{n}$ modes, resulting in a POD approximation

  $$\begin{aligned} \breve{\bar{\xi }}_{j}(\mathbf {x},t_k)\large|_{P_{n}} = \sum _{i=1}^{P_{n}} a_{i}^k \phi _{i}(\mathbf {x}) \end{aligned}$$

• 3. A second set of temporal coefficients ($b_{i}$) is calculated by minimizing the error between the known data and an approximation based on the POD spatial modes, i.e. minimizing

  $$\begin{aligned} \sum _{k = 1}^{N}\left\|\xi (\mathbf {x}_\mathrm{d}|_{t_k},t_k) - \tilde{\xi }_{n,j}(\mathbf {x}_{d}|_{t_k},t_k)\large|_{P_{n}} \right\|\end{aligned}$$

  where $\tilde{\xi }_{n,j}(\mathbf {x},t_k)\large|_{P_{n}} = \sum _{i=1}^{P_{n}} b_{i}^k \phi _{i}(\mathbf {x})$.

• 4. The gaps in the original data are filled using the POD-like reconstruction arising from the minimization problem

  $$\begin{aligned} \bar{\xi }_{n,j+1}(\mathbf {x},t_k) = {\left\{ \begin{array}{ll} \xi (\mathbf {x},t_k) & \mathbf {x} \in \mathbf {x}_\mathrm{d}|_{t_k}\\ \tilde{\xi }_{n,j}(\mathbf {x},t_k)\large|_{P_{n}} & \mathbf {x} \in \mathbf {x}_\mathrm{g}|_{t_k} \end{array}\right. } \end{aligned}$$

• 5. Steps (2–4) are repeated with $j = j+1$ until the POD eigenvalues calculated in step 2 converge within some preset tolerance, at which point the final approximation at main iteration n is stored as $\hat{\xi }_{n}$, and passed to the next main-iteration.

By solving the minimization problem, the ES method provides a high accuracy estimate during each sub-iteration. However, solving this minimization problem requires the inversion of large matrices, which increases the computational cost.

2.2.2 Gunes method

The method of Gunes et al. (2006) is similar to the ES method, but uses $a_{i}$ directly to estimate the gaps in the data, i.e. $\tilde{\xi } = \breve{\bar{\xi }}$. Since no minimization problem is solved to determine $b_{i}$, there is no need to invert large matrices and the Gunes method is more computationally efficient. This comes at the cost of decreased accuracy for a given value of P, but Gunes et al. (2006) and Raben et al. (2012) found this decrease to be small when both the methods were implemented in the iterative approach mentioned in the beginning of this section.

2.2.3 Field smoothness method

The field smoothness (FS) method implemented here is a slight modification of the adaptive reconstruction POD (AR-POD) method introduced by Raben et al. (2012). In both methods, an outlier detection method is employed between the main iterations to improve the accuracy of reconstructions by allowing individual points in the field to converge independently. That is, individual points are only updated with the new approximation value if that value is ‘better’ than the previous approximation, according to some metric. The FS method bases this metric on the field smoothness, which is defined at a point $\mathbf {x}_\mathrm{cp}$ in a 2D field as

$$\begin{aligned} F_{s}({\xi })|_{\mathbf {x}_\mathrm{cp},t_k} =\left. \frac{\partial ^2 \xi }{\partial x^2} \right| _{\mathbf {x}_\mathrm{cp},t_k}^2 + 2\left. \frac{\partial ^2 \xi }{\partial x \partial y} \right| _{\mathbf {x}_\mathrm{cp},t_k}^2 + \left. \frac{\partial ^2 \xi }{\partial y^2} \right| _{\mathbf {x}_\mathrm{cp},t_k}^2 \end{aligned}$$

(5)

Here, the FS method is run with a Gunes method core. That is,

• 1. Gunes method is run with $P_{n}$ modes on a field $\bar{\xi }_{n,0}$ to get an approximation $\hat{\xi }_{n}$.

• 2. For $n>0$, the field smoothness is calculated for the previous and current reconstructions, $F_{s,n-1} = F_s\left( \hat{\xi }_{n-1}\right)$ and $F_{s,n} = F_s\left( \hat{\xi }_{n}\right)$ respectively.

• 3. The input to the next main iteration is is updated such that

  $$\begin{aligned}&{\hat{\hat{\xi }}}_{n}({\mathbf {x},t_k}) = &{\left\{ \begin{array}{ll} {\hat{\xi }}_{n-1}({\mathbf {x}_\mathrm{cp},t_k}), &\quad \text {if }\, F_{s,n-1}|_{\mathbf {x}_\mathrm{cp},t_k} \le F_{s,n}|_{\mathbf {x}_\mathrm{cp},t_k}\\ {\hat{\xi }}_{n}({\mathbf {x}_\mathrm{cp},t_k}), &\quad \text {if}\, F_{s,n-1}|_{\mathbf {x}_\mathrm{cp},t_k} > F_{s,n}|_{\mathbf {x}_\mathrm{cp},t_k} \end{array}\right. } \end{aligned}$$

  (6)

  and $\bar{\xi }_{n+1,0} = {\hat{\hat{\xi }}}_{n}$.

• 4. Steps (1–3) are repeated with increasing modes ($n = n+1$) until the main iteration convergence criterion is reached.

The difference between the FS method and the AR-POD method is in the way ${\hat{\hat{\xi }}}_{n+1}$ is updated. Here, a single pass approach of the FS calculation is used, whereas AR-POD used a multi-pass iterative approach. Raben et al. (2012) found that the single-pass technique works better for cases in which missing data are grouped in clusters, which is typical for the type of noise experienced in gas turbine combustors.

2.2.4 Median filter method

Similar to the FS method, the median filter (MF) GPOD method introduced here makes use of an outlier detection technique between main iterations to adaptively select the best reconstruction at each point. However, the outlier detection metric in this case is based on a median filter, a common PIV outlier detection technique that has a high detection efficiency and is easy to implement (Raffel et al. 2007). The MF method requires calculation of the residual of $\xi$ at point $\mathbf {x}_\mathrm{cp}$ centered in a neighborhood of adjacent vectors ($\mathbf {x}_{c,ad}$):

$$\begin{aligned} R\left( \xi \right) |_{\mathbf {x}_\mathrm{cp},t_k} = \left| \xi (\mathbf {x}_\mathrm{cp},t_k) - \hbox {median}\left( \xi (\mathbf {x}_{c,ad},t_k) \right) \right| \end{aligned}$$

(7)

In this work, the neighbourhood size was kept at 9 (1 center vector and 8 adjacent vectors). This leads to the following procedure for the MF method:

• 1. Gunes method is run with $P_{n}$ modes on a field $\bar{\xi }_{n,0}$ to get an approximation $\hat{\xi }_{n}$.

• 2. For $n>0$, the median residual is calculated for the previous and current reconstructions: $R_{n-1} = R( \hat{\xi }_{n-1})$ and $R_{n} = R( \hat{\xi }_{n})$ respectively.

• 3. The input to the next main iteration is is updated such that

  $$\begin{aligned}&\hat{\hat{\xi }}_{n}({\mathbf {x},t_k}) = &{\left\{ \begin{array}{ll} {\hat{\xi }}_{n-1}(\mathbf {x}_\mathrm{cp},t_k), &\quad \text {if }\, R_{n-1}|_{\mathbf {x}_\mathrm{cp},t_k} \le R_{n}|_{\mathbf {x}_\mathrm{cp},t_k}\\ {\hat{\xi }}_{n}(\mathbf {x}_\mathrm{cp},t_k), &\quad \text {if }\, R_{n-1}|_{\mathbf {x}_\mathrm{cp},t_k} > R_{n}|_{\mathbf {x}_\mathrm{cp},t_k} \end{array}\right. } \end{aligned}$$

  (8)

  and ${\bar{\xi }}_{n+1,0} = {\hat{\hat{\xi }}}_{n}$.

• 4. Steps (1–3) are repeated with increasing modes ($n = n+1$) until the main iteration convergence criterion is reached.

It should be noted that the normalized median filter introduced by Westerweel and Scarano (2005), which allows a flow-independent threshold to determine whether a vector is an outlier, is not needed here. This is because the median filter is used to compare the residuals at the same point in two reconstructions of the same velocity field. Comparison is made between those two residuals, not between the residual and some threshold level, to determine whether to accept or reject a value.

2.3 Convergence criteria

2.3.1 Main iterations

A suitable convergence criterion for the main iterations is important, since the reconstruction error does not monotonically decrease with P (Venturi and Karniadakis 2004; Raben et al. 2012; Gunes et al. 2006). The reconstruction error using a particular number of modes is defined as

$$\begin{aligned} E(P_{n}) = \frac{1}{N} \sum _{k=1}^{N} \psi _{k}(P_{n}) \end{aligned}$$

(9)

$$\begin{aligned} \psi _{k}(P_{n}) = \frac{||\hat{\xi }_{n}(\mathbf {x}_\mathrm{g}|_{t_k}, t_k) - \xi (\mathbf {x}_\mathrm{g}|_{t_k}, t_k) ||}{||\xi (\mathbf {x}_\mathrm{g}|_{t_k}, t_k)||} \end{aligned}$$

(10)

where $||. ||$ is defined as

$$\begin{aligned} ||\mathbf {a} || = \sqrt{ \sum _{i=0}^{N} {a_{i}}^2 } \text { for } \mathbf {a} = \left\{ a_1,a_2,\ldots ,a_N \right\} \end{aligned}$$

(11)

This error is calculated only over the gaps in data; valid vectors are ignored. It is noted that calculation of this error requires knowledge of the true data that should exist in the gaps. Such information would not be available for real gappy data, but can be calculated here since the gaps have been artificially added to complete data sets. Hence, the reconstruction error is used here to evaluate different convergence criteria for the main iterations based on how well they capture the number of modes that minimizes E. This error equation is similar to the time averaged relative error used by Gunes et al. (2006).

Since E cannot be calculated for real gappy experimental data, different convergence criteria are needed for the main iterations; two of these criteria are tested here. The first was introduced by Gunes et al. (2006), and consists of adding additional convergence checking (CC) gaps to the already gappy data. The amount of these gaps is kept low, around 3 % of the data, to reduce their influence on the accuracy of the GPOD reconstruction of the real gaps. Since the CC gaps are artificial, the reconstruction error over these gaps can be calculated

$$\begin{aligned} E_\mathrm{cc}(P_{n}) = \frac{1}{N} \sum _{k=1}^{N} \psi _{cc,k}(P) \end{aligned}$$

(12)

$$\begin{aligned} \psi _{cc,k}(P_{n})= \frac{||\hat{\xi }_{n}(\mathbf {x}_\mathrm{cc}|_{t_k}, t_k) - \xi (\mathbf {x}_\mathrm{cc}|_{t_k}, t_k) ||}{||\xi (\mathbf {x}_\mathrm{cc}|_{t_k}, t_k)||} \end{aligned}$$

(13)

where $\mathbf {x}_\mathrm{cc}|_{t_k}$ are the locations of the CC gaps at $t_k$. Convergence is achieved when $E_\mathrm{cc}(P_{n})$ is minimized. Success of this technique depends on how well the CC gaps reflect the real gaps in the data, i.e. how well $E_\mathrm{cc}(P_{n})$ follows the behavior of $E(P_{n})$.

The second converge checking technique analyzes the kinetic energy (K) of the POD reconstruction, as expressed by the eigenvalues. Venturi and Karniadakis (2004) proposed that the optimal number of modes is such that

$$\begin{aligned}\left| K_{P_{n}} - K_{P_0} \right| \text { is a maximum, where } K_{P_{n}} = \sum _{i = 1}^{N}\lambda _{n,i}^2 \end{aligned}$$

(14)

Here, $K_{P_0}$ is the kinetic energy of the initial guess, before the GPOD procedure is started. It should be noted that these eigenvalues are calculated for all the modes (1..N), not just the $P_{n}$ modes used in the reconstruction.

2.3.2 Sub-iterations

Sub-iteration convergence is relatively simple, and is based on convergence of the eigenvalues associated with the POD calculation, $\lambda _{n,j,i}$, where the third index (i) indicates the POD mode associated with that eigenvalue. Specifically, convergence was based on

$$\begin{aligned} \frac{1}{P_{n}}\sum _{i = 1}^{P_{n}}\left| \frac{\lambda _{n,j,i}-\lambda _{n,j-1,i}}{\lambda _{n,j,i}}\right| < \varepsilon \end{aligned}$$

(15)

It is expected that a lower value of $\varepsilon$ will result in a lower reconstruction error. However, it was determined that $\varepsilon = 0.1$ produced the lowest error. This counterintuitive result is a product of the nested loop style iterative implementation of GPOD, i.e. the presence of the main iterations along with the sub-iterations. When a low value of $\varepsilon$ is chosen, the reconstructed field calculated at the end of each main iteration is the converged result arising from POD approximations of the initial guess. A good initial guess will yield an accurate reconstructed field, while a poor initial guess will yield a poorly reconstructed field. This is different from the case where a high value of $\varepsilon$ is chosen, wherein the resulting field is not fully converged, and as such is not very susceptible to the quality of the initial guess.

Keeping this in mind, the coupling effect of $\varepsilon$ and the number of modes used for the main iterations can be determined. Since the main iterations begin with a small number of modes ($P_0 = 2$), the initial fields for the first few iterations have a poor initial guess as the number of modes used in the POD approximation is not enough to capture most of the important features in the flow. Therefore, choosing a small value of $\varepsilon$ in such a case will result in a poorly reconstructed field for a given main iteration, which is then passed on to the next iteration and so forth. It should be noted that simply starting with a high number of modes ($P_0 \gg 2$) is not a viable solution since the initial guess of the first main iteration is the time averaged field, and so reconstructing from it using high number of modes will result in the capturing of poor data by the POD approximation.

Conversely, if a high value of $\varepsilon$ is chosen, the reconstructed fields of the initial main iterations are not affected severely by the poor initial guess as before, and as such there is less error propagating from the first few main iterations. However, when the number of modes increases to a number high enough to capture important features in the flow, the use of a large $\varepsilon$ will result in less accurate reconstructions as the fields from the sub-iterations have not converged yet. In such a case, a small value of $\varepsilon$ works better. Therefore, in order to achieve a low reconstruction error, an optimal $\varepsilon$ needs to be chosen that works well for low and high number of modes.

The previously mentioned value of $\varepsilon = 0.1$ was determined here by running some of the data sets with varying levels of $\varepsilon$ and comparing the reconstruction error. To apply this to cases with ‘real’ gappy data, the previously mentioned CC gaps will be needed in order to monitor the reconstruction error.

2.4 GPOD testing procedure

The capabilities of GPOD for swirl flames is assessed in this work by artificially adding gaps to high quality PIV data, implementing the various GPOD methods and convergence criteria on those gappy fields, and then comparing the reconstructions to the original non-gappy fields based on the total reconstruction error (Eq. 10). These high quality data sets, which are described in Sect. 3, have essentially no missing vectors and therefore are appropriate for this type of assessment.

The main parameter that was considered when adding gaps to the data was the percentage of missing vectors, or the gappiness percentage (G). This parameter is defined as the ratio of the number of missing vectors to the total number of possible vector points, and was set to 5, 15, 25, and 50 %. It is noted that the cases with 50 % missing data are intended to stress the limitations of the techniques; the utility of data sets with this degree of missing data would need to be evaluated on a case-by-case basis. In order to realistically mimic the distribution of gaps in time, the total number of missing vectors was distributed in a Gaussian manner across snapshots, with the mean of this distribution being set to the aforementioned percentages. The gaps were added such that no single snapshot had all the data missing and no single point in the field was missing for all snapshots, as all GPOD methods breakdown unless these criteria are met.

2.5 Kriging interpolation

In addition to GPOD, Kriging also was evaluated. Kriging is an advanced spatial interpolation technique that was first used in the field of geology (Oliver and Webster 1990); its application has since been extended to PIV measurements (Gunes et al. 2006; Raben et al. 2012). For small data sets, i.e. ones with few snapshots or velocity fields, Kriging interpolation was shown by Gunes et al. (2006) to produce more accurate reconstructions than GPOD. However, they found the opposite to be true for large PIV data sets. Raben et al. (2012) found Kriging to be more accurate than their AR-POD method when working with artificially gappy experimental data (similar to the analysis in the current work). It is therefore worthwhile to compare the performance of GPOD methods to that of Kriging.

In Kriging interpolation, a surface function is created using available points in a grid. This function is then interpolated at the query points (gaps) to get an estimate at those points. This interpolation also makes use of weight functions, which can be calculated using variograms, covariograms, or correlograms; the current work makes uses correlograms. The weight function is chosen such that it minimizes the variance of the estimator function. Similar to GPOD, Kriging interpolation here is run on one velocity component at a time. In this work, Kriging interpolation was implemented in MATLAB using the DACE toolbox, and a more in depth mathematical description of the technique can be found in Lophaven et al. (2002). The exponential correlation model was chosen over the Gaussian one, as the former was found to give lower reconstruction errors than the latter.

3 Experimental data

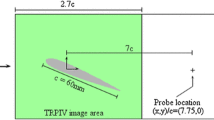
The capabilities of GPOD for GTCs were tested on high vector yield PIV data taken from turbulent swirl flames in an atmospheric pressure gas turbine model combustor having an 85 mm × 85 mm × 114 mm combustion chamber and a measured swirl number of 0.55. The combustor has been the subject of numerous previous studies (e.g. Meier et al. 2007; Franzelli et al. 2012; Dem et al. 2015; Oberleithner et al. 2015) wherein the geometry is discussed in detail, and the data used here were previously described by Steinberg et al. (2013) and Caux-Brisebois et al. (2014). To summarize, 10 kHz stereoscopic PIV (S-PIV) vector fields were computed using the LaVision DaVis 8.0 software package, with a final interrogation box size and vector spacing of approximately 1.0 and 0.5 mm respectively, and a total number of 7870 snapshots per data set. The field-of-view imaged by the PIV system was approximately 49 mm × 38 mm. Due to optical access restrictions caused by the combustion chamber posts, the S-PIV field-of-view was offset from the centerline of the burner, covering the range $x = -17$ to 32 mm. Furthermore, reflections from the windows caused increased measurement noise at some locations for $x<0$. Since the analysis performed here required high-quality data, only measurements at $x>0$ were used.

Four perfectly premixed methane/air flames were analyzed, which are summarized in Table 1. These cases had increasing flow rate, and hence increasing turbulence. The turbulence level was characterized by the turbulent kinetic energy (q), as measured by the PIV at the center of the swirling inflow jet and 1.5 mm downstream of the combustor dump plane. The downstream location was selected to avoid noise caused by laser sheet reflections. The jet center, defined as the peak velocity in a radial slice, occurred at approximately $r = 11$ mm.

It was previously mentioned that these data sets were chosen due to their high vector yield, which allows for the comparison of reconstructed vectors to original ones at all locations of artificial gaps. The implicit assumption here is that the vectors in the data sets have little uncertainty. However, it is not possible to get PIV data that is completely free from noise, and so it is important to quantify the uncertainty in the calculated vectors. Here, this was accomplished using an a posteriori uncertainty quantification technique implemented in the LaVision DaVis 8.3.0 software package; details of this technique can be found in Wieneke (2015). Presented in last column of Table 1 is the average relative uncertainty in the vector magnitude, averaged over space and time for each case.

Table 1 List of experimental cases showing the turbulence level (q), air and fuel flow rates ($\dot{m}_A$ and $\dot{m}_{\mathrm{CH}_4}$, respectively), the thermal power ($P_\mathrm{th}$), and an estimate of the average uncertainty in the calculated vectors

4 Results and discussion

GPOD evaluation was performed in two stages. Firstly, the minimum absolute error (E) produced by the different GPOD methods was compared. This is the minimum error that could be achieved if the main-iteration convergence criterion perfectly predicted the optimal number of POD modes to use in the reconstruction. Hence, it is the fundamental evaluation of the capabilities of the different GPOD methods. Secondly, the influence of main iteration convergence criterion was evaluated, i.e. how well the different convergence metrics identify the minimum absolute error.

Before beginning the evaluation, it is worthwhile to illustrate the vector fields produced at the different stages of the GPOD process. A non-gappy vector field at an arbitrary time in a measurement sequence from Case 1 is shown in Fig. 3a, while the same field with $G=50\,\%$ data gaps added is shown in Fig. 3b. The initial guess to the filled field, $\bar{\xi }_{0,0}$, is shown in Fig. 3c, where the filled values are based on the temporal mean over non-missing data at each location. The MF GPOD method is then applied onto this field. An intermediate solution after the $P = 10$ main-iteration ($\hat{\hat{\xi }}_{10}$) is shown in Fig. 3d, in which a better correspondence with the target field can be seen. This field is then passed to the next main iteration. The final vector field that corresponds to the minimum value of E, i.e. the optimally reconstructed field, is shown in Fig. 3e. This field closely resembles the real target vector field and qualitatively shows the capabilities of GPOD as a reconstruction technique. Quantitatively, the reconstruction error (Eq. 10) for this particular field is 0.18 and 0.15 for the $u_x$ and $u_y$ velocity components, respectively. Figure 3f shows the reconstructed field acquired using the kinetic energy convergence check. There is very little visible difference between this field and the previous one that was reconstructed using the optimal number of modes. Further analysis of the convergence checking techniques is provided in Sect. 4.2.

Fig. 3

Part of an instantaneous velocity field ($G=50\,\%$) for Case 1 at various stages in the GPOD process for the MF method. Shown in the background is the relative error, $\left| \frac{\hat{\xi }_{n}(\mathbf {x}_\mathrm{g}) - \xi (\mathbf {x}_\mathrm{g}) }{\xi (\mathbf {x}_\mathrm{g})} \right|$, at each vector. Axes are in millimeters. a Original field, b gappy field, c initial guess (time averaged values), d GPOD reconstructed field after 10 main iterations, e GPOD reconstructed field stopped at the optimal number of modes, f GPOD reconstructed field stopped at modes with maximum K

4.1 Error comparison

Having shown, qualitatively, the accuracy of GPOD reconstructions, a quantitative comparison of the four GPOD methods and Kriging interpolation is now presented. Shown in Fig. 4 are the error curves for the three velocity components in Case 4, with $G = 25\,\%$. It is noted that Case 4 was at the highest velocity and had the highest reconstruction error of all cases at a given G. The curves for all three components exhibit the same trend; as $P_{n}$ increases, the error initially decreases, reaches a minimum ($E^*$), and then begins to monotonically increase. However, the error minima occur at different modes ($P^*$) for each velocity component and for each method. The former indicates that GPOD must be performed on each velocity component independently in order to minimize the total error. The minimum reconstruction error is similar for $u_x$ and $u_y$, but is higher for $u_z$. This likely is a result of higher uncertainty in the $u_z$ measurement that is inherent to S-PIV, which adds randomness to the data that cannot be predicted by GPOD.

Fig. 4

Error curves of the four GPOD methods for Case 4, with mean $G=25\,\%$. Black dots are at the point corresponding to the error minima ($E^* = E({P^*})$) of the corresponding curves. The curves have been truncated after the minima. a u _x , b u _y , c u _z

The error curves in Fig. 4 are nearly identical for the ES and Gunes methods, which is in agreement with Raben et al. (2012) and Gunes et al. (2006). Even though the ES method solves a minimization problem and has a higher computational cost, there is no substantive gain in accuracy over the Gunes method for the data studied here. This is most likely a result of their iterative implementation with respect to the number of modes. Hence, only results from the Gunes method will be reported below. The adaptive methods result in considerably less error than the non-adaptive methods, with the $E^*_\mathrm{FS}$ and $E^*_\mathrm{MF}$ being around 21 and 38 % (relative difference) less than $E^*_\mathrm{Gunes}$, respectively. Both adaptive methods are more accurate than the non-adaptive methods for all values of P, and the MF method is more accurate than the FS method before $P^*_\mathrm{FS}$ is reached. Kriging interpolation is more accurate than the FS method, which agrees with the findings of Raben et al. (2012), but the MF method has a minimum reconstruction error that is lower by about 5 % (relative difference). Overall, the MF method is quantitatively the most accurate reconstruction technique.

Although Kriging interpolation results in reconstructions that are only slightly less accurate than those of the MF method, it is less favourable as it takes more time to reconstruct the entire data set. For instance, for Case 4 run with 25 % mean gappiness, the amount of time required for the MF method to reach $P^*$ for a single velocity component was roughly one-third the time it took Kriging interpolation to reconstruct the same component. Both reconstruction techniques were processed using MATLAB 2014b running on a desktop workstation with an Intel(R) Core(TM) i5-2400 CPU and 16 GB of RAM.

Fig. 5

Root mean squared of the minimum error values, $E^*$, of all three velocity components ($u_x,u_y,u_z$) as a function of mean gappiness percentage, turbulence intensity, and noise. a Effect of gappiness percentage (Case 4). b Effect of turbulence intensity ($G = 25\,\%$). c Effect of noise (Case 1 with $G = 25\,\%$)

Figure 5a shows $E^*$ for the different GPOD methods and Kriging interpolation at the three different gappiness percentages for Case 4. All four methods have the same general trend of increasing error with increasing G. For the GPOD methods, this is because increased gappiness results in less real information passed to the POD, and consequently less accurate GPOD reconstructions. Increased gappiness also means that there are fewer valid data points for Kriging interpolation. The MF method is the most accurate at all values of G, followed by Kriging, the FS method, and the Gunes method. It should be noted that even for sparsely gappy case ($G = 5\,\%$), where one can expect local interpolation to work well, the MF method is still more accurate than Kriging.

Figure 5b presents $E^*$ for varying levels of turbulence, i.e. across the four cases from Table 1. The reconstruction error increases monotonically with turbulence intensity, which is expected since the flow features increasingly random stochastic fluctuations with increasing turbulence. In all cases, the MF method was the most accurate.

It was mentioned previously that the data being used here is not necessarily devoid of noise, which can affect the accuracy of the GPOD reconstructions. In order to gauge this effect, varying levels of Gaussian noise were added to the valid data of Case 1 with 25 % gappiness. The resulting minimum reconstruction errors of the four GPOD methods and Kriging interpolation are presented in Fig. 5c. The noise was added using the randn function in MATLAB, which provides a Gaussian distribution of random noise ranging from 0 to 1: $\xi _\mathrm{noise} = \xi + \alpha \, {randn}(0,1)$. In the figure, the normalized noise coefficient is defined as $\alpha/V_{\mathrm{mag},\mathrm{bulk}}$, where $V_{\mathrm{mag},\mathrm{bulk}}$ is the mean velocity magnitude measured by the PIV at the center of the swirling inflow jet and 1.5 mm downstream of the combustor dump plane. The curves show that increasing noise in the data increases the reconstruction error, which is to be expected. It appears that, compared to the GPOD methods, the accuracy of Kriging interpolation is more susceptible to noise. This is most likely due to Kriging’s reliance only on local spatial information, as opposed to the global spatio-temporal information utilized by GPOD.

While the reconstruction error is a useful metric, it is a single metric for the error and may mask some important features. It therefore is worthwhile to understand how this number arises in the actual data. This will be demonstrated for Case 4 using the MF method with $G = 25$ %, for which $E^*=0.33$. The error is mostly affected by the small vectors. Shown in Fig. 6 are the conditional PDFs of the relative error over all the gaps the data set for different ranges of the absolute velocity of the $u_x$ component. For small velocities (less than 5 m/s), the relative error can be quite large as a result of the small denominator. On the other hand, the relative error over the larger vectors is much lower. This is evident in the error contours of Fig. 3 as well. Using the uncertainty quantification method mentioned in Sect. 3, the mean relative uncertainty for vectors in the range of $|u_x| \in (0,5]$ m/s was calculated to be 67 %, while the same number was only 2.5 and 1.1 % for velocity ranges of $|u_x| \in (5,10]$ m/s and $|u_x| \in (10,\infty)$ m/s, respectively. This indicates that the lower velocities in the PIV measurements are possibly noisier, which is most likely the reason why their reconstruction errors are higher. Therefore, the overall reconstruction error is largely controlled by locations with low velocities.

Fig. 6

PDFs of the relative error, $\left| \frac{\hat{\xi }_{n}(\mathbf {x}_\mathrm{g}) - \xi (\mathbf {x}_\mathrm{g}) }{\xi (\mathbf {x}_\mathrm{g})} \right|$, in the MF GPOD reconstructed $u_x$ component conditioned on $|u_x|$. Case 4 with $G = 25$ %

4.2 Convergence criteria for real gappy data

The analysis above demonstrates the potential of GPOD to accurately represent missing data from PIV measurements. However, the methods are limited in practice by the ability to stop the GPOD calculation at the optimal number of modes. It is noted that, for the adaptive methods, each missing data point has its own optimal number of modes since the approximation is only updated if the new value satisfies the criteria described in Sect. 2.2. Hence, the E versus P curves in Fig. 4 do not increase as rapidly at $P>P^*$ for the FS and MF methods as for the ES and Gunes methods.

Nevertheless, a robust and accurate method for determining when to stop the GPOD main iterations is necessary both for accuracy and computational efficiency. Hence, the two convergence criteria described in Sect. 2.3 were tested. For brevity, results are presented below for the Gunes method (non-adaptive) and MF method (adaptive); the ES and FS results agreed with these findings.

Fig. 7

Curves of E for varying levels of convergence checking gaps. Both the Gunes and MF method were run on Case 4 at 25 % gappiness of the ‘real’ gaps. Only $u_x$ has been shown. Black dots represent minima of E while white dots represent locations of the minima of $E_c$. a Gunes method, b MF method

Figure 7 shows E versus P curves from the convergence criterion based on adding convergence checking gaps. Case 4 with $G = 25\,\%$ is used as exemplary data. GPOD was run with different percentages of CC gaps ($G_\mathrm{cc}$) in order to evaluate the effect of removing more data on the overall accuracy and convergence. It should be noted that E is calculated only over the ‘real’ gaps, and not the CC gaps. Points are marked on the curves that correspond to $E^*$ at $P^*$ (black dots) and the minimum over just the CC gaps ($E^*_\mathrm{cc}$, white dots), which occurs at $P^*_\mathrm{cc}$.

In all cases, $E^*_\mathrm{cc}>E^*$ and $P^*_\mathrm{cc}>P^*$. Hence, GPOD would run for a larger number of modes than necessary and result in a higher overall error. For the Gunes method, for which E rapidly increases for $P>P^*$, the discrepancy between the real error minimum and that predicted by the CC gaps generally decreased as $G_\mathrm{cc}$ increased towards G, since the convergence checking gaps become a better representation of the actual missing data. However, the absolute error also increased since less data is used in the GPOD reconstruction. Nevertheless, the decrease in $P^*_{CC}$ outweighed the increased total error for the Gunes method.

The performance of the CC gap convergence criterion for the MF method is not the same as for the Gunes method. As shown in Fig. 7b, there is not a monotonic decrease in the spacing between $P^*_\mathrm{cc}$ and $P^*$ as $G_\mathrm{cc}$ was increased. However, because the adaptive nature of the MF method results in relatively flat E curves in the vicinity of $P^*$, over prediction of $P^*$ does not significantly affect the final error. For example, $E^*_\mathrm{cc} \approx 1.2E^*$ for the Gunes method with $G_\mathrm{cc} = 3\,\%$, but $E^*_\mathrm{cc} \approx 1.0005E^*$ for the MF method, even though $P^*_\mathrm{cc}$ exceeds $P^*$ by a similar amount for both methods. In the MF method, the decreased accuracy associated with increased $G_{CC}$ outweighs any decreases in $P^*_{CC}$. Hence, the use of a low percentage of CC gaps is an appropriate convergence check for the MF method.

Fig. 8

Plots of error curves of Gunes and MF methods run for Case 4 at 25 % gappiness. Black dots are minima of E and red dots are the location of the maximum K

The second convergence checking method requires the calculation of the turbulent kinetic energy (K) from the POD analysis at each main iteration. Figure 8 shows E curves of the Gunes and MF methods run for Case 4 at 25 % gappiness. Black dots represent the minima of the curves whereas the red dots are locations of the maxima of K ($P_K^*$) for each method. For the Gunes method, $P_K^*$ is much closer to $P^*$ than any of the $P_\mathrm{cc}^*$ values from Fig. 7a. Since there is no need to add CC gaps for this convergence method, the error E will not be increased due to the extra missing data. This makes using turbulent kinetic energy a good measure of convergence when using the Gunes method. On the other hand, this technique over-predicts the location of the error minimum for the MF method, as $P_K^*$ is larger than $P^*$ by 246 iterations. However, since the error curves of the MF method are relatively flat near $P^*$, the increase in error is insignificant ($E^*_K \approx 1.005 E^*$). This is also evidenced by the minor differences between Fig. 3e, f. Therefore, either convergence checking method can be used. It should be noted that since the TKE method requires the calculation of all the POD eigenvalues for the data set at each main iteration, its computation time is higher than the CC gaps convergence check.

5 Conclusion

This paper evaluated the use of gappy proper orthogonal decomposition as a method of filling in missing data that may occur in gas turbine combustor particle image velocimetry measurements. In addition to three previously described GPOD methods, a new adaptive methodology was developed that uses a local median filter to decide whether to update the GPOD approximation at a given location after each main iteration. These methods were also compared to Kriging interpolation, an advanced local spatial interpolation technique. The different GPOD methods were tested on high-quality S-PIV data obtained in an atmospheric pressure swirl flame, into which artificial gaps were added. A range of turbulence intensities and amounts of missing data (gappiness percentage) were investigated, as well as two methods of checking convergence.

The newly implemented MF method resulted in lower error than the previous GPOD methods and Kriging interpolation across all conditions and gappiness percentages. The final reconstruction error increased monotonically with both the gappiness, turbulence intensity, and artificial noise in the data. However, good reconstructions could be obtained, even with 50 % missing data.

The use of artificial gaps to check for convergence was found to over predict the optimal number of modes that minimized the error in the reconstructions. This was particularly problematic for non-adaptive methods, for which the error increased rapidly as the number of modes increased. However, the MF method had a relatively flat error curve around the minimum error, and the over prediction of modes did not significantly affect the final reconstruction error. Increasing the amount of the convergence checking gaps decreased the over prediction of the optimal number of modes, but also increased the overall error since less data was used in the GPOD.

The use of the kinetic energy calculated from POD analysis for convergence also was evaluated. This technique does not require adding additional gaps, so the reconstruction error can be reduced. This method also over predicted the optimal number of modes. For the non-adaptive GPOD method, the kinetic energy provided a better prediction of the optimal number of modes. For the adaptive MF method, it provided a poorer prediction. However, the poor prediction for the MF method did not significantly affect the final error due to the relative flatness of the error curve.

As part of future studies on this topic, the capabilities of GPOD should be tested against cases with systematic gappiness, as opposed to the random gappiness studied here. These cases, which can arise from a fluttering shear layer, for instance, will contain certain regions in the flow-field that are more susceptible to gaps, and so it is possible that the reconstruction at those locations would be effected significantly. In terms of improving the GPOD methods, it would be worth looking into a combination of Kriging and GPOD. In this work, GPOD is run iteratively (with respect to the main iterations), which was shown by Venturi and Karniadakis (2004) to be insensitive to the initial guess. It is possible that a non-iterative implementation of GPOD that utilizes a good initial guess, e.g. fields reconstructed using Kriging, could yield better reconstructions than the iterative GPOD.