Comparison of Gaussian and super Gaussian laser beams for addressing atomic qubits

Abstract

We study the fidelity of single-qubit quantum gates performed with two-frequency laser fields that have a Gaussian or super Gaussian spatial mode. Numerical simulations are used to account for imperfections arising from atomic motion in an optical trap, spatially varying Stark shifts of the trapping and control beams, and transverse and axial misalignment of the control beams. Numerical results that account for the three-dimensional distribution of control light show that a super Gaussian mode with intensity $I\sim \hbox {e}^{-2(r/w_0)^n}$ provides reduced sensitivity to atomic motion and beam misalignment. Choosing a super Gaussian with $n=6$ the decay time of finite temperature Rabi oscillations can be increased by a factor of 60 compared to an $n=2$ Gaussian beam, while reducing crosstalk to neighboring qubit sites.

Appendix 1: On-resonance Rabi frequency and differential AC Stark shift for two-photon Raman transitions via \(7^2P_{1/2}\) in \(^{133}\)Cs including hyperfine splitting

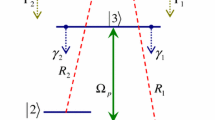
The Rabi oscillations investigated in this work are driven via a Raman process from the $F=3, m_F=0$ hyperfine ground state of the $6^2S_{1/2}$ manifold in $^{133}$Cs to its $F=4,m_F=0$ hyperfine ground state via the $7^2P_{1/2}$ manifold using two laser beams. To treat this kind of Rabi oscillation, we repeat the steps from Sect. 2.4 for a $\varLambda$-type three-level system with two lasers tuned to the two transitions of the Raman process. For detunings large enough so that the excited-state population is small, we can adiabatically eliminate the $7^2P_{1/2}$ state, resulting in an effective two-level Rabi oscillation with an on-resonance Rabi frequency of

$$\begin{aligned} \varOmega =\frac{\varOmega _1 \varOmega _2^*}{2 \varDelta _R}, \end{aligned}$$

(20)

where $\varOmega _{1,2}$ are the single-photon on-resonance Rabi frequencies for the $6^2S_{1/2}, F=3, m_F=0 \rightarrow 7^2P_{1/2}$ and $7^2P_{1/2} \rightarrow 6^2S_{1/2}, F=4, m_F=0$ transitions, respectively. $\varDelta _R$ is the detuning of the first Raman laser beam from the $6^2S_{1/2}, F=3 \rightarrow 7^2P_{1/2}$ (fine structure level) transition, and we have assumed that the detuning of the second Raman laser from the $6^2S_{1/2}, F=4 \rightarrow 7^2P_{1/2}$ transition is the same. Equation (20) is valid for two-photon resonance or when the departure from two-photon resonance is small compared to $\varDelta _R$.

Taking into account the hyperfine splitting of the $7^2P_{1/2}$ level, we have to sum over all possible intermediate states, resulting in

$$\begin{aligned} \varOmega =\sum _{F'}\frac{\varOmega _{1,F_1 F'} \varOmega _{2,F' F_2}^*}{2 \varDelta _{R,F'}}, \end{aligned}$$

where $F', F_{1,2}$ are the total angular momentum quantum numbers of the intermediate, initial, and final states, respectively, $\varOmega _{1,F_1 F'}$ and $\varOmega _{2,F' F_2}$ are the single-photon on-resonance Rabi frequencies for the $F_1 \rightarrow F'$ and $F' \rightarrow F_2$ transitions, respectively, and $\varDelta _{R,F'}$ is the detuning of the first Raman laser beam from the $F_1 \rightarrow F'$ transition.

In $^{133}$Cs, we have $F_1=3$, $F_2=4$, and $F'=3,4$. We thus find for the two-photon on-resonance Rabi frequency

$$\begin{aligned} \varOmega =\frac{\varOmega _{1,33'} \varOmega _{2,3'4}^*}{2 \varDelta _{R,3'}}+\frac{\varOmega _{1,34'} \varOmega _{2,4'4}^*}{2 \varDelta _{R,4'}}, \end{aligned}$$

where we used primes to indicate quantum numbers pertaining to the excited states. The detunings from the $7^2P_{1/2}$ hyperfine states are $\varDelta _{R,3'}=\varDelta _R-\varDelta _{F'3}$ and $\varDelta _{R,4'}=\varDelta _R-\varDelta _{F'4}$. Here, $\varDelta _{F'3}=-2\pi \times 212.3\,\text {MHz}$ and $\varDelta _{F'4}=2\pi \times 165.1\,\text {MHz}$ are the hyperfine shifts from the $7^2P_{1/2}$ fine structure level to the $F'=3,4$ hyperfine states, respectively.

The one-photon Rabi frequencies are $\varOmega _{i,F_i F_f}=\varOmega _{i,0} \tilde{\varOmega }_{F_i F_f}$ with $\varOmega _{i,0}= {\mathcal {E}}_i e \langle 7^2P_{1/2}||r||6^2S_{1/2}\rangle /\hbar$, where ${\mathcal {E}}_i$ is the electric field amplitude of Raman laser $i=1,2$, $e\langle 7^2P_{1/2}||r||6^2S_{1/2}\rangle$ is the reduced dipole matrix element for the $6^2S_{1/2} \rightarrow 7^2P_{1/2}$ transition, e is the elementary charge, and

$$\begin{aligned} \tilde{\varOmega }_{F_1 F'}=c_{J_1,I,F_1}^{J',I,F'}C_{F_1,m_{F1},1,q_1}^{F',m_{F1}+q_1} \end{aligned}$$

for a Raman absorption and

$$\begin{aligned} \tilde{\varOmega }_{F' F_2}=c_{J',I,F'}^{J_1,I,F_2}C_{F',m_{F1}+q_1,1,-q_2}^{F_2,m_{F1}+q_1-q_2} \end{aligned}$$

for a stimulated Raman emission. Here, $C_{F_1,m_{F1},1,q_1}^{F',m_{F1}+q_1}$ and $C_{F',m_{F1}+q_1,1,-q_2}^{F_2,m_{F1}+q_1-q_2}$ are Clebsch–Gordan coefficients, and

$$\begin{aligned} c_{J_1,I,F_i}^{J',I,F_j}=(-1)^{1+I+F_i+J'}\sqrt{2F_i+1}\left\{ \begin{array}{ccc} J_1 &{} I &{} F_i \\ F_j &{} 1 &{} J' \end{array}\right\} . \end{aligned}$$

For our specific transitions in $^{133}$Cs, $6^2S_{1/2}, F=3, m_F=0 \rightarrow 7^2P_{1/2}, F=3,4, m_F=1$ and $7^2P_{1/2}, F=3,4, m_F=1 \rightarrow 6^2S_{1/2}, F=4, m_F=0$, the relevant quantum numbers are the initial and final total electron angular momentum quantum numbers $J_1=J'=1/2$, the nuclear spin quantum number $I=7/2$, the initial magnetic quantum number $m_{F1}=0$, and we use circularly polarized Raman laser beams such that the z-components of the angular momentum of the absorbed and emitted photons are $q_1=q_2=1$. With these, we find

$$\begin{aligned} \tilde{\varOmega }_{33'}&= {} c_{1/2,7/2,3}^{1/2,7/2,3}C_{3,0,1,1}^{3,1}=1/4, \\ \tilde{\varOmega }_{3'4}&= {} c_{1/2,7/2,3}^{1/2,7/2,4}C_{3,1,1,-1}^{4,0}=1/4, \\ \tilde{\varOmega }_{34'}&= {} c_{1/2,7/2,3}^{1/2,7/2,4}C_{3,0,1,1}^{4,1}=\sqrt{5/48}, \\ \tilde{\varOmega }_{4'4}&= {} c_{1/2,7/2,4}^{1/2,7/2,4}C_{4,1,1,-1}^{4,0}=\sqrt{5/48}. \end{aligned}$$

The reduced dipole matrix element for the $6^2S_{1/2}\rightarrow 7^2P_{1/2}$ transition in $^{133}$Cs is $e\langle 7^2P_{1/2}||r||6^2S_{1/2}\rangle =0.276 ea_0$ [19], where $a_0$ is the Bohr radius.

Altogether, we find the two-photon on-resonance Rabi frequency to be

$$\begin{aligned} \varOmega =\frac{\varOmega _{1,0}\varOmega _{2,0}^*}{32}\left( \frac{1}{ \varDelta _R-\varDelta _{F'3}}+\frac{5/3}{\varDelta _R-\varDelta _{F'4}}\right) . \end{aligned}$$

To find the total Stark shift of each of the hyperfine ground states, we need to add the Stark shifts due to the first and second Raman laser beams, so

$$\begin{aligned} \varDelta _{\mathrm{ac},F}=\varDelta _{\mathrm{ac},F, R1}+\varDelta _{\mathrm{ac},F, R2} \end{aligned}$$

(21)

For each hyperfine ground state, we must sum over the contributions due to each of the hyperfine states of the $7^2P_{1/2}$ manifold, resulting in

$$\begin{aligned} \varDelta _{\mathrm{ac},F, R1/R2}=\sum _{F'}\frac{|\varOmega _{F F'}|^2}{4\varDelta _{R,F'}}. \end{aligned}$$

Thus, the AC Stark shift of the $F=3$ hyperfine ground state due to the first Raman laser is

$$\begin{aligned} \varDelta _{\mathrm{ac},3, \mathrm{R}1}&= {} \frac{|\varOmega _{1,33'}|^2}{4\varDelta _{R,3'}} +\frac{|\varOmega _{1,34'}|^2}{4\varDelta _{R,4'}} \\&= {} \frac{|\varOmega _{1,0}|^2}{64}\left( \frac{1}{\varDelta _R-\varDelta _{F'3}}+ \frac{5/3}{\varDelta _R-\varDelta _{F'4}}\right) . \end{aligned}$$

Similarly, the contribution to the AC Stark shift due to the second Raman laser is

$$\begin{aligned} \varDelta _{\mathrm{ac},3, \mathrm{R}2}&= {} \frac{|\varOmega _{2,33'}|^2}{4\left( \varDelta _{R,3'}-\varDelta _{hf}\right) }+ \frac{|\varOmega _{2,34'}|^2}{4\left( \varDelta _{R,4'}-\varDelta _{hf}\right) } \\ &= {} \frac{|\varOmega _{2,0}|^2}{64}\left( \frac{1}{\varDelta _R-\varDelta _{F'3}-\varDelta _{hf}}+ \frac{5/3}{\varDelta _R-\varDelta _{F'4}-\varDelta _{hf}}\right) , \end{aligned}$$

where $\varDelta _{hf}=2\pi \times 9.192631770$ GHz is the ground-state hyperfine splitting of $^{133}$Cs.

The contribution of the first Raman laser to the AC Stark shift of the $F=4$ hyperfine ground state is

$$\begin{aligned} \varDelta _{\mathrm{ac},4, \mathrm{R}1}&= {} \frac{|\varOmega _{1,43'}|^2}{4\left( \varDelta _{R,3'}+\varDelta _{hf}\right) }+ \frac{|\varOmega _{1,44'}|^2}{4\left( \varDelta _{R,4'}+\varDelta _{hf}\right) } \\ &= {} \frac{|\varOmega _{1,0}|^2}{64}\left( \frac{1}{\varDelta _R-\varDelta _{F'3}+\varDelta _{hf}}+ \frac{5/3}{\varDelta _R-\varDelta _{F'4}+\varDelta _{hf}}\right) . \end{aligned}$$

Here, we have used

$$\begin{aligned} \tilde{\varOmega }_{43'}=c_{1/2,7/2,4}^{1/2,7/2,3}C_{4,0,1,1}^{3,1}=-1/4. \end{aligned}$$

and

$$\begin{aligned} \tilde{\varOmega }_{44'}=c_{1/2,7/2,4}^{1/2,7/2,4}C_{4,0,1,1}^{4,1}=-\sqrt{5/48}. \end{aligned}$$

Finally, the contribution of the second Raman laser beam to the AC Stark shift of the $F=4$ ground state is

$$\begin{aligned} \varDelta _{\mathrm{ac},4, \mathrm{R}2}&= {} \frac{|\varOmega _{2,43'}|^2}{4\left( \varDelta _{R,3'}\right) }+ \frac{|\varOmega _{2,44'}|^2}{4\left( \varDelta _{R,4'}\right) } \\ &= {} \frac{|\varOmega _{2,0}|^2}{64}\left( \frac{1}{\varDelta _R-\varDelta _{F'3}}+ \frac{5/3}{\varDelta _R-\varDelta _{F'4}}\right) . \end{aligned}$$

The differential Stark shift between the $F=3$ and $F=4$ hyperfine ground states is

$$\begin{aligned} \varDelta _{\mathrm{ac}R}=\varDelta _{\mathrm{ac},4}-\varDelta _{\mathrm{ac},3}. \end{aligned}$$

In this work, we used two Raman laser beams of identical power, waist, and alignment, so ${\mathcal {E}}_1={\mathcal {E}}_2$, and consequently

$$\begin{aligned} \varDelta _{\mathrm{ac}R} &= {} \frac{|\varOmega _{1,0}|^2}{64} \left( \frac{1}{\varDelta _R-\varDelta _{F'3}+\varDelta _{hf}} +\frac{5/3}{\varDelta _R-\varDelta _{F'4}+\varDelta _{hf}}\right. \\ & \quad -\left. \frac{1}{\varDelta _R-\varDelta _{F'3}-\varDelta _{hf}}- \frac{5/3}{\varDelta _R-\varDelta _{F'4}-\varDelta _{hf}}\right) . \end{aligned}$$