Appendices
A Newtonian flow produced by the translation and radial expansion of a sphere
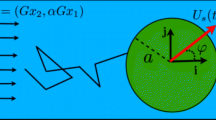
Here we derive the velocity field \(\mathbf {u} (\mathbf {x})\) of a LRN flow produced by a sphere of radius R, pulled by a force \(\mathbf {F}\) and expanding radially at a rate \(\dot{R} = \text {d} R / \text {d} t\). Due to the linearity of LRN flows, the velocity field is the sum of two terms: that resulting from the drag force—\(\mathbf {u} \{ \mathbf {F} \}\), and that resulting from the radial expansion—\(\mathbf {u} \{ \dot{R} \}\) :
$$\begin{aligned} \mathbf {u} = \mathbf {u} \{ \mathbf {F} \} + \mathbf {u} \{ \dot{R} \} \end{aligned}$$
(A.1)
The flow produced by the translation of a solid sphere is a classical result (Pozrikidis 1992). It can be represented in terms of a Stokeslet and dipole with poles at the center of the sphere that are given by
$$\begin{aligned} \mathbf {G}= & {} \dfrac{\mathbf {\mathbf {I}}}{r} + \dfrac{\mathbf {r}\mathbf {r}}{r^3} \end{aligned}$$
(A.2)
$$\begin{aligned} {\mathbf D}= & {} -\dfrac{\mathbf {I}}{ r^3} + 3\dfrac{\mathbf {r}\mathbf {r}}{r^5} \end{aligned}$$
(A.3)
where \(\mathbf {x}_0\) is the center of the sphere, \(\mathbf {r} = \mathbf {x} - \mathbf {x}_0\) and \(r = | \mathbf {r} |\). \(\mathbf G\) is called the Oseen tensor. The velocity field is then
$$\begin{aligned} u_i (\mathbf {x}) = G_{ij} (\mathbf {x}, \mathbf {x}_0) \Big ( \dfrac{3}{4} R U_j \Big ) - D_{ij} (\mathbf {x}, \mathbf {x}_0) \Big ( \dfrac{1}{4} R^3 U_j \Big ). \end{aligned}$$
(A.4)
Here \(\mathbf {U}\) is the translational velocity of the sphere, i.e., \(\mathbf {U} (t) = \dot{\mathbf {x}}_0 (t)\). The relation between the drag force \(\mathbf {F}\) and \(\mathbf {U}\) is
$$\begin{aligned} \mathbf {F} = 6 \pi \mu R \mathbf {U} \end{aligned}$$
(A.5)
Using the above one obtains the fluid velocity
$$\begin{aligned} u_i= & {} \dfrac{1}{24 \pi \mu } \Big [ 3 \Big ( \dfrac{\delta _{ij}}{r} + \dfrac{r_i r_j}{r^3} \Big ) F_j - \Big ( - \dfrac{\delta _{ij}}{r^3} + 3 \dfrac{r_i r_j}{r^5} \Big ) R^2 F_j \Big ] \\= & {} \dfrac{1}{24 \pi \mu } \Big [ 3 \Big ( \dfrac{F_i}{r} + \dfrac{(\mathbf {F} \cdot \mathbf {r}) r_i}{r^3} \Big ) + \Big ( \dfrac{F_i}{r^3} - 3 \dfrac{(\mathbf {F} \cdot \mathbf {r}) r_i}{r^5} \Big ) R^2\Big ] \\= & {} \dfrac{1}{24 \pi \mu r} \Big [ \Big ( 3 + \dfrac{R^2}{r^2} \Big ) F_i + 3 (\dfrac{1}{r^2} - \dfrac{R^2}{r^4}) (\mathbf {F} \cdot \mathbf {r}) r_i \Big ] \end{aligned}$$
or alternatively
$$\begin{aligned} \mathbf {u} \{ \mathbf {F} \} = \dfrac{1}{24 \pi \mu r} \Big [ \Big ( 3 + \dfrac{R^2}{r^2} \Big ) \mathbf {F} + 3 \Big (1 - \dfrac{R^2}{r^2} \Big ) (\mathbf {F} \cdot \hat{\mathbf {r}}) \hat{\mathbf {r}} \Big ] \end{aligned}$$
(A.6)
where \(\hat{\mathbf {r}} = \mathbf {r} / |\mathbf {r}|\).
The velocity field \(\mathbf {u} \{ \dot{R} \}\) of the flow produced by a radially expanding sphere can be represented by a point source with pole at the center \(\mathbf {x}_0\) of the sphere, and thus has the form
$$\begin{aligned} \mathbf {u} = \alpha \dfrac{ \hat{\mathbf {r}}}{r^2} \end{aligned}$$
(A.7)
where the strength of the source (\(\alpha \)) is a constant to be determined. The no-slip boundary condition on the sphere surface implies that
$$\begin{aligned} \mathbf {u} (\mathbf {x}) = \dfrac{\text {d} R}{\text {d} t} \hat{\mathbf {r}}. \end{aligned}$$
(A.8)
From (A.7, A.8) we find that \(\alpha = \dot{R} R^2\), and therefore
$$\begin{aligned} \mathbf {u} \{ \dot{R} \} = \dot{R} \Big ( \dfrac{R}{r} \Big )^2 \hat{\mathbf {r}}. \end{aligned}$$
(A.9)
If we represent it in terms of the sphere volume \(v = 4 \pi R^3 /3\) this reads
$$\begin{aligned} \mathbf {u} \{ \dot{R} \} = \dfrac{\dot{v}}{4 \pi r^2} \hat{\mathbf {r}} \end{aligned}$$
(A.10)
This leads to the combined flow Eq. (3.16):
$$\begin{aligned} \mathbf {u} \big ( \mathbf {r}; R, \mathbf {F}, \dot{R} \big ) = \dfrac{1}{24 \pi \mu r} \Big [ \big ( 3 + \dfrac{R^2}{r^2} \big ) \mathbf {F} + 3 \big ( 1 - \dfrac{R^2}{r^2} \big ) \big ( \mathbf {F} \cdot \widehat{ \mathbf {r} } \big ) \widehat{\mathbf {r}} \Big ] +\dot{R} \Big ( \dfrac{R}{r} \Big )^2 \widehat{\mathbf {r}}. \end{aligned}$$
B Accuracy of \(U_i^{(e)}\) after incorporating the second reflection
Next we determine how a second reflection contributes to the rigid motions of two radially expanding spheres.
0th reflection We consider two spheres with radii \(R_1 (t)\) and \(R_2 (t)\) resp., centered at \(\mathbf {x}_1 (t)\) and \(\mathbf {x}_2 (t)\) so that \(\mathbf {x}_2 - \mathbf {x}_1\) points in the \(\mathbf {e}_x\) direction. The radial expansion of the \(i\hbox {th}\) sphere alone generates a flow
$$\begin{aligned} \mathbf {u}_i^{(0)} ( \mathbf {x}) = R_i^2 \dot{R}_i \dfrac{\mathbf {x} - \mathbf {x}_i}{ | \mathbf {x} - \mathbf {x}_i |^3} \end{aligned}$$
(B.1)
and the rigid motion of the sphere vanishes
$$\begin{aligned} \mathbf {U}_i^{(0)} = \mathbf {0}, \quad \mathbf {\omega }_i^{(0)} = \mathbf {0}. \end{aligned}$$
(B.2)
1st Reflection. Next we put sphere 1 into the flow \(\mathbf {u}_2\) generated by the radially expanding sphere 2. We calculate the resulting translational velocity \(\mathbf {U}_1^{(1)}\), angular velocity \(\mathbf {\omega }_1^{(1)}\), and the stresslet \(\mathbf {S}_1^{(1)}\), from which we obtain the velocity field \(\mathbf {u}_{21} (\mathbf {x})\).
Translational velocity \(\mathbf {U}_1^{(1)}\).
$$\begin{aligned} \mathbf {U}_1^{(1)}= & {} \Big ( 1 + \dfrac{R_1^2}{6} \nabla ^2 \Big ) \mathbf {u}_2^{(0)} \Big |_{\mathbf {x} = \mathbf {x}_1} = R_2^2 \dot{R}_2 \Big [ \dfrac{\mathbf {x}_1 - \mathbf {x}_2}{ | \mathbf {x}_1 - \mathbf {x}_2 |^3} + \dfrac{R_1^2}{6} \nabla ^2 \Big ( \dfrac{\mathbf {x} - \mathbf {x}_2}{ | \mathbf {x} - \mathbf {x}_2 |^3} \Big ) \Big |_{\mathbf {x} = \mathbf {x}_1} \Big ] \\= & {} R_2^2 \dot{R}_2 \Big [ - \dfrac{ \mathbf {e}_z }{ l^2} + \dfrac{R_1^2}{6} \nabla ^2 \Big ( \dfrac{\mathbf {x} - \mathbf {x}_2}{ | \mathbf {x} - \mathbf {x}_2 |^3} \Big ) \Big |_{\mathbf {x} = \mathbf {x}_1} \Big ] \end{aligned}$$
Letting \(\mathbf {r} = \mathbf {x} - \mathbf {x}_2 \) and \(r = |\mathbf {r}|\), we must calculate
$$\begin{aligned} \nabla ^2 \Big ( \dfrac{\mathbf {r}}{r^3} \Big ) = \partial _k \partial _k \dfrac{r_i}{r^3} \end{aligned}$$
Since
$$\begin{aligned} \partial _k \Big ( \dfrac{1}{r^n} \Big ) = - \dfrac{n r_k}{r^{n+2}} \end{aligned}$$
we have
$$\begin{aligned} \partial _k \Big ( \dfrac{r_i}{r^3} \Big )= & {} \dfrac{\delta _{ik}}{r^3} - \dfrac{3 r_i r_k}{r^5} \\ \partial _k \partial _k \Big ( \dfrac{r_i}{r^3} \Big )= & {} - \dfrac{3 \delta _{ik} r_k}{r^5} - \dfrac{3 \delta _{ik} r_k}{r^5} - \dfrac{3 r_i \partial _k r_k}{r^5} + \dfrac{15 r_i r_k r_k}{r^7} = 0. \end{aligned}$$
Thus
$$\begin{aligned} \nabla ^2 \Big ( \dfrac{\mathbf {r}}{r^3} \Big ) = \mathbf {0} \end{aligned}$$
and
$$\begin{aligned} \mathbf {U}_1^{(1)} = - \dfrac{R_2^2 \dot{R}_2}{l^2} \mathbf {e}_x \end{aligned}$$
(B.3)
Angular velocity \(\mathbf {\omega }_1^{(1)}\).
$$\begin{aligned} \mathbf {\omega }_1^{(1)} = \dfrac{1}{2} \nabla \times \mathbf {u}_2^{(0)} \Big |_{\mathbf {x} = \mathbf {x}_1} = \mathbf {0} \end{aligned}$$
(B.4)
Stresslet \(\mathbf {S}_1^{(1)}\). The rate of deformation that results from \(\mathbf {u}_2\) is
$$\begin{aligned} \mathbf {E}_2^{(0)}= & {} \dfrac{1}{2} \Big [ \nabla \mathbf {u}_2^{(0)} + \big ( \nabla \mathbf {u}_2^{(0)} \big )^T \Big ] - \dfrac{1}{3} \mathbf {I} \Big ( \nabla \cdot \mathbf {u}_2^{(0)} \Big ) \\= & {} \dot{R}_2 R_2^2 \Big [ \dfrac{1}{2} \Big ( \nabla \dfrac{\hat{\mathbf {r}}}{r^2} + \big ( \nabla \dfrac{\hat{\mathbf {r}}}{r^2} \big )^T \Big ) - \dfrac{1}{3} \mathbf {I} \Big ( \nabla \cdot \dfrac{\hat{\mathbf {r}}}{r^2} \Big ) \Big ] \end{aligned}$$
where \(\hat{\mathbf {r}} = \mathbf {r}/r\). Using spherical coordinates, we have
$$\begin{aligned} \nabla \dfrac{\hat{\mathbf {r}}}{r^2}= & {} \Big ( \hat{\mathbf {r}} \dfrac{\partial }{\partial r} + \dfrac{1}{r} \hat{\mathbf {\theta }} \dfrac{\partial }{\partial \theta } + \dfrac{1}{r \sin \theta } \hat{\mathbf {\phi }} \dfrac{\partial }{\partial \phi } \Big ) \Big ( \dfrac{\hat{\mathbf {r}}}{r^2} \Big ) = \Big ( \dfrac{\partial }{\partial r} \dfrac{1}{r^2} \Big ) \hat{\mathbf {r}} \hat{\mathbf {r}} = - \dfrac{2}{r^3} \hat{\mathbf {r}} \hat{\mathbf {r}} \\ \nabla \cdot \dfrac{\hat{\mathbf {r}}}{r^2}= & {} \dfrac{\partial }{\partial r} \dfrac{1}{r^2} + \dfrac{2}{r} \dfrac{1}{r^2} = 0. \end{aligned}$$
Thus
$$\begin{aligned} \mathbf {E}_2^{(0)} = - \dfrac{2 R_2^2 \dot{R}_2}{r^3} \hat{\mathbf {r}} \hat{\mathbf {r}} = - \dfrac{2 R_2^2 \dot{R}_2}{r^5} \mathbf {r} \mathbf {r}, \end{aligned}$$
(B.5)
and the stresslet is given by
$$\begin{aligned} \mathbf {S}_1^{(1)}= & {} \dfrac{20}{3} \pi \mu R_1^3 \Big ( 1 + \dfrac{R_1^2}{10} \nabla ^2 \Big ) \mathbf {E}_2^{(0)} \Big |_{\mathbf {x} = \mathbf {x}_1} \\= & {} - \dfrac{40}{3} \pi \mu R_1^3 R_2^2 \dot{R}_2 \Big [ \dfrac{\mathbf {e}_x \mathbf {e}_x}{l^3} + \dfrac{R_1^2}{10} \nabla ^2 \Big ( \dfrac{\mathbf {r} \mathbf {r}}{r^5} \Big ) \Big |_{\mathbf {x} = \mathbf {x}_1} \Big ] \end{aligned}$$
We need to calculate
$$\begin{aligned} \nabla ^2 \Big ( \dfrac{\mathbf {r} \mathbf {r}}{r^5} \Big )= & {} \partial _k \partial _k \Big ( \dfrac{ r_i r_j }{r^5} \Big )\\ \partial _k \Big ( \dfrac{ r_i r_j }{r^5} \Big )= & {} \dfrac{\delta _{ik} r_j}{r^5} + \dfrac{\delta _{jk} r_i}{r^5} - \dfrac{5 r_i r_j r_k}{r^7} \\ \partial _k \partial _k \Big ( \dfrac{ r_i r_j }{r^5} \Big )= & {} \Big ( \dfrac{\delta _{ik} \delta _{jk}}{r^5} - \dfrac{5 \delta _{ik} r_j r_k}{r^7} \Big ) + \Big ( \dfrac{\delta _{jk} \delta _{ik}}{r^5} - \dfrac{5 \delta _{jk} r_i r_k}{r^7} \Big ) \\&+ \,\Big ( - \dfrac{5 \delta _{ik} r_j r_k}{r^7} - \dfrac{5 \delta _{jk} r_i r_k}{r^7} - \dfrac{5 r_i r_j \partial _k r_k}{r^7} + \dfrac{35 r_i r_j r_k r_k}{r^9} \Big ) = \dfrac{2 \delta _{ij}}{r^5} \end{aligned}$$
Thus
$$\begin{aligned} \mathbf {S}_1^{(1)} = - \dfrac{40}{3} \pi \mu R_1^3 R_2^2 \dot{R}_2 \Big [ \dfrac{\mathbf {e}_x \mathbf {e}_x}{l^3} + \dfrac{R_1^2}{5 l^5} \mathbf {I} \Big ] \end{aligned}$$
(B.6)
Finally, the velocity field \(\mathbf {u}_{21}^{(1)} (\mathbf {x})\) is given by
$$\begin{aligned} \mathbf {u}_{21}^{(1)} (\mathbf {x}) = \Big ( \mathbf {S}_1^{(1)} \cdot \nabla \Big ) \cdot \dfrac{\mathbf {G}(\mathbf {x} - \mathbf {x_1})}{8 \pi \mu } + \cdots \end{aligned}$$
(B.7)
From Eqs. (B.6, A.2) we have that near \(\mathbf {x}_1\),
$$\begin{aligned} \mathbf {S}_1^{(1)} \sim O \Big ( \dfrac{1}{l^3} \Big ), \quad \mathbf {G} \sim O \Big ( \dfrac{1}{l} \Big ) \end{aligned}$$
and thus the velocity near \(\mathbf {x}_1\) scales as \(\mathbf {u}_{21}^{(1)} \sim O (l^{-5})\).
2nd Reflection. Now we reflect once again and consider sphere 1 immersed in the flow \(\mathbf {u}_{12}^{(1)}\). The translational velocity \(\mathbf {U}_1^{(2)}\) that results is given by
$$\begin{aligned} \mathbf {U}_1^{(2)} = \Big ( 1 + \dfrac{R_1^2}{6} \nabla ^2 \Big ) \mathbf {u}_{12}^{(1)} \Big |_{\mathbf {x} = \mathbf {x}_1} \end{aligned}$$
(B.8)
From the discussion of the first reflection we know that near \(\mathbf {x}_1\) the velocity field \(\mathbf {u}_{12}^{(1)}\) is \(O (l^{-5})\), and thus \(\mathbf {U}_1^{(2)} \sim O (l^{-5})\) as well.
C Extended analysis and computation of a PMPY of small separation.
1.1 C.1 Results with the second reflection involved and accurate up to \(O (\delta ^5)\).
From Sect. 3.2, the translational velocities of the spheres after two reflections can be approximated as:
$$\begin{aligned} U_1= & {} \dfrac{F_1}{6 \pi \mu R_1} \Big ( 1 - \dfrac{15R_1 R_2^3}{4 l^4} \Big ) + \dfrac{F_2}{4 \pi \mu l} \Big ( 1 - \dfrac{R_1^2 + R_2^2}{3 l^2} \Big ) - \dot{R}_2 \Big ( \dfrac{R_2}{l} \Big )^2 + O \big ( \dfrac{1}{l^5} \big ) \\ U_2= & {} \dfrac{F_2}{6 \pi \mu R_2} \Big ( 1 - \dfrac{15R_1^3 R_2}{4 l^4} \Big ) + \dfrac{F_1}{4 \pi \mu l} \Big ( 1 - \dfrac{R_1^2 + R_2^2}{3 l^2} \Big ) + \dot{R}_1 \Big ( \dfrac{R_1}{l} \Big )^2 + O \big ( \dfrac{1}{l^5} \big ) \end{aligned}$$
After non-dimensionalization, they read:
$$\begin{aligned} U_1= & {} \dfrac{F_1}{R_1} \Big ( 1 - \dfrac{15R_1 R_2^3}{4 l^4} \delta ^4 \Big ) + \dfrac{3 F_2}{2l} \delta \Big ( 1 - \dfrac{R_1^2 + R_2^2}{3 l^2} \delta ^2 \Big ) - \delta ^2 \Big ( \dfrac{R_2}{l} \Big )^2 \zeta _2 + O (\delta ^5) \\ U_2= & {} \dfrac{F_2}{R_2} \Big ( 1 - \dfrac{15R_1^3 R_2}{4 l^4} \delta ^4 \Big ) + \dfrac{3 F_1}{2l} \delta \Big ( 1 - \dfrac{R_1^2 + R_2^2}{3 l^2} \delta ^2 \Big ) + \delta ^2 \Big ( \dfrac{R_1}{l} \Big )^2 \zeta _1 + O (\delta ^5) \end{aligned}$$
and the coefficient matrix in the system Eq. (3.24) becomes
$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} \alpha _1 &{} \varGamma \\ 0 &{} -1 &{} \varGamma &{} \alpha _2 \\ 1 &{} -1 &{} 0 &{} 0 \\ 0&{} 0&{} 1 &{} 1 \end{array}\right) \end{aligned}$$
(B.1)
where
$$\begin{aligned} \alpha _1= & {} \dfrac{1}{R_1} \Big ( 1 - \dfrac{15R_1 R_2^3}{4 l^4} \delta ^4 \Big ),\\ \alpha _2= & {} \dfrac{1}{R_2} \Big ( 1 - \dfrac{15R_1^3 R_2}{4 l^4} \delta ^4 \Big ),\\ \varGamma= & {} \delta \dfrac{3}{2l} \Big ( 1 - \dfrac{R_1^2 + R_2^2}{3 l^2} \delta ^2 \Big ) \end{aligned}$$
We consider the stroke in Eq. (3.35) again, but with solution obtained with the first reflection [Eq. (3.24), Fig. 4 black dots] or with both the first and the leading order term from second reflections [Eq. (3.24) with coefficient matrix in Eq. (B.1), Fig. 4 green crosses]—the former is truncated from the \(\delta ^4\) term while the latter is from the \(\delta ^5\) term. For small separation of the PMPY with \(l_0 = 7, \ \delta = 0.54\), simulation of the scaled translation and power are shown in Fig. 4, from which we see them match well. For this system, the first reflection is correct to \(O (\delta ^4)\) where \(\delta ^4 \sim 8.5E-2\), while with the leading order term from the second reflection included, it is correct to \(O (\delta ^5)\) where \(\delta ^5 \sim 4.6E-2\). However, in the simulation, the difference between the net translation after one cycle (X(1)) obtained by the two approximations is:
$$\begin{aligned} | X_{\text {1stRef}} (1) - X_{\text {2ndRef}} (1) | \sim 8.9 E-3 \end{aligned}$$
When comparing with \(\delta \), this difference gives the estimation of
$$\begin{aligned} | X_{\text {1stRef}} (1) - X_{\text {2ndRef}} (1) | \sim \delta ^{7.7} \end{aligned}$$
This implies that with \(\delta \) as large as 0.54, the solution obtained from the first reflection is accurate to the order of \(O (10^{-3})\) which approximates \(O (\delta ^{7.7})\).
1.2 C.2 Comparing the contributions of \(P_D\) and \(P_V\) to the power P.
As is discussed in Sect. 3.3, the power expended to propel a PMPY consists of two parts: \(P_D\) that results from the drag force on the spheres, and \(P_V\) that results from the radial expansion of the spheres. In addition, Eq. (3.31) shows that the higher-order corrections to P only exists in \(P_D\). We repeat the simulations in Fig. 3 with different values of \(l_0\) and show the results for \(P_D\) and \(P_V\) in Fig. 17, where \(P_D\) and \(P_V\) calculated by the first reflection are shown by green and blue solid lines, resp., and \(P_D\) calculated by Avron’s asymptotic approximation is shown by black dots.
D Calculation of \({\varvec{\varOmega }}_{3,i}^{(1)}\)
The angular velocity of sphere 3 (i.e., the free-floating sphere) \( {\varvec{\varOmega }}_{3,i}^{(1)}\) consists of two parts: \( {\varvec{\varOmega }}_{3,i}^{(1,f)}\) that results from the drag force on sphere i, and \( {\varvec{\varOmega }}_{3,i}^{(1,e)}\) that results from the expansion of sphere i. Here we calculate them separately.
First, \( {\varvec{\varOmega }}_{3,i}^{(1,e)}\), which results from the flow generated by the expansion of sphere i is:
$$\begin{aligned} \mathbf {u}_i^{(0,e)} = R_i^2 \dot{R}_i \dfrac{\mathbf {x} - \mathbf {x}_i}{|\mathbf {x} - \mathbf {x}_i|^3}, \end{aligned}$$
and therefore
$$\begin{aligned} {\varvec{\varOmega }}_{3,i}^{(1,e)} = \dfrac{1}{2} \nabla \times \mathbf {u}_i^{(e)} \Big |_{\mathbf {x} = \mathbf {x}_3} = \dfrac{ R_i^2 \dot{R}_i }{2} \nabla \times \Big ( \dfrac{\mathbf {x} - \mathbf {x}_i}{|\mathbf {x} - \mathbf {x}_i|^3} \Big ) \Big |_{\mathbf {x} = \mathbf {x}_3}. \end{aligned}$$
(D.1)
Let \(\mathbf {r} = \mathbf {x} - \mathbf {x}_i\) and \(r = |\mathbf {x} - \mathbf {x}_i| \), then the antisymmetric part in Eq. (D.1) is
$$\begin{aligned} \partial _j \Big ( \dfrac{r_k}{r^3} \Big ) - \partial _k \Big ( \dfrac{r_j}{r^3} \Big ) = \Big ( \dfrac{\delta _{jk}}{r^3} - \dfrac{3 r_j r_k}{r^5} \Big ) - \Big ( \dfrac{\delta _{kj}}{r^3} - \dfrac{3 r_k r_j}{r^5} \Big ) = 0 \end{aligned}$$
and therefore \( {\varvec{\varOmega }}_{3,i}^{(1,e)} = 0\).
Next, \( {\varvec{\varOmega }}_{3,i}^{(1,f)}\), which results from the flow generated by the drag force \(\mathbf {F}_i = F_i \mathbf {e}_x\) on sphere i, is given by
$$\begin{aligned} {\varvec{\varOmega }}_{3,i}^{(1,f)}= & {} \dfrac{1}{2} \nabla \times \mathbf {u} \{ \mathbf {F}_i \} \Big |_{\mathbf {x} = \mathbf {x}_3} \\= & {} \dfrac{1}{16 \pi \mu } \nabla \times \Big [ \Big ( \dfrac{1}{r} + \dfrac{1}{3 r^3} \Big )F_i \mathbf {e}_x + \Big ( \dfrac{1}{r} - \dfrac{1}{ r^3} \Big ) (F_i \mathbf {e}_x \cdot \dfrac{\mathbf {r}}{r}) \dfrac{\mathbf {r}}{r} \Big ] \Big |_{\mathbf {x} = \mathbf {x}_3} \\= & {} \dfrac{F_i}{16 \pi \mu } \nabla \times \Big [ \Big ( \dfrac{1}{r} + \dfrac{1}{3 r^3} \Big ) \mathbf {e}_x + \Big ( \dfrac{1}{r} - \dfrac{1}{ r^3} \Big ) \dfrac{r_x \mathbf {r}}{r^2} \Big ]. \end{aligned}$$
Since
$$\begin{aligned} \nabla \times \Big ( \dfrac{1}{r^n} \mathbf {e}_x \Big )= & {} - \dfrac{n r_z}{r^{n+2}} \mathbf {e}_y + \dfrac{n r_y}{r^{n+2}} \mathbf {e}_z \\ \nabla \times \Big (\dfrac{r_x}{r^n} \mathbf {r} \Big )= & {} - \dfrac{r_z}{r^n} \mathbf {e}_y + \dfrac{r_y}{r^n} \mathbf {e}_z \end{aligned}$$
we have
$$\begin{aligned} {\varvec{\varOmega }}_{3,i}^{(1,f)} = \dfrac{F_i}{8 \pi \mu r^3} \Big [ - r_z \mathbf {e}_y + r_y \mathbf {e}_z \Big ] \Big |_{\mathbf {r} = \mathbf {x}_3 - \mathbf {x}_i} = \dfrac{F_i}{8 \pi \mu l_{i3}^3} \big ( \mathbf {x}_3 - \mathbf {x}_i \big )_y \mathbf {e}_z \end{aligned}$$
(D.2)
and therefore
$$\begin{aligned} {\varvec{\varOmega }}_3^{(1)} = \sum _{i=1,2} {\varvec{\varOmega }}_{3,i}^{(1,f)} + {\varvec{\varOmega }}_{3,i}^{(1,e)} = \sum _{i=1,2} \dfrac{F_i}{8 \pi \mu l_{i3}^3} \big ( \mathbf {x}_3 - \mathbf {x}_i \big )_y \mathbf {e}_z. \end{aligned}$$
(D.3)
E Numerical scheme of two PMPY models
The following numerical scheme is written in terms of unscaled variables.
When the two PMPY models both lie along the x-axis, and the spheres are numbered 1, 2, 3, 4 from the negative to the positive x-direction, the Eqs. (5.1–5.9) reduce to
$$\begin{aligned} \left( \begin{array}{l@{\quad }l} A_{11} &{} A_{12} \\ A_{21} &{} A_{22} \end{array} \right) \left( \begin{array}{l} \mathbf {U} \\ \mathbf {F} \end{array} \right) = \left( \begin{array}{l} \mathbf {B}_1 \\ \mathbf {B}_2 \end{array} \right) \end{aligned}$$
(E.1)
where
$$\begin{aligned} \mathbf {U} = \left( \begin{array}{l} U_1\\ U_2\\ U_3\\ U_4 \end{array} \right) , \quad \mathbf {F} = \mu ^{-1} \left( \begin{array}{l} F_1\\ F_2\\ F_3\\ F_4 \end{array}\right) . \end{aligned}$$
Here \(A_{11} = - I_4\), where \(I_4\) is the \(4 \times 4\) identity matrix, \(A_{12} = (a_{ij})\) is a symmetric \(4 \times 4\) matrix, with
$$\begin{aligned} a_{ii} = \dfrac{1}{6 \pi R_i} , \quad a_{ij} = \dfrac{1}{4 \pi l_{ij}} \Big ( 1 - \dfrac{R_i^2 + R_j^2}{3 l_{ij}^2} \Big ) \end{aligned}$$
(E.2)
and
$$\begin{aligned} \big ( A_{21} \ A_{22} \big ) = \left( \begin{array}{r@{\quad }r@{\quad }r@{\quad }r@{\quad }r@{\quad }r@{\quad }r@{\quad }r} 1 &{} -1 &{} 0 &{} 0&{} 0 &{} 0&{} 0&{} 0 \\ 0&{} 0&{} 1 &{} -1 &{} 0 &{} 0&{} 0&{} 0 \\ 0 &{} 0&{} 0&{} 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0&{} 0&{} 0 &{} 0 &{} 0&{} 1 &{} 1 \end{array} \right) . \end{aligned}$$
\(\mathbf {B}_1 \in \mathbb {R}^4\), is given by
$$\begin{aligned} (\mathbf {B}_1)_i = - \sum _{j \ne i} \text {sign} (i-j) \dot{R}_j \Big ( \dfrac{R_j}{l_{ij}} \Big )^2 \end{aligned}$$
and
$$\begin{aligned} \mathbf {B}_2 = \left( \begin{array}{l} - \dot{l}_{12} \\ - \dot{l}_{34} \\ 0\\ 0 \end{array} \right) . \end{aligned}$$
With the second reflection considered, the leading term in \(\mathbf {U}_i^{(2)}\) is of order \(\delta ^4\), which results from the drag forces and can be computed from the following equations:
$$\begin{aligned} \mathbf {U}_i^{(2,f)} = \Big ( 1 + \dfrac{R_i^2}{6} \Big ) \nabla ^2 \sum _{j,k}^{k \ne i,j} \mathbf {u}_{jk}^{(1)} \Big |_{\mathbf {x} = \mathbf {x}_i} \end{aligned}$$
where
$$\begin{aligned} \mathbf {u}_{jk}^{(1)} = \big ( \mathbf {S}_{k,j}^{(1)} \cdot \nabla \big ) \cdot \dfrac{\mathbf {G} ( \mathbf {x} - \mathbf {x}_k)}{ 8 \pi \mu } + \cdots \end{aligned}$$
and the stresslet \(\mathbf {S}_{k,j}^{(1)} \) is
$$\begin{aligned} \mathbf {S}_{k,j}^{(1)} = \dfrac{20}{3} \pi \mu R_k^3 \big ( 1 + \dfrac{R_k^2}{10} \nabla ^2 \big ) \mathbf {E}^{(0)}_j \Big |_{\mathbf {x} = \mathbf {x}_k} \end{aligned}$$
where \(\mathbf {E}^{(0)}_j\) is the rate of deformation resulting from \(\mathbf {u}_j\).
To compute \(\mathbf {U}_i^{(2,f)}\), we follow the computation framework provided in (Kim and Karrila 1991), with the algebra reduced from the system geometry. First we have
$$\begin{aligned} \mathbf {S}_{k,j}^{(1)}= & {} \Big [ - \dfrac{5}{2} \dfrac{R_k^3}{l_{kj}^2} + \dfrac{3}{2} \dfrac{R_k^5}{l_{kj}^4} \Big ( 1 + \dfrac{5}{3} \dfrac{R_j^2}{R_k^2} \Big ) \Big ] \big ( \mathbf {d}_{jk} \mathbf {d}_{jk} - \dfrac{1}{3} \mathbf {I} \big ) \mathbf {d}_{jk} \cdot \mathbf {F}_j \\&- \,\dfrac{1}{2} \dfrac{R_k^5}{l_{kj}^4} \Big ( 1 + \dfrac{5}{3} \dfrac{R_j^2}{R_k^2} \Big ) \Big ( \mathbf {F}_j \mathbf {d}_{jk} + \mathbf {d}_{jk} \mathbf {F}_j - 2 \mathbf {d}_{jk} \mathbf {d}_{jk} \mathbf {d}_{jk} \cdot \mathbf {F}_j \Big ) \end{aligned}$$
where
$$\begin{aligned} \mathbf {d}_{jk} = \dfrac{\mathbf {x}_k - \mathbf {x}_j}{l_{kj}} = \text {sign} (k - j) \mathbf {e}_x, \quad \mathbf {F}_j = F_j \mathbf {e}_x \end{aligned}$$
thus
$$\begin{aligned} \mathbf {S}_{k,j}^{(1)} = F_j \text {sign} (k-j) \Big [ - \dfrac{5}{2} \dfrac{R_k^3}{l_{kj}^2} + \dfrac{3}{2} \dfrac{R_k^5}{l_{kj}^4} \Big ( 1 + \dfrac{5}{3} \dfrac{R_j^2}{R_k^2} \Big ) \Big ] \big ( \mathbf {e}_x \mathbf {e}_x - \dfrac{1}{3} \mathbf {I} \big ) \end{aligned}$$
Let
$$\begin{aligned} \varLambda _{k,j} = \text {sign} (k-j) \Big [ - \dfrac{5}{2} \dfrac{R_k^3}{l_{kj}^2} + \dfrac{3}{2} \dfrac{R_k^5}{l_{kj}^4} \Big ( 1 + \dfrac{5}{3} \dfrac{R_j^2}{R_k^2} \Big ) \Big ] \end{aligned}$$
after some direct calculation, we obtain
$$\begin{aligned} \mathbf {u}_{jk}^{(1)} =\big [ F_j \varLambda _{k,j} \big ( \mathbf {e}_x \mathbf {e}_x - \dfrac{1}{3} \mathbf {I} \big ) \cdot \nabla \big ] \cdot \dfrac{\mathbf {G} (\mathbf {x} - \mathbf {x}_k)}{ 8 \pi \mu } = \dfrac{F_j \varLambda _{k,j}}{ 8 \pi \mu } \Big ( \dfrac{\mathbf {r}}{r^3} - \dfrac{3 r_x^2}{r^5} \mathbf {r} \Big ) \end{aligned}$$
thus
$$\begin{aligned}&\Big ( 1 + \dfrac{R_i^2}{6} \Big ) \nabla ^2 \mathbf {u}_{jk}^{(1)} \Big |_{\mathbf {x} = \mathbf {x}_i} \\&\quad = \dfrac{F_j \varLambda _{k,j}}{ 8 \pi \mu } \Big [ \dfrac{\mathbf {x}_i {-} \mathbf {x}_k}{ |\mathbf {x}_i {-} \mathbf {x}_k |^3} {-} \dfrac{3 \big ( (\mathbf {x}_i - \mathbf {x}_k) \cdot \mathbf {e}_x \big )^2}{|\mathbf {x}_i - \mathbf {x}_k |^5} (\mathbf {x}_i - \mathbf {x}_k)+ \dfrac{R_i^2}{6} \nabla ^2 \Big ( \dfrac{\mathbf {r}}{r^3} - \dfrac{3 r_x^2}{r^5} \mathbf {r} \Big ) \Big |_{\mathbf {x} = \mathbf {x}_i} \Big ] \\&\quad \sim \dfrac{F_j }{ 8 \pi \mu } \text {sign} (k-j) \Big ( - \dfrac{5}{2} \dfrac{R_k^3}{l_{kj}^2} + O \big ( \dfrac{1}{l_{kj}^4} \big ) \Big )\Big ( - \dfrac{2 \text {sign} (i-k)}{l_{ik}^2} \mathbf {e}_x + O \big ( \dfrac{1}{l_{ik}^4} \big ) \Big ) \\&\quad = \dfrac{F_j }{ 8 \pi \mu } \text {sign} (k-j) \text {sign} (i-k) \dfrac{5 R_k^3}{l_{kj}^2 l_{ik}^2} \mathbf {e}_x + O \big ( \dfrac{1}{l^6} \big ) \end{aligned}$$
Finally we get
$$\begin{aligned} \mathbf {U}_i^{(2,f)}= & {} \Big ( 1 + \dfrac{R_i^2}{6} \Big ) \nabla ^2 \sum _{j,k}^{k \ne i,j} \mathbf {u}_{jk}^{(1)} \Big |_{\mathbf {x} = \mathbf {x}_i} \\= & {} \sum _j \dfrac{F_j }{ 8 \pi \mu } \sum _{k \ne i,j} \text {sign} (k-j) \text {sign} (i-k) \dfrac{5 R_k^3}{l_{kj}^2 l_{ik}^2} \mathbf {e}_x + O \big ( \dfrac{1}{l^6} \big ) \end{aligned}$$
after non-dimensionalization, it gives
$$\begin{aligned} \mathbf {U}_i^{(2,f)}= & {} \Big ( 1 + \dfrac{R_i^2}{6} \Big ) \nabla ^2 \sum _{j,k}^{k \ne i,j} \mathbf {u}_{jk}^{(1)} \Big |_{\mathbf {x} = \mathbf {x}_i} \\= & {} \sum _j \dfrac{15}{4} F_j \delta ^4 \sum _{k \ne i,j} \text {sign} (k-j) \text {sign} (i-k) \dfrac{ R_k^3}{l_{kj}^2 l_{ik}^2} \mathbf {e}_x + O \big ( \delta ^6 \big ) \end{aligned}$$
Our analysis in Appendix B shows that \(\mathbf {U}_i^{(2,e)} \sim O (\delta ^5)\), therefore
$$\begin{aligned} \mathbf {U}_i^{(2)} = \sum _j \dfrac{15}{4} F_j \delta ^4 \sum _{k \ne i,j} \text {sign} (k-j) \text {sign} (i-k) \dfrac{ R_k^3}{l_{kj}^2 l_{ik}^2} \mathbf {e}_x + O \big ( \delta ^5 \big ) \end{aligned}$$
With the leading terms from the second reflection added to the system, the algorithm given at the beginning of this part is modified as \(A_{12} = (a_{ij} + \widetilde{a}_{ij})\), where \(a_{ij}\) is given by Eq. (E.2) and
$$\begin{aligned} \widetilde{a}_{ij} = \dfrac{5}{8 \pi } \sum _{k \ne i,j} \text {sign} (k-j) \text {sign} (i-k) \dfrac{ R_k^3}{l_{kj}^2 l_{ik}^2} \end{aligned}$$
F Asymptotic analysis of the three systems consisting of two hobbled PMPYs
For simplicity, we denote the distance between any two spheres i and j by \(l_{ij}\). For example, \(l_{13} = l_{12} + l_{23}\).
1.1 F.1 System A (two dumb-bells) with controls in \((\dot{l}_I, \dot{l}_{II})\)
The asymptotic behavior of the velocity of the spheres is
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{6 \pi \mu R_1} + \dfrac{F_2}{4 \pi \mu l_{12}} + \dfrac{F_3}{4 \pi \mu l_{13}} + \dfrac{F_4}{4 \pi \mu l_{14}} \\ U_2\sim & {} \dfrac{F_1}{4 \pi \mu l_{12}} + \dfrac{F_2}{6 \pi \mu R_2} + \dfrac{F_3}{4 \pi \mu l_{23}} + \dfrac{F_4}{4 \pi \mu l_{24}}\\ U_3\sim & {} \dfrac{F_1}{4 \pi \mu l_{13}} + \dfrac{F_2}{4 \pi \mu l_{23}} + \dfrac{F_3}{6 \pi \mu R_3} + \dfrac{F_4}{4 \pi \mu l_{34}}\\ U_4\sim & {} \dfrac{F_1}{4 \pi \mu l_{14}} + \dfrac{F_2}{4 \pi \mu l_{24}} + \dfrac{F_3}{4 \pi \mu l_{34}} + \dfrac{F_4}{6 \pi \mu R_4} \end{aligned}$$
with relations and constraints
$$\begin{aligned} U_2 - U_1= & {} \dot{l}_{12} = \xi _{I}, \quad U_4 - U_3 = \dot{l}_{34} = \xi _{II} \\ F_1 + F_2= & {} 0, \quad F_3 + F_4 = 0. \end{aligned}$$
After scaling with hat notation omitted, the system becomes
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{R_1} + \dfrac{3}{2} \Big [ \dfrac{F_2}{l_{12}} + \dfrac{F_3}{l_{13}} + \dfrac{F_4}{l_{14}} \Big ] \delta \\ U_2\sim & {} \dfrac{F_2}{R_2} + \dfrac{3}{2} \Big [ \dfrac{F_1}{l_{12}} + \dfrac{F_3}{l_{23}} + \dfrac{F_4}{l_{24}} \Big ] \delta \\ U_3\sim & {} \dfrac{F_3}{R_3} + \dfrac{3}{2} \Big [ \dfrac{F_1}{l_{13}} + \dfrac{F_2}{l_{23}} + \dfrac{F_4}{l_{34}} \Big ] \delta \\ U_4\sim & {} \dfrac{F_4}{R_4} + \dfrac{3}{2} \Big [ \dfrac{F_1}{l_{14}} + \dfrac{F_2}{l_{24}} + \dfrac{F_3}{l_{34}} \Big ] \delta \\ U_2 - U_1 = \dot{l}_{12}= & {} \xi _{I}, \quad U_4 - U_3 = \dot{l}_{34} = \xi _{II} \\ F_1 + F_2= & {} 0, \quad F_3 + F_4 = 0. \end{aligned}$$
With \(F_2 = - F_1, \ F_4 = -F_3\), the system is simplified to
$$\begin{aligned} U_1\sim & {} F_1 \Big ( \dfrac{1}{R_1} - \dfrac{3 \delta }{2 l_{12}} \Big ) + \dfrac{3}{2} F_3 \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} \Big ) \\ U_2\sim & {} F_1 \Big ( \dfrac{3 \delta }{2 l_{12}} - \dfrac{1}{R_2} \Big ) + \dfrac{3}{2} F_3 \delta \Big ( \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big ) \\ U_3\sim & {} \dfrac{3}{2} F_1 \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} \Big ) + F_3 \Big ( \dfrac{1}{R_3} - \dfrac{3 \delta }{2 l_{34}} \Big ) \\ U_4\sim & {} \dfrac{3}{2} F_1 \delta \Big ( \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) + F_3 \Big ( \dfrac{3 \delta }{2 l_{34}} - \dfrac{1}{R_3} \Big ). \end{aligned}$$
When \(R_1 = R_2 = R_3 = R_4 = R\),
$$\begin{aligned} \xi _I= & {} U_2 - U_1 \sim - F_1 \Big ( \dfrac{1}{R_1} + \dfrac{1}{R_2} \Big ) \quad \Rightarrow \quad F_1 = -\dfrac{R}{2} \xi _I \\ \xi _{II}= & {} U_4 - U_3 \sim - F_3 \Big ( \dfrac{1}{R_3} + \dfrac{1}{R_4} \Big ) \quad \Rightarrow \quad F_3 = -\dfrac{R}{2} \xi _{II} . \end{aligned}$$
Velocities of the PMPYs:
$$\begin{aligned} \overline{U}_I= & {} \dfrac{1}{2} \Big ( U_1 + U_2 \Big ) = \dfrac{1}{2} F_1 \Big ( \dfrac{1}{R_1} - \dfrac{1}{R_2} \Big ) + \dfrac{3}{4} F_3 \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} + \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big )\\&\sim - \dfrac{3}{8} R \xi _{II} \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} + \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big ) \\ \overline{U}_{II}= & {} \dfrac{1}{2} \Big ( U_3 + U_4 \Big ) = \dfrac{3}{4} F_1 \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} + \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) + \dfrac{1}{2} F_1 \Big ( \dfrac{1}{R_3} - \dfrac{1}{R_4} \Big )\\&\sim - \dfrac{3}{8} R \xi _{I} \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} + \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) \end{aligned}$$
Power of the PMPYs:
$$\begin{aligned} P_I= & {} F_1 U_1 + F_2 U_2 = F_1 \big ( U_1 - U_2 \big ) = - F_1 \xi _I = \dfrac{R}{2} \xi _I^2 \\ P_{II}= & {} F_3 U_3 + F_4 U_4 = F_3 \big ( U_3 - U_4 \big ) = - F_3 \xi _{II} = \dfrac{R}{2} \xi _{II}^2 \end{aligned}$$
However, we observe that although \(\overline{U}_{I}, \overline{U}_{II} \) scale like \(O (\delta )\), the net translations \(X_{I}, X_{II}\) do not. Without loss of generality, we consider the first integral term in \(X_{I }\):
$$\begin{aligned} \int \overline{U}_{I} d t =- \dfrac{3}{8} R \delta \int _0^1 \dfrac{\xi _{II} (t)}{ l_{13} (t)} dt \end{aligned}$$
\(l_{13}\) can be written as \(l_{13} = l_{12} + l_{23} = 2 + \varDelta l_{12} + \varDelta l_{23}\), where \(\varDelta l_{12}, \varDelta l_{23} \sim O(\delta )\), thus
$$\begin{aligned} \dfrac{1}{l_{13}} = \dfrac{1}{2 + \varDelta l_{12} + \varDelta l_{23}} = \dfrac{1}{2} - \dfrac{\varDelta l_{12} + \varDelta l_{23}}{4} + O (\delta ^2) \end{aligned}$$
and
$$\begin{aligned} - \dfrac{3}{8} R \delta \int _0^1 \dfrac{\xi _{II} (t)}{ l_{13} (t)} dt= & {} - \dfrac{3}{8} R \delta \int _0^1 \xi _{II} \Big ( \dfrac{1}{2} - \dfrac{\varDelta l_{12} + \varDelta l_{23}}{4} \Big ) dt + O (\delta ^3) \\= & {} - \dfrac{3}{16} R \delta \int _0^1 \xi _{II} dt + \dfrac{3}{32} R \delta \int _0^1 \xi _{II} ( \varDelta l_{12} + \varDelta l_{23} ) dt + O (\delta ^3). \end{aligned}$$
The first integral vanishes since it is path-independent, the second one is an \(O (\delta ^2)\) term, hence
$$\begin{aligned} - \dfrac{3}{8} R \delta \int _0^1 \dfrac{\xi _{II} (t)}{ l_{13} (t)} dt \sim O (\delta ^2). \end{aligned}$$
A similar argument applies to all other integrals in \(X_{I}, X_{II}\), thus at most \(X_{I}, X_{II} \sim O (\delta ^2)\).
When the radii are not all equal, the leading order term of \(\overline{U}_{I}, \overline{U}_{II} \) scales as O(1), but this does not contribute to the net translations and we still have \(X_{I}, X_{II} \sim O (\delta ^2)\). This is because the leading order terms are of the form \(\varPhi \xi (t)\), where the coefficient \(\varPhi \) depends on the radii only, thus \(\int \varPhi \xi dt\) is again path-independent. Also in this case, the \(O(\delta )\) terms in \(\overline{U}_{I}, \overline{U}_{II} \) become more complicated, but they are still of the form \(\varPhi \xi / l_{ij}\), where \(\varPhi \) depends on the radii only, and the same argument above applies, thus in the end we have \(X_{I}, X_{II} \sim O (\delta ^2)\).
1.2 F.2 System B with controls in \((\dot{R}_1, \dot{R}_3)\)
The asymptotic behavior of the velocity of each sphere is
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{6 \pi \mu R_1} + \Big [ \dfrac{F_2}{4 \pi \mu l_{12}} - \Big ( \dfrac{R_2}{l_{12}} \Big )^2 \dot{R}_2 \Big ] + \Big [ \dfrac{F_3}{4 \pi \mu l_{13}} - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \dot{R}_3 \Big ] \\&+ \,\Big [ \dfrac{F_4}{4 \pi \mu l_{14}} - \Big ( \dfrac{R_4}{l_{14}} \Big )^2 \dot{R}_4 \Big ] \\ U_2\sim & {} \dfrac{F_2}{6 \pi \mu R_2} + \Big [ \dfrac{F_1}{4 \pi \mu l_{12}} + \Big ( \dfrac{R_1}{l_{12}} \Big )^2 \dot{R}_1 \Big ] + \Big [ \dfrac{F_3}{4 \pi \mu l_{23}} - \Big ( \dfrac{R_3}{l_{23}} \Big )^2 \dot{R}_3 \Big ] \\&+\, \Big [ \dfrac{F_4}{4 \pi \mu l_{24}} - \Big ( \dfrac{R_4}{l_{24}} \Big )^2 \dot{R}_4 \Big ] \\ U_3\sim & {} \dfrac{F_3}{6 \pi \mu R_3} + \Big [ \dfrac{F_1}{4 \pi \mu l_{13}} + \Big ( \dfrac{R_1}{l_{13}} \Big )^2 \dot{R}_1 \Big ] + \Big [ \dfrac{F_2}{4 \pi \mu l_{23}} + \Big ( \dfrac{R_2}{l_{23}} \Big )^2 \dot{R}_2 \Big ] \\&+ \,\Big [ \dfrac{F_4}{4 \pi \mu l_{34}} - \Big ( \dfrac{R_4}{l_{34}} \Big )^2 \dot{R}_4 \Big ] \\ U_4\sim & {} \dfrac{F_4}{6 \pi \mu R_4} + \Big [ \dfrac{F_1}{4 \pi \mu l_{14}} + \Big ( \dfrac{R_1}{l_{14}} \Big )^2 \dot{R}_1 \Big ] + \Big [ \dfrac{F_2}{4 \pi \mu l_{24}} + \Big ( \dfrac{R_2}{l_{24}} \Big )^2 \dot{R}_2 \Big ] \\&+ \,\Big [ \dfrac{F_3}{4 \pi \mu l_{34}} + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \dot{R}_3 \Big ] \end{aligned}$$
with relations
$$\begin{aligned} U_2 - U_1= & {} 0, \quad U_4 - U_3 = 0 \\ F_1 + F_2= & {} 0, \quad F_3 + F_4 = 0 \\ R_1^2 \dot{R}_1 + R_2^2 \dot{R}_2= & {} 0 \quad \Rightarrow \quad R_2^2 \zeta _2 = - R_1^2 \zeta _1 \\ R_3^2 \dot{R}_3 + R_4^2 \dot{R}_4= & {} 0 \quad \Rightarrow \quad R_4^2 \zeta _4 = - R_3^2 \zeta _3 . \end{aligned}$$
After scaling with hat notation omitted
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{R_1} + \Big [ \dfrac{3 F_2}{2 l_{12}} \delta - \Big (\dfrac{R_2}{l_{12}} \Big )^2 \zeta _2 \delta ^2 \Big ] + \Big [ \dfrac{3 F_3}{2 l_{13}} \delta - \Big (\dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 \delta ^2 \Big ] \\&+\, \Big [ \dfrac{3 F_4}{2 l_{14}} \delta - \Big (\dfrac{R_4}{l_{14}} \Big )^2 \zeta _4 \delta ^2 \Big ] \\ U_2\sim & {} \dfrac{F_2}{R_2} + \Big [ \dfrac{3 F_1}{2 l_{12}} \delta + \Big (\dfrac{R_1}{l_{12}} \Big )^2 \zeta _1 \delta ^2 \Big ] + \Big [ \dfrac{3 F_3}{2 l_{23}} \delta - \Big (\dfrac{R_3}{l_{23}} \Big )^2 \zeta _3 \delta ^2 \Big ] \\&+\, \Big [ \dfrac{3 F_4}{2 l_{24}} \delta - \Big (\dfrac{R_4}{l_{24}} \Big )^2 \zeta _4 \delta ^2 \Big ] \\ U_3\sim & {} \dfrac{F_3}{R_3} + \Big [ \dfrac{3 F_1}{2 l_{13}} \delta + \Big (\dfrac{R_1}{l_{13}} \Big )^2 \zeta _1 \delta ^2 \Big ] + \Big [ \dfrac{3 F_2}{2 l_{23}} \delta + \Big (\dfrac{R_3}{l_{23}} \Big )^2 \zeta _2 \delta ^2 \Big ] \\&+\, \Big [ \dfrac{3 F_4}{2 l_{34}} \delta - \Big (\dfrac{R_4}{l_{34}} \Big )^2 \zeta _4 \delta ^2 \Big ] \\ U_4\sim & {} \dfrac{F_4}{R_4} + \Big [ \dfrac{3 F_1}{2 l_{14}} \delta + \Big (\dfrac{R_1}{l_{14}} \Big )^2 \zeta _1 \delta ^2 \Big ] + \Big [ \dfrac{3 F_2}{2 l_{24}} \delta + \Big (\dfrac{R_3}{l_{24}} \Big )^2 \zeta _2 \delta ^2 \Big ] \\&+\, \Big [ \dfrac{3 F_3}{2 l_{34}} \delta + \Big (\dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \Big ]. \end{aligned}$$
With \(F_2 = - F_1, \ F_4 = - F_3\), the system becomes
$$\begin{aligned} U_1\sim & {} F_1 \Big ( \dfrac{1}{R_1} - \dfrac{3 \delta }{2 l_{12}} \Big ) + \dfrac{3 F_3}{2} \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} \Big )\\&+\, \delta ^2 \Big [ - \Big ( \dfrac{R_2}{l_{12}} \Big )^2 \zeta _2 - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 - \Big ( \dfrac{R_4}{l_{14}} \Big )^2 \zeta _4 \Big ] \\ U_2\sim & {} F_1 \Big ( - \dfrac{1}{R_2} + \dfrac{3 \delta }{2 l_{12}} \Big ) + \dfrac{3 F_3}{2} \delta \Big ( \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big )\\&+\, \delta ^2 \Big [ \Big ( \dfrac{R_1}{l_{12}} \Big )^2 \zeta _1 - \Big ( \dfrac{R_3}{l_{23}} \Big )^2 \zeta _3 - \Big ( \dfrac{R_4}{l_{24}} \Big )^2 \zeta _4 \Big ] \\ U_3\sim & {} \dfrac{3 F_1}{2} \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} \Big ) + F_3 \Big ( \dfrac{1}{R_3} - \dfrac{3 \delta }{2 l_{34}} \Big ) \\&+\, \delta ^2 \Big [ \Big ( \dfrac{R_1}{l_{13}} \Big )^2 \zeta _1 + \Big ( \dfrac{R_2}{l_{23}} \Big )^2 \zeta _2 - \Big ( \dfrac{R_4}{l_{34}} \Big )^2 \zeta _4 \Big ] \\ U_4\sim & {} \dfrac{3 F_1}{2} \delta \Big ( \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) + F_3 \Big ( - \dfrac{1}{R_4} + \dfrac{3 \delta }{2 l_{34}} \Big ) \\&+\, \delta ^2 \Big [ \Big ( \dfrac{R_1}{l_{14}} \Big )^2 \zeta _1 + \Big ( \dfrac{R_2}{l_{24}} \Big )^2 \zeta _2 + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \Big ]. \end{aligned}$$
Expand \(F_1, F_3\) as
$$\begin{aligned} F_1 = F_1^0 + \delta F_1^1 + \delta ^2 F_1^2 + O (\delta ^3), \quad F_3 = F_3^0 + \delta F_3^1 + \delta ^2 F_3^2 + O (\delta ^3); \end{aligned}$$
then
$$\begin{aligned} U_1\sim & {} \dfrac{F_1^0}{R_1} + \delta \dfrac{F_1^1}{R_1} - \delta \dfrac{3 F_1^0}{2 l_{12}} + \delta ^2 \dfrac{F_1^2}{R_1} - \delta ^2 \dfrac{3 F_1^1}{2 l_{12}} + \dfrac{3}{2} \delta F_3^0 \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} \Big ) \\&+\, \dfrac{3}{2} \delta ^2 F_3^1 \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} \Big ) \\&+ \,\delta ^2 \Big [ - \Big ( \dfrac{R_2}{l_{12}} \Big )^2 \zeta _2 - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 - \Big ( \dfrac{R_4}{l_{14}} \Big )^2 \zeta _4 \Big ] + O (\delta ^3) \\ U_2\sim & {} - \dfrac{F_1^0}{R_2} - \delta \dfrac{F_1^1}{R_2} + \delta \dfrac{3 F_1^0}{2 l_{12}} - \delta ^2 \dfrac{F_1^2}{R_2} + \delta ^2 \dfrac{3 F_1^1}{2 l_{12}}\\&+\, \dfrac{3}{2} \delta F_3^0 \Big ( \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big ) + \dfrac{3}{2} \delta ^2 F_3^1 \Big ( \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big ) \\&+\, \delta ^2 \Big [ \Big ( \dfrac{R_1}{l_{12}} \Big )^2 \zeta _1 - \Big ( \dfrac{R_3}{l_{23}} \Big )^2 \zeta _3 - \Big ( \dfrac{R_4}{l_{24}} \Big )^2 \zeta _4 \Big ] + O (\delta ^3) \\ U_3\sim & {} \dfrac{F_3^0}{R_3} + \delta \dfrac{F_3^1}{R_3} - \delta \dfrac{3 F_3^0}{2 l_{34}} + \delta ^2 \dfrac{F_3^2}{R_3} - \delta ^2 \dfrac{3 F_3^1}{2 l_{34}}\\&+\, \dfrac{3}{2} \delta F_1^0 \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} \Big ) + \dfrac{3}{2} \delta ^2 F_1^1 \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} \Big ) \\&+\, \delta ^2 \Big [ \Big ( \dfrac{R_1}{l_{13}} \Big )^2 \zeta _1 + \Big ( \dfrac{R_2}{l_{23}} \Big )^2 \zeta _2 - \Big ( \dfrac{R_4}{l_{34}} \Big )^2 \zeta _4 \Big ] + O (\delta ^3) \\ U_4\sim & {} - \dfrac{F_3^0}{R_4} - \delta \dfrac{F_3^1}{R_4} + \delta \dfrac{3 F_3^0}{2 l_{34}} - \delta ^2 \dfrac{F_3^2}{R_4} + \delta ^2 \dfrac{3 F_3^2}{2 l_{34}}\\&+\, \dfrac{3}{2} \delta F_1^0 \Big ( \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) + \dfrac{3}{2} \delta ^2 F_1^1 \Big ( \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) \\&+\, \delta ^2 \Big [ \Big ( \dfrac{R_1}{l_{14}} \Big )^2 \zeta _1 + \Big ( \dfrac{R_2}{l_{24}} \Big )^2 \zeta _2 + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \Big ] + O (\delta ^3). \end{aligned}$$
Compare the O(1) terms:
$$\begin{aligned} U_1^0 = U_2^0 \ \Rightarrow \ \dfrac{F_1^0}{R_1} = - \dfrac{F_1^0}{R_2} \ \Rightarrow \ F_1^0 = 0, \quad \text {similarly, } \quad F_3^0 = 0. \end{aligned}$$
Compare the \(O (\delta )\) terms:
$$\begin{aligned} U_1^1 = U_2^1 \ \Rightarrow \ \dfrac{F_1^1}{R_1} = - \dfrac{F_1^1}{R_2} \ \Rightarrow \ F_1^1 = 0, \quad \text {similarly, } \quad F_3^1 = 0. \end{aligned}$$
Compare the \(O (\delta ^2)\) terms:
$$\begin{aligned} U_1^2= & {} \dfrac{F_1^2}{R_1} + \Big [ - \Big ( \dfrac{R_2}{l_{12}} \Big )^2 \zeta _2 - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 - \Big ( \dfrac{R_4}{l_{14}} \Big )^2 \zeta _4 \Big ] \\ U_2^2= & {} - \dfrac{F_1^2}{R_2} + \Big [ \Big ( \dfrac{R_1}{l_{12}} \Big )^2 \zeta _1 - \Big ( \dfrac{R_3}{l_{23}} \Big )^2 \zeta _3 - \Big ( \dfrac{R_4}{l_{24}} \Big )^2 \zeta _4 \Big ] \\ U_1^2 = U_2^2\Rightarrow & {} F_1^2 = \dfrac{R_1 R_2}{R_1 + R_2} \Big ( \dfrac{1}{l_{13}^2} - \dfrac{1}{l_{23}^2} - \dfrac{1}{l_{14}^2} + \dfrac{1}{l_{24}^2} \Big ) R_3^2 \zeta _3 \end{aligned}$$
and similarly,
$$\begin{aligned} U_3^2= & {} \dfrac{F_3^2}{R_3} + \Big [ \Big ( \dfrac{R_1}{l_{13}} \Big )^2 \zeta _1 + \Big ( \dfrac{R_2}{l_{23}} \Big )^2 \zeta _2 - \Big ( \dfrac{R_4}{l_{34}} \Big )^2 \zeta _4 \Big ] \\ U_4^2= & {} - \dfrac{F_3^2}{R_4} + \Big [ \Big ( \dfrac{R_1}{l_{14}} \Big )^2 \zeta _1 + \Big ( \dfrac{R_2}{l_{24}} \Big )^2 \zeta _2 + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \Big ] \\ U_3^2 = U_4^2\Rightarrow & {} F_3^2 = \dfrac{R_3 R_4}{R_3 + R_4} \Big ( \dfrac{1}{l_{14}^2} - \dfrac{1}{l_{13}^2} - \dfrac{1}{l_{24}^2} + \dfrac{1}{l_{23}^2} \Big ) R_1^2 \zeta _1. \end{aligned}$$
Velocities of the PMPYs:
$$\begin{aligned} U_I= & {} U_1 = U_2 = \dfrac{R_1^2}{l_{12}^2} \zeta _1 \delta ^2 + R_3^2 \zeta _3 \delta ^2 \Big [ \dfrac{R_1}{R_1 + R_2} \Big ( \dfrac{1}{l_{14}^2} - \dfrac{1}{l_{13}^2} \Big )\\&+\, \dfrac{R_2}{R_1 + R_2} \Big ( \dfrac{1}{l_{24}^2} - \dfrac{1}{l_{23}^2} \Big ) \Big ] \\ U_{II}= & {} U_3 = U_4 = \dfrac{R_3^2}{l_{34}^2} \zeta _3 \delta ^2 + R_1^2 \zeta _1 \delta ^2 \Big [ \dfrac{R_3}{R_3 + R_4} \Big ( \dfrac{1}{l_{13}^2} - \dfrac{1}{l_{23}^2} \Big )\\&+\, \dfrac{R_4}{R_3 + R_4} \Big ( \dfrac{1}{l_{14}^2} - \dfrac{1}{l_{24}^2} \Big ) \Big ] \end{aligned}$$
Power of the PMPYs:
$$\begin{aligned} P_I= & {} \dfrac{8}{3} \big ( R_1 \zeta _1^2 + R_2 \zeta _2^2 \big ) = \dfrac{8}{3} R_1 \dfrac{R_1^3 + R_2^3}{R_2^3} \zeta _1^2 \\ P_{II}= & {} \dfrac{8}{3} \big ( R_3 \zeta _3^2 + R_4 \zeta _4^2 \big ) = \dfrac{8}{3} R_3 \dfrac{R_3^3 + R_4^3}{R_4^3} \zeta _3^2 \end{aligned}$$
1.3 F.3 System C with controls in \((\dot{l}_{I}, \dot{R}_3)\)
The asymptotic behavior of the velocity of each sphere is
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{6 \pi \mu R_1} + \dfrac{F_2}{4 \pi \mu l_{12}} + \Big [ \dfrac{F_3}{4 \pi \mu l_{13}} - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \dot{R}_3 \Big ] + \Big [ \dfrac{F_4}{4 \pi \mu l_{14}} - \Big ( \dfrac{R_4}{l_{14}} \Big )^2 \dot{R}_4 \Big ] \\ U_2\sim & {} \dfrac{F_2}{6 \pi \mu R_2} + \dfrac{F_1}{4 \pi \mu l_{12}} + \Big [ \dfrac{F_3}{4 \pi \mu l_{23}} - \Big ( \dfrac{R_3}{l_{23}} \Big )^2 \dot{R}_3 \Big ] + \Big [ \dfrac{F_4}{4 \pi \mu l_{24}} - \Big ( \dfrac{R_4}{l_{24}} \Big )^2 \dot{R}_4 \Big ] \\ U_3\sim & {} \dfrac{F_3}{6 \pi \mu R_3} + \dfrac{F_1}{4 \pi \mu l_{13}} + \dfrac{F_2}{4 \pi \mu l_{23}} + \Big [ \dfrac{F_4}{4 \pi \mu l_{34}} - \Big ( \dfrac{R_4}{l_{34}} \Big )^2 \dot{R}_4 \Big ] \\ U_4\sim & {} \dfrac{F_4}{6 \pi \mu R_4} + \dfrac{F_1}{4 \pi \mu l_{14}} + \dfrac{F_2}{4 \pi \mu l_{24}} + \Big [ \dfrac{F_3}{4 \pi \mu l_{34}} + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \dot{R}_3 \Big ] \end{aligned}$$
with relations
$$\begin{aligned} U_2 - U_1= & {} \dot{l}_{12} = \xi _I, \quad U_4 - U_3 = 0 \\ F_1 + F_2= & {} 0 , \quad F_3 + F_4 = 0 \\ R_3^2 \zeta _3 + R_4^2 \zeta _4= & {} 0 \ \Rightarrow \ R_4^2 \zeta _4 = - R_3^2 \zeta _3. \end{aligned}$$
After scaling
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{R_1} + \dfrac{3 F_2}{2 l_{12}} \delta + \Big [ \dfrac{2 F_3}{2 l _{13}} \delta - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 \delta ^2 \Big ] + \Big [ \dfrac{3 F_4}{2 l_{14}} \delta - \Big ( \dfrac{R_4}{l_{14}} \Big )^2 \zeta _4 \delta ^2 \Big ] \\ U_2\sim & {} \dfrac{F_2}{R_2} + \dfrac{3 F_1}{2 l_{12}} \delta + \Big [ \dfrac{2 F_3}{2 l _{23}} \delta - \Big ( \dfrac{R_3}{l_{23}} \Big )^2 \zeta _3 \delta ^2 \Big ] + \Big [ \dfrac{3 F_4}{2 l_{24}} \delta - \Big ( \dfrac{R_4}{l_{24}} \Big )^2 \zeta _4 \delta ^2 \Big ] \\ U_3\sim & {} \dfrac{F_3}{R_3} + \dfrac{3 F_1}{2 l_{13}} \delta + \dfrac{3 F_2}{2 l_{23}} \delta + \Big [ \dfrac{3 F_4}{2 l_{34}} \delta - \Big ( \dfrac{R_4}{l_{34}} \Big )^2 \zeta _4 \delta ^2 \Big ] \\ U_4\sim & {} \dfrac{F_4}{R_4} + \dfrac{3 F_1}{2 l_{14}} \delta + \dfrac{3 F_2}{2 l_{24}} \delta + \Big [ \dfrac{3 F_3}{2 l_{34}} \delta + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \Big ]. \end{aligned}$$
With \(F_2 = - F_1, \ F_4 = - F_3\), the system is simplified to
$$\begin{aligned} U_1\sim & {} \dfrac{F_1}{R_1} - \dfrac{3 F_1}{2 l_{12}} \delta + \Big [ \dfrac{3 F_3}{2 l_{13}} \delta - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 \delta ^2 \Big ] + \Big [ - \dfrac{3 F_3}{2 l_{14}} \delta + \Big ( \dfrac{R_3}{l_{14}} \Big )^2 \zeta _3 \delta ^2 \Big ] \\ U_2\sim & {} - \dfrac{F_1}{R_2} + \dfrac{3 F_1}{2 l_{12}} \delta + \Big [ \dfrac{3 F_3}{2 l_{23}} \delta - \Big ( \dfrac{R_3}{l_{13}} \Big )^2 \zeta _3 \delta ^2 \Big ] + \Big [ - \dfrac{3 F_3}{2 l_{24}} \delta + \Big ( \dfrac{R_3}{l_{24}} \Big )^2 \zeta _3 \delta ^2 \Big ] \\ U_3\sim & {} \dfrac{F_3}{R_3} + \dfrac{3 F_1}{2 l_{13}} \delta - \dfrac{3 F_1}{2 l_{23}} \delta + + \Big [ - \dfrac{3 F_3}{2 l_{34}} \delta + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \Big ] \\ U_4\sim & {} - \dfrac{F_3}{R_4} + \dfrac{3 F_1}{2 l_{14}} \delta - \dfrac{3 F_1}{2 l_{24}} \delta + + \Big [ \dfrac{3 F_3}{2 l_{34}} \delta + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \Big ]. \end{aligned}$$
For PMPY I,
$$\begin{aligned} \xi _I = U_2 - U_1 \sim - F_1 \big ( \dfrac{1}{R_1} + \dfrac{1}{R_2} \big ) \ \Rightarrow \ F_1 = - \dfrac{R_1 R_2}{R_1 + R_2} \xi _I, \end{aligned}$$
thus for PMPY II,
$$\begin{aligned} U_3\sim & {} \dfrac{F_3}{R_3} - \dfrac{3}{2} \dfrac{R_1 R_2}{R_1 + R_2} \xi _I \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} \Big ) - \dfrac{3 F_3}{2 l_{34}} \delta + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \\ U_4\sim & {} - \dfrac{F_3}{R_4} - \dfrac{3}{2} \dfrac{R_1 R_2}{R_1 + R_2} \xi _I \delta \Big ( \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) + \dfrac{3 F_3}{2 l_{34}} \delta + \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 . \end{aligned}$$
Expand \(F_3\) as \(F_3 = F_3^0 + \delta F_3^1 + \delta ^2 F_3^2 + O (\delta ^3)\),
$$\begin{aligned} U_3\sim & {} \dfrac{F_3^0}{R_3} + \delta \dfrac{F_3^1}{R_3} + \delta ^2 \dfrac{F_3^2}{R_3} - \dfrac{3}{2} \dfrac{R_1 R_2}{R_1 + R_2} \xi _I \delta \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} \Big ) - \dfrac{3 F_3^0}{2 l _{34}} \delta - \dfrac{3 F_3^1}{2 l_{34}} \delta ^2 \\&+\, \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \\ U_4\sim & {} - \dfrac{F_3^0}{R_4} - \delta \dfrac{F_3^1}{R_4} - \delta ^2 \dfrac{F_3^2}{R_4} - \dfrac{3}{2} \dfrac{R_1 R_2}{R_1 + R_2} \xi _I \delta \Big ( \dfrac{1}{l_{14}} - \dfrac{1}{l_{24}} \Big ) + \dfrac{3 F_3^0}{2 l _{34}} \delta + \dfrac{3 F_3^1}{2 l_{34}} \delta ^2 \\&+\, \Big ( \dfrac{R_3}{l_{34}} \Big )^2 \zeta _3 \delta ^2 \end{aligned}$$
Compare the O(1) terms
$$\begin{aligned} U_3^0 = U_4^0 \ \Rightarrow \ \dfrac{F_3^0}{R_3} = - \dfrac{F_3^0}{R_4} \ \Rightarrow \ F_3^0 = 0. \end{aligned}$$
Compare the \(O ( \delta )\) terms
$$\begin{aligned} U_3^1 = U_4^1 \ \Rightarrow \ F_3^1 = \dfrac{3}{2} \dfrac{R_1 R_2}{R_1 + R_2} \dfrac{R_3 R_4}{R_3 + R_4} \xi _I \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{23}} - \dfrac{1}{l_{14}} + \dfrac{1}{l_{24}} \Big ) \end{aligned}$$
Velocities of the PMPYs:
$$\begin{aligned} \overline{U}_I= & {} \dfrac{1}{2} (U_1 + U_2) \\= & {} \dfrac{9}{8} \dfrac{R_1 R_2 R_3 R_4}{(R_1 + R_2) (R_3 + R_4)} \xi _I \delta ^2 \Big ( \dfrac{1}{l_{13}} - \dfrac{1}{l_{14}} + \dfrac{1}{l_{23}} - \dfrac{1}{l_{24}} \Big )^2\\&+ \,\dfrac{1}{2} R_3^2 \zeta _3 \delta ^2\Big ( \dfrac{1}{l_{14}^2} - \dfrac{1}{l_{13}^2} + \dfrac{1}{l_{24}^2} - \dfrac{1}{l_{23}^2} \Big ) \\ \overline{U}_{II}= & {} U_3 = U_4 \\&\sim \dfrac{3}{2} \dfrac{R_1 R_2}{R_1 + R_2} \xi _I \delta \Big [ \dfrac{R_3}{R_3 + R_4} \Big ( \dfrac{1}{l_{23}} - \dfrac{1}{l_{13}} \Big ) + \dfrac{R_4}{R_3 + R_4} \Big ( \dfrac{1}{l_{24}} - \dfrac{1}{l_{14}} \Big ) \Big ] \end{aligned}$$
Power of the PMPYs:
$$\begin{aligned} P_I= & {} F_1 U_1 + F_2 U_2 = F_1 (U_1 - U_2) = - F_1 \xi _I = \dfrac{R_1 R_2}{R_1 + R_2} \xi _I^2 \\ P_{II}= & {} \dfrac{8}{3} (R_3 \zeta _3^2 + R_4 \zeta _4^2) = \dfrac{8}{3} R_3 \dfrac{R_3^3 + R_4^3}{R_4^3} \zeta _3^2 \end{aligned}$$