Abstract
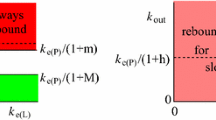
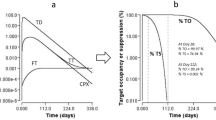
We consider the possibility of free receptor (antigen/cytokine) levels rebounding to higher than the baseline level after one or more applications of an antibody drug using a target-mediated drug disposition model. Using geometry and dynamical systems analysis, we show that rebound will occur if and only if the elimination rate of the drug–receptor product is slower than the elimination rates of the drug and of the receptor. We also analyse the magnitude of rebound through approximations and simulations and demonstrate that it increases if the drug dose increases or if the difference between the elimination rate of the drug–receptor product and the minimum of the elimination rates of the drug and of the receptor increases.
Access this article
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.










Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Agoram B, Martin S, van der Graaf P (2007) The role of mechanism-based pharmacokinetic-pharmacodynamic (pk-pd) modelling in translational research of biologics. Drug Discov Today 12:1018–1024
Ait-Oudhia S, Lowe P, Mager D (2012) Bridging clinical outcomes of canakinumab treatment in rheumatoid arthritis patients with a population model of il-1\(\beta \) kinetics. Pharmacomet Syst Pharmacol CPT. doi:10.1038/psp.2012.6
Aston P, Derks G, Raji A, Agoram B, van der Graaf P (2011) Mathematical analysis of the pharmacokinetic-pharmacodynamic (pkpd) behaviour of monoclonal antibodies: predicting in vivo potency. J Theor Biol 281:113–121
Aston P, Derks G, Agoram B, van der Graaf P (2012) A mathematical analysis of rebound in a target-mediated drug disposition model. II. With feedback. Abstract at VPH2012. http://www.vph-noe.eu/vph2012
Bhatia A, Kast R (2007) Tnf can paradoxically increase on etanercept treatment, occasionally contributing to TNF-mediated disease. J Rheum 34:447
Bravo Vergal Y, Hawkins N, Claxton K, Asseburg C, Palmer S, Woolacoot N, Bruce I, Sculpher M (2007) The cost-effectiveness of etanercept and infliximab for the treatment of patients with psoriatic arthritis. Rheumatology 46:1729–1735
Cacheux W, Boisserie T, Staudacher L, Vignaux O, Dousset B, Soubrane O, Terris B, Mateus C, Chaussade S, Goldwasser F (2008) Reversible tumor growth acceleration following bevacizumab interruption in metastatic colorectal cancer patients scheduled for surgery. Ann Onc 19:1659–1661
Chan J, Piper D, Cao Q, Liu D, King C, Wang W, Tang J, Liu Q, Higbee J, Xia A, Di Y, Shetterly S, Arimura Z, Salomonis H, Romanow W, Thibault S, Zhang R, Cao P, Yang X, Yu T, Lu M, Retter M, Kwon G, Henne K, Pan O, Tsai M, Fuchslocher B, Yang E, Zhou L, Lee K, Daris M, Sheng J, Wang Y, Shen W, Yeh W, Emery M, Walker N, Shan B, Schwarz M, Jackson S (2009) A proprotein convertase subtilisin/kexin type 9 neutralizing antibody reduces serum cholesterol in mice and nonhuman primates. Proc Natl Acad Sci USA 106:9820–9825
Fenichel N (1979) Geometric singular perturbation theory for ordinary differential equations. J Differ Equ 31:53–98
Haringman J, Gerlag D, Smeets T, Baeten D, van den Bosch F, Bresnihan B, Breedveld F, Dinant H, Legay F, Gram H, Loetscher P, Schmouder R, Woodworth T, Tak P (2006) A randomized controlled trial with an anti-ccl2 (anti-monocyte chemotactic protein 1) monoclonal antibody in patients with rheumatoid arthritis. Arthritis Rheum 54:2387–2392
Jordan D, Smith P (2007) Nonlinear ordinary differential equations, 4th edn. OUP, New York
Klein B, Zhang X, Lu Z, Bataille R (1995) Interleukin-6 in human multiple myeloma. Blood 85:863–872
Krippendorff D, Oyarzun B-F, Huisinga W (2009) Ligand accumulation counteracts therapeutic inhibition of receptor systems. In: Proceedings of foundations of systems biology in engeneering, FOSBE, pp 173–176
Levy G (1994) Pharmacologic target mediated drug disposition. Clin Pharmacol Therap 56:248–252
Lowe P, Tannenbaum S, Gautier A, Jimenez P (2009) Relationship between omalizumab pharmacokinetics, IgE pharmacodynamics and symptoms in patients with severe persistent allergic (IgE-mediated) asthma. Br J Clin Pharmacol 68:61–76
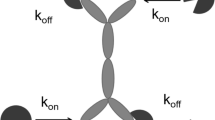
Mager D, Jusko W (2001) General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinet Pharmacodyn 28:507–532
Meno-Tetang G, Lowe P (2005) On the prediction of the human response: a recycled mechanistic pharmacokinetic/pharmacodynamic approach. Bas Clin Pharm Tox 96:182–192
Munafo A, Priestley A, Nestorov I, Visich J, Rogge M (2007) Safety, pharmacokinetics and pharmacodynamics of atacicept in healthy volunteers. Eur J Clin Pharmacol 63:647–656
Ng C, Stefanich E, Anand B, Fielder P, Vaickus L (2006) Pharmacokinetics/pharmacodynamics of nondepleting anti-CD4 monoclonal antibody (TRX1) in healthy human volunteers. Pharm Res 23:95–103
Peletier L, Gabrielsson J (2009) Dynamics of target-mediated drug disposition. Eur J Pharm Sci 38:445–464
Peletier L, Gabrielsson J (2012a) Dynamics of target-mediated drug disposition: characteristic profiles and parameter identification. J Pharmacokinet Pharmacodyn 39:429–451
Peletier L, Gabrielsson J (2012b) Dynamics of target-mediated drug disposition: how a drug reaches its target. Comput Geosc. doi:10.1007/s10596-012-9312-4
Smith H (1995) Monotone dynamical systems. In: An introduction to the theory of competitive and cooperative systems, Mathematical surveys and monographs, vol 41. AMS, Providence
Stefanini M, Wu F, Gabhann F, Popel A (2010) Increase of plasma vegf after intravenous administration of bevacizumab is predicted by a pharmacokinetic model. Cancer Res 70:9886–9894
Vugmeister Y, Tian X, Szlut P, Kasaian M, Xu X (2009) Pharmacokinetic and pharmacodynamics modeling of a humanized anti-IL-13 antibody in naive and ascaris-challenged cynomolgus monkeys. Pharmaceut Res 26:306–315
Wang B, Lau YY, Liang M, Vainshtein I, Zusmanovich M, Lu H, Magrini F, Sleeman M, Roskos L (2012) Mechanistic modeling of antigen sink effect for mavrilimumab following intravenous administration in patients with rheumatoid arthritis. J Clin Pharmacol 52:1150–1161
Acknowledgments
We are grateful for the input of Adewale Raji in the preliminary work for this paper. This preliminary stage was in part financially supported through the Biopharma Skills Project of the Universities of Surrey and Reading, jointly funded by the Higher Education Funding Council for England’s Economic Challenge Investment Fund (ECIF) and the South East England Development Agency (SEEDA).
Author information
Authors and Affiliations
Corresponding author
Appendix: Proofs of invariance and stability results
Appendix: Proofs of invariance and stability results
Proof of Lemma 2.1
The phase space is bounded by the three planes \(x=0, y=0\) and \(z=0\). If the vector field given by the Eqs. (4)–(6) at these planes is directed inside or is tangent to the octant, then the given region is invariant (Smith 1995).
Taking the inner product of the vector field with the inward pointing normal at the plane \(x=0\), we see from (4) that
and so \({\dot{x}}|_{x=0}\ge 0\) when \(z\ge 0\). Hence the vector field is directed inside the octant at the plane \(x=0\).
Similarly, from (5), we obtain
and so \({\dot{y}}|_{y=0}>0\) when \(z\ge 0\). In the same vein, from (6), we obtain
and so \({\dot{z}}|_{z=0}\ge 0\) when \(x,y\ge 0\).
Note that at the \(x\)-axis (\(y=z=0\)), the vector field is tangent to the plane \(z=0\), and is pointing inwards as \({\dot{y}}|_{y=z=0}=k_3\). At the \(y\)-axis (\(x=z=0\)), we have \({\dot{x}}=0\) and \({\dot{z}}=0\), hence \(x\) and \(z\) will stay zero for all time and the \(y\)-axis is invariant. On the \(y\)-axis, \({\dot{y}}>0\) if \(y<1\) and \({\dot{y}}<0\) is \(y>1\). Hence all orbits on the \(y\)-axis tend to the stable steady state at \(y=1\).
Thus, we can conclude that any trajectory with \(x(0), y(0), z(0)\ge 0\) must satisfy \(x(t), y(t), z(t)\ge 0\) for all \(t>0\). \(\square \)
Proof of Lemma 2.2
There are two steady state solutions of Eqs. (4)–(6), one of which is given by (7). The other solution is not in our phase space, and hence is not physically relevant, as the values of \(x\) and \(y\) are negative. \(\square \)
Proof of Corollary 2.4
By negating Lemma 2.3, it follows immediately that if the maximal \(v(\tau )\) value is above 1, then \(k_3>k_4\). And Lemma 2.3 implies that if \(k_3>k_4\), then \(v(\tau )\ge 1\) for all \(\tau \). We only have to show that \(v(\tau )\) cannot be equal to 1 for all time. This follows immediately with a contradiction argument. Assume that \(k_3>k_4\) and \(v(\tau )=1\) for all \(\tau \ge 1\). Then the \(v\)-dynamics (22) gives for all \(\tau \ge 0\) that \(0=(k_3-k_4)z\), hence \(z(\tau )=0\). Then (6) implies that \(0=\frac{xy}{\mu }\) for all \(\tau \ge 0\). However at \(\tau =0\), we have \(\frac{xy}{\mu }=\frac{1}{\mu }\). This is a contradiction, thus the assumption that \(v\equiv 1\) is false. \(\square \)
Proof of Theorem 2.5
In Lemma 2.3 we have shown that \(\lim _{\tau \rightarrow \infty }u(\tau )=0\). Since \(u=x+\mu z\) and \(x\) and \(z\) are non-negative functions, we conclude that \(\lim _{\tau \rightarrow \infty }x(\tau )= \lim _{t\rightarrow \infty }z(t)=0\) also. Hence, every trajectory will converge to a neighbourhood of the \(y\)-axis. We have also seen in Lemma 2.1 that the \(y\)-axis is invariant and that on this axis, all orbits tend to the stable steady state at \(y=1\). So intuitively it is clear that all trajectories will converge to the steady state (7) as \(\tau \rightarrow \infty \). To make this formal, we consider the \(y\)-dynamics in a neighbourhood of the \(y\)-axis.
Let \(\varepsilon >0\). Since \(\lim _{\tau \rightarrow \infty }x(\tau )= \lim _{\tau \rightarrow \infty }z(\tau )=0\), then there is some \(T>0\) such that for \(\tau >T\), we have
Thus with (5), we get for \(\tau >T\),
In other words, \(\frac{d}{d\tau }[e^{k_3(1+\varepsilon )\tau } (y-\frac{1}{1+\varepsilon })] \ge 0\) and \(\frac{d}{d\tau }[e^{k_3\tau }(y-(1+\varepsilon ))] \le 0\) and we can conclude that for \(\tau \ge T\)
Hence by choosing \(\varepsilon \) sufficiently small and for all \(\tau >T\) sufficiently large, we can make \(|y(\tau )-1|\) arbitrarily small. So we conclude that \(y(\tau )\rightarrow 1\) for \(\tau \rightarrow \infty \). \(\square \)
Proof of Lemma 2.7
This observation follows quickly from the expressions for the eigenvalues \(\lambda _1\) and \(\lambda _2\). Indeed, from (10) we find that
since \(k_2>0\) and hence the square root term is larger than the magnitude of the first term. Similarly, using (12) we get
\(\square \)
Proof of Lemma 2.8
Let \(k_2,k_4>0\) be fixed. Differentiating the expression for \(\lambda _1\), (10), with respect to \(k_1\) gives
The second term in the brackets is less than one in modulus (since \(k_2>0\)), and so this derivative is always negative. Thus, \(\lambda _1\) is a monotonically decreasing function of \(k_1\).
To derive the stated bounds on \(-\lambda _1\) that involve \(k_4\), we note that from (9) we have
When \(k_1<k_4\), the square root term in (29) always dominates the first term, and so \(\lambda _1+k_4>0\). When \(k_1=k_4\), we have
Finally, when \(k_1>k_4\), we note that \(1+k_1+k_2-k_4>0\) and in this case, the first term in (29) dominates the square root term and so we find that \(\lambda _1+k_4<0\).
Similarly, for the bounds on \(-\lambda _1\) involving \(k_1\), from (9) we obtain
The sign of \(\lambda +k_1\) is then obtained in the same way as for the sign of \(\lambda +k_4\) above. \(\square \)
Rights and permissions
About this article
Cite this article
Aston, P.J., Derks, G., Agoram, B.M. et al. A mathematical analysis of rebound in a target-mediated drug disposition model: I.Without feedback. J. Math. Biol. 68, 1453–1478 (2014). https://doi.org/10.1007/s00285-013-0675-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-013-0675-5
Mathematics Subject Classification
Profiles
- Gianne Derks View author profile