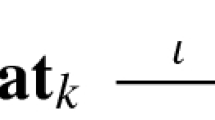Abstract
For a (co)monad T l on a category \({\mathcal{M}}\), an object X in \({\mathcal{M}}\) , and a functor \({{\varvec {\Pi}}:\mathcal{M} \to \mathcal{C}}\) , there is a (co)simplex \({Z^\ast:={\varvec {\Pi} {T_l}}^{\ast +1} X}\) in \({\mathcal{C}}\) . The aim of this paper is to find criteria for para-(co)cyclicity of Z *. Our construction is built on a distributive law of T l with a second (co)monad T r on \({\mathcal{M}}\) , a natural transformation \({i:{\varvec {\Pi} {T_l} \to {\bf \Pi} {T_r}}}\) , and a morphism \({w:{\varvec {T_r}}X \to {\varvec {T_l}}X}\) in \({\mathcal{M}}\) . The (symmetrical) relations i and w need to satisfy are categorical versions of Kaygun’s axioms of a transposition map. Motivation comes from the observation that a (co)ring T over an algebra R determines a distributive law of two (co)monads \({{\varvec {T_l}}=T \otimes_R (-)}\) and \({{\varvec {T_r}}=(-)\otimes_R T}\) on the category of R-bimodules. The functor Π can be chosen such that \({Z^n=T\widehat{\otimes}_R\cdots \widehat{\otimes}_R T \widehat{\otimes}_RX}\) is the cyclic R-module tensor product. A natural transformation \({{i}:T \widehat{\otimes}_R (-) \to (-) \widehat{\otimes}_R T}\) is given by the flip map and a morphism \({w: X \otimes_R T \to T\otimes_R X}\) is constructed whenever T is a (co)module algebra or coring of an R-bialgebroid. The notion of a stable anti-Yetter-Drinfel’d module over certain bialgebroids, the so-called × R -Hopf algebras, is introduced. In the particular example when T is a module coring of a × R -Hopf algebra \({\mathcal{B}}\) and X is a stable anti-Yetter-Drinfel’d \({\mathcal{B}}\) -module, the para-cyclic object Z * is shown to project to a cyclic structure on \({T^{\otimes_R\, \ast+1} \otimes_{\mathcal{B}} X}\) . For a \({\mathcal{B}}\) -Galois extension \({S \subseteq T}\) , a stable anti-Yetter-Drinfel’d \({\mathcal{B}}\) -module T S is constructed, such that the cyclic objects \({\mathcal{B}^{\otimes_R\, \ast+1} \otimes_{\mathcal{B}} T_S}\) and \({T^{\widehat{\otimes}_S\, \ast+1}}\) are isomorphic. This extends a theorem by Jara and Ştefan for Hopf Galois extensions. As an application, we compute Hochschild and cyclic homologies of a groupoid with coefficients in a stable anti-Yetter-Drinfel’d module, by tracing it back to the group case. In particular, we obtain explicit expressions for (coinciding relative and ordinary) Hochschild and cyclic homologies of a groupoid. The latter extends results of Burghelea on cyclic homology of groups.
Similar content being viewed by others
References
Akrami S.E., Majid S.: Braided cyclic cocycles and non-associative geometry. J. Math. Phys. 45, 3883–3911 (2004)
Beck J.: Distributive laws, Lecture Notes in Mathematics 80. Berlin-Heidelberg-New York: Springer Verlag (1969), pp. 119–140
Böhm G., Brzeziński T.: Strong connections and the relative Chern-Galois character for corings. Int. Math. Res. Not. 42, 2579–2625 (2005)
Brzeziński T., Caenepeel S., Militaru G.: Doi-Koppinen modules for quantum groupoids. J. Pure Appl. Algebra 175, 45–62 (2002)
Brzeziński T., Majid S.: Coalgebra bundles. Commun. Math. Phys. 191, 467–492 (1998)
Brzeziński T., Militaru G.: Bialgebroids, × a -bialgebras and duality. J. Algebra 251, 279–294 (2002)
Burghelea D.: The cyclic homology of the group rings. Comment. Math. Helv. 60, 354–365 (1985)
Burroni, E.: Algébres non déterministiques et D-catégories. Cahiers de Topologie et Géometrie Différentielle 14, 417–475, 480–481 (1973)
Caenepeel S., De Groot E.: Galois theory for weak Hopf algebras. Rev. Roumaine Math. Pures Appl. 52, 51–76 (2007)
Connes A., Moscovici H.: Local index formula in noncommutative geometry. Geom. Funct. Anal. 5, 174–243 (1995)
Connes A., Moscovici H.: Hopf algebras, cyclic cohomology and the transverse index theorem. Commun. Math. Phys. 198, 199–246 (1998)
Connes, A., Moscovici, H.: Differential cyclic cohomology and Hopf algebraic structures in transverse geometry. In: Essays on geometry and related topics. Vol. 1-2, Monogr. Enseign. Math. 38, Geneva: Enseignement Math., 2001, pp. 217–255
Crainic M.: Cyclic cohomology of étale groupoids: the general case. K-Theory 17, 319–362 (1999)
Eilenberg S., Moore J.C.: Adjoint functors and triples. Ill. J. Math. 9, 381–398 (1965)
Godement R.: Théorie des faisceaux. Hermann, Paris (1957)
Hajac P.M., Khalkhali M., Rangipour B., Sommerhäuser Y.: Stable anti-Yetter-Drinfeld modules. C. R. Math. Acad. Sci. Paris 338, 587–590 (2004)
Hajac P.M., Khalkhali M., Rangipour B., Sommerhäuser Y.: Hopf-cyclic homology and cohomology with coefficients. C. R. Math. Acad. Sci. Paris 338, 667–672 (2004)
Hobst, D.: Antipodes in the theory of noncommutative torsors. PhD thesis, Ludwig-Maximilians Universität München, 2004, Berlin: Logos Verlag, 2004
Jara P., Ştefan D.: Hopf-cyclic homology and relative cyclic homology of Hopf-Galois extensions. Proc. London Math. Soc. (3) 93, 138–174 (2006)
Kadison, L.: Cyclic homology of triangular matrix algebras, In: Topology Hawaii (Honolulu, HI, 1990), Singapore: World Sci., 1992
Kadison L., Szlachányi K.: Bialgebroid actions on depth two extensions and duality. Adv. Math. 179, 75–121 (2003)
Kasangian S., Lack S., Vitale E.: Coalgebras, braidings, and distributive laws. Theory and Applications of Categories 13, 129–146 (2004)
Kassel C.: Quantum groups, Graduate Text in Mathematics 155. Springer, Berlin-Heidelberg-New York (1995)
Kaygun A.: Bialgebra cyclic homology with coefficients. K-Theory 34, 151–194 (2005)
Kaygun, A.: The universal Hopf cyclic theory. To appear in J. Noncommut. Geom., available at http://arxiv.org/list/math/0609311
Khalkhali M., Rangipour B.: Invariant cyclic homology. K-Theory 28, 183–205 (2003)
Khalkhali M., Rangipour B.: Para-Hopf algebroids and their cyclic cohomology. Lett. Math. Phys. 70, 259–272 (2004)
Khalkhali M., Rangipour B.: A note on cyclic duality and Hopf algebras. Comm. Algebra 33, 763–773 (2005)
Lopez J., Panaite F., van Oystaeyen F.: General twisting of algebras. Adv. Mathematics 212, 315–337 (2007)
Loday J.-L.: Cyclic Homology. Springer-Verlag, Berlin-Heidelberg-New York (1992)
Lu J.H.: Hopf algebroids and quantum groupoids. Int. J. Math. 7, 47–70 (1996)
Mac Lane S.: Categories for the working mathematician. Springer-Verlag, Berlin-Heidelberg-New York (1974)
Majid S.: Foundations of quantum group theory. Cambridge University Press, Cambridge (1995)
Rangipour, B.: Cyclic cohomology of corings. http://arxiv.org/list/math/0607248, 2006
Schauenburg P.: Bialgebras over noncommutative rings and a structure theorem for Hopf bimodules. Appl. Categorical Str. 6, 193–222 (1998)
Schauenburg, P.: Duals and doubles of quantum groupoids ( × R -Hopf algebras). In: Andruskiewitsch, N., Ferrer-Santos, W.R., Schneider, H.-J. (eds.), AMS Contemp. Math. 267, RI: Amer. Math. Soc., Providence 2000, pp. 273–293
Škoda, Z.: Cyclic structures for simplicial objects from comonads. http://arxiv.org/list/math/0412001, 2004
Takeuchi M.: Groups of algebras over \({A\otimes {\overline A}}\) . J. Math. Soc. Japan 90, 459–492 (1977)
Vecsernyés P.: Larson-Sweedler theorem and the role of grouplike elements in weak Hopf algebras. J. Algebra 270, 471–520 (2003)
Weibel, C.: An introduction to homological algebra.Cambridge Studies in Advanced Mathematics 38. Cambridge: Cambridge, University Press, 1994
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Connes
Rights and permissions
About this article
Cite this article
Böhm, G., Ştefan, D. (Co)cyclic (Co)homology of Bialgebroids: An Approach via (Co)monads. Commun. Math. Phys. 282, 239–286 (2008). https://doi.org/10.1007/s00220-008-0540-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-008-0540-3