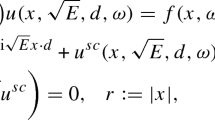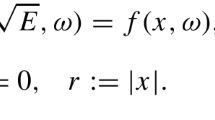Skip to main content
SpringerLink
Log in

Inverse Scattering Problem for a Two Dimensional Random Potential

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

We study an inverse problem for the two-dimensional random Schrödinger equation (Δ + q + k 2)u = 0. The potential q(x) is assumed to be a Gaussian random function whose covariance operator is a classical pseudodifferential operator. We show that the backscattered field, obtained from a single realization of the random potential q, determines uniquely the principal symbol of the covariance operator of q. The analysis is carried out by combining harmonic and microlocal analysis with stochastic methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abramowitz, M., Stegun, I.: Tables of Mathematical Functions. 9th print, New York: Dover, 1970

  2. Adler R. (1981). The Geometry of Random Fields. John Wiley & Sons, New York

    MATH  Google Scholar 

  3. Agmond S. (1975). Spectral properties of Schrödinger operators and scattering theory. Ann. Scuola norm. Sup. Pisa (4) 2: 151–218

    Google Scholar 

  4. Agranovsky M. and Quinto E. (1996). Injectivity sets for the Radon transform over circles and complete systems of radial functions. J. Funct. Anal. 139: 383–414

    Article  MATH  MathSciNet  Google Scholar 

  5. Astala K. and Päivärinta L. (2006). Uniqueness in Calderon’s inverse conductivity problem in the plane. Ann. Math. 163: 265–299

    Article  MATH  Google Scholar 

  6. Bal G., Papanicolaou G. and Ryzhik L. (2002). Radiative transport limit for the random Schrödinger equation. Nonlinearity 15: 513–529

    Article  MATH  ADS  MathSciNet  Google Scholar 

  7. Birman M.Sh. and Krein M.G. (1962). On the theory of wave operators and scattering operators. (Russian) Dokl. Akad. Nauk SSSR 144: 475–478

    MathSciNet  Google Scholar 

  8. Bogachev, V.: Gaussian measures. Mathematical Surveys and Monographs, 62. Providence, RI: Amer. Math. Soc., 1998

  9. Borcea L., Papanicolaou G., Tsogka C. and Berryman J. (2002). Imaging and time reversal in random media. Inverse Problems 18: 1247–1279

    Article  MATH  ADS  MathSciNet  Google Scholar 

  10. Bourgain J. and Kenig C.E. (2005). On localization in the continuous Andersson-Bernoulli model in higher dimension. Invent. Math. 161: 389–426

    Article  MATH  ADS  MathSciNet  Google Scholar 

  11. Brown R. and Uhlmann G. (1997). Uniqueness in the inverse conductivity problem for nonsmooth conductivities in two dimensions. Commun. Part. Diff. Eqs. 22(5–6): 1009–1027

    Article  MATH  MathSciNet  Google Scholar 

  12. Calderón, A.-P.: On an inverse boundary value problem. Seminar on Numerical Analysis and its Applications to Continuum Physics (Rio de Janeiro, 1980), Rio de Janeiro: Soc. Brasil. Mat., 1980, pp. 65–73

  13. Colton D. and Kress R. (1983). Integral Equation Methods in Scattering Theory. Pure and Applied Mathematics. John Wiley & Sons, New York

    Google Scholar 

  14. Cramer H. and Leadbetter M. (1967). Stationary and Related Stochastic Processes. John Wiley & Sons, New York

    MATH  Google Scholar 

  15. Eskin G. and Ralston J. (1989). The inverse backscattering problem in three dimensions. Commun. Math. Phys. 124: 169–215

    Article  MATH  ADS  MathSciNet  Google Scholar 

  16. Eskin G. and Ralston J. (1991). Inverse backscattering in two dimensions. Commun. Math. Phys. 138: 451–486

    Article  MATH  ADS  MathSciNet  Google Scholar 

  17. Fischer W., Leschke H. and Müller P. (2000). Spectral localization by Gaussian random potentials in multi-dimensional continuous space. J. Stat. Phys. 101: 935–985

    MATH  Google Scholar 

  18. Fröhlich J. and Spencer T. (1983). Absence of diffusion in the Anderson tight binding model for large disorder or low energy. Commun. Math. Phys. 88(2): 151–184

    Article  MATH  ADS  Google Scholar 

  19. Gel’fand I. and Vilenkin N. (1964). Generalized Functions. Vol. 1-4.. Academic Press, London-New York

    Google Scholar 

  20. Greenleaf A., Lassas M. and Uhlmann G. (2003). The Calderon problem for conormal potentials, I: Global uniqueness and reconstruction. Comm. Pure Appl. Math. 56: 328–352

    Article  MATH  MathSciNet  Google Scholar 

  21. Glimm J. and Jaffe A. (1971). The Yukawa quantum field theory without cutoffs. J. Funct. Anal. 7: 323–357

    Article  MathSciNet  Google Scholar 

  22. Hähner P. (1996). A periodic Faddeev-type solution operator. J. Differ. Eqs. 128(1): 300–308

    Article  MATH  Google Scholar 

  23. Hörmander L. (1985). The Analysis of Linear Partial Differential Operators. Vol. I.. Springer-Verlag, Berlin

    Google Scholar 

  24. Hörmander L. (1985). The Analysis of Linear Partial Differential Operators. Vol. III.. Springer-Verlag, Berlin

    Google Scholar 

  25. Jerison D. and Kenig K. (1985). Unique continuation and absence of positive eigenvalues for Schrödinger operators. Ann. Math. 121: 463–494

    Article  MathSciNet  Google Scholar 

  26. Kahane J.-P. (1985). Some Random Series of Functions.. Cambridge Univ. Press, Cambridge

    Google Scholar 

  27. Kenig C., Ruiz A. and Sogge C. (1987). Uniform Sobolev Inequalities and Unique continuation for second order constant coefficients differential operators. Duke Math. J. 55: 329–347

    Article  MATH  MathSciNet  Google Scholar 

  28. Koch H. and Tataru D. (2001). Carleman estimates and unique continuation for second order elliptic equations with nonsmooth coefficients. Commun. Math. Pure Appl. 54: 339–360

    Article  MATH  MathSciNet  Google Scholar 

  29. Kotani, S.: Lyapunov exponents and spectra for one-dimensional random Schrödinger operators. Random Matrices and Their Applications (Brunswick, Maine, 1984), Contemp. Math. 50, Providence, RI: Amer. Math. Soc., 1986, pp. 277–286

  30. Kotani S. and Simon B. (1987). Localization in general one-dimensional random systems. II. Continuum Schrödinger operators. Commun. Math. Phys. 112: 103–119

    Article  MATH  ADS  MathSciNet  Google Scholar 

  31. Lassas, M., Päivärinta, L., Saksman, E.: Inverse problem for a random potential. In: Partial Differential Equations and Inverse Problemsx, Contemp. Math. 362 Providence, RI: Amer. Math. Soc., 2004, pp. 277–288

  32. Ledoux M. and Talagrand M. (1991). Probability in Banach Spaces. Springer, Berlin-Heidelberg-New York

    MATH  Google Scholar 

  33. Lehtinen M., Päivärinta L. and Somersalo E. (1989). Linear inverse problems for generalised random variables. Inverse Problems 5: 599–612

    Article  MATH  ADS  MathSciNet  Google Scholar 

  34. Nachman A. (1988). Reconstructions from boundary measurements. Ann. Math. 128: 531–576

    Article  MathSciNet  Google Scholar 

  35. Nachman A. (1996). Global uniqueness for a two-dimensional inverse boundary value problem. Ann. Math. (2) 143(1): 71–96

    Article  MATH  MathSciNet  Google Scholar 

  36. Nachman A. and Sylvester, J., Uhlmann G. (1988). An n-dimensional Borg-Levinson theorem. Commun. Math. Phys. 115(4): 595–605

    Article  MATH  ADS  MathSciNet  Google Scholar 

  37. Neimam-Zade M. and Shkalikov A. (1999). The Schrödinger operators with singular potentials from the multiplicator’s spaces. (Russian) Matem. Zametki 66: 723–733

    Google Scholar 

  38. Ola P., Päivärinta L. and Serov V. (2001). Recovering singularities from backscattering in two dimensions. Comm. Partial Differ. Eqs. 26: 697–715

    Article  MATH  Google Scholar 

  39. Päivärinta, L.: Analytic methods for inverse scattering theory. In: New Analytic and Geometric Methods in Inverse Problems. Springer Lecture Notes Ed. Bingham, K., Kurylev, Y., Somersalo, E., Berline-Heidelberg New York: Springer, 2003, pp. 165–185

  40. Päivärinta L., Panchenko A. and Uhlmann G. (2003). Complex geometrical optics solutions for Lipschitz conductivities. Rev. Mat. Iberoamericana 19: 57–72

    MATH  MathSciNet  Google Scholar 

  41. Päivärinta L. and Serov V. (2002). An n-dimensional Borg-Levinson theorem for singular potentials. Adv. in Appl. Math. 29(4): 509–520

    Article  MATH  MathSciNet  Google Scholar 

  42. Päivärinta, L., Somersalo, E. (eds.): Inverse Problems in Mathematical Physics. Lecture Notes in Physics, 422. Berlin: Springer-Verlag, 1993

  43. Papanicolaou G., Postel M. and White B. (1991). Frequency content of randomly scattered signals. Siam Review 33: 519–626

    Article  MATH  MathSciNet  Google Scholar 

  44. Papanicolaou G. and Weinryb S. (1994). A functional limit theorem for waves reflected by a random medium. Appl. Math. Optim. 30: 307–334

    Article  MATH  MathSciNet  Google Scholar 

  45. Pastur L. (1980). Spectral properties of disordered systems in the one-body approximation. Commun. Math. Phys. 75: 179–196

    Article  MATH  ADS  MathSciNet  Google Scholar 

  46. Peetre J. (1960). Rectification à l’article Une charactérization abstraite des opérateurs differentiels. Math. Scand. 8: 116–120

    MATH  MathSciNet  Google Scholar 

  47. Rozanov Y. (1982). Markov Random Fields. Applications of Mathematics. Springer-Verlag, Berlin-Heidelberg-New York

    Google Scholar 

  48. Simon B. (1985). Localization in general one-dimensional random systems. I. Jacobi matrices. Commun. Math. Phys. 102: 327–336

    Article  MATH  ADS  Google Scholar 

  49. Simon B. and Wolff T. (1986). Singular continuous spectrum under rank one perturbations and localization for random Hamiltonians. Comm. Pure Appl. Math. 39(1): 75–90

    Article  MATH  MathSciNet  Google Scholar 

  50. Stefanov P. (1992). Generic uniqueness for two inverse problems in potential scattering. Comm. Partial Differ. Eqs. 17: 55–68

    Article  MathSciNet  MATH  Google Scholar 

  51. Stein E.M. (1993). Harmonic Analysis. Princeton University Press, Princeton, NJ

    MATH  Google Scholar 

  52. Sylvester J. and Uhlmann G. (1987). A global uniqueness theorem for an inverse boundary value problem. Ann. Math. 125(1): 153–169

    Article  MathSciNet  Google Scholar 

  53. Taylor, M. E.: Tools for PDE. Pseudodifferential Operators, Paradifferential Operators, and Layer Potentials. Mathematical Surveys and Monographs 81, Providence, RI: Amer. Math. Soc., 2000

  54. Ueki N. (2004). Wegner estimates and localization for Gaussian random potentials. Publ. Res. Inst. Math. Sci. 40(1): 29–90

    Article  MATH  MathSciNet  Google Scholar 

  55. Uhlmann, G.: Inverse boundary value problems for partial differential equations. Proceedings of the ICM. Vol. III (Berlin, 1998). Doc. Math. J. DMV Extra Vol. III, pp. 77–86 (1998)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Helsinki University of Technology, P.O.Box 1100, 02015, TKK, Finland

    Matti Lassas

  2. Department of Mathematics and Statistics, University of Helsinki, P.O.Box 68, 00014, Helsinki, Finland

    Lassi Päivärinta & Eero Saksman

Authors
  1. Matti Lassas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lassi Päivärinta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Eero Saksman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Matti Lassas.

Additional information

Communicated by B. Simon.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lassas, M., Päivärinta, L. & Saksman, E. Inverse Scattering Problem for a Two Dimensional Random Potential. Commun. Math. Phys. 279, 669–703 (2008). https://doi.org/10.1007/s00220-008-0416-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-008-0416-6

Keywords

Search

Navigation