Abstract
This paper is the first input towards an open analogue of the quantum Kirwan map. We consider the adiabatic limit of the symplectic vortex equation over the unit disk for a Hamiltonian G-manifold with Lagrangian boundary condition, by blowing up the metric on the disk. We define an appropriate notion of stable solutions in the limit, and prove that any sequence of disk vortices with energy uniformly bounded has a subsequence converging to such a stable object. We also proved several analytical properties of vortices over the upper half plane, which are new type of bubbles appearing in our compactification.
Similar content being viewed by others
Notes
Their works are for different coefficients.
Indeed, the constant \(\updelta \) can be taken to be any number smaller than 2. However, in this paper, we do not need the optimal result whose proof is more delicate.
References
Auroux, D.: Special Lagrangian fibrations, wall-crossing, and mirror symmetry. In: Geometry, Analysis, and Algebraic Geometry: Forty Years of the Journal of Differential Geometry, Surveys in Differential Geometry, vol. 13. International Press, Somerville, MA (2009)
Candelas, P., de la Ossa, X., Green, P., Parkes, L.: A pair of Calabi–Yau manifolds as an exactly soluble superconformal theory. Nucl. Phys. B 359, 21–74 (1991)
Chan, K., Lau, S.-C., Leung, N., Tseng, H.-H.: Open Gromov–Witten invariants, mirror maps, and Seidel representations for toric manifolds, arXiv:1209.6119 [math.SG], originally arXiv:1112.0388 [math.SG]
Charest, F., Woodward, C.: Floer trajectories and stabilizing divisors. arXiv:1401.0150 [math.SG]
Charest, F., Woodward, C.: Fukaya algebras via stabilizing divisors. arXiv:1505.08146 [math.SG]
Cho, C.-H.: Products of Floer cohomology of torus fibres in toric Fano manifolds. Commun. Math. Phys. 260(3), 613–640 (2005)
Cho, C.-H., Oh, Y.-G.: Floer cohomology and disk instantons of Lagrangian torus fibres in Fano toric manifolds. Asian J. Math. 10, 773–814 (2006)
Cieliebak, K., Gaio, A., Mundet, I., Salamon, D.: The symplectic vortex equations and invariants of Hamiltonian group actions. J. Symplectic Geom. 1(3), 543–645 (2002)
Cieliebak, K., Gaio, A., Salamon, D.: \({J}\)-holomorphic curves, moment maps, and invariants of Hamiltonian group actions. Int. Math. Res. Not. 16, 831–882 (2000)
Cieliebak, K., Mohnke, K.: Symplectic hypersurfaces and transversality in Gromov–Witten theory. J. Symplectic Geom. 5, 281–356 (2007)
Frauenfelder, U.: Floer Homology of Symplectic Quotients and the Arnold-Givental Conjecture, Ph.D. thesis, Swiss Federal Institute of Technology (2004)
Frauenfelder, U.: Gromov convergence of pseudoholomorphic disks. J. Fixed Point Theory Appl. 3, 215–271 (2008)
Fukaya, K., Oh, Y.-G.: Zero-loop open strings in the cotangent bundle and Morse homotopy. Asian J. Math. 1(1), 96–180 (1997)
Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Lagrangian Floer theory and mirror symmetry on compact toric manifolds. arXiv:1009.1648 [math.SG]
Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Lagrangian intersection Floer theory: anomaly and obstruction, part i & ii, AMS/IP studies in advanced mathematics, vol. 46, American Mathematical Society (2009)
Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Lagrangian Floer theory on compact toric manifolds, I. Duke Math. J. 151, 23–175 (2010)
Gaio, A., Salamon, D.: Gromov–Witten invariants of symplectic quotients and adiabatic limits. J. Symplectic Geom. 3(1), 55–159 (2005)
Givental, A.: Homological geometry and mirror symmetry. In: Proceedings of the International Congress of Mathematicians, vol. 1, 2 (Zürich, 1994), Birkhäuer, (1995), pp. 472–480
Givental, A.: Equivariant Gromov–Witten invariants. Int. Math. Res. Not. 1996, 613–663 (1996)
González, E., Woodward, C.: Quantum cohomology and toric minimal model program. arXiv:1207.3253 [math.AG]
González, E., Woodward, C.: Quantum Witten localization and abelianization for qde solutions. arXiv:0811.3358 [math.SG]
Hori, K., Vafa, C.: Mirror symmetry. arXiv:hep-th/0002222 (2000)
Ivashkovich, S., Shevchishin, V.: Reflection principle and J-complex curves with boundary on totally real immersions. Commun. Contemp. Math. 4(1), 65–106 (2002)
Lian, B., Liu, K., Yau, S.-T.: Mirror principle I. Asian J. Math. 1(4), 729–763 (1997)
McDuff, D., Salamon, D.: J-holomorphic curves and symplectic topology, Colloquium Publications, vol. 52, American Mathematical Society (2004)
Mundet, I.: Yang -Mills -Higgs Theory for Symplectic Fibrations, Ph.D. thesis, Universidad Autönoma de Madrid (1999)
Mundet, I.: Hamiltonian Gromov -Witten invariants. Topology 43(3), 525–553 (2003)
Mundet, I., Tian, G.: Hamiltonian Gromov -Witten invariants and Hamiltonian quantum product (in preparation)
Mundet, I., Tian, G.: A compactification of the moduli space of twisted holomorphic maps. Adv. Math. 222, 1117–1196 (2009)
Ott, A.: Removal of singularities and Gromov compactness for symplectic vortices. J. Symplectic Geom. 12(2), 257–311 (2014)
Poźniak, M.: Floer Homology, Novikov Rings and Clean Intersections, Ph.D. thesis, University of Warwick (1994)
Salamon, D.: Lectures on Floer homology. In: Eliashberg, Y., Traynor, L. (eds.) Symplectic Geometry and Topology, IAS/Park City Mathematics Series, vol. 7, American Mathematical Society, Providence, RI, pp. 143–229 (1997)
Venugopalan, S.: Vortices on surfaces with cylindrical ends. arXiv:1312.1074 [math.SG]
Venugopalan, S., Xu, G.: Local model for the moduli space of affine vortices. arXiv:1512.06713 [math.SG]
Wehrheim, K.: Uhlenbeck compactness. European Mathematical Society series of lectures in mathematics, European Mathematical Society (2003)
Woodward, C.: Gauged Floer theory for toric moment fibers. Geom. Funct. Anal. 21, 680–749 (2011)
Woodward, C.: Quantum Kirwan morphism and Gromov–Witten invariants of quotients I, II, III. Transform. Groups 20, 507–556, 881–920, 1155–1193 (2015)
Woodward, C., Xu, G.: Open quantum Kirwan map (in preparation)
Xu, G.: Gluing affine vortices. arXiv:1610.09764 [math.SG]
Xu, G.: Moduli space of twisted holomorphic maps with lagrangian boundary condition: compactness. Adv. Math. 242, 1–49 (2013)
Ziltener, F.: Symplectic Vortices on the Complex Plane and Quantum Cohomology, Ph.D. thesis, Swiss Federal Institute of Technology Zurich (2005)
Ziltener, F.: The invariant symplectic action and decay for vortices. J. Symplectic Geom. 7(3), 357–376 (2009)
Ziltener, F.: A quantum Kirwan map: bubbling and Fredholm theory. Mem. Am. Math. Soc. 230(1082), 1–129 (2014)
Acknowledgements
We are very grateful to Chris Woodward for suggesting this problem, sharing many ideas and for his hospitality during our visits to Rutgers University. We would like to thank Prof. Yong-Geun Oh and Prof. Gang Tian for helpful discussions. G.X. would like to thank Institute for Basic Science (Pohang) and Institute for Advanced Study (Princeton) for hospitality and would like to thank Nick Sheridan for helpful discussion.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Analysis of vortices
In this appendix we establish several necessary estimates related to the problem and provide proofs of Theorem 14 and Theorem 16. The techniques used here are standard, and all results which don’t involve boundary conditions are essentially covered in the previous literature such as [8] and [17]. A new technical result here is the proof of the existence of admissible almost complex structures with respect to a G-Lagrangian (Lemma 49).
1.1 Preliminaries
1.1.1 A neighborhood of \(\mu ^{-1}(0)\)
We assumed that 0 is a regular value of \(\mu \). Therefore we can fix two numbers \(\updelta >0\), \({\varvec{m}} = {\varvec{m}}(\updelta )>0\) satisfying that for any \(x \in X\) with \(|\mu (u)|\le \updelta \), the map  is injective and
is injective and

We fix these two numbers throughout this appendix.
1.1.2 G-invariant metrics
Let h be a G-invariant Riemannian metric on X with respect to which J is isometric. We denote by \(\nabla \) the Levi-Civita connection of h, and R the Riemannian curvature.
Let \(\Xi \subset {\mathbb H}\) be an open subset with coordinates (s, t). For any smooth map \((u, \phi , \psi ): \Xi \rightarrow X \times {\mathfrak g} \times {\mathfrak g}\), we denote

Moreover, we have a natural covariant derivative on \(u^* TX \oplus {\mathfrak g}\) associated with \((u, \phi , \psi )\), defined as follows. For any \(V \in \varGamma (u^* TX)\), we define

for \(\xi : \Xi \rightarrow {\mathfrak g}\), we define
By the G-invariance of h one can check that this covariant derivative preserves the metric.
We can extend the covariant derivative to tensor fields along u, by Leibniz rule. We denote  ,
,  . Then we have
. Then we have
Lemma 47
If T is a G-invariant tensor field on X and \(\nabla \) is the Levi-Civita connection of a G-invariant metric, then \(\nabla _{A, s} T = \nabla _{v_s} T\). In particular, if J is a G-invariant almost complex structure, then \(\nabla _{A, s}J = \nabla _{v_s} J\).
It is straightforward to extend the above result to \({\mathfrak g}\)-valued tensor fields. We denote
To estimate the energy density, it is convenient to have a special type of metrics on X.
Definition 48
Let L be a G-Lagrangian of \((X, \omega , \mu )\). Let J be a G-invariant almost complex structure. A \((J, L, \mu )\)-admissible Riemannian metric is a G-invariant Riemannian metric h on X satisfying
-
1.
J is isometric;
-
2.
J(TL) and TL are orthogonal with respect to h;
-
3.
L is totally geodesic with respect to h;
-
4.
\(T\mu ^{-1}(0)\) is orthogonal to
 for all \(\xi \in {\mathfrak g}\).
for all \(\xi \in {\mathfrak g}\).
In the non-equivariant case Frauenfelder [12] proved the existence of a similar type of metric for a Lagrangian submanifold satisfying (1)–(3). Here we generalize this result.
Lemma 49
For any G-Lagrangian L, and G-invariant almost complex structure J, there exists a \((J, L, \mu )\)-admissible Riemannian metric.
Proof
By [12, Lemma A.3], there exists a Riemannian metric \(\bar{h}\) on the symplectic quotient \(\bar{X}\) satisfying (1)–(3) for the Lagrangian \(\bar{L}\). Now we construct a suitable lift of \(\bar{h}\) to \(\mu ^{-1}(0)\). Let \(h_0\) be the metric on X induced by \(\omega \) and J. Let \(H\subset T\mu ^{-1}(0)\) be the orthogonal complement (with respect to \(h_0\)) of the distribution \(T{\mathfrak g}\) generated by infinitesimal G-actions. Then it is easy to see that H is G-invariant, and we have an isomorphism \(H \simeq \pi ^* T\bar{X}\), where \(\pi : \mu ^{-1}(0) \rightarrow \bar{X}\) is the projection. Then we can pull-back \(\bar{h}\) to a G-invariant metric on H, and choose a G-invariant metric on \(T{\mathfrak g}\) such that  . Let \(h'\) be the direct sum of the two components, which is a Riemannian metric on \(\mu ^{-1}(0)\).
. Let \(h'\) be the direct sum of the two components, which is a Riemannian metric on \(\mu ^{-1}(0)\).
We claim that L is totally geodesic in \(\mu ^{-1}(0)\) with respect to \(h'\). Let \(\nabla '\) be the Levi-Civita connection of \(h'\). It suffices to check that \((\nabla ')_X Y \in TL\) for any vector fields X, Y tangent to L. Since this is a pointwise condition, we assume that X, Y are both G-invariant. For any Z orthogonal to TL in \(\mu ^{-1}(0)\), we have (the inner products in the following are the ones for \(h'\))
We choose Z to be pull-backed from \(\bar{X}\) so that Z is G-invariant and \(\pi _* Z\) is a smooth vector field on \(\bar{X}\) and orthogonal to \(T\bar{L}\).
If \(X, Y \in \varGamma (H \cap TL) \simeq \varGamma (\pi ^* T\bar{L})\), then we choose X, Y to be pull-backed from \(\bar{X}\) and such that \(\langle X, Y \rangle \) is a constant. Then \(\pi _* X, \pi _* Y\) are smooth vector fields on \(\bar{X}\). Then by the definition of \(h'\), we see that
Then by the same calculation as (7.3), we know that the sum of the above two terms is equal to \(2\langle \bar{\nabla }_{\pi _* X} (\pi _* Y), \pi _* Z \rangle _{\bar{h}}\), which vanishes by the totally geodesic assumption on \(\bar{h}\).
On the other hand, if \(X \in \varGamma ( T{\mathfrak g})\) and \(Y\in \varGamma (H \cap TL)\), then \(\langle Y, X\rangle \equiv 0\). We can choose Z being G-invariant and [Y, Z] vanishing at a point where we want to evaluate (7.3). Then (7.3) vanishes at that point. Finally, if \(X, Y \in \varGamma (T{\mathfrak g})\), then we take  ,
,  for \(\xi , \eta \) constants. Then \(\langle Y, X \rangle \) is a constant and \([X, Z] = [Y, Z]= 0\). So (7.3) vanishes.
for \(\xi , \eta \) constants. Then \(\langle Y, X \rangle \) is a constant and \([X, Z] = [Y, Z]= 0\). So (7.3) vanishes.
Now we would like to extend \(h'\) to a metric on X which satisfies (1)–(4).
We choose local coordinates \(\theta _1, \ldots , \theta _k,x_1, \ldots , x_m\) of L where the first \(k = \mathrm{dim} G\) coordinates are coordinates of G-orbits. Extend them to coordinates
on X such that the first k coordinates are still coordinates of G-orbits, L is parametrized by \((\theta , x, 0, 0)\) and satisfying
on L. We remark that \(\frac{\partial }{\partial y_j}\) may not be tangent to \(\mu ^{-1}(0)\) but \(\mu ^{-1}(0)\) can be parametrized as \(( \theta , x, \tau (\theta , x, y), y)\) where \(\tau \) satisfies \(\tau (\theta , x, 0) = 0\). We write J as
where A, B, C, D are of size \((m+k) \times (m+k)\) and \(A(\theta , x, 0, 0) = D(\theta , x, 0, 0) = 0\), \(C(\theta , x, 0, 0) = - B(\theta , x, 0, 0)^T = I_{m+k}\). We consider a locally defined metric
where the matrix decomposition is written with respect to the same coordinates. Then the value of \(\widetilde{a}(\theta , x, \tau (\theta , x, y), y)\) and part of \(\widetilde{b}(\theta , x, \tau (\theta , x, y), y)\) and \(\widetilde{c}(\theta , x, \tau (\theta , x, y), y)\) have been determined by the choice of \(h'\). Then we choose the undetermined part of \(\widetilde{h}|_{\mu ^{-1}(0)}\) such that  for any \(\xi \in {\mathfrak g}\) with respect to \(\widetilde{h}|_{\mu ^{-1}(0)}\) and such that
for any \(\xi \in {\mathfrak g}\) with respect to \(\widetilde{h}|_{\mu ^{-1}(0)}\) and such that  . Moreover, we require that the 1-jet of \(\widetilde{h}\) along L in the \(\tau \)-direction satisfy
. Moreover, we require that the 1-jet of \(\widetilde{h}\) along L in the \(\tau \)-direction satisfy
Since \(A|_L\equiv 0\), the left-hand-side of this equation is \(\partial _{\tau _i} \widetilde{a}(\theta , x, 0, 0)\) plus terms which don’t contain derivatives of \(\widetilde{a}\). Therefore (7.4) has a solution subordinate to all the constrains we have put on the 0-jet of \(\widetilde{h}\). This gives us a metric \(\widetilde{h}\) defined in the coordinate patch.
Now we define \(h(v, w) = \frac{1}{2} \big ( \widetilde{h}(v, w) + \widetilde{h}(Jv, Jw) \big )\) and we claim that h satisfies Definition 48 inside the coordinate patch we are considering, except for the G-invariance. As in [12], we can use such locally constructed metrics and a partition of unity to construct a global metric h, satisfying (1)–(4).
Indeed, the first condition is automatic. For the fourth condition, for \(Y \in T\mu ^{-1}(0)\) and  , decompose \(Y = Y_1 + Y_2\) where \(Y_1 \in H\) and
, decompose \(Y = Y_1 + Y_2\) where \(Y_1 \in H\) and  for some \(\eta \in {\mathfrak g}\). Then
for some \(\eta \in {\mathfrak g}\). Then  by the condition required for \(\widetilde{h}\). Therefore, J(TL) is orthogonal to TL.
by the condition required for \(\widetilde{h}\). Therefore, J(TL) is orthogonal to TL.
For the totally geodesic condition, we see that (7.4) implies that for X, Y tangent to L, \(\nabla _X Y \in T\mu ^{-1}(0)|_L\) where \(\nabla \) is the Levi-Civita connection of h. Moreover, by the condition that  along \(\mu ^{-1}(0)\), we see that \(h|_{\mu ^{-1}(0)} = \widetilde{h}|_{\mu ^{-1}(0)}\). Since L is totally geodesic with respect to \(\widetilde{h}|_{\mu ^{-1}(0)} = h'\), this implies that \(\nabla _X Y \in TL\) and L is totally geodesic in the local coordinate patch.
along \(\mu ^{-1}(0)\), we see that \(h|_{\mu ^{-1}(0)} = \widetilde{h}|_{\mu ^{-1}(0)}\). Since L is totally geodesic with respect to \(\widetilde{h}|_{\mu ^{-1}(0)} = h'\), this implies that \(\nabla _X Y \in TL\) and L is totally geodesic in the local coordinate patch.
Now the metric h constructed above may not be G-invariant. We integrate h against the Haar measure of G, getting a G-invariant metric \(\hat{h}\). The point-wise conditions (1), (2), (4) are clearly preserved. To see that L is totally geodesic with respect to \(\hat{h}\), it suffices to show that for any vector fields X, Y tangent to L, \(\hat{\nabla }_X Y\) is tangent to L, where \(\hat{\nabla }\) is the Levi-Civita connection of h. Indeed, if we denote by \(\nabla \) the Levi-Civita connection of h, then
Since L is G-invariant, \(g_* X\), \(g_* Y\) are both tangent to L. Therefore we see that \(\hat{\nabla }_X Y\) is tangent to L. Therefore \(\hat{h}\) is a \((J, L, \mu )\)-admissible metric. \(\square \)
Now we fix a \((J, L, \mu )\)-admissible metric h on X. We use \(\langle \cdot , \cdot \rangle \) to denote the inner product of h in the remaining of this appendix. Then by (4) of Definition 48, there exists \({\varvec{n}}= {\varvec{n}}(\updelta )>0\) such that for any \(x \in X\) with \(|\mu (x)| \le \updelta \), and any \(Y \in T_x X\),

Since a rescaling of h is still \((J, L, \mu )\)-admissible, we may assume instead

Moreover, we may assume that h coincides with a small constant multiple of \(\omega (\cdot , J \cdot )\) whenever \(|\mu (x)| \ge \updelta \), so that (7.5) holds throughout X.
1.2 The isoperimetric inequality
We first recall Poźniak’s isoperimetric inequality ([31, Lemma 3.4.5]). Let \((Y, \omega )\) be a symplectic manifold and let \(L_0, L_1\subset Y\) be two compact Lagrangian submanifolds which intersect cleanly in Y.
Lemma 50
[31, Lemma 3.4.5] There exist constants \(\updelta ' = \updelta '(L_0, L_1) >0\) and \({\varvec{c}}' = {\varvec{c}}'(L_0, L_1)>0\) satisfying the following condition. Let \(x: [0, \pi ] \rightarrow Y\) be a \(C^1\)-path with \(x(0) \in L_0, x(1) \in L_1\) and \(\int _0^\pi |x'(t)|^2 dt \le ( \updelta ')^2\). Then there exists a \(C^1\)-map \(v: [0,1]\times [0, \pi ] \rightarrow X\) with
Moreover, if we define the symplectic action of the path x as
then
Now we consider two G-Lagrangian submanifolds \(L_0, L_1\) of the Hamiltonian G-manifold \((X, \omega , \mu )\). Suppose they intersect cleanly in \(\bar{X}\). Consider the path spaces

Then we define a “local action functional” analogous to that in [11] and [17] when a path  is sufficiently close to
is sufficiently close to  . More precisely, for
. More precisely, for  , we denote
, we denote

Then we have
Lemma 51
There exist positive constants \(\updelta = \updelta (L_0, L_1)\) and \({\varvec{c}} = {\varvec{c}}(L_0, L_1)\) such that for  with
with

there exists  such that
such that
Proof
For small \(\updelta >0\), there exist a unique path \((x_0, \eta _0): [0,\pi ]\rightarrow \mu ^{-1}(0) \times {\mathfrak g}\) such that

Moreover, there exists \(c_2>0\) such that

On the other hand, since \(\bar{L}_0\) and \(\bar{L}_1\) intersect cleanly, there exists \(\bar{q} \in \bar{L}_0 \cap \bar{L}_1\) such that
Then we can choose a lift \(q \in L_0 \cap L_1\) of \(\bar{q}\), such that
On the other hand, choose \(g: [0,\pi ]\rightarrow G\) such that \(g(0) = \mathrm{Id}\), \( g'(t) g(t)^{-1} = -\eta (t)\). Define

Then we see there exists \(c_5>0\) such that
\(\square \)
For \(\updelta >0\), denote by  the subset of pairs \((x, \eta )\) that satisfy (7.8). Then we define the local action functional for all
the subset of pairs \((x, \eta )\) that satisfy (7.8). Then we define the local action functional for all  by
by

Lemma 52
There exist positive constants \(\updelta = \updelta (L_0, L_1)\) and \({\varvec{c}} = {\varvec{c}}(L_0, L_1)\) such that for  , we have
, we have

Proof
The same as in Step 3 of the proof of [11, Lemma 3.17]. \(\square \)
1.3 A priori estimates
Lemma 53
Let \(u: B_{R+r} \rightarrow {\mathbb R}_+\cup \{0\}\) be a \(C^2\)-function and \(a>0\) such that
Then for any \(x \in B_R\),
Proof
We first prove for the case that \(r = 1\). Using the Heinz trick (cf. [25, Page 82]), define the function \(f: [0, 1]\rightarrow {\mathbb R}\) by
Let \(\rho ^* \in [0,1)\) be some number at which f attains its maximum. Choose \(w^* \in B_{\rho ^*}(x)\) such that \(u(z^*) = \sup _{B_{\rho ^*}(x)} u\) and denote \(c^* = u(z^*)\). Denote \(\delta = \frac{1 - \rho ^* }{2}< 1\). Then for \(w \in B_\delta (w^*)\),
Therefore on \(B_\delta (w^*)\), we have
which implies that the function \(\widetilde{u}(w) = u(w) + m c^* |w- w^*|^2\) is subharmonic on \(B_\delta (w^*)\). Therefore, for any \(\rho \in (0, \delta ]\), we have
Now if \( m \delta ^2 \le 1\), then we take \(\rho = \delta \), which implies that
Then
On the other hand, if \(m \delta ^2 > 1\), then take \(\rho = \sqrt{ \frac{ 1 }{m } } < \delta \), we see
Therefore
It implies that \(c^* \le \frac{1}{4}\). Therefore
In summary, we see that
For general \(r>0\), the estimate follows by applying the above argument to \(v(x) = u(rx)\) and a replaced by \(ar^2\). \(\square \)
1.4 Mean-value estimate
Let h be a \((J, L, \mu )\)-admissible metric on X satisfying (7.5). Let \(\nabla \) be the Levi-Civita connection of h and we have the covariant derivatives defined by (7.2).
Now we consider the vortex equation on \(\Xi \). An area form can be written as \(\sigma ds dt\) for a smooth function \(\sigma : \Xi \rightarrow (0, +\infty )\). We assume that there exist \(c^{(l)} >0\), \(l = 1, \ldots \) such that
The vortex equation is written as
Using a G-invariant metric h, we define the energy density for a solution \((u, \phi , \psi )\) by
where second norm is the G-invariant metric on \({\mathfrak g}\) we used to define the vortex equation.
Lemma 54
Let \(\Xi \subset {\mathbb C}\) be an open subset. For any compact subset \(K\subset X\), there exists \({\varvec{c}} = {\varvec{c}}(K)>0\) depending on K (and also on the constants \(c^{(l)}\) of (7.9)) such that for any solution \((u, \phi , \psi )\) of (7.10) satisfying \(u(\Xi ) \subset K\), its energy density function e satisfies
Here \(\varDelta \) is the standard Laplacian in coordinates (s, t). If \(\sigma \) is constant, we have
Proof
Since the covariant derivative respects the metric, we have

Denote \(\bar{\rho }(v_s, v_t) = \rho (v_s, v_t) - \rho (v_t, v_s)\). Then there exist \(c_K>0\) and for any \(\epsilon >0\), \(c_{K, \epsilon }>0\), depending on the metric h and the compact subset K such that

To estimate \(\varDelta |v_s|^2\), we have the following standard calculations.



On the other hand, by the G-invariance of \(\nabla J\) and Lemma 47, there exist tensors \(L_1, L_2, L_3\) such that
Therefore, we have

Therefore, since \(u(\Xi )\subset K\), with abusive use of (small) \(\epsilon \) and (big) \(c_{K, \epsilon }\), we have

Therefore, by (7.9), (7.13) and (7.17), we have

Here the second inequality follows from (7.5). Moreover, if \(|\mu | \le \updelta \), then for \(\epsilon \le {\varvec{m}}\), the first term of the last line is nonnegative; if \(|\mu |> \updelta \), then the first term is greater than or equal to \(- \epsilon \updelta ^{-2} \sigma ^2 |\mu |^4\). In either case, there exist \({\varvec{c}}', {\varvec{c}}>0\) depending on \(c_{K, \epsilon }\), \({\varvec{m}}\), \({\varvec{n}}\) and \(\updelta \) such that

This implies (7.11). (7.12) follows by setting \(c^{(1)}= c^{(2)} = 0\). \(\square \)
1.5 Removal of singularity at punctures
We prove the first part of Lemma 8, which we restate as follows.
Proposition 55
Let \(L_-, L_+\) be two G-Lagrangians of X which intersect cleanly in \(\bar{X}\). Let \((\varSigma , \partial \varSigma ) = \left( {\mathbb D}^* \cap {\mathbb H}, {\mathbb D}^* \cap {\mathbb R} \right) \) and \(\partial _\pm \varSigma = {\mathbb D}^* \cap {\mathbb R}_\pm \). Suppose \(\mathbf{v}\) is a bounded solution to (2.2) on \(\left( \varSigma , \partial \varSigma \right) \) with respect to a smooth area form \(\nu \in \varOmega ^2 ( \varSigma )\). Then there exists a smooth gauge transformation \(g: \varSigma \rightarrow G\) such that \(g^* u\) extends continuously to \(\{0\}\).
Proof
Identify \(\varSigma \) with \([0, +\infty ) \times [0, \pi ]\) via \(\varSigma \ni z \mapsto w = s + {\varvec{i}} t= - \log z\) and view the strip as a subset of \({\mathbb H}\). Suppose \(\nu = \sigma ds dt\), it is easy to check that (7.9) is satisfied. Let \(\widetilde{e}: [0, +\infty ) \times [0,\pi ] \rightarrow {\mathbb R}_+ \cup \{0\}\) be the energy density function. By Lemma 54, we have
Here \({\varvec{c}}\) depends on a choice of G-invariant metric on X.
Now to derive pointwise decay of \(\widetilde{e}\) as \(s \rightarrow +\infty \), we have to extend \(\widetilde{e}\) a bit beyond the boundary of \([0,+\infty ) \times [0,\pi ]\). For example, we use reflection to define
for \(a > 0\) a small constant. Then \(\widetilde{e}\) is extended to \([0, +\infty ) \times (-a, 1]\). To see that the extension still satisfies (7.11), it suffices to show that \(\partial _t \widetilde{e}(s, 0) = 0\). This is the place where we need the properties of metrics defined by Definition 48. Choose a \((J, L_-, \mu )\)-admissible metric \(h_-\).
First, by the boundary condition, \(\partial _t | \mu (u) |^2 = 0\). On the other hand,

Here the third equality follows from (7.14) and the last follows from \(\nabla _{A, s} J = \nabla _{v_s} J\). Then evaluating at \(t = 0\), we see that in the last row, the first term vanishes because \(\nabla J\) is skew-adjoint; the second term vanishes because \(L_-\) is totally geodesic and \(JTL_-\) is orthogonal to \(TL_-\); the third term vanishes by the boundary condition.
Therefore (7.11) holds on \([0, +\infty ) \times (-a, 1]\), for the constant \({\varvec{c}}\) associated with the metric \(h_-\). By the mean value estimate ([32, Page 12]) for any \(B_{\frac{a}{2}}(w) \subset [0, +\infty ) \times (-a, \pi ]\),
To achieve the estimate near the other boundary component, simply take a \((J, L_+, \mu )\)-admissible metric \(h_+\) and do the reflection along the other boundary. Since all metrics are equivalent, we see that \(\widetilde{e}(s, t)\) converges to zero uniformly as \(s \rightarrow +\infty \).
On the other hand, it is easy to see that there exists a gauge transformation \(g: [0, +\infty ) \times [0,1] \rightarrow G\) which transforms (A, u) into temporal gauge, i.e.,
Since \(\sigma \) decays exponentially as \(s \rightarrow +\infty \), by the equation \(\partial _s \psi + \sigma \mu (u) = 0\) and the uniform boundedness of \(|\mu (u)|\), we see that

Therefore \(\left| \partial _t u (s, t) \right| \rightarrow 0\) as \(s \rightarrow +\infty \). Let \(\gamma _s(t) = u(s, t)\). Since \(L_-\) and \(L_+\) intersect cleanly in X, by the Poźniak’s isoperimetric inequality Lemma 50, we can prove that there exists \(x\in L_- \cap L_+\) such that \(\lim _{s \rightarrow \infty } u(s, t) = x\). \(\square \)
1.6 Energy quantization of \({\mathbb H}\)-vortices
Proposition 56
Let L be a G-Lagrangian of X and \(K \subset X\) be a compact subset. Then there exists a constant \(\epsilon _{K, L} > 0\) such that the following holds. Suppose \(z_0 \in {\mathbb H}\) and \(r>0\). Suppose  . Then if \(u( B_{2r}(z_0) \cap {\mathbb H})\subset K\) and \(E(\mathbf{v}) < \epsilon _{K, L}\), then
. Then if \(u( B_{2r}(z_0) \cap {\mathbb H})\subset K\) and \(E(\mathbf{v}) < \epsilon _{K, L}\), then
Here \(e(\mathbf{v}): B_{2r}(z_0) \cap {\mathbb H} \rightarrow {\mathbb R}_+ \cup \{0\}\) is the energy density function of \(\mathbf{v}\) with respect to the standard metric on \({\mathbb H}\) and a \((J, L, \mu )\)-admissible metric h.
Proof
For the same reason as in the proof of Proposition 55, e can be extended to \(B_{2r}(z_0) \subset {\mathbb C}\) by reflection along the boundary of \(B_{2r}(z_0) \cap {\mathbb H}\). This extension still satisfies
Then by [25, Lemma 4.3.2], the estimate holds. \(\square \)
Proof (Proof of Theorem 16)
Choose \(\epsilon _{X, L} = \epsilon _{K, L}\) for \(K = X_{c_0}\) where \(X_{c_0}\) is the one in (2.3). Suppose \(\mathbf{v}\) is an \({\mathbb H}\)-vortex and \(E(\mathbf{v}) < \epsilon _{X, L}\). Then by the mean value estimate in Proposition 56, we see that for any \(z\in {\mathbb H}\) and \( r>0\),
Let \(r\rightarrow \infty \), we have \(e(z)=0\). Thus \(E(\mathbf{v})=0\). \(\square \)
1.7 Annulus lemma for vortices on strips
Ziltener proved ([43, Proposition 45]) that for any annulus \(A(r, R) = \{z\in {\mathbb C}\ |\ r\le |z|\le R\}\) and any small \(\epsilon >0\), there exists a constant \(E(r, \epsilon )\) such that for any vortex \(\mathbf{v} = (A, u)\) on A(r, R) with respect to the standard area form, if \(E(\mathbf{v}) \le E(r, \epsilon )\), then
for some constant \(c>0\) and for any \(a \in \big [ 2, \sqrt{ R/r} \big ]\). Now we prove an analogue of this result on strips. Via the map \(w = s + {\varvec{i}}t = \log z\), we identify the strip \(A^+(r, R) = A(r, R) \cap {\mathbb H}\) with
Let \(\nu = \sigma (s, t) ds dt\) be an area form satisfying (7.9).
Proposition 57
There exists \({\varvec{a}} = {\varvec{a}}(L_-, L_+) > 0\), \(\upepsilon = \upepsilon (L_-, L_+)>0\) satisfying the following condition. Given a smooth solution \(\mathbf{v} = (u, \phi , \psi )\) to (7.10) with boundary condition \(u(A(r, R)\cap {\mathbb R}_\pm ) \subset L_\pm \). Suppose \(\sigma \) is bounded from below by a constant \(\underline{\sigma }\). If \(E(\mathbf{v}) \le \upepsilon \), then for any \(s \in \left[ \log 2, \frac{1}{2} ( q-p) \right] \), we have
Here \({\varvec{c}} = {\varvec{c}} (L_-, L_+) >0\) is the \({\varvec{c}}(L_0, L_1)\) in Lemma 52 for \(L_0 = L_+\), \(L_1 = L_-\).
Proof
Let \(\epsilon (s, t)\) be the energy density with respect to the cylindrical coordinates, so that
By the estimate of Lemma 54 on the strip and Lemma 53, we know that there exists \(\upepsilon >0\) such that if \(E (\mathbf{v}; A^+(r, R) ) \le \upepsilon \), then for any \((s, t) \in [ p + \log 2, q - \log 2] \times [0, \pi ]\), we have \(\epsilon (s, t)\le \updelta (L_-, L_+)\). Here \(\updelta (L_-, L_+)\) is the one from Lemma 52. (Notice that when applying Lemma 53, we have to use \((J, L_\pm , \mu )\)-admissible metrics to extend the energy density function beyond the boundary of the strip, and notice that the r of Lemma 53 is uniformly bounded). We write \(A = d + \phi (s, t) ds + \psi (s, t) dt\). Then for \(s \in [p + 2, q - 2]\), we have  . So we can define the local equivariant action
. So we can define the local equivariant action

For \(s \in [ \log 2, ( q - p)/2 ] \), we denote \(E(s) = E ( \mathbf{v}; A^+ ( e^s r, e^{-s} R) )\). Then by the isoperimetric inequality (Lemma 52), for \({\varvec{c}} = {\varvec{c}}(L_-, L_+)\), we have

Here \(e(s, t) = |v_t(s, t)|^2 + \sigma (s, t)|\mu (u(s, t))|^2\). Abbreviate \(\widetilde{\varvec{c}} = {\varvec{c}}/ \min \{1, \underline{\sigma }\}\). Then we have
Therefore (7.20) holds.
To prove the estimate for the radius, apply Lemma 53 to \(\epsilon \) again, for a choice of r uniformly bounded from below. Then e decays in a similar way as
Integrating over \([ p + s, q - s]\) gives the upper bound on the equivariant diameter. \(\square \)
Now we prove the following asymptotic property of \({\mathbb H}\)-vortices.
Proof (Proof of Theorem 14)
Let \(q \rightarrow +\infty \) in (7.22), we obtain
Since \(\epsilon (s, t) = e^{2s} e(s, t)\), we obtain (2.7). On the other hand, we could transform (A, u) into temporal gauge, i.e., \(A = d + \psi d t\) such that
Then the decay of \(\epsilon \) implies that in this gauge, u converges to a limit in \(L_- \cap L_+\). \(\square \)
Appendix 2: Trees
In this appendix we fix notions and notations of trees.
In our convention, a tree  consists of a finite set of vertices
consists of a finite set of vertices  , a finite set of (finite) edges
, a finite set of (finite) edges  , and a finite set of semi-infinite edges
, and a finite set of semi-infinite edges
 . The semi-infinite edges are attached to vertices, by a map
. The semi-infinite edges are attached to vertices, by a map  . A rooted tree is a tree with a distinguished vertex, which is usually denoted by \(v_\infty \).
. A rooted tree is a tree with a distinguished vertex, which is usually denoted by \(v_\infty \).
In this paper we mainly consider rooted trees. There are obvious notions of morphisms between rooted trees, and rooted subtrees. We index vertices by letters \(\alpha , \beta , \gamma \), etc.. For a rooted tree  , there is a canonical partial order \(\le \) in
, there is a canonical partial order \(\le \) in  with \(v_\infty \) the unique minimal element. Moreover, for notational purpose, we only consider edges with the correct orientation, i.e., for
with \(v_\infty \) the unique minimal element. Moreover, for notational purpose, we only consider edges with the correct orientation, i.e., for  , we write \(\alpha \succ \beta \) if and only if \(v_\alpha \), \(v_\beta \) are adjacent and \(\beta \le \alpha \). For any
, we write \(\alpha \succ \beta \) if and only if \(v_\alpha \), \(v_\beta \) are adjacent and \(\beta \le \alpha \). For any  , we denote by
, we denote by  the unique vertex such that
the unique vertex such that  . For
. For  , denote by
, denote by  the end point of \(e'\) which is closer to the root.
the end point of \(e'\) which is closer to the root.
We regard a tree  as a 1-dimensional simplicial complex. Note that a semi-infinite edge only has one end combinatorially, but the point at infinity on the semi-infinite edge is regarded as a point of the simplicial complex.
as a 1-dimensional simplicial complex. Note that a semi-infinite edge only has one end combinatorially, but the point at infinity on the semi-infinite edge is regarded as a point of the simplicial complex.
Definition 58
([13, Definition 1.1])
-
1.
A rooted ribbon tree with \(\underline{k}\) semi-infinite edges consists of a rooted tree
 with a topological embedding
with a topological embedding  such that
such that  consists of the \(\underline{k}\) infinities of these semi-infinite edges. As a convention we always order the semi-infinite edges by \(e_1, \ldots , e_{\underline{k}}\) which respects the cyclic ordering induced by the embedding.
consists of the \(\underline{k}\) infinities of these semi-infinite edges. As a convention we always order the semi-infinite edges by \(e_1, \ldots , e_{\underline{k}}\) which respects the cyclic ordering induced by the embedding. -
2.
An isomorphism between two rooted ribbon trees
 and
and  consists of a rooted tree isomorphism
consists of a rooted tree isomorphism  together with an isotopy
together with an isotopy  as embedding of pairs between \({\mathfrak i}'\circ \rho \) and \({\mathfrak i}\). Two ribbon trees with \(\underline{k}\) semi-infinite edges are equivalent if there is an isomorphism between them. An isotopy class of embeddings \({\mathfrak i}\) for a rooted tree
as embedding of pairs between \({\mathfrak i}'\circ \rho \) and \({\mathfrak i}\). Two ribbon trees with \(\underline{k}\) semi-infinite edges are equivalent if there is an isomorphism between them. An isotopy class of embeddings \({\mathfrak i}\) for a rooted tree  is called a ribbon structure on
is called a ribbon structure on  .
. -
3.
A based rooted tree consists of a rooted tree
 and a rooted subtree
and a rooted subtree  where the latter is equipped with a ribbon structure.
where the latter is equipped with a ribbon structure. -
4.
A colored rooted tree is a rooted tree
 together with an order-reversing map
together with an order-reversing map  (called the coloring) such that within every path of
(called the coloring) such that within every path of  , \({\mathfrak s}^{-1}(1)\) consists of at most one vertex.
, \({\mathfrak s}^{-1}(1)\) consists of at most one vertex. -
5.
A vertex \(v_\alpha \) of a based colored rooted tree
 is stable if one of the followings is true.
is stable if one of the followings is true.-
\(v_\alpha = v_\infty \);
-
 and
and  ;
; -
 and
and  ;
; -
 .
.
-
Definition 59
Let  be a based colored rooted tree. A growth is another based colored rooted tree
be a based colored rooted tree. A growth is another based colored rooted tree  with a morphism
with a morphism  , which is the composition of finitely many elementary growths of the following types.
, which is the composition of finitely many elementary growths of the following types.
 In this case
In this case  with
with  . \(\rho \) contracts the edge
. \(\rho \) contracts the edge  .
.  corresponds to sphere bubbling downstairs.
corresponds to sphere bubbling downstairs.
 In this case
In this case  with
with  . \(\rho \) contracts the edge
. \(\rho \) contracts the edge  .
.  corresponds to disk bubbling downstairs.
corresponds to disk bubbling downstairs.
 In this case
In this case  with
with  . \(\rho \) contracts the edge
. \(\rho \) contracts the edge  .
.  corresponds to the \({\mathbb C}\)-vortex bubbling.
corresponds to the \({\mathbb C}\)-vortex bubbling.
 In this case
In this case  with
with  . \(\rho \) contracts the edge \(e_{\underline{\alpha }\underline{\alpha }'}\).
. \(\rho \) contracts the edge \(e_{\underline{\alpha }\underline{\alpha }'}\).  corresponds to \({\mathbb H}\)-vortex bubbling.
corresponds to \({\mathbb H}\)-vortex bubbling.
 In this case
In this case  with
with  . \(\rho \) contracts the edge \(e_{\alpha \alpha '}\).
. \(\rho \) contracts the edge \(e_{\alpha \alpha '}\).  corresponds to sphere bubbling upstairs.
corresponds to sphere bubbling upstairs.
 In this case
In this case  with
with  . \(\rho \) contracts the edge \(e_{\underline{\alpha }\underline{\alpha }'}\).
. \(\rho \) contracts the edge \(e_{\underline{\alpha }\underline{\alpha }'}\).  corresponds to disk bubbling upstairs.
corresponds to disk bubbling upstairs.
 In this case
In this case  and \(\rho \) contracts the path \(\underline{\alpha }\succ \underline{\alpha }_1 \succ \cdots \succ \underline{\alpha }_s \succ \underline{\alpha }'\) in
and \(\rho \) contracts the path \(\underline{\alpha }\succ \underline{\alpha }_1 \succ \cdots \succ \underline{\alpha }_s \succ \underline{\alpha }'\) in  to the edge
to the edge  .
.  corresponds to the appearance of connecting disk bubbles, either upstairs or downstairs.
corresponds to the appearance of connecting disk bubbles, either upstairs or downstairs.
1.1 Combinatorial types of stable holomorphic spheres and disks
In this subsection we set up some convention of expressing holomorphic spheres or disks.
1.1.1 Holomorphic spheres
Stable holomorphic spheres are modelled on ordinary trees. We will consider stable holomorphic spheres with a single marked point, which specifies a root of the tree. Therefore, rooted trees are what such objects are modelled on. Let  be a rooted tree. A stable holomorphic sphere in an almost Kähler manifold \((X, \omega , J)\) modelled on
be a rooted tree. A stable holomorphic sphere in an almost Kähler manifold \((X, \omega , J)\) modelled on  is a collection of objects
is a collection of objects

where
-
1.
For each
 , \(u_\alpha : {\mathbb C} \rightarrow X\) is a holomorhpic map with finite energy (therefore extends to a holomorphic sphere with an evaluation \(u_\alpha (\infty )\)), such that \(E(u_\alpha ) = 0\) implies that
, \(u_\alpha : {\mathbb C} \rightarrow X\) is a holomorhpic map with finite energy (therefore extends to a holomorphic sphere with an evaluation \(u_\alpha (\infty )\)), such that \(E(u_\alpha ) = 0\) implies that  or \(v_\alpha = v_\infty \) and
or \(v_\alpha = v_\infty \) and  .
. -
2.
For each
 , \(z_{\alpha \beta } \in {\mathbb C}\) such that \(u_\alpha (\infty ) = u_\beta ( z_{\alpha \beta })\) and for each
, \(z_{\alpha \beta } \in {\mathbb C}\) such that \(u_\alpha (\infty ) = u_\beta ( z_{\alpha \beta })\) and for each  , the collection of points \(Z_\beta := ( z_{\alpha \beta } )_{\beta = \alpha '}\) are distinct.
, the collection of points \(Z_\beta := ( z_{\alpha \beta } )_{\beta = \alpha '}\) are distinct.
In this situation, we call the rooted tree  a branch.
a branch.
1.1.2 Holomorphic disks
Stable holomorphic disks are modelled on based trees. We will consider stable holomorphic disks with a single boundary marked point, which specifies a root of the base. A stable J-holomorphic disk in (X, L) modelled on a based rooted tree  is a collection
is a collection

where
-
1.
For each
 , \(u_{\underline{\alpha }}: ({\mathbb H}, {\mathbb R}) \rightarrow (X, L)\) is a holomorphic map with finite energy (therefore extends to a holomorphic disk in (X, L) with an evaluation \(u_{\underline{\alpha }}(\infty )\)); for each
, \(u_{\underline{\alpha }}: ({\mathbb H}, {\mathbb R}) \rightarrow (X, L)\) is a holomorphic map with finite energy (therefore extends to a holomorphic disk in (X, L) with an evaluation \(u_{\underline{\alpha }}(\infty )\)); for each  , \(u_\alpha : {\mathbb C} \rightarrow X\) is a holomorphic map with finite energy (therefore has an evaluation \(u_\alpha (\infty )\)); they should satisfy the stability condition: for
, \(u_\alpha : {\mathbb C} \rightarrow X\) is a holomorphic map with finite energy (therefore has an evaluation \(u_\alpha (\infty )\)); they should satisfy the stability condition: for  and \(E(u_\alpha ) = 0\),
and \(E(u_\alpha ) = 0\),  ; if
; if  and \(E(u_\alpha ) = 0\),
and \(E(u_\alpha ) = 0\),  ; if \(E(u_\infty ) = 0\) then
; if \(E(u_\infty ) = 0\) then  .
. -
2.
(Denote \(\varSigma _\alpha = {\mathbb H}\) if
 and \(\varSigma _\alpha = {\mathbb C}\) otherwise.) For each
and \(\varSigma _\alpha = {\mathbb C}\) otherwise.) For each  , \(z_{\alpha \beta }\in \partial \varSigma _\beta \); for each
, \(z_{\alpha \beta }\in \partial \varSigma _\beta \); for each  , \(z_{\alpha \beta }\in \mathrm{Int} \varSigma _\beta \). They satisfy \(u_\alpha (\infty ) = u_\beta ( z_{\alpha \beta })\) and for each
, \(z_{\alpha \beta }\in \mathrm{Int} \varSigma _\beta \). They satisfy \(u_\alpha (\infty ) = u_\beta ( z_{\alpha \beta })\) and for each  , the collection of points \(Z_\beta := (z_{\alpha \beta })_{\alpha ' = \beta }\) are distinct.
, the collection of points \(Z_\beta := (z_{\alpha \beta })_{\alpha ' = \beta }\) are distinct.
In this situation, we call the based rooted tree  a based branch.
a based branch.
Rights and permissions
About this article
Cite this article
Wang, D., Xu, G. Compactness in the adiabatic limit of disk vortices. Math. Z. 287, 405–459 (2017). https://doi.org/10.1007/s00209-016-1830-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-016-1830-7


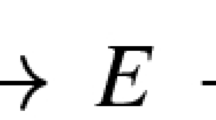


 for all
for all  with a topological embedding
with a topological embedding  such that
such that  consists of the
consists of the  and
and  consists of a rooted tree isomorphism
consists of a rooted tree isomorphism  together with an isotopy
together with an isotopy  as embedding of pairs between
as embedding of pairs between  is called a ribbon structure on
is called a ribbon structure on  .
. and a rooted subtree
and a rooted subtree  where the latter is equipped with a ribbon structure.
where the latter is equipped with a ribbon structure. together with an order-reversing map
together with an order-reversing map  (called the coloring) such that within every path of
(called the coloring) such that within every path of  ,
,  is stable if one of the followings is true.
is stable if one of the followings is true. and
and  ;
; and
and  ;
; .
. ,
,  or
or  .
. ,
,  , the collection of points
, the collection of points  ,
,  ,
,  and
and  ; if
; if  and
and  ; if
; if  .
. and
and  ,
,  ,
,  , the collection of points
, the collection of points