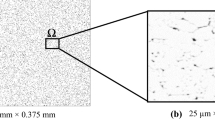
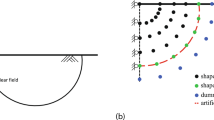
Abstract
Surrogate models for hotspot ignition and growth rates were presented in Part I (Nassar et al., Shock Waves 29(4):537–558, 2018), where the hotspots were formed by the collapse of single cylindrical voids. Such isolated cylindrical voids are idealizations of the void morphology in real meso-structures. This paper therefore investigates the effect of non-cylindrical void shapes and void–void interactions on hotspot ignition and growth. Surrogate models capturing these effects are constructed using a Bayesian Kriging approach. The training data for machine learning the surrogates are derived from reactive void collapse simulations spanning the parameter space of void aspect ratio, void orientation \( (\theta ) \), and void fraction \( (\phi ) \). The resulting surrogate models portray strong dependence of the ignition and growth rates on void aspect ratio and orientation, particularly when they are oriented at acute angles with respect to the imposed shock. The surrogate models for void interaction effects show significant changes in hotspot ignition and growth rates as the void fraction increases. The paper elucidates the physics of hotspot evolution in void fields due to the creation and interaction of multiple hotspots. The results from this work will be useful not only for constructing meso-informed macroscale models of HMX, but also for understanding the physics of void–void interactions and sensitivity due to void shape and orientation.


















Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Lee, E.L., Tarver, C.M.: Phenomenological model of shock initiation in heterogeneous explosives. Phys. Fluids 23(12), 2362–2372 (1980). https://doi.org/10.1063/1.862940
Sen, O., Rai, N., Diggs, A., Hardin, D., Udaykumar, H.: Multi-scale shock-to-detonation simulation of pressed energetic material: a meso-informed ignition and growth model. J. Appl. Phys. 124(8), 085110 (2018). https://doi.org/10.1063/1.5046185
Nassar, A., Rai, N.K., Sen, O., Udaykumar, H.: Modeling mesoscale energy localization in shocked HMX, part I: machine-learned surrogate models for the effects of loading and void sizes. J Shock Waves 29(4), 537–558 (2018). https://doi.org/10.1007/s00193-018-0874-5
Welle, E.J., Molek, C.D., Wixom, R.R., Samuels, P.: Microstructural effects on the ignition behavior of HMX. J. Phys. Conf. Ser. 500(5), 052049 (2014). https://doi.org/10.1088/1742-6596/500/5/052049
Molek, C., Welle, E.: Private communication. Image obtained by Ryan Wixom (LANL)
Levesque, G.A., Vitello, P.: The effect of pore morphology on hot spot temperature. Propellants Explos. Pyrotech. 40(2), 303–308 (2015). https://doi.org/10.1002/prep.201400184
Rai, N.K., Schmidt, M.J., Udaykumar, H.S.: Collapse of elongated voids in porous energetic materials: effects of void orientation and aspect ratio on initiation. Phys. Rev. Fluids 2(4), 043201 (2017). https://doi.org/10.1103/PhysRevFluids.2.043201
Kapahi, A., Udaykumar, H.: Dynamics of void collapse in shocked energetic materials: physics of void–void interactions. Shock Waves 23(6), 537–558 (2013). https://doi.org/10.1007/s00193-013-0439-6
Swantek, A., Austin, J.: Collapse of void arrays under stress wave loading. J. Fluid Mech. 649, 399–427 (2010). https://doi.org/10.1017/S0022112009993545
Bourne, N., Field, J.: Shock-induced collapse of single cavities in liquids. J. Fluid Mech. 244, 225–240 (1992). https://doi.org/10.1017/S0022112092003045
McDonald, S.A., Millett, J.C.F., Bourne, N.K., Bennett, K., Milne, A.M., Withers, P.J.: The shock response, simulation and microstructural determination of a model composite material. J. Mater. Sci. 42(23), 9671–9678 (2007). https://doi.org/10.1007/s10853-007-1961-7
Menikoff, R.: Pore collapse and hot spots in HMX. AIP Conf. Proc. 706, 393–396 (2004)
Tran, L., Udaykumar, H.S.: Simulation of void collapse in an energetic material, part I: inert case. J. Propuls. Power 22(5), 947–958 (2006). https://doi.org/10.2514/1.13146
Tran, L., Udaykumar, H.S.: Simulation of void collapse in an energetic material, part 2: reactive case. J. Propul. Power 22(5), 959–974 (2006). https://doi.org/10.2514/1.13147
Kapahi, A., Udaykumar, H.: Three-dimensional simulations of dynamics of void collapse in energetic materials. Shock Waves 25(2), 177–187 (2015). https://doi.org/10.1007/s00193-015-0548-5
Kapila, A.K., Schwendeman, D.W., Gambino, J.R., Henshaw, W.D.: A numerical study of the dynamics of detonation initiated by cavity collapse. Shock Waves 25(6), 1–28 (2015). https://doi.org/10.1007/s00193-015-0597-9
Springer, H.K., Tarver, C.M., Bastea, S.: Effects of high shock pressures and pore morphology. AIP Conf. Proc. 1793, 080002 (2015). https://doi.org/10.1063/1.4971608
Rai, N.K., Udaykumar, H.S.: Mesoscale simulation of reactive pressed energetic materials under shock loading. J. Appl. Phys. 118(24), 245905 (2015). https://doi.org/10.1063/1.4938581
Rai, N.K., Udaykumar, H.: Three-dimensional simulations of void collapse in energetic materials. Phys. Rev. Fluids 3(3), 033201 (2018). https://doi.org/10.1103/PhysRevFluids.3.033201
Nichols, A., Tarver, C.M.: A Statistical Hot Spot Reactive Flow Model for Shock Initiation and Detonation of Solid High Explosives. Lawrence Livermore National Lab, Livermore (2002)
Saurel, R., Fraysse, F., Furfaro, D., Lapebie, E.: Multiscale multiphase modeling of detonations in condensed energetic materials. Comput. Fluids 159, 95–111 (2017). https://doi.org/10.1016/j.compfluid.2017.09.006
Massoni, J., Saurel, R., Baudin, G., Demol, G.: A mechanistic model for shock initiation of solid explosives. Phys. Fluids (1994-present) 11(3), 710–736 (1999). https://doi.org/10.1063/1.869941
Sambasivan, S., Kapahi, A., Udaykumar, H.S.: Simulation of high speed impact, penetration and fragmentation problems on locally refined Cartesian grids. J. Comput. Phys. 235, 334–370 (2012). https://doi.org/10.1016/j.jcp.2012.10.031
Kapahi, A., Sambasivan, S., Udaykumar, H.: A three-dimensional sharp interface Cartesian grid method for solving high speed multi-material impact, penetration and fragmentation problems. J. Comput. Phys. 241, 308–332 (2013). https://doi.org/10.1016/j.jcp.2013.01.007
Rai, N.K., Schmidt, M.J., Udaykumar, H.S.: High-resolution simulations of cylindrical void collapse in energetic materials: effect of primary and secondary collapse on initiation thresholds. Phys. Rev. Fluids 2(4), 043202 (2017). https://doi.org/10.1103/PhysRevFluids.2.043202
Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes, II. J. Comput. Phys. 83(1), 32–78 (1989). https://doi.org/10.1016/0021-9991(89)90222-2
Osher, S., Sethian, J.A.: Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 79(1), 12–49 (1988). https://doi.org/10.1016/0021-9991(88)90002-2
Fedkiw, R.P., Aslam, T., Merriman, B., Osher, S.: A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152(2), 457–492 (1999). https://doi.org/10.1006/jcph.1999.6236
Vanpoperynghe, J., Sorel, J., Aveille, J., Adenis, J.C.: Shock initiation of TATB and HMX explosive compositions. In: Proceedings, Eighth Symposium (International) on Detonation (Albuquerque, New Mexico, 1985). NSWC MP 86-194, p. 892. Naval Surface Weapons Center (1985)
Sen, O., Davis, S., Jacobs, G., Udaykumar, H.S.: Evaluation of convergence behavior of metamodeling techniques for bridging scales in multi-scale multimaterial simulation. J. Comput. Phys. 294, 585–604 (2015). https://doi.org/10.1016/j.jcp.2015.03.043
Sen, O., Gaul, N.J., Choi, K.K., Jacobs, G., Udaykumar, H.S.: Evaluation of kriging based surrogate models constructed from mesoscale computations of shock interaction with particles. J. Comput. Phys. 336, 235–260 (2017). https://doi.org/10.1016/j.jcp.2017.01.046
Gaul, N.J., Cowles, M.K., Cho, H., Choi, K., Lamb, D.: Modified Bayesian Kriging for noisy response problems for reliability analysis. American Society of Mechanical Engineers V02BT03A060-V002BT003A060 (2015). https://doi.org/10.1115/DETC2015-47370
Lu, C., Grieb, N., Sambasivan, S., Udaykumar, H.: Multiresolution augmented artificial neural networks for modeling of particle laden compressible flows: integrated and multidisciplinary modeling and simulation. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, AIAA Paper 2010-811 (2012). https://doi.org/10.2514/6.2010-811
Ma, X., Zabaras, N.: An adaptive hierarchical sparse grid collocation algorithm for the solution of stochastic differential equations. J. Comput. Phys. 228(8), 3084–3113 (2009). https://doi.org/10.1016/j.jcp.2009.01.006
Walker, F., Wasley, R.: A general model for the shock initiation of explosives. Propellants Explos. Pyrotech. 1(4), 73–80 (1976). https://doi.org/10.1002/prep.19760010403
Nassar, A., Rai, N.K., Udaykumar, H.S.: Criticality conditions of heterogeneous energetic materials under shock loading. APS Shock Compression of Condensed Matter Meeting Abstracts (2017)
Lee, S., Sen, O., Rai, N.K., Gaul, N.J., Choi, K.K., Udaykumar, H.S.: Effects of parametric uncertainty on multi-scale model predictions of shock response of a pressed energetic material. J. Appl. Phys. 125(23), 235104 (2019). https://doi.org/10.1063/1.5098955
MATLAB: The MathWorks, Inc., Natick, MA, USA (2015)
Jackson, T.L., Jost, A.M., Zhang, J., Sridharan, P., Amadio, G.: Multi-dimensional mesoscale simulations of detonation initiation in energetic materials with density-based kinetics. Combust. Theor. Model. 22(2), 1–25 (2017). https://doi.org/10.1080/13647830.2017.1401121
Zhang, J., Jackson, T.L.: Effect of microstructure on the detonation initiation in energetic materials. Shock Waves 29(2), 327–338 (2019). https://doi.org/10.1007/s00193-017-0796-7
Ponthot, J.-P.: Unified stress update algorithms for the numerical simulation of large deformation elasto-plastic and elasto-viscoplastic processes. Int. J. Plast. 18(1), 91–126 (2002). https://doi.org/10.1016/S0749-6419(00)00097-8
Menikoff, R., Sewell, T.D.: Constituent properties of HMX needed for mesoscale simulations. Combust. Theor. Model. 6(1), 103–125 (2002). https://doi.org/10.1088/1364-7830/6/1/306
Strang, G.: On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5(3), 506–517 (1968). https://doi.org/10.1137/0705041
Fehlberg, E.: Classical Fifth-, Sixth-, Seventh-, and Eighth-Order Runge-Kutta Formulas with Stepsize Control. National Aeronautics and Space Administration, Washington (1968)
Sewell, T.D., Menikoff, R.: Complete equation of state for β-HMX and implications for initiation. AIP Conf. Proc. 706, 157 (2003). https://doi.org/10.1063/1.1780207
Tarver, C.M., Chidester, S.K., Nichols, A.L.: Critical conditions for impact-and shock-induced hot spots in solid explosives. J. Phys. Chem. 100(14), 5794–5799 (1996). https://doi.org/10.1021/jp953123s
Acknowledgements
The authors gratefully acknowledge the financial support from the Air Force Research Laboratory Munitions Directorate, Eglin AFB, under Contract Number FA8651-16-1-0005. The authors are also thankful to K.K. Choi at the University of Iowa and Nicholas J. Gaul at RAMDO LLC, Iowa City, for providing the computational code for the Modified Bayesian Kriging Method.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by E. Timofeev.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Governing equations
The hyperbolic conservation laws for mass, momentum, and energy are solved:
and
The source term \( {\dot{\mathcal{E}}} \) in (30) is the rise in specific internal energy of the system due to heat released in the decomposition of solid HMX into gaseous reaction products, and \( \sigma_{ij} \) is the Cauchy stress tensor and is decomposed into volumetric and deviatoric component, i.e.,
The deviatoric stress tensor, \( S_{ij} \), is evolved using the following evolution equation.
where \( D_{ij} \) is the strain rate tensor \( \Omega_{ij}\) is the spin tensor, and G is the shear modulus of material. First, the deviatoric stresses are evolved using an elastic response and then mapped back to the yield surface using a radial return algorithm [41]. The yield surface is given by the function \( f = S_{\text{e}} - \sigma_{y} \), where \( S_{\text{e}} = \sqrt {\frac{3}{2}\left( {S_{ij} S_{ij} } \right)} \). The yield strength, \( \sigma_{y} \), is taken to be a constant and set to \( 260\;{\text{MPa}} \) [42] for HMX, i.e., hardening, and visco-plastic effects are neglected in the mesoscale computational models. A detailed description of the governing equations and radial return algorithm is provided in previous work [18, 19, 23,24,25].
The chemical species are evolved in time by solving the conservation equation:
where \( Y_{i} \) is the mass fraction of the \( i{\text{th}} \) species and \( \dot{Y}_{i} \) is the production rate source term for the \( i{\text{th}} \) species. The numerical stiffness in solving the reactive set of equations is circumvented by using a Strang operator splitting approach [43], where first the advection of species is performed using the flow time step to obtain predicted species values:
In the second step, the evolution of the species mass fraction due to chemical reactions is calculated:
The species evolution (35) is advanced in time using a fifth-order Runge–Kutta–Fehlberg method [44], which uses an internal adaptive time-stepping scheme to deal with the stiffness of the chemical kinetic equations.
Appendix 2: Constitutive and reaction models
The pressure in the mesoscale in (31) is obtained from a Birch–Murnaghan equation of state [45], which can be written in the general Mie–Gruneisen form as:
where
Void collapse under shock loading can lead to the melting of HMX; therefore, thermal softening of HMX is modeled using the Kraut–Kennedy relation, \( T_{\text{m}} = T_{{{\text{m}}0}} \left( {1 + a\frac{\Delta V}{{V_{0} }}} \right) \), with model parameters provided in the work of Menikoff et al. [42]. Once the temperature exceeds the melting point of HMX, the deviatoric strength terms are set to zero. Furthermore, the specific heat of HMX is known to change significantly with temperature. The variation of specific heat is modeled as a function of temperature as suggested in [42].
The chemical decomposition of HMX is modeled using a three-step mechanism proposed by Tarver et al. [46]. A detailed description of the implementation of the three-step model in the current numerical framework is presented in a previous work [7]. Here, a brief overview of the reaction model and its implementation is provided.
Chemical decomposition of HMX takes place in three steps involving four different species:
and
The solid HMX (species 1, mass fraction \( Y_{1} \)) under high temperature decomposes into fragments (species 2, \( Y_{2} \)). The fragments are further decomposed to intermediate gases (species 3, \( Y_{3} \)) which are later converted to the final gases (species 4, \( Y_{4} \)) through exothermic reactions leading to high temperatures in the hotspot. In the absence of information about the equations of state for the intermediate and the final products, in this work, it is assumed that these intermediates and the products follow the same cold curves as the bulk material.
The change in temperature because of the chemical decomposition of HMX is calculated by solving the evolution equation:
where \( \rho \) is the density of HMX, \( C_{p} \) is the specific heat of HMX, \( T \) is the temperature, \( k \) is the thermal conductivity of HMX, and \( \dot{Q}_{\text{R}} \) is the total heat release rate because of the chemical reaction. The values of \( C_{p} \), λ, and \( \dot{Q}_{\text{R}} \) are obtained from the work of Tarver et al. [46]. The source term in (30) is computed by setting \( {\dot{\mathcal{E}}} = C_{v} \dot{T} \), where \( C_{v} \) is the specific heat of HMX at constant volume.
Rights and permissions
About this article
Cite this article
Roy, S., Rai, N.K., Sen, O. et al. Modeling mesoscale energy localization in shocked HMX, Part II: training machine-learned surrogate models for void shape and void–void interaction effects. Shock Waves 30, 349–371 (2020). https://doi.org/10.1007/s00193-019-00931-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-019-00931-1