Skip to main content
SpringerLink
Log in

Computational study of shock wave control by pulse energy deposition

  • Original Article
  • Published:
Shock Waves Aims and scope Submit manuscript

Abstract

We have developed a computational code based on the axisymmetric Navier–Stokes equations with thermochemical kinetics for assessing wave drag reduction and other effects in pulse-energy deposition ahead of a bow shock by means of full simulations from generation of a laser-induced blast wave to interaction with the bow shock. Thermochemical nonequilibrium computations can reproduce the process of blast wave formation with laser ray tracing, and the computed low-density core inside the blast wave has a teardrop-like shape, depending on the laser input condition. The flowfield interacting with a bow shock formed in Mach 5 flow was computed. The result suggests that the shape of the low-density core affects the resultant wave drag, and parameters of an incident laser beam should be taken into account in exploring the optimal condition of the proposed wave-drag scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Bogdonoff, S.M., Vas, I.E.: Preliminary investigations of spiked bodies at hypersonic speeds. J. Aerosp. Sci. 26, 65–74 (1959)

    MATH  Google Scholar 

  2. Crawford, D.H.: Investigations of the flow over a spiked-nose hemisphere-cylinder at a Mach number of 6.8. NASA TN D-118, Langley Research Center (1959)

  3. Maull, D.J.: Hypersonic flow over axially symmetric spiked bodies. J. Fluid Mech. 8, 584–592 (1960)

    Article  MathSciNet  Google Scholar 

  4. Georgievsky, P.Y., Levin, V.A.: Supersonic flow over bodies in the presence of external energy input. Pis’ma v Zhurnal Tekhnicheskoi Fiziki 14, 684–687 (1988)

    Google Scholar 

  5. Bushnell, D.M.: Supersonic aircraft drag reduction. AIAA Paper 90–1596 (1990)

  6. Myrabo, L.N., Raizer, Y.P.: Laser-induced air spike for advanced transatmospheric vehicle. AIAA Paper 94–2451 (1994)

  7. Riggins, D.W., Nelson, H.F., Johnson, E.: Blunt-body wave drag reduction using focused energy deposition. AIAA J. 37, 460–467 (1999)

    Article  Google Scholar 

  8. Takaki, R.: Numerical simulation of heating rate reduction by directed energy. J. Jpn. Soc. Aeronaut. Space Sci. 50, 37–42 (2002)

    Google Scholar 

  9. Georgievsky, P.Y., Levin, V.A.: Unsteady interaction of a sphere with atmospheric temperature inhomogeneity at supersonic speed. Fluid Dyn. 28, 568–574 (1993)

    Article  Google Scholar 

  10. Tretyakov, P.K., Garanin, G.N., Grachev, V.L., Ponomarenko, A.G., Tishchenko, V.N., Yakovlev, V.I.: The supersonic flow control over the bodies with the use of power optical pulsating discharge. Doklady Akademii Nauk 351, 339–340 (1996)

    Google Scholar 

  11. Adelgren, R.G., Elliott, G.S., Knight, D.D., Zheltovodov, A.A., Beutner, T.J.: Energy deposition in supersonic flows. AIAA Paper 2001–0885 (2001)

  12. Kandala, R., Candler, G.V.: Numerical studies of laser-induced energy deposition for supersonic flow control. AIAA J. 42, 2266–2275 (2004)

    Article  Google Scholar 

  13. Georgievsky, P.Y., Levin, V.A.: Bow shock waves structures control by pulse-periodic energy input. AIAA Paper 2004–1019 (2004)

  14. Adelgren, R.G., Yan, H., Elliott, G.S., Knight, D.D., Beutner, T.J., Zheltovodov, A.A.: Control of Edney IV interaction by pulsed laser energy deposition. AIAA J. 43, 256–269 (2005)

    Article  Google Scholar 

  15. Zheltovodov, A.A., Pimonov, E.A., Knight, D.D.: Energy deposition influence on supersonic flow over axisymmetric bodies. AIAA Paper 2007–1230 (2007)

  16. Knight, D., Kolesnichenko, Y.F., Brovkin, V., Khmara, D., Lashkov, V., Mashek, I.: Interaction of microwave-generated plasma with a blunt body at Mach 2.1. AIAA Paper 2009–0846 (2009)

  17. Sedov, L.I.: Similarity and dimensional methods in mechanics 10th edn, translated by Volkovets A.G., CRC Press, Boca Raton (1993)

  18. Taguchi, S., Ohnishi, N., Furudate, M., Sawada, K.: Numerical analysis of drag reduction for supersonic blunt body by pulse energy deposition. AIAA Paper 2007–1235 (2007)

  19. Ogino, Y., Ohnishi, N., Taguchi, S., Sawada, K.: Baroclinic vortex influence on wave drag reduction induced by pulse energy deposition. Phys. Fluids 21, 066102 (2009)

    Article  Google Scholar 

  20. Schülein, E., Zheltovodov, A.A., Pimonov, E.A., Loginov, M.S.: Study of the bow shock interaction with laser-pulse-heated air bubbles. AIAA Paper 2009–3568 (2009)

  21. Park, C.: Nonequilibrium Hypersonic Aerothermodynamics. Wiley and Sons, New York (1989)

    Google Scholar 

  22. Edwards, A.L., Fleck Jr, J.A.: Two-dimensional modeling of aerosol-induced breakdown in air. J. Appl. Phys. 50, 4307–4313 (1979)

    Article  Google Scholar 

  23. Blottner, F.G., Johnson, M., Ellis, M.: Chemically reacting viscous flow program for multi-component gas mixture. Report SC-RR-70-754, Sandia National Laboratories (1971)

  24. Vincenti, W.G., Kruger, C.H.: Introduction to Physical Gas Dynamics. Wiley and Sons, New York (1965)

  25. Wilke, C.R.: A viscosity equation for gas mixtures. J. Chem. Phys. 18, 517–519 (1950)

    Article  Google Scholar 

  26. Park, C.: Review of chemical-kinetic problems of future NASA Missions, Part 1: earth entries. J. Thermophys. Heat Transf. 7, 385–398 (1993)

    Article  Google Scholar 

  27. Park, C.: Assessment of two-temperature kinetic model for ionizing air. J. Thermophys. Heat Transf. 3, 233–244 (1989)

    Article  Google Scholar 

  28. Ohnishi, N., Ogino, Y., Sawada, K., Ohtani, T., Sasoh, A.: Numerical analysis of laser-driven in-tube accelerator operation. AIAA Paper 2005–749 (2005)

  29. Wada Y., Liu, M.S.: A flux splitting scheme with high-resolution and robustness for discontinuities. AIAA Paper 94–0083 (1994)

  30. Van Leer, B.: Towards the ultimate conservation difference scheme V, a second-order sequel to Godunov’s method. J. Comput. Phys. 32, 101–136 (1979)

    Article  Google Scholar 

  31. Eberhardt, S., Imlay, S.: Diagonal implicit scheme for computing flows with finite rate chemistry. J. Thermophys. Heat Transf. 5, 257–265 (1991)

    Article  Google Scholar 

  32. Mori, K., Komurasaki, K., Arakawa, Y.: Influence of the focusing f number on the heating regime transition in laser absorption waves. J. Appl. Phys. 92, 5663–5667 (2002)

    Article  Google Scholar 

  33. Knight, D.: Survey of aerodynamic drag reduction at high speed by energy deposition. J. Propuls. Power 24, 1153–1167 (2008)

    Article  Google Scholar 

  34. Kremeyer, K., Sebastian, K., Shu, C.-W.: Computational study of shock mitigation and drag reduction by pulsed energy lines. AIAA J. 44, 1720–1731 (2006)

    Article  Google Scholar 

  35. Sakai, T., Sekiya, Y., Mori, K., Sasoh, A.: Interaction between laser-induced plasma and shock wave over a blunt body in a supersonic flow. J. Aerosp. Eng. 222, 605–617 (2008)

    Google Scholar 

Download references

Acknowledgments

This study was supported by the Program for Improvement of Research Environment for Young Researchers from Special Coordination Funds for Promoting Science and Technology (SCF) commissioned by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan and a Grant-in-Aid from the Japan Society for the Promotion of Science (JSPS) Fellows. The authors appreciate the anonymous reviewers who provided valuable comments for revision.

Author information

Author notes

  1. M. Tate

    Present address: JFE Steel Corporation, 1-1 Ohgishima, Kawasaki-ku, Kawasaki, 210-0868, Japan

Authors and Affiliations

  1. Department of Aerospace Engineering, Tohoku University, 6-6-01 Aramaki-Aza-Aoba, Aoba-ku, Sendai, 980-8579, Japan

    N. Ohnishi, M. Tate & Y. Ogino

Authors
  1. N. Ohnishi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Tate
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y. Ogino
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. Ohnishi.

Additional information

Communicated by E. Timofeev.

Appendices

Appendix: A validation of laser-induced blast wave

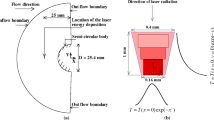
Laser-induced blast waves have been studied in many experiments in terms of shock wave propagation and plasma-surface evolution. Mori et al. [32] measured the positions of the shock wave front and the plasma front in their laser blast experiment using a CO\(_2\) laser. The experiment setup was similar to our computational conditions in this paper, so our simulation of laser-induced blast waves in air can be validated by comparison with their measurements.

Axisymmetric simulation conditions were set by following their experiment. The input laser profile consists of a 120-ns pulse part and an exponential decay part like Fig. 2. Input energy is 10 J with maximum power of 24 WM and is numerically divided into 160 rays. The incident laser is focused with 10.6 \(\upmu \)m wavelength and \(f\)-number of 2.2. The computational domain covers a 32-mm\(\times \)12-mm rectangular area with 161\(\times \)61 grids.

Figure 8 depicts the time evolution of the shock front and the plasma front toward the incident laser at the axis of symmetry, compared with experiment data [32]. The focal position is adjusted for a later shock position, since the precise focal point is difficult to obtain in the experiment. In the simulation, the shock was detected by density jump, and the plasma front was detected by vibrational temperature jump. Agreement of shock speed and plasma evolution with the experiment, especially in the later time, suggests that laser-energy deposition is predicted well by the developed code.

In the very early time, plasma development is slightly faster than the experiment. This may be due to the fact that the initial breakdown process cannot be described by the present code. However, detailed prediction in the early time is not necessary in the context of the interaction with a bow shock wave, because the blast wave develops sufficiently in the time of interest and approaches the measured trajectory at a later time.

Appendix: B Grid dependency of the interaction between bow shock and blast wave

In order to check the grid dependency of the flowfield induced by interaction between the bow shock and the blast wave, three different grids were prepared to represent the computational domain used in Sect. 4. The number of original grids is 181\(\times \)151, and those of the two denser grids are 261\(\times \)226 and 341\(\times \)301.

Fig. 8
figure 8

Time evolution of the shock front and the plasma front in the laser-induced blast wave obtained by our code (lines) and past experiment [32] (symbols)

Full size image

Computed drag and reduction energy were compared among simulations with the three grids. In Fig. 9a, the time variation of drag is almost the same among them, while some differences appear in small oscillations of drag. The minute structure induced by the interaction in the shock layer depends on grid density and may produce such differences. However, large oscillations and their amplitudes agree among the different grids.

Fig. 9
figure 9

Time histories of drag and reduction energy with three different grids. a Drag. b Reduction energy

Full size image

Small oscillations in drag history are not important in drag-reduction analysis. Actually, reduction energy results in similar values within 5% difference (Fig. 9b). Since the main objective is to present the effects of realistic plasma deposition and heating environment in the drag reduction scheme of pulse energy deposition, an accurate prediction with reduced numerical error less than the above level is beyond the scope of the present paper.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ohnishi, N., Tate, M. & Ogino, Y. Computational study of shock wave control by pulse energy deposition. Shock Waves 22, 521–531 (2012). https://doi.org/10.1007/s00193-012-0407-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00193-012-0407-6

Keywords

Search

Navigation