Evaluation of gravitational curvatures for a tesseroid and spherical shell with arbitrary-order polynomial density

Abstract

In recent years, there are research trends from constant to variable density and low-order to high-order gravitational potential gradients in gravity field modeling. Under the research circumstances, this paper focuses on the variable density model for gravitational curvatures (or gravity curvatures, third-order derivatives of gravitational potential) of a tesseroid and spherical shell in the spatial domain of gravity field modeling. In this contribution, the general formula of the gravitational curvatures of a tesseroid with arbitrary-order polynomial density is derived. The general expressions for gravitational effects up to the gravitational curvatures of a spherical shell with arbitrary-order polynomial density are derived when the computation point is located above, inside, and below the spherical shell. When the computation point is located above the spherical shell, the general expressions for the mass of a spherical shell and the relation between the radial gravitational effects up to arbitrary-order and the mass of a spherical shell with arbitrary-order polynomial density are derived. The influence of the computation point’s height and latitude on gravitational curvatures with the polynomial density up to fourth-order is numerically investigated using tesseroids to discretize a spherical shell. Numerical results reveal that the near-zone problem exists for the fourth-order polynomial density of the gravitational curvatures, i.e., relative errors in $\log _{10}$ scale of gravitational curvatures are large than 0 below the height of about 50 km by a grid size of $15'\times 15'$. The polar-singularity problem does not occur for the gravitational curvatures with polynomial density up to fourth-order because of the Cartesian integral kernels of the tesseroid. The density variation can be revealed in the absolute errors as the superposition effects of Laplace parameters of gravitational curvatures other than the relative errors. The derived expressions are examples of the high-order gravitational potential gradients of the mass body with variable density in the spatial domain, which will provide the theoretical basis for future applications of gravity field modeling in geodesy and geophysics.

1 Introduction

Generally, different structures of the Earth (e.g., atmosphere, ice, water, topography, sediment, crust, mantle, and core) have different densities. For example, the density from the surface to the inner core of the Earth varied from 1020.0 to 13088.5 $\mathrm {kg\ m^{-3}}$ in the preliminary reference Earth model (Dziewonski and Anderson 1981) and from 2651.0 to 13012.2 $\mathrm {kg\ m^{-3}}$ in the radial ek137 model (Kennett 2020). The density hypothesis and digital models (e.g., CRUST1.0 (Laske et al. 2013) and UNB_TopoDens (Sheng et al. 2019)) have wide applications in geodesy and geophysics, e.g., variable topographic density on the determination of gravimetric geoid (Huang et al. 2001; Tziavos and Featherstone 2001; Kuhn 2003; Sjöberg 2004; Kiamehr 2006; Abbak 2020), geoid-to-quasigeoid separation (Tenzer et al. 2016, 2021), and gravity forward modeling of topographic and crustal effects (Eshagh 2009c; Novák et al. 2013; Tenzer et al. 2015; Yang et al. 2018; Rathnayake et al. 2020).

Among the commonly used density models, the polynomial density was extensively applied in the spatial domain of gravity field modeling. Regarding a right rectangular prism, its gravitational effects (e.g., gravitational potential (GP), gravity vector (GV) or gravitational attraction, and gravity gradient tensor (GGT)) were derived in different types of the polynomial density, i.e., the GV with the depth-dependent cubic polynomial density (García-Abdeslem 2005) and an arbitrary-order polynomial density (Zhang and Jiang 2017), GV and GGT in the Fourier domain with the depth-dependent polynomial density (Wu and Chen 2016; Wu 2018), GGT with the depth-dependent density (Jiang et al. 2018), and GP, GV, and GGT with the depth-dependent nth-order polynomial density (Karcol 2018; Fukushima 2018b). Similarly, the gravitational effects of a spherical shell were derived in the form of the polynomial density, i.e., the GP and GV with the radial fifth-order polynomial density (Karcol 2011) and the GP, GV, and GGT with the linear, quadratic, and cubic order polynomial density (Lin et al. 2020). Regarding a tesseroid (Anderson 1976; Heck and Seitz 2007), its gravitational effects up to the GGT were derived in the form of the linear density in Fukushima (2018a), Lin and Denker (2019), and Soler et al. (2019). Lin et al. (2020) presented the general expressions for the GP, GV, and GGT of a tesseroid in the form of the polynomial density.

With the first measurement of radial gravitational curvatures (or gravity curvatures, GC, third-order derivatives of the gravitational potential) using the atom interferometry sensors in the laboratory condition (Rosi et al. 2015), the subsequent study of the GC was focused on their theory and simulation applications in geodesy and geophysics (Šprlák and Novák 2015, 2016, 2017; Šprlák et al. 2016; Hamáčková et al. 2016; Sharifi et al. 2017; Novák et al. 2017; Pitoňák et al. 2017, 2018, 2020; Deng and Shen 2018a, b, 2019; Novák et al. 2019; Du and Qiu 2019; Romeshkani et al. 2020, 2021). The GC were more sensitive to field sources than the low-order gravitational effects (i.e., GP, GV, and GGT) (Heck 1984; Du and Qiu 2019). Numerical results showed that they were more sensitive to local characteristics of the gravity field (Romeshkani et al. 2020), can better describe areas with large terrain undulations and the junction of the land and sea (Deng and Shen 2019), and can more accurately identify the near-underground shallow density structure in the spatial domain (e.g., caves, salt domes, sediment base morphology, continental margins, and hidden fault systems) (Novák et al. 2019) than the low-order gravitational effects. These advantages of the GC are important for studying the distribution of materials and geological structures within the Earth.

Currently, the expressions for the GC of a tesseroid and a spherical shell with the constant density were derived in Deng and Shen (2018a). Meanwhile, Deng (2022) recently derived the analytical solutions for the gravitational curvatures of a spherical cap and spherical zonal band with the constant density. With the increased depth inside the Earth, the actual density shows a complex rule of variable density. The constant density is not enough to represent the actual density variation of the earth for the GC. In other words, the existing constant density assumption cannot meet the demand for a real complex environment with the variable density. Thus, it is essential to investigate their variable density forms, especially the polynomial density. This study focuses on the derivation of arbitrary-order (i.e., $N \ge 0$) polynomial density for the GC of a tesseroid and spherical shell.

This study goes beyond the previous studies in that the general formulae of the GC of a tesseroid with Nth-order polynomial density and the general analytical expressions for the GC of a spherical shell with Nth-order polynomial density are derived. In addition, we derive the general analytical expressions for gravitational effects (e.g., GP, GV, and GGT) of a spherical shell with Nth-order polynomial density when the computation point is located above, inside, and below the spherical shell. The derived polynomial density expressions of the GC would more accurately describe the complex density characteristics of the Earth’s interior than the constant density expressions, which will lay a theoretical foundation for the applications of gravity field modeling in geodesy and geophysics.

This paper is organized as follows. Section 2 presents the theoretical aspects, in which Sect. 2.1 provides the general formula of the GC of a tesseroid with Nth-order polynomial density. In Sect. 2.2, the analytical expressions for gravitational effects up to the GC of a spherical shell with Nth-order polynomial density are derived when the computation point is located above, inside, and below the spherical shell. Section 3 performs the numerical experiments, where the setup of the numerical experiments is provided in Sect. 3.1 and the effects of density values on the gravitational effects of a spherical shell are studied in Sect. 3.2. The influences of the computation point’s height and latitude on the GC with the polynomial density up to fourth-order are investigated in Sects. 3.3 and 3.4, respectively. Finally, the conclusions of this paper and outlooks on future research work are summarized in Sect. 4.

2 Theoretical aspects

In this section, the theoretical contents are presented in detail. Based on the previous works of Deng and Shen (2018b, 2019) and Lin et al. (2020), the formula of the GC of a tesseroid with arbitrary-order polynomial density is derived in Sect. 2.1. Section 2.2 derives the expressions for the GC of a spherical shell with arbitrary-order polynomial density based on the work of Lin et al. (2020). The general formula of the mass for a spherical shell with arbitrary-order polynomial density is derived in Sect. 2.2. Moreover, Sect. 2.2 derives the general relation between the radial gravitational effects up to arbitrary-order and the mass of a spherical shell with arbitrary-order polynomial density when the computation point P is outside the spherical shell.

2.1 The GC of a tesseroid with arbitrary-order polynomial density

Regarding the variable density model for a tesseroid (see Fig. 1), Lin et al. (2020) derived the GP, GV, and GGT of a tesseroid with a polynomial density model up to Nth-order in the vertical direction and evaluated these gravitational effects with a polynomial density model up to cubic order (i.e., $N=3$) in the numerical experiments. Due to the potential benefits of the GC in geodesy and geophysics revealed in the introduction, it is essential to investigate the variable polynomial density model for the GC of a tesseroid. In this section, based on the previous works of Deng and Shen (2018b, 2019) and Lin et al. (2020), the general expression for the GC of a tesseroid with Nth-order polynomial density is derived, and the detailed components of the GC are provided as well.

Fig. 1

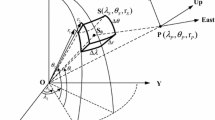
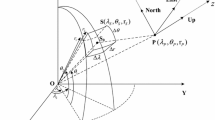
The geometry of a tesseroid in the spherical coordinate system revised from Fig. 4 of Heck and Seitz (2007). P and Q are the computation (or field, observation) and running integration points with their longitudes ($\lambda$ and $\lambda '$), latitudes ($\varphi$ and $\varphi '$), and geocentric distances (r and $r'$), respectively. $\varDelta \lambda =\lambda _2-\lambda _1$, $\varDelta \varphi =\varphi _2-\varphi _1$, and $\varDelta r = r_2-r_1$ are the longitude, latitude, and radial dimensions of a tesseroid, respectively. P(x, y, z) is in the local north-oriented frame system with x, y, and z pointing to the north, east, and radial up directions, respectively

Replacing the constant density $\rho$ in Eq. (3) of Deng and Shen (2018b) by the variable density model $\rho (r')$, the optimized formula of the GC ($V_{\alpha \beta \gamma }$ with $\alpha ,\beta ,\gamma$ = x, y, z) of a tesseroid in Cartesian integral kernels with the variable density model can be derived as:

$$\begin{aligned}{} & {} V_{\alpha \beta \gamma } (\lambda ,\varphi ,r) = G \int _{\lambda _1}^{\lambda _2} \int _{\varphi _1}^{\varphi _2} \int _{r_1}^{r_2} \rho (r') r'^{2} \cos \varphi ' I_{\alpha \beta \gamma } (\lambda ', \varphi ',r') \textrm{d} r' \textrm{d} \varphi ' \textrm{d} \lambda ' \end{aligned}$$

(1)

$$\begin{aligned} I_{\alpha \beta \gamma }(\lambda ', \varphi ',r')= 3 \left( \frac{5 \varDelta _{\alpha } \varDelta _{\beta } \varDelta _{\gamma }}{\ell ^{7}}-\frac{p_{\alpha \beta \gamma }}{\ell ^{5}} \right) \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \ell =\sqrt{r'^2+r^2-2r'r \left( \sin \varphi \sin \varphi '+\cos \varphi \cos \varphi ' \cos (\lambda '-\lambda )\right) } \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \varDelta _x=r'\left( \cos \varphi \sin \varphi '-\sin \varphi \cos \varphi ' \cos (\lambda '-\lambda ) \right) \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \varDelta _y=r' \cos \varphi '\sin (\lambda '-\lambda ) \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \varDelta _z=r' \left( \sin \varphi \sin \varphi '+\cos \varphi \cos \varphi ' \cos (\lambda '-\lambda )\right) -r \end{aligned}$$

(6)

$$ \begin{aligned}{} & {} p_{\alpha \beta \gamma }=\left\{ \begin{array}{c c} 3 \varDelta _{\alpha } \ \ \ {} &{} \alpha =\beta =\gamma \\ 0\ \ \ {} &{} \alpha \ne \beta \ \& \ \alpha \ne \gamma \ \& \ \beta \ne \gamma \\ \varDelta _{\alpha } \ \ \ &{}\alpha \ne \beta \ \& \ \alpha \ne \gamma \ \& \ \beta =\gamma \\ \varDelta _{\beta } \ \ \ &{}\alpha \ne \beta \ \& \ \alpha =\gamma \ \& \ \beta \ne \gamma \\ \varDelta _{\gamma } \ \ \ &{} \alpha =\beta \ \& \ \alpha \ne \gamma \ \& \ \beta \ne \gamma \end{array}\right. \end{aligned}$$

(7)

where G is the Newtonian gravitational constant (i.e., $G=6.67430 \times 10^{-11}\ \mathrm {m^{3}\ kg^{-1}\ s^{-2}}$ (Tiesinga et al. 2021)). $[\lambda _1,\lambda _2]$, $[\varphi _1,\varphi _2]$, and $[r_1,r_2]$ are the longitude, latitude, and radial boundaries of a tesseroid. $I_{\alpha \beta \gamma }(\lambda ', \varphi ',r')$ is the Cartesian integral kernel of the GC of the tesseroid, which can be referred to in Eqs. (A.11–A.20) of Deng and Shen (2019). $\ell$, $\varDelta _x$, $\varDelta _y$, and $\varDelta _z$ in Eqs. (3–6) are from Eqs. (4) and (15) of Grombein et al. (2013). $(\lambda ,\varphi ,r)$ and $(\lambda ',\varphi ',r')$ are the spherical longitudes, latitudes, and geocentric distances of the computation point P and integration point Q, respectively. The computation point P is in the local north-oriented frame system with its coordinate origin at the computation point and x, y, and z pointing to the north, east, and radial up directions, respectively.

The formula of the polynomial density $\rho (r')$ of a tesseroid is presented as:

$$\begin{aligned} \rho (r')= & {} \rho _0 + \rho _1 r' + \rho _2 r'^{2} + \rho _3 r'^{3} +\cdots + \rho _N r'^{N}\nonumber \\= & {} \sum _{n=0}^{N} \rho _n r'^{n} \end{aligned}$$

(8)

where n and N are the integers and $n=0,1,2,3,...,N$ with $N \ge 0$. $\rho _n$ is the polynomial density coefficient with the unit $\mathrm {kg\ m^{-(n+3)}}$. For example, when $n=0$, $\rho _0$ is the constant density with the unit $\textrm{kg}\ \textrm{m}^{-3}$. Another method to obtain the expressions for the $\rho _n$ can be referred in Table 1 of Lin et al. (2020).

Substituting Eq. (8) into (1), the optimized formula of the GC ($V_{\alpha \beta \gamma }$) of a tesseroid in Cartesian integral kernels with Nth-order polynomial density is presented as:

$$\begin{aligned} V_{\alpha \beta \gamma } (\lambda ,\varphi ,r){} & {} = G \sum _{n=0}^{N} \rho _n \int _{\lambda _1}^{\lambda _2} \int _{\varphi _1}^{\varphi _2} \int _{r_1}^{r_2} \kappa _n I_{\alpha \beta \gamma }(\lambda ', \varphi ',r') \textrm{d} r' \textrm{d} \varphi ' \textrm{d} \lambda ' \end{aligned}$$

(9)

$$\begin{aligned} \kappa _n{} & {} =r'^{n+2} \cos \varphi ' \end{aligned}$$

(10)

Including the low-order gravitational potential gradients (i.e., V, $V_{\alpha }$, and $V_{\alpha \beta }$ with $\alpha ,\beta$ = x, y, z) presented in Eq. (3) of Lin et al. (2020), the general expressions for the gravitational effects up to the GC of a tesseroid in Cartesian integral kernels with Nth-order polynomial density are presented as:

$$\begin{aligned}{} & {} \begin{Bmatrix} V(\lambda , \varphi , r) \\ V_{\alpha }(\lambda , \varphi , r) \\ V_{\alpha \beta }(\lambda , \varphi , r) \\ V_{\alpha \beta \gamma }(\lambda , \varphi , r) \end{Bmatrix} = G \sum _{n=0}^{N} \rho _n \int _{r_1}^{r_2} \int _{\varphi _1}^{\varphi _2} \int _{\lambda _1}^{\lambda _2} \kappa _n \nonumber \\{} & {} \begin{Bmatrix} I(\lambda ', \varphi ',r') \\ I_{\alpha }(\lambda ', \varphi ',r') \\ I_{\alpha \beta }(\lambda ', \varphi ',r') \\ I_{\alpha \beta \gamma }(\lambda ', \varphi ',r') \end{Bmatrix} \textrm{d}\lambda ' \textrm{d} \varphi ' \textrm{d}r' = \sum _{n=0}^{N} \begin{Bmatrix} (V^{\textrm{tess}})_n \\ (V_{\alpha }^{\textrm{tess}})_n \\ (V_{\alpha \beta }^{\textrm{tess}})_n \\ (V_{\alpha \beta \gamma }^{\textrm{tess}})_n \end{Bmatrix} \end{aligned}$$

(11)

where $I(\lambda ', \varphi ',r')$, $I_{\alpha }(\lambda ', \varphi ',r')$, and $I_{\alpha \beta }(\lambda ', \varphi ',r')$ are the Cartesian integral kernels of the GP, GV, and GGT of a tesseroid, which can be referred to in Eq. (21) of Grombein et al. (2013) and Eqs. (A.1–A.10) of Deng and Shen (2019). The $(V^{\textrm{tess}})_n$, $(V_{\alpha }^{\textrm{tess}})_n$, $(V_{\alpha \beta }^{\textrm{tess}})_n$, and $(V_{\alpha \beta \gamma }^{\textrm{tess}})_n$ are the nth-order polynomial density parts of the GP, GV, GGT, and GC of a tesseroid in Cartesian integral kernels, respectively. In order to show the completeness of the expressions for gravitational effects up to the GC, the detailed expressions for a tesseroid in Cartesian integral kernels having a polynomial density model up to Nth-order are presented in Table 1.

The expressions in the second column of Table 1 for the GP, GV, and GGT are the same as those in Eq. (21) of Grombein et al. (2013) and the GC are the same as those in Eqs. (A.11–A.20) of Deng and Shen (2019). It should be noted that low-order gravitational potential gradients (i.e., GP (V), GV ($V_{\alpha }$), and GGT ($V_{\alpha \beta }$) with $\alpha ,\beta$ = x, y, z) presented in Table 1 are consistent with those in Table 2 and Eq. (3) of Lin et al. (2020), although the expressions are slightly different.

Table 1 Detailed expressions for the GP (V), GV ($V_{\alpha }$), GGT ($V_{\alpha \beta }$), and GC ($V_{\alpha \beta \gamma }$) ($\alpha ,\beta ,\gamma = x,y,z$) of a tesseroid in Cartesian integral kernels having a polynomial density model up to Nth-order, where $\ell =\sqrt{r'^2+r^2-2r'r \left( \sin \varphi \sin \varphi '+\cos \varphi \cos \varphi ' \cos (\lambda '-\lambda )\right) }$, $\varDelta _x=r'\left( \cos \varphi \sin \varphi '-\sin \varphi \cos \varphi ' \cos (\lambda '-\lambda ) \right)$, $\varDelta _y=r' \cos \varphi '\sin (\lambda '-\lambda )$, $\varDelta _z=r' \left( \sin \varphi \sin \varphi '+\cos \varphi \cos \varphi ' \cos (\lambda '-\lambda )\right) -r$, and $\kappa _n=r'^{n+2} \cos \varphi '$

2.2 Gravitational effects up to the GC of a spherical shell with arbitrary-order polynomial density

Fig. 2

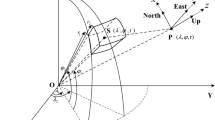
The sectional view of a spherical zonal band revised from Fig. 15 of MacMillan (1930), Fig. 1.1 of Tsoulis (1999), and Fig. E1 of Lin et al. (2020). r and $r'$ are the geocentric distances of the computation point P and integration point, respectively. $\ell$ is the Euclidean distance between the computation point P and integration point. dM is the mass integral element of the spherical zonal band. $\theta$ and $d \theta$ are the spherical distance and its integral element, respectively

The detailed derivation process of analytical expressions for the GP of a spherical shell having a polynomial density model from constant up to cubic order was presented in the electronic supplementary material of Lin et al. (2020). Furthermore, the general expressions for gravitational quantities (i.e., GP, radial GV, radial–radial GGT, and radial–radial–radial GC) and mass of a spherical shell with Nth-order polynomial density are derived in this section.

A spherical zonal band (or a spherical layer in Fig. 15 of MacMillan (1930), Fig. 1.1 of Tsoulis (1999), and a circular ring element in Fig. E1 of Lin et al. (2020)) is shown in Fig. 2. When the spherical distance $\theta$ of a spherical zonal band is integrated from $\theta =0$ to $\pi$, a spherical shell can be obtained (Vaníček et al. 2001, 2004). The formula of the GP of a spherical shell at the computation point P is given as (MacMillan 1930; Tsoulis 1999; Lin et al. 2020):

$$\begin{aligned} V(r)= & {} G \int \limits _{r'=r_1}^{r'=r_2} \int \limits _{\theta =0}^{\theta =\pi } \int \limits _{\alpha =0}^{\alpha =2\pi } \frac{\rho (r') r'^{2} \sin \theta }{\ell } \textrm{d} \alpha \textrm{d} \theta \textrm{d} r' \end{aligned}$$

(12)

$$\begin{aligned} \ell= & {} \sqrt{r^2+r'^2-2 r r' \cos \theta } \end{aligned}$$

(13)

$$\begin{aligned} \frac{\textrm{d} \ell }{\textrm{d} \theta }= & {} \frac{r r' \sin \theta }{\ell } \end{aligned}$$

(14)

where $\rho (r')$ is the polynomial density up to Nth-order of a spherical shell, which is assumed as the same as that of a tesseroid in Eq. (8). $r_1$ and $r_2$ are the inner and outer radii of the spherical shell. $r'\in [r_1,r_2]$ is the geocentric distance, $\alpha \in [0,2\pi ]$ is the azimuth, and $\theta \in [0,\pi ]$ is the spherical distance of the integration point in the local polar coordinate of the spherical coordinate systems. $\ell$ is the Euclidean distance between the computation point P and integration point.

Table 2 Analytical expressions for the GP ($(V^{\textrm{sh}})_n$, $n \ge 0$) of a spherical shell with different nth-order polynomial density parts beginning from constant ($n=0$), where the computation point P is located above ($r>r_2$), inside ($r_1 \le r \le r_2$), and below ($r<r_1$) the spherical shell

Substituting Eqs. (8) and (14) into Eq. (12), the expression for the GP (V(r)) of a spherical shell is simplified as:

$$\begin{aligned} \begin{aligned} V(r)&= \frac{G}{r} \int \limits _{r'=r_1}^{r'=r_2} \int _{\ell _1}^{\ell _2} \int \limits _{\alpha =0}^{\alpha =2\pi } \left( \sum _{n=0}^{N} \rho _n r'^{n+1}\right) \textrm{d} \alpha \textrm{d} \ell \textrm{d} r' \\&= \frac{2\pi G}{r} \int _{r'=r_1}^{r'=r_2} \int \limits _{\ell _1}^{\ell _2} \left( \sum _{n=0}^{N} \rho _n r'^{n+1}\right) \textrm{d} \ell \textrm{d} r' \end{aligned} \end{aligned}$$

(15)

where the computation point P is located above (i.e., $r>r_2$), inside (i.e., $r_1 \le r \le r_2$), and below (i.e., $r<r_1$) the spherical shell. The detailed derivation process of analytical expressions for the GP of a spherical shell is presented in Appendix 1.

Combining Eqs. (47), (48), and (49) in Appendix 1 together, the analytical expressions for the GP (V(r)) of a spherical shell with Nth-order polynomial density can be presented as:

$$\begin{aligned} V(r)= & {} \sum _{n=0}^{N} (V^{\textrm{sh}})_n \nonumber \\= & {} {\left\{ \begin{array}{ll} 4\pi G \sum _{n=0}^{N} \rho _n \frac{(r_2^{n+3}-r_1^{n+3})}{(n+3)r}, &{}r>r_2 \\ 4\pi G \sum _{n=0}^{N} \rho _n \bigg [ \frac{r_2^{n+2}}{n+2} - \frac{r^{n+2}}{(n+2)(n+3)} - \frac{r_1^{n+3}}{(n+3)r} \bigg ], &{}r_1 \le r \le r_2\\ 4\pi G \sum _{n=0}^{N} \rho _n \frac{ (r_2^{n+2}-r_1^{n+2})}{n+2}, &{} r<r_1 \end{array}\right. }\nonumber \\ \end{aligned}$$

(16)

where the analytical expressions for the GP of a spherical shell with different nth-order polynomial density parts beginning from constant (i.e., $(V^{\textrm{sh}})_n$ with $n=0,1,2,3,...,N$) are listed in Table 2 to reveal the detailed variation of the polynomial density parts.

By performing the differentiation with respect to the geocentric distance r of the computation point at one, two, and three times on the analytical expressions for the GP (V(r)) of a spherical shell in Eq. (16), the analytical expressions for radial GV ($V_{z}(r)$), radial–radial GGT ($V_{zz}(r)$), and radial–radial–radial GC ($V_{zzz}(r)$) of a spherical shell with Nth-order polynomial density are derived as:

$$\begin{aligned} V_z(r){} & {} = \sum _{n=0}^{N} (V_{z}^{\textrm{sh}})_n \nonumber \\{} & {} = \left\{ \begin{aligned}&- 4 \pi G \sum _{n=0}^{N} \rho _{n} \frac{(r^{n+3}_2-r_1^{n+3})}{(n+3)r^2} ,&r>r_2 \\&- 4 \pi G \sum _{n=0}^{N} \rho _{n} \frac{(r^{n+3}-r_1^{n+3})}{(n+3)r^2} ,&r_1 \le r \le r_2\\&0 ,&r<r_1 \end{aligned} \right. \nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned} V_{zz}(r){} & {} = \sum _{n=0}^{N} (V_{zz}^{\textrm{sh}})_n \nonumber \\{} & {} = \left\{ \begin{aligned}&8 \pi G \sum _{n=0}^{N} \rho _{n} \frac{r^{n+3}_2-r_1^{n+3}}{(n+3)r^3} ,&r>r_2 \\&- 4 \pi G \sum _{n=0}^{N} \rho _{n} \frac{(n+1)r^{n+3}+2 r_1^{n+3}}{(n+3)r^3},&r_1< r< r_2\\&0 ,&r<r_1 \end{aligned} \right. \nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} V_{zzz}(r){} & {} = \sum _{n=0}^{N} (V_{zzz}^{\textrm{sh}})_n \nonumber \\{} & {} = \left\{ \begin{aligned}&-24 \pi G \sum _{n=0}^{N} \rho _{n} \frac{r^{n+3}_2-r_1^{n+3}}{(n+3)r^4} ,&r>r_2 \\&- 4 \pi G \sum _{n=0}^{N} \rho _{n} \frac{n(n+1)r^{n+3} - 6 r_1^{n+3}}{(n+3)r^4} ,&r_1< r< r_2\\&0 ,&r<r_1 \end{aligned} \right. \nonumber \\ \end{aligned}$$

(19)

where the analytical expressions for radial GV, radial–radial GGT, and radial–radial–radial GC of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{z}^{\textrm{sh}})_n$, $(V_{zz}^{\textrm{sh}})_n$, and $(V_{zzz}^{\textrm{sh}})_n$ with $n=0,1,2,3,...,N$) are similarly listed in Tables 3, 4, and 5, respectively.

Table 3 Analytical expressions for radial GV of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{z}^{\textrm{sh}})_n$)

Table 4 Analytical expressions for radial–radial GGT of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{zz}^{\textrm{sh}})_n$), where the computation point P is located above ($r>r_2$), inside ($r_1<r<r_2$), and below ($r<r_1$) the spherical shell

Table 5 Analytical expressions for radial–radial–radial GC of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{zzz}^{\textrm{sh}})_n$)

The nonzero components of the GGT (i.e., $V_{xx}(r)$, $V_{yy}(r)$, and $V_{zz}(r)$) and GC (i.e., $V_{xxz}(r)$, $V_{yyz}(r)$, and $V_{zzz}(r)$) satisfy Laplace’s equation with the computation point locating above and below the spherical shell (i.e., $r>r_2$ and $r<r_1$) in Eqs. (20–21) Poisson’s equation, and Laplace’s equation with the computation point locating inside the spherical shell (i.e., $r_1< r < r_2$) in Eqs. (22–23) as:

$$\begin{aligned}{} & {} V_{xx}(r) + V_{yy}(r) + V_{zz}(r) =0 \end{aligned}$$

(20)

$$\begin{aligned}{} & {} V_{xxz}(r) + V_{yyz}(r) + V_{zzz}(r) =0 \end{aligned}$$

(21)

$$\begin{aligned}{} & {} V_{xx}(r) + V_{yy}(r) + V_{zz}(r) = -4 \pi G \sum _{n=0}^{N} \rho _n \end{aligned}$$

(22)

$$\begin{aligned}{} & {} V_{xxz}(r) + V_{yyz}(r) + V_{zzz}(r) = 0 \end{aligned}$$

(23)

where $V_{xx}(r) = V_{yy}(r)$ and $V_{xxz}(r) = V_{yyz}(r)$.

Substituting Eqs. (18–19) into Eqs. (20–23), the analytical expressions for other nonzero components of the GGT and GC of a spherical shell with Nth-order polynomial density are presented as:

$$\begin{aligned}{} & {} V_{xx}(r) = V_{yy}(r) = \sum _{n=0}^{N} (V_{xx}^{\textrm{sh}})_n = \sum _{n=0}^{N} (V_{yy}^{\textrm{sh}})_n \nonumber \\{} & {} \quad = {\left\{ \begin{array}{ll} - 4 \pi G \sum _{n=0}^{N} \rho _{n} \frac{r^{n+3}_2-r_1^{n+3}}{(n+3)r^3}, &{} r>r_2 \\ 2 \pi G \sum _{n=0}^{N} \rho _{n} \bigg [\frac{(n+1)r^{n+3}+2 r_1^{n+3}}{(n+3)r^3}-1 \bigg ],&{} r_1<r<r_2\\ 0, &{}r<r_1 \end{array}\right. } \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned}{} & {} V_{xxz}(r) = V_{yyz}(r) = \sum _{n=0}^{N} (V_{xxz}^{\textrm{sh}})_n = \sum _{n=0}^{N} (V_{yyz}^{\textrm{sh}})_n \nonumber \\{} & {} \quad = {\left\{ \begin{array}{ll} 12 \pi G \sum _{n=0}^{N} \rho _{n} \frac{r^{n+3}_2-r_1^{n+3}}{(n+3)r^4}, &{} r>r_2 \\ 2 \pi G \sum _{n=0}^{N} \rho _{n} \frac{n(n+1)r^{n+3} - 6 r_1^{n+3}}{(n+3)r^4}, &{} r_1< r< r_2\\ 0, &{} r<r_1 \end{array}\right. } \nonumber \\ \end{aligned}$$

(25)

where the analytical expressions for other nonzero GGT and GC of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{xx}^{\textrm{sh}})_n=(V_{yy}^{\textrm{sh}})_n$ and $(V_{xxz}^{\textrm{sh}})_n = (V_{yyz}^{\textrm{sh}})_n$ with $n=0,1,2,3,...,N$) are listed in Tables 6 and 7, respectively.

When the computation is located on the top (i.e., $r=r_2$) or bottom (i.e., $r=r_1$) of the spherical shell, there are discontinuities as the density jumps. Regarding the GP component V in Eq. (16) or Table 2 and GV component $V_{z}$ in Eq. (17) or Table 3, $r=r_2$ and $r=r_1$ are applied for the situation where the computation point is inside the spherical shell (i.e., $r_1 \le r \le r_2$) (Fukushima 2018a, Eqs. (46) and(47)). For the GGT components ($V_{zz}$ in Eq. (18) and Table 4; $V_{xx}$ and $V_{yy}$ in Eq. (24) and Table 6) and GC components ($V_{zzz}$ in Eq. (19) and Table 5; $V_{xxz}$ and $V_{yyz}$ in Eq. (25) and Table 7), the computation point that is located on the top or bottom of the spherical shell is slightly moved inside the spherical shell. This strategy is the same as that in Fukushima (2018a). In detail, the geocentric distance r of the computation point when it is on the top ($r_{\textrm{top}}$) or bottom ($r_{\textrm{bottom}}$) of the spherical shell can be presented as:

$$\begin{aligned} r_{\textrm{top}}= & {} R + (1 - \epsilon ) (r_2 - R) \end{aligned}$$

(26)

$$\begin{aligned} r_{\textrm{bottom}}= & {} R + (1 + \epsilon ) (r_1 - R) \end{aligned}$$

(27)

where R is the radius of the reference sphere. $\epsilon$ is the machine epsilon as $\epsilon = 2^{-53} \approx 1.11 \times 10^{-16}$ for double precision and $\epsilon = 2^{-113} \approx 9.63 \times 10^{-35}$ for quadruple precision (Fukushima 2012, 2018a).

Table 6 Analytical expressions for other nonzero gravity gradient tensor of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{xx}^{\textrm{sh}})_n = (V_{yy}^{\textrm{sh}})_n$)

Table 7 Analytical expressions for other nonzero gravitational curvatures of a spherical shell with different nth-order polynomial density parts (i.e., $(V_{xxz}^{\textrm{sh}})_n=(V_{yyz}^{\textrm{sh}})_n$)

Another strategy to treat the special condition of the computation point located on the top of the spherical shell is to move the computation point 1 m above the spherical shell for the evaluation of the GGT components (Kuhn and Hirt 2016; Lin et al. 2020). This strategy can also be applied to the GC components of this special condition.

Furthermore, the general formula of the mass for a spherical shell with Nth-order polynomial density is provided as:

$$\begin{aligned} \begin{aligned} M&= \sum \limits _{n=0}^{N} (M^{\textrm{sh}})_n =\int \limits _{r'=r_1}^{r'=r_2} \int \limits _{\theta =0}^{\theta =\pi } \int \limits _{\alpha =0}^{\alpha =2\pi } \sum _{n=0}^{N} \rho _n r'^{n+2} \sin \theta \textrm{d} \alpha \textrm{d} \theta \textrm{d} r' \\&= 4 \pi \sum _{n=0}^{N} \rho _n \int \limits _{r'=r_1}^{r'=r_2} r'^{n+2} \textrm{d} r' = 4 \pi \sum _{n=0}^{N} \rho _n \frac{r_2^{n+3}-r_1^{n+3}}{n+3} \end{aligned} \end{aligned}$$

(28)

where the formulae of the mass for a spherical shell with different nth-order polynomial density parts (i.e., $(M^{\textrm{sh}})_n$) are listed in Table 8. The expressions for the $(M^{\textrm{sh}})_0$, $(M^{\textrm{sh}})_1$, $(M^{\textrm{sh}})_2$, and $(M^{\textrm{sh}})_3$ in Table 8 are the same as those in Eqs. (E6b), (E7b), (E8b), and (E9b) of Lin et al. (2020), respectively.

Table 8 Expressions for the mass of a spherical shell with nth-order polynomial density parts (i.e., $(M^{\textrm{sh}})_n$)

When the computation point P is outside the spherical shell (i.e., $r>r_2$), the relation between Eq. (28) and Eqs. (16–19) can be found as:

$$\begin{aligned} V(r)= & {} \frac{1}{r} \textrm{G M} \end{aligned}$$

(29)

$$\begin{aligned} V_z(r)= & {} - \frac{1}{r^2} \textrm{G M} \end{aligned}$$

(30)

$$\begin{aligned} V_{zz}(r)= & {} \frac{2}{r^3} \textrm{G M} \end{aligned}$$

(31)

$$\begin{aligned} V_{zzz}(r)= & {} -\frac{6}{r^4} \textrm{G M} \end{aligned}$$

(32)

Based on Eqs. (30–32), the general relation between the radial gravitational effects ($V_t(r)$) up to arbitrary-order and the mass (M) of a spherical shell with Nth-order polynomial density where the computation point P is above the spherical shell (i.e., $r>r_2$) is derived as:

$$\begin{aligned} V_t(r)= & {} \frac{\partial ^t (1/r)}{\partial r^t} \textrm{G M} \nonumber \\{} & {} = \Big [(-1)(-2)(-3)...(-t)\Big ]\frac{1}{r^{t+1}} \textrm{G M}\nonumber \\{} & {} = \frac{(-1)^t\ t!}{r^{t+1}} \textrm{G M} \end{aligned}$$

(33)

where t is the nonzero positive integer (i.e., $t=1,2,3,...$), which means the number of derivation in the radial direction of the computation point.

Table 9 Consistent expressions for the GP, GV, GGT, and GC between this paper and previous papers

Table 10 Numerical values of the parameters of the spherical shell and tesseroid in the numerical experiments

In this section, the work goes beyond the previously cited studies (MacMillan 1930; Tsoulis 1999; Deng and Shen 2018a; Lin et al. 2020) in that we derive the general analytical expressions for the GP (V(r) in Eq. (16) and Table 2), radial GV ($V_z(r)$ in Eq. (17) and Table 3), nonzero GGT ($V_{xx}(r)$, $V_{yy}(r)$ in Eq. (24) and Table 6, and $V_{zz}(r)$ in Eq. (18) and Table 4), and nonzero GC ($V_{xxz}(r)$, $V_{yyz}(r)$ in Eq. (25) and Table 7, and $V_{zzz}(r)$ in Eq. (19) and Table 5) of a spherical shell with Nth-order polynomial density when the computation point P is located above, inside, and below the spherical shell. Moreover, the consistent expressions for the GP, GV, GGT, and GC of a spherical shell are listed in Table 9.

The general formula of the mass for a spherical shell having a polynomial density model up to Nth-order is derived in Eq. (28) and Table 8 as well. Moreover, we derive the general relation between the radial gravitational effects up to arbitrary-order and the mass of a spherical shell with Nth-order polynomial density in Eq. (33) when the computation point P is outside the spherical shell.

3 Numerical investigations

In this section, the numerical experiments are performed to investigate the effects of the GC of the tesseroids and spherical shell with the polynomial density up to fourth-order. The setup of the numerical experiments, including numerical strategy, layout, method, and chosen values, is described in Sect. 3.1. The effects of selected numerical density values on the gravitational effects of a spherical shell are investigated in Sect. 3.2. Sections 3.3 and 3.4 examine the effects of the computation point’s height and latitude on the GC with the polynomial density up to the fourth-order.

3.1 Setup of the numerical experiments

In the following experiments, the commonly used numerical strategy of using tesseroids to discretize a whole spherical shell is adopted due to the simple analytical solutions of the gravitational effects of a spherical shell. As the continuous work of Deng and Shen (2018a), the numerical layouts of the experiments are the same as each other. The main difference lies in that the focus of the experiments in this paper is the effect of variable density models on the gravitational effects with the influence of height and latitude. This effect is revealed by the relative errors between the calculated gravitational effects of the discretized tesseroids and the analytical solutions of the gravitational effects of a spherical shell.

Specifically, the relative errors ($(\delta F)_N$) of the tesseroids discretizing the whole spherical shell with Nth-order polynomial density are given in $\log _{10}$ scale, where F represents the function of the nonzero gravitational effects from the GP to GC, i.e., $F=V$, $V_{z}$, $V_{xx}$, $V_{yy}$, $V_{zz}$, $V_{xxz}$, $V_{yyz}$, and $V_{zzz}$. The reference values are the analytical nonzero gravitational effects of a spherical shell, which can be calculated from Tables 2, 3, 4, 5, 6 and 7. The calculated values are the sum of the nonzero gravitational effects of the discretized tesseroids forming the total spherical shell.

Laplace’s equation of the GGT and GC is applied to reveal the internal numerical quality as:

$$\begin{aligned}{} & {} (\delta \varDelta L_1)_N\nonumber \\{} & {} \quad = \log _{10}\Bigg (\varDelta V_{xx} + \varDelta V_{yy} + \varDelta V_{zz}\Bigg ) \nonumber \\{} & {} \quad = \log _{10}\Bigg ( \Bigg | \sum _{n=0}^{N} \Bigg (\sum V_{xx}^{\textrm{tess}}\Bigg )_n + \sum _{n=0}^{N} \Bigg (\sum V_{yy}^{\textrm{tess}}\Bigg )_n\nonumber \\{} & {} \qquad + \sum _{n=0}^{N} \Bigg (\sum V_{zz}^{\textrm{tess}}\Bigg )_n \nonumber \\{} & {} \qquad - \sum _{n=0}^{N} (V_{xx}^{\textrm{sh}})_n - \sum _{n=0}^{N} (V_{yy}^{\textrm{sh}})_n - \sum _{n=0}^{N} (V_{zz}^{\textrm{sh}})_n \Bigg | \Bigg )\end{aligned}$$

(34)

$$\begin{aligned}{} & {} (\delta \varDelta L_2)_N = \log _{10}\Bigg (\varDelta V_{xxz} + \varDelta V_{yyz} + \varDelta V_{zzz}\Bigg ) \nonumber \\{} & {} \quad = \log _{10}\Bigg (\Bigg | \sum _{n=0}^{N} \Bigg (\sum V_{xxz}^{\textrm{tess}}\Bigg )_n + \sum _{n=0}^{N} \Bigg (\sum V_{yyz}^{\textrm{tess}}\Bigg )_n \nonumber \\{} & {} \qquad + \sum _{n=0}^{N} \Bigg (\sum V_{zzz}^{\textrm{tess}}\Bigg )_n \nonumber \\{} & {} \quad - \sum _{n=0}^{N} (V_{xxz}^{\textrm{sh}})_n - \sum _{n=0}^{N} (V_{yyz}^{\textrm{sh}})_n - \sum _{n=0}^{N} (V_{zzz}^{\textrm{sh}})_n \Bigg | \Bigg ) \end{aligned}$$

(35)

where $(\delta \varDelta L_1)_N$ and $(\delta \varDelta L_2)_N$ are the Laplace parameters of the GGT and GC with Nth-order polynomial density. They are theoretically equal to zero and denoted as absolute errors in the numerical experiments. In the following experiments, the numerical calculation with respect to relative and absolute errors is performed in quadruple precision.

The 3D Gauss–Legendre quadrature method is applied to obtain the numerical values of gravitational effects up to the GC of the tesseroid in the 3D integral forms in Table 1. The general expression for 3D Gauss–Legendre quadrature method is given as (Wild-Pfeiffer 2008; Uieda et al. 2016; Deng and Shen 2018b; Lin et al. 2020):

$$\begin{aligned} F\approx & {} \frac{(r_2-r_1)(\varphi _2-\varphi _1)(\lambda _2-\lambda _1)}{8} \nonumber \\{} & {} \sum _{k=1}^{N^r} \sum _{j=1}^{N^{\varphi }} \sum _{i=1}^{N^{\lambda }} W_i^{\lambda } W_j^{\varphi } W_k^{r} I(\lambda _i, \varphi _j, r_k) \end{aligned}$$

(36)

$$\begin{aligned} \lambda _i= & {} \frac{x_i(\lambda _2-\lambda _1)+(\lambda _2+\lambda _1)}{2} \end{aligned}$$

(37)

$$\begin{aligned} \varphi _j= & {} \frac{x_j(\varphi _2-\varphi _1)+(\varphi _2+\varphi _1)}{2} \end{aligned}$$

(38)

$$\begin{aligned} r_k= & {} \frac{x_k(r_2-r_1)+(r_2+r_1)}{2} \end{aligned}$$

(39)

where F means the function of detailed expressions for gravitational effects up to the GC in Table 1. $I(\lambda _i, \varphi _j, r_k)$ denotes the function of detailed integral kernels of gravitational effects up to the GC in Table 1. $[\lambda _1,\lambda _2]\times [\varphi _1,\varphi _2]\times [r_1,r_2]$ is the integration domain; $N_{\lambda }$, $N_{\varphi }$, and $N_r$ are the integer degrees; $W_i^{\lambda }$, $W_j^{\varphi }$, and $W_k^{r}$ are the weights; $x_i$, $x_j$, and $x_k$ are the nodes with respect to the longitude, latitude, and radial directions, respectively. With larger degrees, better computational accuracy can be obtained, whereas the computation time will be longer. Based on Sect. 4.2 of Deng and Shen (2018b), the degrees of $N_{\lambda }$, $N_{\varphi }$, and $N_r$ are chosen as 2, 2, and 2 to present the acceptable numerical results at the height of 260 km, and related weights and nodes can be referred in Table 4 of Wild-Pfeiffer (2008) and Table 5 of Deng and Shen (2018b).

The numerical values of the parameters of the spherical shell and tesseroid are listed in Table 10. It should be noted that the constant density of the spherical shell and tesseroid is the same as each other as $\rho _0=2670\ \mathrm {kg\ m^{-3}}$, which is often assumed as the mean density for the topography of the earth (Heiskanen and Moritz 1967; Hinze 2003; Tenzer et al. 2021).

3.2 Effects of density values on gravitational effects of a spherical shell

Fig. 3

Visualization of the reference values in $\log _{10}$ scale for the GP ($(V^{\textrm{sh}})_0$ blue curve), radial GV ($(V_z^{\textrm{sh}})_0$ red curve), radial–radial GGT ($(V_{zz}^{\textrm{sh}})_0$ green curve), and radial–radial–radial GC ($(V_{zzz}^{\textrm{sh}})_0$ purple curve) of a spherical shell using the constant density $\rho _0=2670\ \mathrm {kg\ m^{-3}}$ with the influence of the height $h\in [0, 300]$ km with an interval of 1 km

The chosen numerical values of the density coefficient $\rho _n$ in the different expressions for gravitational effects (e.g., V, $V_z$, $V_{zz}$, and $V_{zzz}$) of a spherical shell and tesseroid are important for the evaluation of the gravitational effects of a spherical shell and tesseroid. Due to the analytical solutions of the gravitational effects of a spherical shell as the reference values for discretized tesseroids, the effects of density values on the gravitational effects of a spherical shell are investigated in this section.

In the numerical experiments, the values of gravitational effects of a spherical shell with the chosen density coefficient $\rho _n$ ($n\ge 1$) are assumed to be at the same level as these of a spherical shell with the constant density $\rho _0=2670\ \mathrm {kg\ m^{-3}}$. The numerical values of the parameters of the spherical shell are shown in Table 10. The computation point P is located above the spherical shell (i.e., $r>r_2$) with the height $h\in [0, 300]$ km using an interval of 1 km. The relation between geocentric distance r and height h of the computation point P is $r=R+h$, where R is the radius of the reference sphere and equal to the outer radius of the spherical shell $r_2$ in Table 10. In other words, the spherical case is adopted.

Table 11 Statistic information of the reference values in $\log _{10}$ scale of the GP $(V^{\textrm{sh}})_0$, radial GV $(V_z^{\textrm{sh}})_0$, radial–radial GGT $(V_{zz}^{\textrm{sh}})_0$, and radial–radial–radial GC $(V_{zzz}^{\textrm{sh}})_0$ of a spherical shell with constant density $\rho _0$ in Fig. 3

Table 12 Mean values in $\log _{10}$ scale of gravitational potential $(V^{\textrm{sh}})_1$, radial gravity vector $(V_z^{\textrm{sh}})_1$, radial–radial gravity gradient tensor $(V_{zz}^{\textrm{sh}})_1$, and radial–radial–radial gravitational curvatures $(V_{zzz}^{\textrm{sh}})_1$ of a spherical shell with linear density coefficient $\rho _1=\rho _0\times 10^{-m}$ $(m\in [2, 4, 6, 8])$, where the unit of $\rho _1$ is $\mathrm {kg\ m^{-4}}$ and the values are truncated to one decimal place

Table 13 Mean values in $\log _{10}$ scale of gravitational potential $(V^{\textrm{sh}})_2$, radial gravity vector $(V_z^{\textrm{sh}})_2$, radial–radial gravity gradient tensor $(V_{zz}^{\textrm{sh}})_2$, and radial–radial–radial gravitational curvatures $(V_{zzz}^{\textrm{sh}})_2$ of a spherical shell with quadratic density coefficient $\rho _2=\rho _0\times 10^{-m}$ $(m\in [10, 12, 14, 16])$, where the unit of $\rho _2$ is $\mathrm {kg\ m^{-5}}$ and the values are truncated to one decimal place

Table 14 Mean values in $\log _{10}$ scale of gravitational potential $(V^{\textrm{sh}})_3$, radial gravity vector $(V_z^{\textrm{sh}})_3$, radial–radial gravity gradient tensor $(V_{zz}^{\textrm{sh}})_3$, and radial–radial–radial gravitational curvatures $(V_{zzz}^{\textrm{sh}})_3$ of a spherical shell with cubic density coefficient $\rho _3=\rho _0\times 10^{-m}$ $(m\in [18, 20, 22, 24])$, where the unit of $\rho _3$ is $\mathrm {kg\ m^{-6}}$ and the values are truncated to one decimal place

Table 15 Mean values in $\log _{10}$ scale of gravitational potential $(V^{\textrm{sh}})_4$, radial gravity vector $(V_z^{\textrm{sh}})_4$, radial–radial gravity gradient tensor $(V_{zz}^{\textrm{sh}})_4$, and radial–radial–radial gravitational curvatures $(V_{zzz}^{\textrm{sh}})_4$ of a spherical shell with quartic density coefficient $\rho _4=\rho _0\times 10^{-m}$ $(m\in [26, 28, 30, 32])$, where the unit of $\rho _4$ is $\mathrm {kg\ m^{-7}}$ and the values are truncated to one decimal place

Substituting the above numerical values into the first expressions with the constant density $\rho _{0}$ when the computation point is located above the spherical shell in Tables 2, 34 and 5, the values of the GP $(V^{\textrm{sh}})_0$, radial GV $(V_z^{\textrm{sh}})_0$, radial–radial GGT $(V_{zz}^{\textrm{sh}})_0$, and radial–radial–radial GC $(V_{zzz}^{\textrm{sh}})_0$ of a spherical shell using the constant density $\rho _0$ with the influence of the height are obtained and illustrated in $\log _{10}$ scale in Fig. 3. In Fig. 3, the x-axis means the height h of the computation point above the reference sphere. The y-axis means the reference values in $\log _{10}$ scale of the GP ($(V^{\textrm{sh}})_0$), radial GV ($(V_z^{\textrm{sh}})_0$), radial–radial GGT ($(V_{zz}^{\textrm{sh}})_0$), and radial–radial–radial GC ($(V_{zzz}^{\textrm{sh}})_0$) of a spherical shell using the constant density $\rho _0=2670\ \mathrm {kg\ m^{-3}}$. Meanwhile, the related statistic information (i.e., minimum, maximum, mean, and variance) of gravitational effects is shown in Table 11, where the units of $(V^{\textrm{sh}})_0$, $(V_z^{\textrm{sh}})_0$, $(V_{zz}^{\textrm{sh}})_0$, and $(V_{zzz}^{\textrm{sh}})_0$ are $\mathrm {m^2\ s^{-2}}$, $\mathrm {m \ s^{-2}}$, $\mathrm {s^{-2}}$, and $\mathrm {m^{-1}\ s^{-2}}$, respectively.

From Fig. 3, with the increased heights, the reference values of the $(V^{\textrm{sh}})_0$, $(V_z^{\textrm{sh}})_0$, $(V_{zz}^{\textrm{sh}})_0$, and $(V_{zzz}^{\textrm{sh}})_0$ of a spherical shell with the constant density are gradually getting smaller. The statistic information in Table 11 reveals that the ranges of the values of the $(V^{\textrm{sh}})_0$, $(V_z^{\textrm{sh}})_0$, $(V_{zz}^{\textrm{sh}})_0$, and $(V_{zzz}^{\textrm{sh}})_0$ in $\log _{10}$ scale are small especially with the small variances. Consequently, the magnitude of the numerical results for the spherical shell in Fig. 3 is stable, and they can be used as the reference values for the calculated values of the tesseroids in the following numerical experiments.

Furthermore, the mean values in Table 11 using the constant density $\rho _0$ are set as the reference values. In other words, by changing the density coefficients $\rho _1$, $\rho _2$, $\rho _3$, and $\rho _4$ at the level of $\rho _0\times 10^{-m}$ ($m\ge 1$), the values of different gravitational effects of a spherical shell can be obtained to reach the same level as the mean values using the constant density $\rho _0$ in Table 11.

The mean values in $\log _{10}$ scale of the GP (i.e., $(V^{\textrm{sh}})_1$, $(V^{\textrm{sh}})_2$, $(V^{\textrm{sh}})_3$, and $(V^{\textrm{sh}})_4$), radial GV (i.e., $(V_z^{\textrm{sh}})_1$, $(V_z^{\textrm{sh}})_2$, $(V_z^{\textrm{sh}})_3$, and $(V_z^{\textrm{sh}})_4$), radial–radial GGT (i.e., $(V_{zz}^{\textrm{sh}})_1$, $(V_{zz}^{\textrm{sh}})_2$, $(V_{zz}^{\textrm{sh}})_3$, and $(V_{zz}^{\textrm{sh}})_4$), and radial–radial–radial GC (i.e., $(V_{zzz}^{\textrm{sh}})_1$, $(V_{zzz}^{\textrm{sh}})_2$, $(V_{zzz}^{\textrm{sh}})_3$, and $(V_{zzz}^{\textrm{sh}})_4$) of a spherical shell with linear, quadratic, cubic, and quartic density coefficients (i.e., $\rho _1$, $\rho _2$, $\rho _3$, and $\rho _4$) are listed in Tables 12, 13, 14, and 15, respectively.

Regarding the mean values in $\log _{10}$ scale between Tables 11, 12, 13, 14 and 15 to reach the level of mean values for different gravitational effects in Table 11, the ranges of density coefficients $\rho _1$, $\rho _2$, $\rho _3$, and $\rho _4$ are in about [$\rho _0\times 10^{-7}$, $\rho _0\times 10^{-6}$], [$\rho _0\times 10^{-14}$, $\rho _0\times 10^{-13}$], [$\rho _0\times 10^{-21}$, $\rho _0\times 10^{-20}$], and [$\rho _0\times 10^{-28}$, $\rho _0\times 10^{-27}$], respectively. It can be found that the difference of the magnitude among the ranges is at the level of $-7$, i.e., $-14-(-7)=-7$ between $\rho _1$ and $\rho _2$, $-21-(-14)=-7$ between $\rho _2$ and $\rho _3$, and $-28-(-21)=-7$ between $\rho _3$ and $\rho _4$. In other words, the order of magnitude decreases with 1/r in the spherical case.

Herein, the relation between $\rho _n$ ($n\ge 0$) and $\rho _0$ is theoretically derived. The initial assumption is that the nonzero gravitational effects (i.e., $(V^{\textrm{sh}})_n$, $(V^{\textrm{sh}}_z)_n$, $(V^{\textrm{sh}}_{xx})_n$, $(V^{\textrm{sh}}_{yy})_n$, $(V^{\textrm{sh}}_{zz})_n$, $(V^{\textrm{sh}}_{xxz})_n$, $(V^{\textrm{sh}}_{yyz})_n$, and $(V^{\textrm{sh}}_{zzz})_n$) of a spherical shell with different nth-order polynomial density parts in Tables 2, 3, 4, 5, 6 and 7 are equal when the computation point is located above the spherical shell. The physical meaning of this assumption is the uniform equality of the polynomial density parts. It helps to understand the magnitude of each term of the polynomial density. The formulae of this assumption can be expressed as:

$$\begin{aligned} (V^{\textrm{sh}})_0= & {} \frac{4 \pi G \rho _{0} (r^{3}_2-r_1^{3})}{3r} \nonumber \\= & {} \frac{4 \pi G \rho _{n} (r^{n+3}_2-r_1^{n+3})}{(n+3)r} = (V^{\textrm{sh}})_n \end{aligned}$$

(40)

$$\begin{aligned} (V_z^{\textrm{sh}})_0= & {} \frac{- 4 \pi G \rho _0 (r^{3}_2-r_1^{3})}{3r^2} \nonumber \\= & {} \frac{- 4 \pi G \rho _{n} (r^{n+3}_2-r_1^{n+3})}{(n+3)r^2} = (V_z^{\textrm{sh}})_n \end{aligned}$$

(41)

$$\begin{aligned} (V_{xx}^{\textrm{sh}})_0= & {} (V_{yy}^{\textrm{sh}})_0 = \frac{-4 \pi G \rho _{0} (r^{3}_2-r_1^{3})}{3 r^3} \nonumber \\= & {} \frac{-4 \pi G \rho _{n} (r^{n+3}_2-r_1^{n+3})}{(n+3)r^3} = (V_{xx}^{\textrm{sh}})_n = (V_{yy}^{\textrm{sh}})_n \nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned} (V_{zz}^{\textrm{sh}})_0= & {} \frac{8 \pi G \rho _{0} (r^{3}_2-r_1^{3})}{3 r^3} \nonumber \\= & {} \frac{8 \pi G \rho _{n} (r^{n+3}_2-r_1^{n+3})}{(n+3)r^3} = (V_{zz}^{\textrm{sh}})_n \end{aligned}$$

(43)

$$\begin{aligned} (V_{xxz}^{\textrm{sh}})_0= & {} (V_{yyz}^{\textrm{sh}})_0 = \frac{4 \pi G \rho _{0} (r^{3}_2-r_1^{3})}{r^4} \nonumber \\= & {} \frac{12 \pi G \rho _{n} (r^{n+3}_2-r_1^{n+3})}{(n+3)r^4} = (V_{xxz}^{\textrm{sh}})_n = (V_{yyz}^{\textrm{sh}})_n \nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned} (V_{zzz}^{\textrm{sh}})_0= & {} \frac{-8 \pi G \rho _{0} (r^{3}_2-r_1^{3})}{r^4} \nonumber \\= & {} \frac{-24 \pi G \rho _{n} (r^{n+3}_2-r_1^{n+3})}{(n+3)r^4} = (V_{zzz}^{\textrm{sh}})_n \end{aligned}$$

(45)

After simplifying Eqs. (40–45), the relation between $\rho _n$ ($n\ge 0$) and $\rho _0$ is obtained as:

$$\begin{aligned} \rho _n = \rho _0 \frac{(n+3)(r_2^3-r_1^3)}{3(r_2^{n+3}-r_1^{n+3})} \end{aligned}$$

(46)

where this same relation exists for the mass of a spherical shell with different nth-order polynomial density parts if $M^{\textrm{sh}}_0=M^{\textrm{sh}}_n$ in Table 8.

Regarding Eq. (46), once the values of inner and outer radii (i.e., $r_1$ and $r_2$) of the spherical shell are known, the numerical relation between $\rho _n$ and $\rho _0$ can be obtained. Substituting the values of $r_1$ and $r_2$ in Table 10 into Eq. (46), the relation between $\rho _n$ ($n=1,2,3,4$) and $\rho _0$ is listed in Table 16. The coefficients in Table 16 are in the ranges of [$\rho _0\times 10^{-7}$, $\rho _0\times 10^{-6}$], [$\rho _0\times 10^{-14}$, $\rho _0\times 10^{-13}$], [$\rho _0\times 10^{-21}$, $\rho _0\times 10^{-20}$], and [$\rho _0\times 10^{-28}$, $\rho _0\times 10^{-27}$] for density coefficients $\rho _1$, $\rho _2$, $\rho _3$, and $\rho _4$ presented in Tables 12, 13, 14 and 15. Regarding the following experiments in Sects. 3.3 and 3.4, the numerical density coefficients are set according to the formula in Eq. (46) in quadruple precision to show the extreme situation that the values of gravitational effects are correspondingly equal due to the different polynomial density parts.

Table 16 Numerical relation between $\rho _n$ ($n=1,2,3,4$) and $\rho _0$ with the values of $r_1$ and $r_2$ in Table 10, where the nonzero gravitational effects of a spherical shell with different nth-order polynomial density parts are equal when the computation point is located above the spherical shell and the values are truncated to one decimal place

3.3 Influence of height on the GC with polynomial density up to fourth-order

Fig. 4

a Visualization of the relative errors in $\log _{10}$ scale of the GP ($(\delta V)_4$ blue curve), radial GV ($(\delta V_z)_4$ red curve), GGT ($(\delta V_{xx})_4$ black curve, $(\delta V_{yy})_4$ green dashed curve, and $(\delta V_{zz})_4$ cyan dotted curve), and GC ($(\delta V_{xxz})_4$ deep-sky-blue curve, $(\delta V_{yyz})_4$ thistle dashed curve, and $(\delta V_{zzz})_4$ magenta dotted curve) with fourth-order polynomial density by a grid size of $15'\times 15'$ with the influence of the height h from the surface 0 to 300 km with an interval of 1 km; b the absolute errors in $\log _{10}$ scale of the Laplace parameters of the GGT ($(\delta \varDelta L_1)_0$ magenta curve, $(\delta \varDelta L_1)_1$ thistle curve, $(\delta \varDelta L_1)_2$ deep-sky-blue curve, $(\delta \varDelta L_1)_3$ orange curve, and $(\delta \varDelta L_1)_4$ yellow curve) and GC ($(\delta \varDelta L_2)_0$ blue curve, $(\delta \varDelta L_2)_1$ red curve, $(\delta \varDelta L_2)_2$ green curve, $(\delta \varDelta L_2)_3$ black curve, and $(\delta \varDelta L_2)_4$ purple curve) using different order polynomial density in quadruple precision with the unit $\mathrm {s^{-2}}$ for $(\delta \varDelta L_1)_N$ and $\mathrm {m^{-1}\ s^{-2}}$ for $(\delta \varDelta L_2)_N$ (i.e., $N=0,1,2,3,4$)

The near-zone problem (or very-near-area problem) of the computation point for the tesseroid mass body (i.e., there are large approximation errors when the computation point approaches the surface of the tesseroid mass body) has been investigated by using tesseroids to discretize the spherical shell for the GP, GV, GGT (Uieda et al. 2016; Shen and Deng 2016), GC (Deng and Shen 2018a, b, 2019), and invariants of the gravity gradient tensor and their first-order derivatives (Deng et al. 2021) with the constant density. Based on the same numerical situation to investigate the influence of the geocentric distance on the GC (Deng and Shen 2018a, Sect.3.3), we extend the constant density to the polynomial density up to fourth-order to reveal the density variation on the effects of the GC using the relative and absolute errors. The GP, GV, and GGT are included for comparison as well.

For the position of the computation point, the height h is chosen as $h\in [0,300]$ km (Lin et al. 2020, Sect. 3.3) with an interval of 1 km and the spherical longitude and latitude are $(0^{\circ }, 0^{\circ })$ (Deng and Shen 2018a, Sect. 3.3). Other numerical values of the spherical shell and tesseroid can be referred to in Table 10.

Due to the same performance of relative errors in $\log _{10}$ scale from zero- up to fourth-order polynomial density, only the relative errors in $\log _{10}$ scale of the GP ($(\delta V)_4$), radial GV ($(\delta V_z)_4$), GGT ($(\delta V_{xx})_4$, $(\delta V_{yy})_4$, and $(\delta V_{zz})_4$), and GC ($(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$) with fourth-order polynomial density with the influence of the height are illustrated in Fig. 4a. The absolute errors in $\log _{10}$ scale of Laplace parameters of the GGT ($(\delta \varDelta L_1)_N$) and GC ($(\delta \varDelta L_2)_N$) from zero- up to fourth-order polynomial density (i.e., $N=0,1,2,3,4$) are presented in Fig. 4b based on Eqs. (34–35).

From Fig. 4a, the relative errors of the GC (i.e., $(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$) are larger than other gravitational effects (i.e., $(\delta V)_4$, $(\delta V_z)_4$, $(\delta V_{xx})_4$, $(\delta V_{yy})_4$, and $(\delta V_{zz})_4$) with the influence of the height at the same numerical situation. Specifically, the relative errors in $\log _{10}$ scale are in the range of about [$-14$, $-4$] for $(\delta V_z)_4$, [$-14$, 0] for $(\delta V_z)_4$, [$-15$, 3] for $(\delta V_{xx})_4$, $(\delta V_{yy})_4$, and $(\delta V_{zz})_4$, and [$-14$, 6] for $(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$. Regarding the general trends of relative errors for different gravitational effects, they decrease with the increased height. For the height below 30 km, there exist turning points because of the sign change of the absolute operation within the logarithmic scale, which are similar to those in Fig. 4a of Deng and Shen (2018a). The ranges of the rapid drop zone, i.e., its relative errors decline rapidly (Deng and Shen 2018b, Sect. 4.4), are below about 110 km for $(\delta V)_4$, 140 km for $(\delta V_z)_4$, 150 km for $(\delta V_{xx})_4$, $(\delta V_{yy})_4$, and $(\delta V_{zz})_4$, and 180 km for $(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$. The concussion zones are found for the GGT ($(\delta V_{xx})_4$ and $(\delta V_{zz})_4$) and GC ($(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$), where the relative errors change with large variation at the range of [150, 170] km for the GGT and [180, 200] km for the GC. In the stable zones, the relative errors in $\log _{10}$ scale are at the level of about $-14$ and $-13$. The relative errors in $\log _{10}$ scale of the GGT and GC are large than 0 below the height of about 24 km and 50 km, respectively.

The ten rough curves in Fig. 4b decrease with the increased height as well. With the polynomial density from zero- to fourth-order (i.e., $N=0,1,2,3,4$), the absolute errors of Laplace parameters of the GC ($(\delta \varDelta L_2)_N$) increase slightly, which are also found for Laplace parameters of the GGT ($(\delta \varDelta L_1)_N$). The reason lies in that as the order of the polynomial density decreases, the superposition effect of absolute errors in Eqs. (34–35) becomes obvious. The ranges of the absolute errors in $\log _{10}$ scale are approximately [$-42$, $-34$] for $(\delta \varDelta L_1)_N$ and [$-47$, $-37$] for $(\delta \varDelta L_2)_N$. Regarding the quadruple precision, its machine epsilon of IEEE 2008 in $\log _{10}$ scale is about $\log _{10}(9.63\times 10^{-35}) \approx -34$ (Fukushima 2012). The ranges of ten rough curves in Fig. 4b in $\log _{10}$ scale are almost below $-34$, which means that the sum of the components of the GGT and GC with different order polynomial density in Eqs. (34–35) satisfied Laplace’s equation under current numerical condition.

The reason for the same performance of relative errors in $\log _{10}$ scale from zero- to fourth-order polynomial density for different gravitational effects using tesseroids to discretize the spherical shell lies in that the assumption of the density coefficient in Eq. (46) of Sect. 3.2. In other words, the same coefficients are cancelled both in the numerator and denominator in the relative errors for different order polynomial density, whereas the absolute errors can reflect the error superposition effect caused by different order polynomial density in Eqs. (34–35), which are revealed under the $\log _{10}$ operation in Fig. 4b.

Furthermore, the existence of the rapid drop zone, especially below the height of 10 km for the GGT and GC in Fig. 4a, shows that the near-zone problem still occurs for different order polynomial density, i.e., the choice of polynomial density model does not affect the existence of the near-zone problem. Solving the near-zone problem will be focused on improving the numerical method for triple (or double) integrals and refined geometrical shape (or grid size) of the tesseroid mass body.

3.4 Influence of latitude on the GC with polynomial density up to fourth order

Fig. 5

a Visualization of the relative errors in $\log _{10}$ scale of the GP ($(\delta V)_4$ blue curve), GV ($(\delta V_z)_4$ red curve), GGT ($(\delta V_{xx})_4$ dark-blue curve, $(\delta V_{yy})_4$ green curve, and $(\delta V_{zz})_4$ yellow curve), and GC ($(\delta V_{xxz})_4$ thistle curve, $(\delta V_{yyz})_4$ deep-sky-blue curve, and $(\delta V_{zzz})_4$ magenta curve) with fourth-order polynomial density by a grid size of $15'\times 15'$ with the influence of the latitude $\varphi$ from 0 to $90^{\circ }$ with an interval of $1^{\circ }$ at the satellite height of $h=260$ km; b the absolute errors in $\log _{10}$ scale of the Laplace parameters of the GGT ($(\delta \varDelta L_1)_N$) and GC ($(\delta \varDelta L_2)_N$) using different order polynomial density (i.e., $N=0,1,2,3,4$), where other parameters are the same as in Fig. 4b

The influence of the computation point’s latitude on the GC of the tesseroid mass body was investigated with the constant density using the spherical integral kernels (Deng and Shen 2018a) and Cartesian integral kernels (Deng and Shen 2018b). Herein, the constant density is extended up to fourth-order polynomial density to study the density variation on the effects of the GC with the influence of latitude using the relative and absolute errors. Meanwhile, the low-order gravitational potential gradients (i.e., GP, GV, and GGT) are also investigated. The latitude variation of the computation point indirectly reveals the effects of the geometrical shape of the tesseroid mass body on the gravitational effects.

The computation point is at the satellite height of $h = 260$ km above the surface of the spherical shell, where the near-zone effects of different gravitational effects are largely reduced as revealed in Fig. 4. The longitude and latitude of the computation point are $\lambda =0^{\circ }$ and $\varphi \in [0^{\circ }, 90^{\circ }]$ with an interval of $1^{\circ }$ because of the spherical symmetry of the spherical shell. Table 10 lists other numerical values of the spherical shell and tesseroid.

Analogously, the relative errors in $\log _{10}$ scale with zero- up to fourth-order polynomial density are the same as each other. Figure 5a only presents the relative errors in $\log _{10}$ scale of the GP ($(\delta V)_4$), GV ($(\delta V_z)_4$), GGT ($(\delta V_{xx})_4$, $(\delta V_{yy})_4$, and $(\delta V_{zz})_4$), and GC ($(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$) with fourth-order polynomial density with the influence of the latitude. Using Eqs. (34–35), Fig. 5b shows the absolute errors in $\log _{10}$ scale of Laplace parameters of the GGT ($(\delta \varDelta L_1)_N$) and GC ($(\delta \varDelta L_2)_N$) using different order polynomial density (i.e., $N=0,1,2,3,4$) with the influence of the latitude.

From Fig. 5a, all the relative errors show the similar rule that as the latitude increases, the relative errors increase as well, especially in the polar region (i.e., $\sim 80^{\circ } \le \varphi \le 90^{\circ }$). There are a decreased turning point for $(\delta V_{yyz})_4$ at about $\varphi \approx 44^{\circ }$ and other decreased turning points for other gravitational effects in the polar region due to the absolute operation of the sign change inside the logarithmic scale. The ranges of the relative errors in $\log _{10}$ scale are about [$-14$, $-9$] for $(\delta V)_4$, [$-14$, $-7$] for $(\delta V_z)_4$, [$-14$, $-5$] for $(\delta V_{xx})_4$, $(\delta V_{yy})_4$, and $(\delta V_{zz})_4$, and [$-14$, $-3$] for $(\delta V_{xxz})_4$, $(\delta V_{yyz})_4$, and $(\delta V_{zzz})_4$.

Although the curves between Fig. 5a and Fig. 8 of Deng and Shen (2018a) are similar, it should be noted that there are some differences between them. Firstly, the coordinate system of gravitational effects in Fig. 5a is the local north-oriented frame system with x, y, z pointing to the north, east, and radial up and in Fig. 8 of Deng and Shen (2018a) is the local East-North-Up topocentric reference system with x, y, z pointing to the east, north, and radial up. In other words, $(\delta V_{xx})_4$, $(\delta V_{yy})_4$, $(\delta V_{xxz})_4$, and $(\delta V_{yyz})_4$ in Fig. 5a are correspondingly with respect to GGT_$\delta V_{yy}$, GGT_$\delta V_{xx}$, GC_$\delta V_{yyz}$, and GC_$\delta V_{xxz}$ in Fig. 8 of Deng and Shen (2018a). Secondly, there are no gaps for $(\delta V_{yy})_4$ and $(\delta V_{yyz})_4$ at latitude $\varphi =90^{\circ }$ in Fig. 5a, whereas the curves of the $GGT\_\delta V_{xx}$ and $GC\_\delta V_{xxz}$ have gaps at latitude $\varphi =90^{\circ }$ in Fig. 8 of Deng and Shen (2018a). The reason is that the tesseroid formulae of the GGT and GC in this paper are in Cartesian integral kernels, whereas they were in spherical integral kernels in Deng and Shen (2018a). Using Cartesian integral kernels can avoid the gap at the polar point (i.e., the polar-singularity problem). Thirdly, the curve of the $(\delta V_{yyz})_4$ is smooth at the low latitude region (i.e., $\varphi < 44^{\circ }$) in Fig. 5a, whereas the GC_$\delta V_{xxz}$ has a slightly rough curve at the same low latitude region. Fourthly, the numerical methods are Gauss–Legendre quadrature with 3D degrees (2, 2, 2) for Fig. 5 in this section and Taylor series expansion with a second-order for Fig. 8 of Deng and Shen (2018a). Finally, Fig. 5 in this section adopts the fourth-order polynomial density model, whereas Fig. 8 of Deng and Shen (2018a) applied the constant density.

Regarding Fig. 5b, the ten curves of the absolute errors in $\log _{10}$ scale do not change particularly as the latitude rises. Similar superposition effects of absolute errors both for Laplace parameters of the GGT ($(\delta \varDelta L_1)_N$) and GC ($(\delta \varDelta L_2)_N$) are obvious as the increased polynomial density from zero- to fourth-order. The absolute errors in $\log _{10}$ scale are in ranges of about [$-42$, $-39$] for $(\delta \varDelta L_1)_N$ and [$-46$, $-43$] for $(\delta \varDelta L_2)_N$, which are all below the machine epsilon of quadruple precision in $\log _{10}$ scale as $-34$. It can be confirmed that under the current numerical condition, the components of the GGT and GC with zero- up to fourth-order polynomial density in Eqs. (34–35) satisfy Laplace’s equation at the satellite height of $h=260$ km.

4 Conclusions and outlooks

In recent years, the research trends in gravity field modeling have been from constant to variable density and from low-order to higher-order gravitational potential gradients (e.g., the GC). In this contribution, the formulae of the GC of a tesseroid and spherical shell are extended from constant density to arbitrary-order polynomial density. In detail, the general expression for the GC of a tesseroid with Nth-order polynomial density is derived in Cartesian integral kernel, and the detailed components of the GC are presented in the spherical coordinate system. The general analytical expressions for gravitational effects up to the GC of a spherical shell with Nth-order polynomial density are derived when the computation point is located above, inside, and below the spherical shell. Meanwhile, the general formula of the mass for a spherical shell having a polynomial density model up to Nth-order is derived. Furthermore, we derive the general relation between radial gravitational effects up to arbitrary-order and the mass of a spherical shell with Nth-order polynomial density with the computation point located above the spherical shell.

Under the assumption that the nonzero gravitational effects of a spherical shell with different nth-order polynomial density parts are equal when the computation point is located above the spherical shell, the effects of density values on gravitational effects up to the GC of a spherical shell are investigated. The relation between the constant density $\rho _0$ and density coefficient $\rho _n$ ($n\ge 0$) is derived. The difference of the magnitude between the density coefficients $\rho _n$ and $\rho _{n+1}$ is about at the level of $-7$.

The influence of the computation point’s height on gravitational effects up to the GC with polynomial density up to fourth-order is investigated. Numerical experiments show that the near-zone problem occurs for the GC with different order polynomial density. In other words, the change in density does not affect the existence of the near-zone problem. The relative errors in $\log _{10}$ scale of the GGT and GC are large than 0 below the height of about 24 km and 50 km, respectively. The key to solving the near-zone problem of the GC of the tesseroid lies in the improvement of the numerical algorithm to calculate the triple or double integrals and the selection of the geometrical shape of the tesseroid mass body, e.g., the rotation method (Marotta and Barzaghi 2017; Marotta et al. 2019), splitting line method using the double exponential quadrature (Fukushima 2018a), different types of the regular, adaptive and combined subdivision (Li et al. 2011; Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Deng and Shen 2019; Lin and Denker 2019; Soler et al. 2019; Zhong et al. 2019; Zhao et al. 2019; Lin et al. 2020; Qiu and Chen 2020, 2021).

In addition, we study the influence of the latitude on gravitational effects up to the GC with the polynomial density up to fourth-order at the satellite height of $h=260$ km. The polar-singularity problem does not occur for the GC and GGT with different order polynomial density because of the applied Cartesian integral kernels of the tesseroid. The relative errors in $\log _{10}$ scale of gravitational effects up to the GC increase with the increased latitude. In other words, the geometrical shape of the tesseroid in the high latitude region, especially in the polar region, leads to an increase in the relative errors, whereas the relative errors in $\log _{10}$ scale are still within an acceptable range below $-3$. Under the assumption in Eq. (46), the density variation can be revealed in the superposition effects of the absolute errors of Laplace parameters of the GGT and GC in $\log _{10}$ scale with the influence of the height and latitude.

Regarding the potential applications of the formulae of the GC of a tesseroid in Cartesian integral kernels with arbitrary-order polynomial density in Eqs. (9–10), the atmospheric, topographic, and crustal effects of the Earth and other celestial bodies can be studied for the GC components in the gravity field modeling, which are similar to the GGT components (Eshagh 2009a, b, c, 2010, 2021). For example, the contribution of the binomial expansion up to degree four in topographic and atmospheric effects for the GC at the satellite altitude will be investigated in the future based on the similar application of the contribution of the second and third terms of the topographic and atmospheric effects for the GGT (Eshagh 2009a). In the future, the chosen exponents of the polynomial density coefficient of the GC will be examined for their topographic and atmospheric effects.

The analytical expressions for the gravitational effects up to the GC of a spherical shell with arbitrary-order polynomial density in Eqs. (19) and (25) can be regarded as the reference values for the tesseroid and other spherical mass bodies (e.g., spherical triangular tessellation (Zhang et al. 2018a)) in the numerical experiments. Other variable density models (e.g., exponential and sinusoidal density functions (Soler et al. 2019)) for the GC of the tesseroid and spherical shell will be focused on compared to the arbitrary order polynomial density model. Moreover, the residual topographic effects of the Earth can be investigated for the GC components using the spherical shell in the gravity field modeling, which are analogous to the GGT components (Kuhn and Hirt 2016). Note that the spherical harmonic expansion of the potential for the spherical shell even with irregular boundaries and laterally variable density was determined in the spectral domain (Eshagh 2010). The spherical harmonic coefficients of the potential of the irregular and heterogeneous layers (e.g., topographic and atmospheric effects in Eshagh (2009b); crustal effects in Eshagh (2021)) can simply be computed and inserted into the spherical harmonic expansions of the GC. Further investigations on the consistencies of the GC of the spherical shell between this paper in spatial domain and Eshagh (2009b, 2010, 2021) in spectral domain will be performed in the future, c.f. Kuhn and Seitz (2005), Hirt and Kuhn (2014), and Hirt et al. (2016).

When modeling the GC with an arbitrary-order polynomial density of the atmosphere, water, ice, topography, crust, mantle, and core of the Earth or other celestial bodies, the choice of density coefficient in the polynomial density in the practical situation should be made carefully according to the available density models (e.g., CRUST1.0 (Laske et al. 2013), GEMMA (Reguzzoni and Sampietro 2015), and UNB_TopoDens (Sheng et al. 2019)), seismic waves, and geological survey results. The mentioned density models include the density jumps at the boundaries of the mass bodies. The technique to treat the density jumps can be referred to Eqs. (26–27). In other words, the computation point can be slightly moved inside the mass bodies to avoid the density jumps based on the chosen double or quadruple precision. When adopting these density models in the application of the topographic effects, the density gradients can be taken, and the grid sizes of the tesseroids are $1^{\circ }\times 1^{\circ }$ for the CRUST1.0, $0.5^{\circ }\times 0.5^{\circ }$ for the GEMMA, and $30^{\prime \prime }\times 30^{\prime \prime }$ for the UNB_TopoDens.

The modeling of the GC of the tesseroid and spherical shell with different layers of the Earth or other celestial bodies belongs to the forward problem in geophysics. The low-order gravitational quantities (e.g., GV and GGT) of the tesseroid have been widely applied for the inversion in studies of the internal structures of the Earth or the Moon (Liang et al. 2014; Uieda and Barbosa 2017; Zhang et al. 2018b; Zhao et al. 2019, 2021). In the future, the inverse problem of the GC using different mass bodies (e.g., the tesseroid and spherical shell) that are likely to appear in applications will be investigated.

Appendix 1: Derivation of analytical expressions for the GP of a spherical shell with arbitrary-order polynomial density

The analytical expressions for the GP (V(r)) of a spherical shell with arbitrary-order polynomial density are derived with the computation point P located above (i.e., $r>r_2$) inside (i.e., $r_1\le r\le r_2$), and below (i.e., $r<r_1$) the spherical shell.

If the computation point P is located above the spherical shell (i.e., $r>r_2$), $\ell _1=r-r'$ and $\ell _2=r+r'$. Then, Eq. (15) can be presented as:

$$\begin{aligned} V(r)= & {} \frac{2\pi G}{r} \int \limits _{r'=r_1}^{r'=r_2} \int \limits _{\ell _1=r-r'}^{\ell _2=r+r'} \left( \sum _{n=0}^{N} \rho _n r'^{n+1}\right) \textrm{d} \ell \textrm{d} r' \nonumber \\= & {} \frac{4\pi G}{r} \int \limits _{r'=r_1}^{r'=r_2} \left( \sum _{n=0}^{N} \rho _n r'^{n+2}\right) \textrm{d} r' \nonumber \\= & {} 4\pi G \sum _{n=0}^{N} \rho _n \frac{r_2^{n+3}-r_1^{n+3}}{(n+3)r} \end{aligned}$$

(47)

When the computation point P is located below the spherical shell (i.e., $r<r_1$), $\ell _1=r'-r$ and $\ell _2=r'+r$. Under this condition, Eq. (15) can be derived as:

$$\begin{aligned} V(r)= & {} \frac{2\pi G}{r} \int \limits _{r'=r_1}^{r'=r_2} \int \limits _{\ell _1=r'-r}^{\ell _2=r'+r} \left( \sum _{n=0}^{N} \rho _n r'^{n+1}\right) \textrm{d} \ell \textrm{d} r' \nonumber \\= & {} 4\pi G \int \limits _{r'=r_1}^{r'=r_2} {\left( \sum _\mathrm{n=0}^{N} \rho _{n} r'^{{n}+1}\right) } \textrm{d} r' \nonumber \\= & {} 4\pi G \sum _{n=0}^{N}\rho _n \frac{r_2^{n+2}-r_1^{n+2}}{n+2} \end{aligned}$$

(48)

If the computation point P is located inside the spherical shell (i.e., $r_1 \le r \le r_2$), the original spherical shell can be divided as two spherical shell (Lin et al. 2020), i.e., the first spherical shell with inner and outer radii as $[r_1,r]$ where the computation point is above this spherical shell (i.e., $\ell _1=r-r'$ and $\ell _2=r+r'$) and the second spherical shell with inner and outer radii as $[r,r_2]$ where the computation point is below the spherical shell (i.e., $\ell _1=r'-r$ and $\ell _2=r'+r$). In this case, Eq. (15) can be derived as:

$$\begin{aligned} \begin{aligned} V(r)&= \frac{2\pi G}{r} \int \limits _{r'=r_1}^{r'=r} \int \limits _{\ell _1=r-r'}^{\ell _2=r+r'} \left( \sum _{n=0}^{N} \rho _n r'^{n+1}\right) \textrm{d} \ell \textrm{d} r' \\&\quad + \frac{2\pi G}{r} \int \limits _{r'=r}^{r'=r_2} \int _{\ell _1=r'-r}^{\ell _2=r'+r} \left( \sum _{n=0}^{N} \rho _n r'^{n+1}\right) \textrm{d} \ell \textrm{d} r' \\&= \frac{4\pi G}{r}\! \int \limits _{r'\!=\!r_1}^{r'\!=\!r} \!\left( \sum _{n=0}^{N} \!\rho _n r'^{n\!+\!2}\right) \!\textrm{d} r' \!+\! 4\pi G\! \int \limits _{r'=r}^{r'=r_2} \!\left( \sum _{n=0}^{N}\! \rho _n r'^{n+1}\right) \! \textrm{d} r' \\&= 4\pi G \sum _{n=0}^{N} \rho _n \bigg [\frac{r^{n+3}-r_1^{n+3}}{(n+3)r} + \frac{r_2^{n+2}-r^{n+2}}{n+2} \bigg ] \\&= 4\pi G \sum _{n=0}^{N} \rho _n \bigg [ \frac{r_2^{n+2}}{n+2} - \frac{r^{n+2}}{(n+2)(n+3)} - \frac{r_1^{n+3}}{(n+3)r} \bigg ] \end{aligned}\nonumber \\ \end{aligned}$$

(49)