Single-differenced models for GNSS-acoustic seafloor point positioning

Abstract

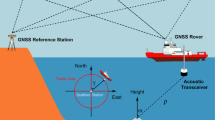
Seafloor transponder coordinates are determined by measurements between a ship-borne GNSS-acoustic transducer and the transponder. Differencing techniques can be applied to eliminate the impact of measurement biases for precise positioning effectively. The problem is that the correlations between differenced measurements must be adequately considered in the covariance matrix, which might cause a great number of calculations. This paper presents a set of conversion formulae to derive the differenced solution from the undifferenced model without nuisance parameters, and then we propose a dimension-reduction algorithm to fast solve the Gauss–Markov model augmented with nuisance parameters. The equivalence of the differenced and undifferenced solution is discussed within a wider range. It shows that: (1) the undifferenced solution can be converted into the differenced solution with only a few additional calculations; (2) there are a class of differencing schemes which are completely equivalent to each other having unique differencing equivalence weight (DEW) matrix; (3) the proposed algorithm is more efficient and has a good numerical stability relative to the blocking–stacking algorithm and the one-by-one elimination. The simulation and the real trial performed in a 3000-m depth sea area verified the proposed results.

Appendices

Appendix A: Eigenvalue decomposition of DEW matrix

According to the eigenvalue decomposition definition, the eigenpolynomial of $\widehat{{\mathbf{P}}}_{{\varepsilon_{L} }}$ reads (Seber 2008)

$$ \begin{gathered} p(\lambda ) = \det \left( {\widehat{P}_{{\varepsilon_{L} }} - \lambda {\mathbf{I}}} \right) \hfill \\ = \left| {\begin{array}{*{20}c} {(n - 1)/n - \lambda } & { - 1/n} & \cdots & { - 1/n} \\ { - 1/n} & {(n - 1)/n - \lambda } & \cdots & { - 1/n} \\ \vdots & \vdots & \ddots & \vdots \\ { - 1/n} & { - 1/n} & \cdots & {(n - 1)/n - \lambda } \\ \end{array} } \right|, \hfill \\ \end{gathered} $$

(A1)

where $\lambda$ is the eigenvalue. As the determinant is invariant to the elementary operation adding one row to the other row, respectively adding the nth, (n-1)th, …, 2nd rows to the first row of (A1), we have

$$ p(\lambda ) = - \lambda n\left| {\begin{array}{*{20}c} {1/n} & { - 1/n} & \cdots & { - 1/n} \\ {1/n} & {(n - 1)/n - \lambda } & \cdots & { - 1/n} \\ \vdots & \vdots & \ddots & \vdots \\ {1/n} & { - 1/n} & \cdots & {(n - 1)/n - \lambda } \\ \end{array} } \right|. $$

(A2)

In the same way, the first column multiple -1 and, respectively, adding it to the 2nd, 3rd and nth columns of (A2) results in

$$ p(\lambda ) = - \lambda n\left| {\begin{array}{*{20}c} {1/n} & 0 & \cdots & 0 \\ {1/n} & {1 - \lambda } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {1/n} & 0 & \cdots & {1 - \lambda } \\ \end{array} } \right| = - \lambda (1 - \lambda )^{n - 1} . $$

(A3)

Then, we can draw that there are a zero eigenvalue and n-1 multiple eigenvalues 1 s.

Next, we will deduce the eigenvectors of (A1) as follows:

(a) For the zero eigenvalue, the eigenvector is the nonzero solution of the following equation system:

$$ \left[ {\begin{array}{*{20}c} {(n - 1)/n} & { - 1/n} & \cdots & { - 1/n} \\ { - 1/n} & {(n - 1)/n} & \cdots & { - 1/n} \\ \vdots & \vdots & \ddots & { - 1/n} \\ { - 1/n} & { - 1/n} & \cdots & {(n - 1)/n} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right] = {\mathbf{0}}{\mathbf{.}} $$

(A4)

Similarly, with the above elementary operations, respectively, adding the nth, (n-1)th, …, 2nd equations to the first equation, Eq. (A4) becomes

$$ \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 \\ { - 1/n} & {(n - 1)/n} & \cdots & { - 1/n} \\ \vdots & \vdots & \ddots & { - 1/n} \\ { - 1/n} & { - 1/n} & \cdots & {(n - 1)/n} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right] = {\mathbf{0}}{\mathbf{.}} $$

(A5)

Further, respectively, subtracting the nth equation from the 2nd, 3rd and nth equations, we have

$$ \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & { - 1} \\ \vdots & \vdots & \ddots & \vdots & { - 1} \\ 0 & 0 & \cdots & 1 & { - 1} \\ { - 1/n} & { - 1/n} & \cdots & { - 1/n} & {(n - 1)/n} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ \begin{gathered} x_{2} \hfill \\ x_{3} \hfill \\ \end{gathered} \\ \vdots \\ {x_{n} } \\ \end{array} } \right] = {\mathbf{0,}} $$

(A6)

and then, we can write out the solution system of Eq. (A4) as

$$ \left[ {\begin{array}{*{20}c} {x_{1} } \\ \begin{gathered} x_{2} \hfill \\ x_{3} \hfill \\ \end{gathered} \\ \vdots \\ \begin{gathered} x_{n - 1} \hfill \\ x_{n} \hfill \\ \end{gathered} \\ \end{array} } \right] = k_{1} \left[ {\begin{array}{*{20}c} 1 \\ \begin{gathered} 1 \hfill \\ 1 \hfill \\ \end{gathered} \\ \vdots \\ \begin{gathered} 1 \hfill \\ 1 \hfill \\ \end{gathered} \\ \end{array} } \right] \quad k_{1} \in R, $$

(A7)

i.e., ${\mathbf{1}}_{n} = \left[ {1 \, 1 \, \cdots { 1}} \right]^{T}$ is the corresponding eigenvector, and its standard form reads

$$ {\mathbf{s}}_{n} = \left[ {n^{ - 1/2} \,\, n^{ - 1/2} \, \cdots \, n^{ - 1/2} } \right]^{T} . $$

(A8)

(b) For multiple eigenvalues 1 s, the eigenvectors are the nonzero solutions of the following equation system:

$$ \left[ {\begin{array}{*{20}c} { - 1/n} & { - 1/n} & \cdots & { - 1/n} \\ { - 1/n} & { - 1/n} & \cdots & { - 1/n} \\ \vdots & \vdots & \ddots & \vdots \\ { - 1/n} & { - 1/n} & \cdots & { - 1/n} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right] = {\mathbf{0}}{\mathbf{.}} $$

(A9)

Similarly, with the above deduction, respectively, subtracting the first equation from the nth, (n − 1)th, …, 2nd equations, we have

$$ \left[ {\begin{array}{*{20}c} { - 1/n} & { - 1/n} & \cdots & { - 1/n} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right] = {\rm 0,} $$

(A10)

then, we can write out the solution system of Eq. (A9) as

$$ \left[ {\begin{array}{*{20}c} {x_{1} } \\ \begin{gathered} x_{2} \hfill \\ x_{3} \hfill \\ \end{gathered} \\ \vdots \\ \begin{gathered} x_{n - 1} \hfill \\ x_{n} \hfill \\ \end{gathered} \\ \end{array} } \right] = k_{2} \left[ {\begin{array}{*{20}c} { - 1} \\ \begin{gathered} 1 \hfill \\ 0 \hfill \\ \end{gathered} \\ \vdots \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} } \right]{ + }k_{3} \left[ {\begin{array}{*{20}c} { - 1} \\ \begin{gathered} 0 \hfill \\ 1 \hfill \\ \end{gathered} \\ \vdots \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} } \right]{ + }...{ + }k_{n - 1} \left[ {\begin{array}{*{20}c} { - 1} \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ \vdots \\ \begin{gathered} 0 \hfill \\ 1 \hfill \\ \end{gathered} \\ \end{array} } \right] \, {\rm{where}}\, k_{2} ,k_{3} ,...,k_{n - 1} \in R, $$

(A11)

which can be used to define the n-1 eigenvectors.

Based on the above two cases (a) and (b), the eigenvectors can be given by the matrix

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} 1 & { - 1} & \cdots & { - 1} \\ 1 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & \cdots & 1 \\ \end{array} } \right], $$

(A12)

which can be orthogonalized to be the following form:

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} 1 & { - 1} & { - 1/2} & { - 1/3} & \cdots & { - 1/(n - 1)} \\ 1 & 1 & { - 1/2} & { - 1/3} & \cdots & { - 1/(n - 1)} \\ 1 & 0 & 1 & { - 1/3} & \cdots & { - 1/(n - 1)} \\ 1 & 0 & 0 & 1 & \cdots & { - 1/(n - 1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]. $$

(A13)

Moreover, we can obtain its standardization form as

$$ {\mathbf{R}}^{T} : = \left[ {\begin{array}{*{20}c} {\frac{1}{\sqrt n }} & { - \sqrt{\frac{1}{2}} } & { - \sqrt{\frac{1}{6}} } & { - \sqrt{\frac{1}{12}} } & \cdots & { - \sqrt {\frac{1}{n(n - 1)}} } \\ {\frac{1}{\sqrt n }} & {\sqrt{\frac{1}{2}} } & { - \sqrt{\frac{1}{6}} } & { - \sqrt{\frac{1}{12}} } & \cdots & { - \sqrt {\frac{1}{n(n - 1)}} } \\ {\frac{1}{\sqrt n }} & 0 & {2\sqrt{\frac{1}{6}} } & { - \sqrt{\frac{1}{12}} } & \cdots & { - \sqrt {\frac{1}{n(n - 1)}} } \\ {\frac{1}{\sqrt n }} & 0 & 0 & {3\sqrt{\frac{1}{12}} } & \cdots & { - \sqrt {\frac{1}{n(n - 1)}} } \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ {\frac{1}{\sqrt n }} & 0 & 0 & 0 & 0 & {(n - 1)\sqrt {\frac{1}{n(n - 1)}} } \\ \end{array} } \right]. $$

(A14)

Finally, we can give the eigenvalue decomposition of the DEW matrix as

$$ \widehat{{\mathbf{P}}}_{{\varepsilon_{L} }} = {\mathbf{R}}^{T} \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & \cdots & 1 \\ \end{array} } \right]{\mathbf{R,}} $$

(A15)

where the orthogonal matrix R is defined by 20, i.e.,

$$ {\mathbf{R}} = \left[ {\begin{array}{*{20}c} {\frac{1}{\sqrt n }} & {\frac{1}{\sqrt n }} & {\frac{1}{\sqrt n }} & {\frac{1}{\sqrt n }} & \cdots & {\frac{1}{\sqrt n }} \\ { - \sqrt{\frac{1}{2}} } & {\sqrt{\frac{1}{2}} } & 0 & 0 & \cdots & 0 \\ { - \sqrt{\frac{1}{6}} } & { - \sqrt{\frac{1}{6}} } & {2\sqrt{\frac{1}{6}} } & 0 & \cdots & 0 \\ { - \sqrt{\frac{1}{12}} } & { - \sqrt{\frac{1}{12}} } & { - \sqrt{\frac{1}{12}} } & {3\sqrt{\frac{1}{12}} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ { - \sqrt {\frac{1}{n(n - 1)}} } & { - \sqrt {\frac{1}{n(n - 1)}} } & { - \sqrt {\frac{1}{n(n - 1)}} } & { - \sqrt {\frac{1}{n(n - 1)}} } & \cdots & {(n - 1)\sqrt {\frac{1}{n(n - 1)}} } \\ \end{array} } \right]. $$

(A16)

Appendix B: Sequential LS adjustment for deleting observations

According to the recursive LS estimation (Koch 1999), we have

$$ \begin{gathered} {\hat{\mathbf{x}}} = ({\mathbf{N}}_{old} + {\mathbf{A}}_{new}^{T} {\mathbf{P}}_{new} {\mathbf{A}}_{new} )^{ - 1} ({\mathbf{A}}_{old}^{T} {\mathbf{P}}_{old} {\mathbf{L}}_{old} + {\mathbf{A}}_{new}^{T} {\mathbf{P}}_{new} {\mathbf{L}}_{new} ) \hfill \\ \, = {\hat{\mathbf{x}}}_{old} + {\varvec{Q}}_{{{\hat{\mathbf{x}}}_{old} }} {\mathbf{A}}_{new}^{T} ({\mathbf{P}}_{new}^{ - 1} + {\mathbf{A}}_{new} {\varvec{Q}}_{{{\hat{\mathbf{x}}}_{old} }} {\mathbf{A}}_{new}^{T} )^{ - 1} ({\mathbf{L}}_{new} - {\mathbf{A}}_{new} {\hat{\mathbf{x}}}_{old} ). \hfill \\ \end{gathered} $$

(A17)

The above formula illustrates the gain of the previous solution when adding new observations to the previous observation equation system. Once assuming ${\mathbf{P}}_{new}^{{}} = - {\mathbf{P}}_{del}^{{}}$, we can obtain the loss of the solution after removing some observations from the original observations, that

$$ {\hat{\mathbf{x}}} = {\hat{\mathbf{x}}}_{old} - {\mathbf{Ke}}_{del} , $$

(A18)

where

$$ {\mathbf{e}}_{del} : = ({\mathbf{L}}_{del} - {\mathbf{A}}_{del} {\hat{\mathbf{x}}}_{old} ) $$

(A19)

is the prediction error of the deleted observations relative to the previous solution,

$$ {\mathbf{K}}: = {\mathbf{Q}}_{{{\hat{\mathbf{x}}}_{old} }} {\mathbf{A}}_{del}^{T} {\mathbf{S}} $$

(A20)

is the loss information matrix,

$$ {\mathbf{S}}: = ({\mathbf{P}}_{del}^{ - 1} - {\mathbf{A}}_{del} {\mathbf{Q}}_{{{\hat{\mathbf{x}}}_{old} }} {\mathbf{A}}_{del}^{T} )^{ - 1} . $$

(A21)

${\mathbf{L}}_{del} ,{\mathbf{A}}_{del} ,{\mathbf{P}}_{del}^{{}}$ are, respectively, the deleted observations, and their corresponding design matrix and weight matrix.

In the same way, with the sequential LS adjustment principle, we can write out the loss information formula about the weighted sum of squared residuals, and it reads

$$ {\text{WSSR}} = {\text{WSSR}}_{{{\text{old}}}} - {\text{WSSR}}_{{{\text{del}}}} , $$

(A22)

where

$$ {\text{WRSS}}_{{{\text{del}}}} : = {\mathbf{e}}_{{{\text{del}}}}^{T} {\mathbf{Se}}_{{{\text{del}}}}^{{}} $$

(A23)

is the loss of the previous ${\text{WSSR}}_{{{\text{old}}}}$. Then, we can obtain the sequential formula about the unit weight variance as follows:

$$ \hat{\sigma }_{0}^{2} = \frac{{\hat{\sigma }_{{{\text{old}}}}^{2} t_{{{\text{old}}}} - {\text{WSSR}}_{{{\text{del}}}} }}{{t_{{{\text{old}}}} - n_{{{\text{del}}}} }}, $$

(A24)

where $\hat{\sigma }_{{{\text{old}}}}^{2}$ is the original estimation, $t_{{{\text{old}}}}$ is the previous freedom of observations, and $n_{{{\text{del}}}}$ is the number of deleted observations. In addition, the sequential formula about the co-factor matrix reads

$${\mathbf{Q}}_{{{\hat{\mathbf{x}}} }}: = ({\mathbf{I}} + {\mathbf{KA}}_{del} ){\mathbf{Q}}_{{{\hat{\mathbf{x}}}_{old} }}, $$

(A25)

where K is the loss information matrix defined by (A20). Combining (A24) with (A25), we have ${\mathbf{D}}_{{\hat{x}}} = {\mathbf{Q}}_{{\hat{x}}} \hat{\sigma }_{0}^{2}$.