A unifying model of strategic network formation

Abstract

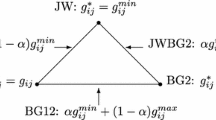
We provide a model that merges two basic models of strategic network formation and incorporates them as extreme cases: Jackson and Wolinsky’s connections model based on bilateral formation of links, and Bala and Goyal’s two-way flow model, where links can be unilaterally formed. In our model a link can be created unilaterally, but when it is only supported by one of the two players the flow through it suffers some friction or decay, but more than when it is supported by both players. When the friction in singly-supported links is maximal (i.e. there is no flow) we have Jackson and Wolinsky’s connections model, while when flow in singly-supported links is as good as in doubly-supported links we have Bala and Goyal’s two-way flow model. In this setting, a joint generalization of the results relative to efficiency and stability in both seminal papers is achieved, and the robustness in both models is tested with positive results.

Appendix

Lemma 1

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$ and $c>\max \{\delta -\delta ^{2},2\left( \alpha -\delta ^{2}\right) \}$, then the maximal value of a weak component containing m nodes and $m-1$ or more strong links is only reached by a star with $m-1$ strong links.

Proof

Let K be a weak component containing m nodes and $k_{s}\ge m-1$ strong links and $k_{w}\ge 0$ weak links. Without loss of generality, it can be assumed that no link is superfluous. Then,

$$\begin{aligned} v(K)=k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +p(\alpha ,\delta ), \end{aligned}$$

where $p(\alpha ,\delta )$ is a polynomial on $\alpha$ and $\delta$ with integer positive coefficients (summing up to $\max \{m\left( m-1\right) -2\left( k_{s}+k_{w}\right) ,0\}$, i.e. twice the number of pairs of nodes non-directly connected) multiplying monomials of the form $\alpha ^{q}\delta ^{r}$ with $q+r\ge 2$. As $\alpha \le \delta$, the maximal value of this polynomial is obtained when $p(\alpha ,\delta )=(m\left( m-1\right) -2\left( k_{s}+k_{w}\right) )\delta ^{2}$, that is

$$\begin{aligned} v(K)\le k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +\left( m\left( m-1\right) -2\left( k_{s}+k_{w}\right) \right) \delta ^{2}, \end{aligned}$$

while the value of a star of $m-1$ strong links with m nodes is

$$\begin{aligned} v(S_{m-1,0})=\left( m-1\right) \left( 2\delta -2c\right) +\left( m-1\right) \left( m-2\right) \delta ^{2}. \end{aligned}$$

Thus, the difference is

$$\begin{aligned} v(S_{m-1,0})-v(K)\ge \left( m-1-k_{s}\right) \left( 2\delta -2c-2\delta ^{2}\right) +k_{w}\left( 2\delta ^{2}-2\alpha +c\right) \ge 0, \end{aligned}$$

given that $m-1-k_{s}\le 0$, $2\delta -2c-2\delta ^{2}<0$ and $2\delta ^{2}-2\alpha +c>0$. Moreover, it is 0 only for $k_{s}=m-1$ and $k_{w}=0$. Finally, a component with $k_{s}=m-1$ and $k_{w}=0$ is necessarily minimally strongly connected, and the maximal value of a minimally strongly connected component is only reached by stars of strong links. $\square$

In what follows a mixed star consisting of $k_{s}$ strong links and $k_{w}$ weak links is denoted by $S_{k_{s},k_{w}}$.

Lemma 2

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$ and $c>2\alpha$, then a weak component containing m nodes and fewer than $m-1$ strong links is dominated by a mixed star with the same number of strong links.

Proof

Let K be a weak component containing m nodes and $k_{s}<m-1$ strong links and $k_{w}\ge m-1-k_{s}>0$ weak links. Without loss of generality, it can be assumed that no link is superfluous. Thus, reasoning as in the preceding lemma, we have:

$$\begin{aligned} v(K)\le k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +k_{s}\left( k_{s}-1\right) \delta ^{2} \\ +k_{s}\left( m-1-k_{s}\right) 2\alpha \delta +\left( m-1-k_{s}\right) \left( m-2-k_{s}\right) \alpha ^{2}, \end{aligned}$$

while the value of a star with $k_{s}$ strong links and $m-1-k_{s}$ weak links is

$$\begin{aligned} v\left( S_{k_{s},m-1-k_{s}}\right) =k_{s}\left( 2\delta -2c\right) +\left( m-1-k_{s}\right) \left( 2\alpha -c\right) \\ +k_{s}\left( k_{s}-1\right) \delta ^{2}+k_{s}\left( m-1-k_{s}\right) 2\alpha \delta +\left( m-1-k_{s}\right) \left( m-2-k_{s}\right) \alpha ^{2}. \end{aligned}$$

Thus, the difference is

$$\begin{aligned} v\left( S_{k_{s},m-1-k_{s}}\right) -v(K)=\left( c-2\alpha \right) \left( k_{s}+k_{w}-\left( m-1\right) \right) \ge 0, \end{aligned}$$

given that $k_{s}+k_{w}\ge m-1$ and $c>2\alpha$. And it is 0 only for $k_{s}+k_{w}=m-1$. Finally, the maximal value of a component with $m-1$ links is only reached by stars. $\square$

The next lemma establishes the same result for $2\left( \alpha -\alpha ^{2}\right)<c<2\alpha$.

Lemma 3

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$ and $2\left( \alpha -\alpha ^{2}\right)<c<2\alpha$, then a weak component containing m nodes and fewer than $m-1$ strong links is dominated by a mixed star with the same number of strong links.

Proof

Let K be a weak component containing m nodes, $k_{s}<m-1$ strong links and $k_{w}\ge m-1-k_{s}>0$ weak links. Without loss of generality, it can be assumed that no link is superfluous. The maximal value of the component here requires a more detailed discussion than in the case $c>2\alpha$ addressed in the preceding lemma. Thus we have

$$\begin{aligned} v(K)\le k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +A\delta ^{2}+B\alpha \delta +C\alpha ^{2}, \end{aligned}$$

where

$$\begin{aligned} A=\min \{k_{s}(k_{s}-1),m(m-1)-2k_{s}-2k_{w}\}. \end{aligned}$$

Two cases must be considered depending on which of these numbers is smaller:

1st case: $A=m(m-1)-2k_{s}-2k_{w}.$ In this case $B=C=0$, and we have

$$\begin{aligned} v(K)\le k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +(m(m-1)-2k_{s}-2k_{w})\delta ^{2}, \end{aligned}$$

while the value of a star with $k_{s}$ strong links and $m-1-k_{s}$ weak links is

$$\begin{aligned} v\left( S_{k_{s},m-1-k_{s}}\right)= & {} k_{s}\left( 2\delta -2c\right) +\left( m-1-k_{s}\right) \left( 2\alpha -c\right) \\&+k_{s}\left( k_{s}-1\right) \delta ^{2}+k_{s}\left( m-1-k_{s}\right) 2\alpha \delta \\&+\left( m-1-k_{s}\right) \left( m-2-k_{s}\right) \alpha ^{2}. \end{aligned}$$

Thus, the difference is

$$\begin{aligned}&v\left( S_{k_{s},m-1-k_{s}}\right) \\&\quad -v(K) \ge \left( m-1-k_{s}-k_{w}\right) \left( 2\alpha -c\right) \\&\quad +(k_{s}(k_{s}-1)-m(m-1)+2k_{s}+2k_{w})\delta ^{2} \\&\quad +k_{s}\left( m-1-k_{s}\right) 2\alpha \delta +\left( m-1-k_{s}\right) \left( m-2-k_{s}\right) \alpha ^{2} \\&=a\left( 2\alpha -c\right) +b\delta ^{2}+d\alpha \delta +e\alpha ^{2}, \end{aligned}$$

where a, b, d and e denote the coefficients in the last expression. Note that $a\le 0$, while b, d and e are $\ge 0$. As $2\alpha -c<2\alpha ^{2},$ by replacing $2\alpha -c$ by $2\alpha ^{2}$ in the last expression and taking into account that $\alpha \le \delta$ we have

$$\begin{aligned} v\left( S_{k_{s},m-1-k_{s}}\right) -v(K)\ge a2\alpha ^{2}+b\delta ^{2}+d\alpha \delta +e\alpha ^{2} \\ \ge a2\alpha ^{2}+b\alpha ^{2}+d\alpha ^{2}+e\alpha ^{2}=(2a+b+d+e)\alpha ^{2} \end{aligned}$$

Therefore, if $2a+b+d+e\ge 0$ the proof is concluded in the 1st case, and summing up these coefficients we have $2a+b+d+e=0.$

2nd case: $A=k_{s}(k_{s}-1).$ In this case $k_{s}(k_{s}-1)/2$ is the maximal number of non-directly linked pairs that can receive $\delta ^{2}$ from each other. Now

$$\begin{aligned} B=\min \{2k_{s}(m-1-k_{s}),m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1)\}. \end{aligned}$$

Thus, we again have two cases:

Case 2.1: $B=m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1).$ In this case $C=0$, and

$$\begin{aligned} v(K)\le & {} k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +k_{s}(k_{s}-1)\delta ^{2} \\&+(m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1))\alpha \delta . \end{aligned}$$

Thus, subtracting this value from that of a star with $k_{s}$ strong links and $m-1-k_{s}$ weak links the difference is

$$\begin{aligned}&v\left( S_{k_{s},m-1-k_{s}}\right) -v(K)\ge \left( m-1-k_{s}-k_{w}\right) \left( 2\alpha -c\right) \\&\quad +(2k_{s}(m-1-k_{s})-(m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1))\alpha \delta \\&\quad +\left( m-1-k_{s}\right) \left( m-2-k_{s}\right) \alpha ^{2}=a\left( 2\alpha -c\right) +b\alpha \delta +d\alpha ^{2}, \end{aligned}$$

and proceeding just as in the first case we similarly conclude that $v\left( S_{k_{s},m-1-k_{s}}\right) -v(K)\ge 0.$

Case 2.2: $B=2k_{s}(m-1-k_{s}).$ In this case

$$\begin{aligned} C=m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1)-2k_{s}(m-1-k_{s}),\text { and} \end{aligned}$$

$$\begin{aligned} v\left( S_{k_{s},m-1-k_{s}}\right) -v(K)\ge \left( m-1-k_{s}-k_{w}\right) \left( 2\alpha -c\right) \\ +(k_{s}+k_{w}-\left( m-1\right) )2\alpha ^{2}=a\left( 2\alpha -c\right) +b\alpha ^{2}, \end{aligned}$$

and proceeding again as before we conclude that $v\left( S_{k_{s},m-1-k_{s}}\right) -v(K)\ge 0.$ $\square$

Lemma 4

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$, and $c<2\left( \delta -\alpha \right)$, then: (i) in a non-empty efficient network all links are strong; (ii) if in addition $c>\delta -\delta ^{2}$, then a weak component is dominated by a star of strong links.

Proof

(i) Let g be a nonempty efficient network, and assume $ij\in g$ and $ji\notin g$, then the contribution of i’s (j’s) unit of value to j’s (i’s) payoff is $\alpha$, otherwise ij would be superfluous, but then, as $c<2\left( \delta -\alpha \right)$, by making ij double the sum of the payoffs of i and j would increase, and no other player’s payoff would decrease, which contradicts g’s efficiency.

(ii) Let K be a weak component with no superfluous links. By (i), all its links must be strong. But then by Lemma 1 it is dominated by a star of strong links (note that $c>2\left( \alpha -\delta ^{2}\right)$ follows easily from $c<2\left( \delta -\alpha \right)$ and $c>\delta -\delta ^{2}$, and Lemma 1 can be applied). $\square$

Lemmas 1, 2, 3 and 4 establish that, for different configurations of values of the parameters, any component is dominated by a star, possibly mixed. The following lemma shows that mixed stars are always dominated by stars containing only one type of link.

Lemma 5

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$, a star containing both strong and weak links is strictly dominated either by a star with the same number of links all of which are strong or by a star with the same number of links all of which are weak.

Proof

Let $S_{k_{s},k_{w}}$ be a star connecting m nodes with $k_{s}>0$ strong links and $k_{w}=m-1-k_{s}>0$ weak links. Its value is given by

$$\begin{aligned} v\left( S_{k_{s},k_{w}}\right) =k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +k_{s}\left( k_{s}-1\right) \delta ^{2}+2k_{s}k_{w}\alpha \delta +k_{w}\left( k_{w}-1\right) \alpha ^{2}. \end{aligned}$$

By making double a weak link, $S_{k_{s}+1,k_{w}-1}$ results, and

$$\begin{aligned} v\left( S_{k_{s}+1,k_{w}-1}\right)= & {} \left( k_{s}+1\right) \left( 2\delta -2c\right) +\left( k_{w}-1\right) \left( 2\alpha -c\right) \\&+\left( k_{s}+1\right) k_{s}\delta ^{2}+2\left( k_{s}+1\right) \left( k_{w}-1\right) \alpha \delta +\left( k_{w}-1\right) \left( k_{w}-2\right) \alpha ^{2}. \end{aligned}$$

Thus, as $k_{w}=m-1-k_{s}$, $v\left( S_{k_{s}+1,k_{w}-1}\right) -v\left( S_{k_{s},k_{w}}\right) =$

$$\begin{aligned} \left( 2\delta -2c\right) -\left( 2\alpha -c\right) +2\left( m-2\right) \alpha \left( \delta -\alpha \right) +2k_{s}\left( \delta -\alpha \right) ^{2}. \end{aligned}$$

(4)

Note that if this number is $>0$, the greater $k_{s}$ is the greater this number will be, and consequently the value of a star of strong links connecting m nodes is greater than that of $S_{k_{s},k_{w}}$.

By making a double link weak, $S_{k_{s}-1,k_{w}+1}$ results, and

$$\begin{aligned} v\left( S_{k_{s}-1,k_{w}+1}\right)= & {} \left( k_{s}-1\right) \left( 2\delta -2c\right) +\left( k_{w}+1\right) \left( 2\alpha -c\right) \\&+\left( k_{s}-1\right) \left( k_{s}-2\right) \delta ^{2}+2\left( k_{s}-1\right) \left( k_{w}+1\right) \alpha \delta +\left( k_{w}+1\right) k_{w}\alpha ^{2}. \end{aligned}$$

Thus, as $k_{w}=m-1-k_{s}$, $v\left( S_{k_{s}-1,k_{w}+1}\right) -v\left( S_{k_{s},k_{w}}\right) =$

$$\begin{aligned} -\left( 2\delta -2c\right) +\left( 2\alpha -c\right) +2\left( \delta ^{2}-m\alpha \delta +\left( m-1\right) \alpha ^{2}\right) -2k_{s}\left( \delta -\alpha \right) ^{2}. \end{aligned}$$

(5)

If this number is $>0$, the smaller $k_{s}$ is the greater this number will be and consequently the value of a star of weak links is greater than that of $S_{k_{s},k_{w}}$.

It only remains to show that the value necessarily increases by either making a weak link double or making a strong one weak, that is, either (4) or (5) is greater than 0. Write $X=\left( 2\delta -2c\right) -\left( 2\alpha -c\right)$, $Y=2\left( m-2\right) \alpha \left( \delta -\alpha \right) +2k_{s}\left( \delta -\alpha \right) ^{2}$ and $Y^{\prime }=2\left( \delta ^{2}-m\alpha \delta +\left( m-1\right) \alpha ^{2}\right) -2k_{s}\left( \delta -\alpha \right) ^{2}$. Thus we prove that necessarily either

$$\begin{aligned} v\left( S_{k_{s}+1,k_{w}-1}\right) -v\left( S_{k_{s},k_{w}}\right) =X+Y>0\quad \text {or}\quad V\left( S_{k_{s}-1,k_{w}+1}\right) -v\left( S_{k_{s},k_{w}}\right) =-X+Y^{\prime }>0. \end{aligned}$$

Assume $X+Y\le 0$, i.e. $X\le -Y$, then we prove that $-X+Y^{\prime }>0$, i.e. $X<Y^{\prime }$. For this it suffices to show that $-Y<Y^{\prime }$, i.e. $Y+Y^{\prime }>0.$ In fact we have $Y+Y^{\prime }=2\left( \delta -\alpha \right) ^{2}>0$. $\square$

Above $c=\delta -\delta ^{2}$ and $c=2\left( \alpha -\delta ^{2}\right)$ the preceding lemmas show the domination of stars, either of weak links or of strong links, for all the configurations of values of the parameters except the region considered in the next two lemmas, where two sorts of “hybrid” structure, somewhere between stars of strong links and weak-complete (see Fig. 12),¹⁸ serve as a term of comparison.

Fig. 12

“Hybrid” structures

Lemma 6

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$ and

$$\begin{aligned} \max \{2\left( \delta -\alpha \right) ,2\left( \alpha -\delta ^{2}\right) \}<c<2\left( \alpha -\alpha ^{2}\right) \text {,} \end{aligned}$$

then a weak component containing m nodes and fewer than $m-1$ strong links is dominated by a network consisting of a star with the same number of strong links and: (i) if $c>2\left( \alpha -\alpha \delta \right)$, with the rest of the nodes along with the center of the star forming a complete subnetwork of weak links; (ii) if $c<2\left( \alpha -\alpha \delta \right)$, any other pairs, except those of peripheral nodes of the star, are connected by weak links; (iii) in particular, in both cases, if the component contains no strong links it is dominated by the weak-complete graph.

Proof

(i):

Let K be a weak component, containing m nodes, $k_{s}<m-1$ strong links and $k_{w}\ge m-1-k_{s}>0$ weak links. Without loss of generality, it can be assumed that no link is superfluous. Thus we have

$$\begin{aligned} v(K)\le k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +A\delta ^{2}+B\alpha \delta , \end{aligned}$$

where

$$\begin{aligned} A=\min \{k_{s}(k_{s}-1),m(m-1)-2k_{s}-2k_{w}\}. \end{aligned}$$

Let $g_{k_{s}}^{*}$ be a m-node network consisting of a star with $k_{s}$ strong links and the rest of the nodes along with the center of the star forming a complete subnetwork of weak links (see Fig. 12a). Then

$$\begin{aligned} v(g_{k_{s}}^{*})=k_{s}\left( 2\delta -2c\right) +k_{w}^{\prime }\left( 2\alpha -c\right) +A^{\prime }\delta ^{2}+B^{\prime }\alpha \delta , \end{aligned}$$

(6)

where

$$\begin{aligned} k_{w}^{\prime }=(m-k_{s})(m-k_{s}-1)/2\text {,\quad }A^{\prime }=k_{s}(k_{s}-1)\text {\quad and\quad }B^{\prime }=2k_{s}(m-k_{s}-1). \end{aligned}$$

(7)

Now, depending on the value of A, we have two cases: 1st case: $A=m(m-1)-2k_{s}-2k_{w}.$ In this case $B=0$ and $A\le A^{\prime }$. Then we have

$$\begin{aligned} v(g_{k_{s}}^{*})-v(K)\ge (k_{w}^{\prime }-k_{w})\left( 2\alpha -c\right) +(A^{\prime }-A)\delta ^{2}+B^{\prime }\alpha \delta . \end{aligned}$$

As $k_{w}^{\prime }+A^{\prime }/2+B^{\prime }/2=k_{w}+A/2$ and $A\le A^{\prime }$, $k_{w}^{\prime }\le k_{w}$. And as $2\alpha -c<2\alpha \delta$ and $k_{w}^{\prime }-k_{w}+B^{\prime }/2=A/2-A^{\prime }/2$, and $2\alpha \delta <2\delta ^{2}$ we have:

$$\begin{aligned} v(g_{k_{s}}^{*})-v(K)\ge (A^{\prime }-A)\delta ^{2}+(k_{w}^{\prime }-k_{w}+B^{\prime }/2)2\alpha \delta \\ \ge (k_{w}^{\prime }-k_{w}+B^{\prime }/2+A^{\prime }/2-A/2)2\alpha \delta =0. \end{aligned}$$

2nd case: $A=k_{s}(k_{s}-1).$ Then

$$\begin{aligned} B=\min \{2k_{s}(m-1-k_{s}),m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1)\}. \end{aligned}$$

In both cases $B^{\prime }\ge B\ge 0$, and $k_{w}\ge k_{w}^{\prime }\ge 0$, with $k_{w}^{\prime }+B^{\prime }/2=k_{w}+B/2$. And as $c<2\left( \alpha -\alpha \delta \right)$, we have

$$\begin{aligned} v(g_{k_{s}}^{*})-v(K)\ge & {} (k_{w}^{\prime }-k_{w})\left( 2\alpha -c\right) +(B^{\prime }-B)2\alpha \delta \\\ge & {} (k_{w}^{\prime }-k_{w})(2\alpha -c-2\alpha \delta )\ge 0. \end{aligned}$$

(ii):

Let K be a weak component as in (i). Let $g_{k_{s}}^{**}$ be a m-node network consisting of a star with $k_{s}$ strong links and any other pairs of nodes, except those of peripheral nodes of the star, connected by weak links (see Fig. 12b). Thus

$$\begin{aligned} v(g_{k_{s}}^{**})=k_{s}\left( 2\delta -2c\right) +k_{w}^{\prime }\left( 2\alpha -c\right) +A^{\prime }\delta ^{2}, \end{aligned}$$

(8)

where

$$\begin{aligned} A^{\prime }=k_{s}(k_{s}-1)\text {\quad and\quad }k_{w}^{\prime }=m(m-1)/2-k_{s}-k_{s}(k_{s}-1)/2. \end{aligned}$$

(9)

Two cases must be considered depending on the value of A: 1st case: $A=m(m-1)-2k_{s}-2k_{w}.$ In this case $B=0$ and $A\le A^{\prime }$. Thus we have

$$\begin{aligned} v(K)\le k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +A\delta ^{2}, \end{aligned}$$

and consequently

$$\begin{aligned} v(g_{k_{s}}^{**})-v(K)\ge (k_{w}^{\prime }-k_{w})\left( 2\alpha -c\right) +(A^{\prime }-A)\delta ^{2}. \end{aligned}$$

As $k_{w}^{\prime }+A^{\prime }/2=k_{w}+A/2$, that is, $k_{w}^{\prime }-k_{w}=A/2-A^{\prime }/2\le 0$, and we have

$$\begin{aligned} v(g_{k_{s}}^{**})-v(K)\ge (k_{w}^{\prime }-k_{w})(2\alpha -c-2\delta ^{2})\ge 0. \end{aligned}$$

2nd case: $A=k_{s}(k_{s}-1).$ Thus

$$\begin{aligned} B=\min \{2k_{s}(m-1-k_{s}),m(m-1)-2k_{s}-2k_{w}-k_{s}(k_{s}-1)\}. \end{aligned}$$

In this case $B\ge 0$, and as $k_{w}+B/2=k_{w}^{\prime }$ and $c<2\left( \alpha -\alpha \delta \right)$, i.e. $2\alpha \delta <2\alpha -c$, we have:

$$\begin{aligned} v(K)\le & {} k_{s}\left( 2\delta -2c\right) +k_{w}\left( 2\alpha -c\right) +k_{s}(k_{s}-1)\delta ^{2}+B\alpha \delta \\\le & {} k_{s}\left( 2\delta -2c\right) +(k_{w}+B/2)\left( 2\alpha -c\right) +k_{s}(k_{s}-1)\delta ^{2}. \end{aligned}$$

Thus

$$\begin{aligned} v(g_{k_{s}}^{**})-v(K)\ge (k_{w}^{\prime }-(k_{w}+B/2))(2\alpha -c)=0. \end{aligned}$$

(iii):

Just note that in both cases, (i) and (ii), the component is assumed to have fewer than $m-1$ strong links, which includes the case of no strong links. But note that the structure proved to dominate the component, i.e. $g_{0}^{*}$ or $g_{0}^{**}$, is then a weak-complete network. $\square$

Lemma 7

If the payoff function is given by (3) with $0\le \alpha \le \delta <1$ and

$$\begin{aligned} \max \{2\left( \delta -\alpha \right) ,2\left( \alpha -\delta ^{2}\right) \}<c<2\left( \alpha -\alpha ^{2}\right) \text {,} \end{aligned}$$

then a weak component of a network is dominated either by a weak-complete subnetwork or by a star of strong links with the same number of nodes.

Proof

In view of the preceding lemma, in this region a component with no strong links is dominated by a weak-complete network with the same number of nodes. If a component with m nodes contains at least $m-1$ strong links, Lemma 1 establishes that it is dominated by a star with $m-1$ strong links. If it contains some strong links, but fewer than $m-1$, Lemma 6 shows that it is dominated by one of two types of structure with the same number $k_{s}$ of strong links, either $g_{k_{s}}^{*}$ or $g_{k_{s}}^{**}$. We now prove that such structures are dominated either by a weak-complete subnetwork or by star of strong links with the same number of nodes. Consider first the case when $c>2\left( \alpha -\alpha \delta \right)$. In this case, the dominant structure is $g_{k_{s}}^{*}$. Thus $v(g_{k_{s}}^{*})$ is given by (6), with (7). Thus, comparing this value with that of $v(g_{k_{s}+1}^{*})$ and $v(g_{k_{s}-1}^{*})$, we have

$$\begin{aligned} v(g_{k_{s}+1}^{*})-v(g_{k_{s}}^{*})= & {} X+\left( 2\alpha -c\right) -4\alpha \delta , \\ v(g_{k_{s}-1}^{*})-v(g_{k_{s}}^{*})= & {} -X+2\delta ^{2}, \end{aligned}$$

where $X=2\delta -2c-(m-k_{s})\left( 2\alpha -c\right) +k_{s}2\delta ^{2}+(m-2k_{s})2\alpha \delta .$ We prove that one of these differences is necessarily positive. Assume $-X+2\delta ^{2}\le 0,$ that is, $X\ge 2\delta ^{2}.$ Thus

$$\begin{aligned} v(g_{k_{s}+1}^{*})-v(g_{k_{s}}^{*})\ge 2\delta ^{2}+2\alpha -c-4\alpha \delta , \end{aligned}$$

which is $>0$ if $c<2\delta ^{2}+2\alpha -4\alpha \delta$. To see that this is so, note that $\alpha <\delta$, thus $(\alpha -\delta )^{2}>0$, i.e. $\alpha ^{2}+\delta ^{2}-2\alpha \delta >0.$ Then, as $c<2\alpha -2\alpha ^{2}$

$$\begin{aligned} c<2\alpha -2\alpha ^{2}<2\alpha -2(2\alpha \delta -\delta ^{2})<2\delta ^{2}+2\alpha -4\alpha \delta . \end{aligned}$$

Therefore one of the two differences must be positive. In other words $g_{k_{s}}^{*}$ is dominated either by $g_{k_{s}-1}^{*}$ or by $g_{k_{s}+1}^{*}$. This entails that $g_{k_{s}}^{*}$ is dominated by one of the extreme cases: $g_{0}^{*}$ or $g_{m}^{*}$, i.e. a m -node weak-complete network or star of strong links. $\square$

Proof of Proposition 1:

(i):

As $c<\delta$, an efficient network is non-empty, and, as $c<2\left( \delta -\alpha \right)$, by Lemma 4(i), in a non-empty efficient network all links are strong. Let g then be a network where all links are strong and assume nodes i and j are not connected. As $c<\delta -\delta ^{2}$, i.e. $\delta ^{2}<\delta -c$, both i and j improve their payoffs if the strong link $\overline{ij}$ forms, and the other players’ payoffs do not decrease. Therefore, the unique efficient network is the strong-complete one.

(ii):

Consider first the subregion where $c<2\left( \alpha -\delta ^{2}\right)$. Let g be a network where two nodes, i and j, are not directly connected. Thus i $\left( j\right)$ receives at most $\delta ^{2}$ from j’s $\left( i\text {'s}\right)$ unit of value. As $2\delta ^{2}<2\alpha -c$, the sum of the payoffs of i and j increases if a weak link between them forms, and the other players’ payoffs do not decrease. Thus, if $c<2\left( \alpha -\delta ^{2}\right)$ an efficient network must be complete. Note that $\alpha$ must be greater than $\delta ^{2}$. Now as $2\left( \delta -\alpha \right) <c$, if a strong link $\overline{ij}$ in a complete network is replaced by a weak link, then the sum of the payoffs of i and j increases, and the other players’ payoffs do not decrease. Therefore, if $2\left( \delta -\alpha \right)<c<2\left( \alpha -\delta ^{2}\right)$ then the unique efficient profile is the weak-complete graph. The rest of the region remains to be examined, i.e. where $c\ge 2\left( \alpha -\delta ^{2}\right)$. But this is a subset of the range of values of the parameters considered in Lemmas 6 and 7, where any component is dominated either by a weak-complete subnetwork or by a star of strong links with the same number of nodes. As $c<2\left( \alpha -\alpha ^{2}\right) <2\alpha$, an efficient network must be connected, therefore any network is dominated either by a weak-complete network or by an all-encompassing star of strong links. Finally, it can be checked immediately that the former dominates the latter if and only if $c\left( n-4\right) \le 2n\alpha -4\delta -2\left( n-2\right) \delta ^{2}$, strictly if the inequality is strict, while both structures are equally efficient in case of equality.

(iii):

By Lemma 1, any component with at least $m-1$ strong links is dominated by a star of strong links. It remains to be checked that this is also the case if it has fewer than $m-1$ strong links. As seen in Lemma 4, in this region, when $c<2\left( \delta -\alpha \right)$, a weak component is dominated by a star of strong links, therefore the statement is proven in this case. Now consider the case $c\ge 2\left( \delta -\alpha \right)$. If $c>2\alpha$, Lemma 2 ensures that any component is dominated by a mixed star with the same number of strong links, and by Lemma 3 the same holds if $2\left( \alpha -\alpha ^{2}\right)<c<2\alpha .$ By Lemma 5 mixed stars are dominated either by stars of weak links or by stars of strong links, so this conclusion applies to the subset of the region under consideration where $c>2\left( \alpha -\alpha ^{2}\right)$. The subset where $2\left( \delta -\alpha \right) \le c<2\left( \alpha -\alpha ^{2}\right)$ remains to be discussed, where Lemmas 6 and 7 apply and ensure that any component is dominated either by a weak-complete subnetwork or by a star of strong links with the same number of nodes. If $c<2\alpha$, an efficient network must be connected, therefore in this region any network is dominated either by a weak-complete network or by an all-encompassing star of strong links. But the latter is dominated by the former if and only if $c\left( n-4\right) \le 2n\alpha -4\delta -2\left( n-2\right) \delta ^{2}$, strictly if the inequality is strict, while both structures are equally efficient in case of equality. Now if $c\ge 2\alpha$, Lemmas 2 and 5, ensure that any component of an efficient network must be a star of either weak links or strong links. As the value of a component of an efficient network must be non-negative, it is immediate to check that the value of a star with $m_{1}+m_{2}$ nodes is greater than the sum of the values of two stars with $m_{1}$ and $m_{2}$ nodes each. In short, it is proved that throughout the region a component is dominated by a star of strong or of weak links. It then follows immediately that the former dominates the latter if and only if $c\le 2\left( \delta -\alpha \right) +\left( n-2\right) \left( \delta ^{2}-\alpha ^{2}\right)$, strictly if the inequality is strict, while both structures are equally efficient in case of equality. Thus, in the whole region the only non-empty efficient network is the all-encompassing star of strong links. Finally, the all-encompassing star of strong links yields a non-negative value if and only if $c<\delta +\left( n-2\right) \delta ^{2}/2$.

(iv):

By the same argument used in $\left( iii\right)$, Lemmas 1–5 ensure that in this region any network is dominated by an all-encompassing star of weak links or by one of strong links. As stated before, the former dominates the latter if and only if $c\ge 2\left( \delta -\alpha \right) +\left( n-2\right) \left( \delta ^{2}-\alpha ^{2}\right)$, strictly if the inequality is strict, while both structures are equally efficient in case of equality. Thus, in the whole region the only efficient non-empty network is the all-encompassing star of weak links. Finally, the all-encompassing star of weak links yields non-negative value if and only if $c<2\alpha +\left( n-2\right) \alpha ^{2}$.

(v):

This follows from the discussion in $\left( iii\right)$ and $\left( iv\right)$. $\square$

Proof of Proposition 2:

• (i) Let g be a Nash network. Assume g has more than one non-trivial weak component. If any of them is not strongly connected it contains at least one weak link, say ij, i.e. $ij\in g$ and $ji\notin g$, but then any node in a different weak component will benefit by creating a weak link with j, which contradicts that g is a Nash network.

• (ii) Let g be the strong-complete network. A player i has no incentive to withdraw support for a double link $\overline{ij}$ (or a set of them), if and only if $\delta -c$ is greater than or equal to $\alpha$ and to $\delta ^{2}$. In other words, if $\delta -c\ge \max \{\alpha ,\delta ^{2}\}$, which is equivalent to $c\le \min \{\delta -\delta ^{2},\delta -\alpha \}$. Now assume these conditions hold strictly, then the network described is strict Nash.

• (iii) Let g be a weak-complete network. For a weak link $ij\in g$, player i has no incentive to withdraw support for it if and only if $\alpha -c\ge \alpha ^{2}$. On the other hand, j has no incentive to double this link if and only if $\alpha \ge \delta -c$. Thus we have two necessary conditions for pairwise Nash stability: $\delta -\alpha \le c\le \alpha -\alpha ^{2}$. Finally, i has no incentive to switch its support from ij to another, say ik, thus making double the existing weak link ki, if and only if $2\alpha \ge \delta +\alpha \delta ,$ i.e. $\delta \le 2\alpha /\left( 1+\alpha \right) .$ Now assume all these conditions hold strictly. Then, as $c<\alpha -\alpha ^{2}<\alpha ,$ either of the two players in any pair not connected by a link would benefit by creating a weak link. Thus g must be complete, and as $c>\delta -\alpha$ no strong link can exist. Therefore g is weak-complete. Thus, if all these conditions hold (strictly) g is a Nash (strict Nash) network.

• (iv) Let g be an all-encompassing star of strong links. The center has no incentive to withdraw support for a link (or a set of them) if $\delta -c\ge \alpha$. No peripheral node is interested in forming a weak link with another (or a set of them) if $c\ge \alpha -\delta ^{2}$. If these conditions hold strictly, then g is strict Nash.

• (v) Let g be an all-encompassing periphery-sponsored star. No peripheral node has an incentive to sever its link if $\alpha +(n-2)\alpha ^{2}-c\ge 0$ . If $c\ge \delta -\alpha$, the center has no incentive to double a link (or a set of them). If $c\ge \alpha -\alpha ^{2}$ no peripheral node has an incentive to form a weak link with another (or a set of them). Therefore, if all three conditions hold (strictly) g is a Nash (strict Nash) network. In (vi) we show that for other stars to be Nash $c\le \alpha$ is required.

• (vi) Let g be an all-encompassing star. If it is center-sponsored or a mixed-sponsored star, the center has no incentive to sever a link (or a set of them) if $c\le \alpha$ (which does not apply if the star is periphery-sponsored) and no peripheral node whose link is supported by the center has an incentive to double it if $\alpha +(n-2)\alpha ^{2}\ge \delta +(n-2)\delta \alpha -c$, i.e. if $c\ge (\delta -\alpha )(1+(n-2)\alpha )$. Finally, no peripheral node is interested in forming a weak link with another (or a set of them) if $c\ge \alpha -\alpha ^{2}$. If these conditions hold strictly, then g is strict Nash.

• (vii) This is straightforward. $\square$

Proof of Proposition 3:

• (i) Let g be a pairwise Nash stable network. Assume g has more than one non-trivial weak component. Let $ij\in g$ and $kl\in g$ be two links in different weak components. If both are strong, i.e. $\overline{ij}\in g$ and $\overline{kl}\in g$, it easily follows that both j and k benefit by creating a strong link $\overline{jk}$. If $\alpha >0$ and one of them, say ij, is weak, i.e. $ji\notin g$, then k will benefit by creating a weak link with j. In both cases there is a contradiction with pairwise stability.

• (ii) By Proposition 2(ii), the strong-complete network is strict Nash under these conditions. Now assume this condition holds strictly: any two players not connected by a link must then benefit by forming a strong link, and any player benefits by making a weak link supported by another player double, so only the strong-complete network is pairwise Nash stable.

• (iii) By Proposition 2(iii), under these conditions a weak-complete network is a Nash network. Now assume all these conditions hold strictly. Then, as $c<\alpha -\alpha ^{2}<\alpha ,$ either of the two players in any pair not connected by a link would benefit by creating a weak link. Thus g must be complete, and as $c>\delta -\alpha$ no strong link can exist. Therefore g is weak-complete. Finally, $\delta <2\alpha /\left( 1+\alpha \right)$ guarantees that weak-complete networks alone are pairwise Nash stable. Note that, as it occurs with the strong-complete, pairwise coordination does not provide actual new options.

• (iv) By Proposition 2(iv), under these conditions an all-encompassing star of strong links is a Nash network. In such a star no two peripheral nodes are interested in forming a strong link if $c\ge \delta -\delta ^{2}$, which is stronger than $c\ge \alpha -\delta ^{2}$ and consequently pairwise Nash stability strictly refines Nash stability for these structures.

• (v) By Proposition 2(v), under these conditions an all-encompassing periphery-sponsored star is a Nash network. And no pair of peripheral nodes are interested in forming a strong link if $\alpha +(n-2)\alpha ^{2}-c\ge \delta +\alpha +(n-3)\alpha ^{2}-2c\ge 0$, that is, if $c\ge \delta -\alpha ^{2}$. Therefore, g is pairwise Nash stable if and only if $\delta -\alpha ^{2}\le c\le \alpha +(n-2)\alpha ^{2}$.

• (vi) By Proposition 2(vi), under these conditions an all-encompassing star of weak links is a Nash network. Note that $\delta -\alpha ^{2}\le c\le \alpha$ implies $\delta -\alpha ^{2}\le c\le \alpha +(n-2)\alpha ^{2}$, therefore, as proven in (v), an all-encompassing periphery-sponsored star is pairwise Nash stable. Now let g be an all-encompassing center-sponsored or mixed-sponsored star of weak links. Then, no pair of peripheral nodes are interested in forming a strong link (in this respect the situation is entirely similar to (v)) if $c\ge \delta -\alpha ^{2}$.

• (vii) This is straightforward. $\square$

Proof of Corollary 1:

Assume g is a pairwise Nash stable network. By Proposition 2(i), g is weakly connected. If $\delta -\alpha <c$, no peripheral player can be connected by a strong link, nor sponsored by a weak link if $\alpha <c$. Therefore a peripheral node can only be connected by a weak link supported by itself. But only one such peripheral node can exist, because if there were more, as $c<\delta -\alpha ^{2}$, it would then be profitable for any pair of them to form a strong link. Consequently, under these conditions g cannot be a weakly connected graph with no cycles. $\square$