Sample selection models for count data in R

Abstract

We provide a detailed hands-on tutorial for the R package SemiParSampleSel (version 1.5). The package implements selection models for count responses fitted by penalized maximum likelihood estimation. The approach can deal with non-random sample selection, flexible covariate effects, heterogeneous selection mechanisms and varying distributional parameters. We provide an overview of the theoretical background and then demonstrate how SemiParSampleSel can be used to fit interpretable models of different complexity. We use data from the German Socio-Economic Panel survey (SOEP v28, 2012. doi:10.5684/soep.v28) throughout the tutorial.

1 Introduction

The sample selection model was introduced by Gronau (1974), Lewis (1974) and Heckman (1976) to deal with the situation in which the observations available for statistical analysis are not from a random sample of the population, and discussed by Heckman (1990) among others. This issue occurs when individuals select themselves into (or out of) the sample based on a combination of observed and unobserved characteristics. Estimates based on models that ignore such a non-random selection may be biased and inconsistent. This situation can be rectified using sample selection models, which typically consist of a two-equation system: a binary selection equation determining whether a particular statistical unit will be available in the outcome equation.

Let us consider a case study which uses data from the German Socio-Economic Panel survey (SOEP v28 2012) which will be analyzed in more detail in Sect. 3. The aim of the study is to estimate the determinants of labor mobility as well as the average number of job changes. Non-random selection arises if the sample consisting of individuals who are in the job market differ in important characteristics from the sample of individuals who are not part of the market. If the link between the decision to be part of the market and number of direct job changes (i.e., changes without an intervening spell of unemployment) is through observables, then selection bias can be avoided by accounting for these variables. However, if the link is also through unobservables then inconsistent parameter estimates are produced when using classic univariate modeling approaches. There are several other aspects that may complicate modeling labor mobility. Variables such as employment and length of education in years may have non-linear impacts on decision of being part of the job market and on the number of direct job changes, possibly due to productivity and life-cycle effects; imposing a priori a linear relationship (or non-linear by simply using quadratic polynomials, for example) could mean failing to capture interesting complex relationships. In addition, the assumption of bivariate normality employed in many sample selection models between, in this case, decision to be part of the job market and number of job changes may be too restrictive for applied work and it is typically made for mathematical convenience. Finally, the outcome of interest is a count variable.

The literature on sample selection models is vast and many variants of such models have been proposed; without claim of exhaustiveness here we mention some works. Chib et al. (2009) and Wiesenfarth and Kneib (2010) introduced two estimation methods to deal with non-linear covariate effects. Specifically, the approach of the former authors is based on Markov chain Monte Carlo simulation techniques and uses a simultaneous equation system that incorporates Bayesian versions of penalized smoothing splines. The latter further extended this approach by introducing a Bayesian algorithm based on low rank penalized B-splines for non-linear and varying-coefficient effects and Markov random-field priors for spatial effects. Marra and Radice (2013) proposed a frequentist counterpart which is computationally fast. Greene (1997), Terza (1998), Winkelmann (1998), Miranda (2004), Miranda and Rabe-Hesketh (2006) and Bratti and Miranda (2011) discuss fully parametric methods for estimating count data models allowing for overdispersion. These are based on the Poisson distribution and normally distributed unobserved heterogeneity. The common and limiting factor of these approaches is the assumption of bivariate normality.

Various methods that relax the assumption of normality have been proposed over the years; these include semiparametric (e.g., Gallant and Nychka 1987; Lee 1994; Powell 1994; Newey 2009) and nonparametric methods (e.g., Das et al. 2003; Lee 2008; Chen and Zhou 2010). Another way to relax the normality assumption is to use non-Gaussian parametric distributions. Recently, Marchenko and Genton (2012) and Ding (2014) extended the sample selection model to deal with heavy-tailedness by using the bivariate Student-t distribution. Another example of non-Gaussian parametric approach is copula modeling which allows for a great deal of flexibility in specifying the joint and marginal distributions of the selection and outcome equations (e.g., Smith 2003; Prieger 2002; Hasebe and Vijverberg 2012; Schwiebert 2013). In the context of count responses, Marra and Wyszynski (2016) propose a copula-based approach, where covariates can be modeled flexibly using splines. There are advantages and disadvantages to both approaches (semi/non-parametric and parametric). The strongest point of the semi/non-parametric approach is the property of maintaining consistency of such estimators even disposing, in part or altogether, of distributional assumptions. However, semi/non-parametric methods are usually restricted when it comes to including a large set of covariates in the model and the resulting estimates are inefficient relatively to fully parametrized models (e.g., Bhat and Eluru 2009). To date, packages implementing semi/non-parametric procedures are CPU-intensive and the set of options provided is often quite limited. As for the parametric approach, many scholars agree upon its greater computational feasibility as compared to semi/non-parametric approaches, which allows for the use of familiar tools such as maximum likelihood without requiring simulation methods or numerical integration. As pointed out by Smith (2003), maximum likelihood techniques allow for the simultaneous estimation of all model parameters, and such methods, if the usual regularity conditions hold and the model is correctly specified, ensure consistent, efficient and asymptotically normal estimators. While a fully parametric copula approach is less flexible than semi/non-parametric approaches, it is still allows the user to assess the sensitivity of results to different modeling assumptions. Specifically, the wide selection of potential copulae allows the modeler to perform sensitivity analysis to assess changes in results.

Some of the methods described above are implemented in popular software packages like SAS (SAS Institute Inc 2013), Stata (StataCorp 2011), LIMDEP (Greene 2007), EViews (IHS Global Inc. 2015) and R (R Development Core Team 2016). For example, the conventional Heckman sample selection model can be fitted in SAS using the proc qlim procedure and in Stata using heckman statement. The non-parametric method by Lee (2008) can be employed using the Stata package leebounds and the bivariate Student-t distribution Heckman model using heckt. The Poisson count data model by Miranda and Rabe-Hesketh (2006) can be employed in Stata using ssm. In R the sample selection packages are sampleSelection (Toomet and Henningsen 2008), bayesSampleSelection (Wiesenfarth and Kneib 2010), ssmrob (Zhelonkin et al. 2013) and SemiParBIVProbit (Marra and Radice 2015). sampleSelection and bayesSampleSelection make the assumption of bivariate normality between the model equations. sampleSelection and ssmrob assume a priori that continuous regressors have linear or pre-specified non-linear relationships to the responses, whereas ssmrob relaxes the assumption of bivariate normality by providing a robust two-stage estimator of Heckman’s approach. sampleSelection and SemiParBIVProbit support binary responses for the outcome equation, with the latter allowing for non-linear covariate effects and non-Gaussian bivariate distributions. The R package SemiParSampleSel (Marra et al. 2017b; Wojtyś et al. 2016) deals simultaneously with non-random sample selection, non-linear covariate effects and non-normal bivariate distribution between the model equations. Covariate-response relationships are flexibly modeled using a spline approach, whereas non-normal distributions are dealt with by using copula functions. Note that copulaSampleSel() in GJRM (Marra and Radice 2017) works as SemiParSampleSel() in SemiParSampleSel.

In this paper, we further extend the SemiParSampleSel package (v. 1.5) by allowing the outcome to be modeled as a discrete random variable, and by allowing the mean, the higher order moments and the copula dependence parameter to be heterogeneous by specifying flexible linear predictor equations for each of them. Our approach of allowing multiple parameters to vary by observation follows the same rationale provided by Rigby and Stasinopoulos (2005), who extended generalized additive models to the context of more complex response distributions. As suggested by Marra and Wyszynski (2016), we expand the number of available outcome distributions; these include, for instance, beta binomial and zero inflated margins (see “Appendix 1”).

The rest of the paper is organized as follows: in Sect. 2, we provide a brief theoretical overview of the sample selection modeling approach for count data and its properties (this is based on: Marra and Wyszynski 2016). Section 3 presents SemiParSampleSel by describing its main infrastructure and how to use the package to obtain interpretable statistical models. Using SemiParSampleSel, we provide a step-by-step illustration on how to use sample selection models for count data in R to build a prediction model for SOEP data. A summary of the paper is given in Sect. 4.

2 An overview of sample selection models for count data

2.1 Model definition

In the sample selection problem, our aim is to fit a regression model when some observations of the outcome variable, $Y_{2i}$ for $i=1,\ldots ,n$, are missing not at random. We will use a latent continuous variable $Y_{1i}^*$ such that $Y_{1i}=\mathbf 1 (Y_{1i}^*>0)$, where $\mathbf 1$ is the indicator function and $Y_{1i}$ governs whether or not an observation on the variable of primary interest is generated. We assume normality for $Y_{1i}^*$ and a discrete distribution, ${\mathcal {F}}$, (see “Appendix 1” for all possible choices and Fig. 1 for illustration) for $Y_{2i}$. That is, $Y_{1i}^* \sim {\mathcal {N}}(\mu _{1i},1)$ (which yields a probit model for $Y_{1i}$) and $Y_{2i} \sim {\mathcal {F}}(\mu _{2i},\sigma _i, \nu _i)$, where $\mu _{1i}, \mu _{2i}$ are location parameters; $\sigma _i$ is the scale parameter and $\nu _i$ is the shape parameter. Note that we are considering parametrization for the most generic case of ${\mathcal {F}}$, although other parametrizations such as ${\mathcal {F}}(\mu _{2i})$ and ${\mathcal {F}}(\mu _{2i},\sigma _i)$ are possible.

We can represent the random sample using a pair of variables $(Y_{1i},Y_{2i})$. Let F denote the joint cumulative distribution function (cdf) of $(Y_{1i},Y_{2i})$ and let $F_{1}$ and $F_{2}$ be the marginal cdfs pertaining to $Y_{1i}$ and $Y_{2i}$, respectively. The model is then defined by using the copula representation (Sklar 1959)

$$\begin{aligned} F(y_{1i},y_{2i}) = C(F_{1}(y_{1i}), F_{2}(y_{2i}); \theta _i), \end{aligned}$$

for some two-place function C, where $\theta _i$ is an association parameter measuring the dependence between the two marginal cdfs. For details on binding continuous and discrete margins see Marra and Wyszynski (2016). In the presented package, the families currently implemented are normal, Clayton, Joe, Frank, Gumbel, Farlie–Gumbel–Morgenstern (FGM), and Ali-Mikhail-Haq (AMH; for examples of copulae, see Table 6 in “Appendix 1”). Rotations by 90, 180 and 270 degrees for Clayton, Joe and Gumbel can be obtained (see also Fig. 2 Brechmann and Schepsmeier 2013). Despite the fact that $\theta$ cannot be interpreted directly, it can be transformed into Kendall’s $\tau$ ranging on the interval $[-1,1]$ yielding a general interpretation for all copulae (for a discussion on Kendall’s $\tau$ for continuous and discrete margins see: Genest and Neslehova 2007; Marra and Wyszynski 2016).

Fig. 1

Probability mass functions of the Poisson (a), negative binomial (b), Delaporte (c) and Poisson inverse Gaussian (d) distribution. The parameter values have been chosen arbitrarily to show different shapes of the distributions. For Poisson, $\mu$ is 1, 2 and 5, represented as rectangular, circular and triangular lines respectively. Similarly, for negative binomial and Poisson inverse Gaussian, $\mu$ and $\sigma$ are (1, 1), (5, 2) and (30, 3). For Delaporte, $\mu$, $\sigma$ and $\nu$ are (1, 1, 0.1), (5, 2, 0.3) and (30, 3, 0.5). Note that Delaporte can have thinner or thicker tails depending on the choice of parameters. At the same time, the tails of Poisson are thinner than those of Delaporte (see: Marra and Wyszynski 2016)

Fig. 2

Contour plots of Frank (a), Joe (b), Clayton 90 (c) and Gumbel 270 (d) copulae. 5000 deviates were generated for each copula. The first margin is Poisson, whereas the second is standard normal. Kendall’s $\tau$ was set to 0.7. The plots have different shapes depending on the copula. For instance, Joe copula shows greater tail dependence in upper right corner, whereas Clayton 90 shows greater tail dependence in lower right corner (see: Marra and Wyszynski 2016)

The log-likelihood function for the sample selection model can be generically expressed as a product over two disjoint subsets of the sample: one for the observations with a missing value of the response of interest and the other for the remaining observations (Smith 2003). In the first case, the likelihood takes the simple form of $\Pr (Y_{1}=0)$, which is equivalent to $F_{1}(0)$. In the second case, the joint likelihood can be expressed, using the multiplication rule, as $P(Y_{2} = y_{2}, Y_{1} = 1)$. We dropped the observation index i to avoid clutter:

$$\begin{aligned} L= & {} \prod _{0}\Pr (Y_{1} = 0)\prod _{1}P(Y_{2} = y_{2}, Y_{1} = 1) \\= & {} \prod _{0}\Pr (Y_{1}^*\le 0)\prod _{1}f_{2|1}(y_{2}|y_{1}^*>0)\Pr (Y_{1}^*>0). \end{aligned}$$

Note that for the continuous response

$$\begin{aligned} f_{2|1}(y_{2}|y_{1}^{*}>0)= & {} \frac{\partial }{\partial y_{2}}\frac{F_{2}(y_{2})-F(0,y_{2})}{F_{1}(1)} \nonumber \\= & {} \frac{1}{1-F_{1}(0)}\frac{\partial }{\partial y_{2}}(F_{2}(y_{2})-F(0,y_{2})) \nonumber \\= & {} \frac{1}{1-F_{1}(0)}(f_{2}(y_{2})-\frac{\partial }{\partial y_{2}}F(0,y_{2})), \end{aligned}$$

(1)

and the log-likelihood will be

$$\begin{aligned} \ell= & {} \sum _{0} \log F_{1}(0) + \sum _{1} \log (f_{2}(y_{2})-\frac{\partial }{\partial y_{2}}F(0,y_{2}) ). \end{aligned}$$

In the third line of (1), for the discrete $y_{2}$, the derivative cannot be computed, since $F_{2}(y_{2})$ is discontinuous on the integers in its domain. We will calculate the derivative with respect to $y_{2}$ using finite differences (Nikoloulopoulos and Karlis 2009)

$$\begin{aligned} f_{2|1}(y_{2}|y_{1}^{*}>0)= & {} \frac{1}{1-F_{1}(0)}\{F_{2}(y_{2})-F_{2}(y_{2}-1)\}-\frac{1}{1-F_{1}(0)}\{F(0,y_{2})-F(0,y_{2}-1)\} \\= & {} \frac{1}{1-F_{1}(0)}\left[ \{F_{2}(y_{2})-F_{2}(y_{2}-1)\}-\{F(0,y_{2})-F(0,y_{2}-1)\}\right] \\= & {} \frac{1}{1-F_{1}(0)}\{F_{2}(y_{2})-F_{2}(y_{2}-1)-F(0,y_{2})+F(0,y_{2}-1)\}\\= & {} \frac{1}{1-F_{1}(0)}\{f_{2}(y_{2})-F(0,y_{2})+F(0,y_{2}-1)\}. \end{aligned}$$

The model log-likelihood will be given by (Marra and Wyszynski 2016)

$$\begin{aligned} \ell= & {} \sum _{0}\log F_{1}(0) + \sum _{1} \log (f_{2}(y_{2})-F(0, y_{2})+F(0, y_{2}-1)). \end{aligned}$$

(2)

Fig. 3

Modular relations between functions in SemiParSampleSel R package. The arrows indicate the direction in which the functions are called. For instance, SemiParSampleSel calls fit.SemiParSampleSel

Figure 3 illustrates how the main SemiParSampleSel function decomposes the likelihood in (2) in a modular fashion. The probability mass function, $f_{2}(y_{2})$, and cumulative distribution functions, $F_{1}(0)$, $F_{2}(y_{1})$ and $F_{2}(y_{1}-1)$, and their derivatives are obtained by marginBitsD. The copulae, $F(0, y_{2})$ and $F(0, y_{2}-1)$, and their derivatives with respect to cumulative distribution functions are computed with copulaBitsD. The ghssD function makes use of marginBitsD and copulaBitsD and constructs an object encompassing the likelihood of the sample selection model and its first and second derivatives. The univariate counterpart of the sample selection model, ghssDuniv, likewise utilizes information provided by marginBitsD. The parameter estimation is conducted by fit.SemiParSampleSel and both inputs and outputs are processed by SemiParSampleSel. Hence, one can implement potentially any margin or copula with great ease without changing the general structure of the likelihood. For instance, let us denote the parameters associated with the outcome linear predictor as $\varvec{\delta }_{2}$. The general expression of the first derivative of (2) with respect to $\varvec{\delta }_{2}$ is

$$\begin{aligned} \frac{\partial \ell }{\partial \varvec{\delta }_{2}}= & {} \sum _{1}\frac{1}{f_{2}(y_{2})-F(0,y_{2})+F(0,y_{2}-1)} \nonumber \\&\times \left( \frac{\partial f_{2}(y_{2})}{\partial \varvec{\delta }_{2}}-\frac{\partial F(0,y_{2})}{\partial F_{2}(y_{2})}\frac{\partial F_{2}(y_{2})}{\partial \varvec{\delta }_{2}}+\frac{\partial F(0,y_{2}-1)}{\partial F_{2}(y_{2}-1)}\frac{\partial F_{2}(y_{2}-1)}{\partial \varvec{\delta }_{2}}\right) , \end{aligned}$$

(3)

In this case, copulaBitsD will evaluate two derivatives and three derivatives will be processed by marginBitsD. The entire expression will be obtained via ghssD. Hence, implementing an additional copula or margin requires solely changes in either copulaBitsD or marginBitsD.

2.2 Linear predictor specification

We assume that the mean, scale, shape and copula parameters, $\mu _{1i}$, $\mu _{2i}$, $\sigma _{i}$, $\nu _i$ and $\theta _i$, are linked with the predictors $\eta _{vi}$, $v=1,\ldots ,5$, i.e., $\mu _{1i}=\eta _{1i}$, $g_{\mu }(\mu _{2i})=\eta _{2i}$, $g_{\sigma }(\sigma _{i})=\eta _{3i}$, $g_{\nu }(\nu _{i})=\eta _{4i}$ and $g_{\theta }(\theta _{i})=\eta _{5i}$, where the link functions g depend on the distributions of $y_{2i}$ and on the copula functions (see “Appendix 1”). For simplicity, and without loss of generality, we suppress the v subscript and define the generic linear predictor as

$$\begin{aligned} \eta _{i}=\mathbf u ^\mathsf{T}_{i}\varvec{\alpha }+ \sum _{k=1}^{K} s_{k}(z_{ki}), \ i=1,\ldots n, \end{aligned}$$

where vector $\mathbf u _{i}^\mathsf{T}=\left( 1,u_{2i},\ldots ,u_{Pi}\right)$ is the $i^{th}$ row of $\mathbf U =\left( \mathbf u _{1},\ldots ,\mathbf u _{n}\right) ^\mathsf{T}$, the $n\times P$ model matrix containing P parametric model components (e.g., intercept, dummy and categorical variables), $\varvec{\alpha }$ is a parameter vector, and the $s_{k}$ are unknown smooth functions of the K continuous covariates $z_{ki}$. The smooth functions are subject to the centering (identifiability) constraint $\sum _i s_{k}(z_{ki})=0$, $k=1,\ldots ,K$ (Wood 2017).

The smooth functions are represented using regression splines, where, in the one-dimensional case, a generic $s_k(z_{ki})$ is approximated by a linear combination of known spline basis functions, $b_{kj}(z_{ki})$, and regression parameters, $\beta _{kj}$, i.e., $s_k(z_{ki})=\sum _{j=1}^{J_k} \beta _{kj} b_{kj}(z_{ki})= \varvec{\beta }_{k}^\mathsf{T}\mathbf B _{k}(z_{ki})$, where $J_k$ is the number of spline bases used to represent $s_k$, $\mathbf B _{k}(z_{ki})$ is the $i^{th}$ vector of dimension $J_k$ containing the basis functions evaluated at the observation $z_{ki}$, i.e., $\mathbf B _{k}(z_{ki})=\left\{ b_{k1}(z_{ki}),b_{k2}(z_{ki}),\ldots ,b_{kJ_k}(z_{ki})\right\} ^\mathsf{T}$, and $\varvec{\beta }_{k}$ is the corresponding parameter vector. Calculating $\mathbf B _{k}(z_{ki})$ for each i yields $J_k$ curves (encompassing different degrees of complexity) which multiplied by some real valued parameter vector $\varvec{\beta }_{k}$ and then summed will give a (linear or non-linear) estimate for $s_k(z_{k})$ (see, for instance, Marra and Radice (2010) for a more detailed overview). Basis functions should be chosen to have convenient mathematical and numerical properties. B-splines, cubic regression and low rank thin plate regression splines are supported in our implementation (see Wood (2017) for full details on these spline bases). Our implementation also supports varying coefficients’ models, obtained by multiplying one or more smooth terms by some predictor(s), smooth functions of two or more (e.g., spatial) covariates, random effect and Markov random field smooth functions, to name but a few (Wood 2017). These cases follow a similar construction as described above. See, for instance, Wood (2017); Marra et al. (2017a).

In principle, the parameters of the sample selection model are identified even if the same regressors appear in both linear predictors (e.g., Wiesenfarth and Kneib 2010). However, better estimation results are generally obtained when the set of regressors in the selection equation contains at least one or more regressors (usually known as exclusion restrictions) that are not included in the outcome equation (e.g., Marra and Radice 2013).

2.3 Estimation approach

Unpenalized estimation can result in smooth term estimates that are too rough and overfitting (e.g., Wood 2017). This issue is dealt with by using a roughness penalty term (Ruppert et al. 2003; Wood 2017). Denote the log-likelihood function as $\ell (\varvec{\delta })$, where $\varvec{\delta }^\mathsf{T}=(\varvec{\delta }_1^\mathsf{T},\ldots , \varvec{\delta }_5^\mathsf{T})$. Note that this parameter vector’s definition is the most generic given the marginal distributions considered in this paper (this is consistent with zero inflated negative binomial, for instance). For outcome margins parametrized only in terms of $\mu$ (e.g., Poisson) we would have $\varvec{\delta }^\mathsf{T}=(\varvec{\delta }_1^\mathsf{T},\ldots , \varvec{\delta }_3^\mathsf{T})$, whereas for distributions parametrized in terms of both $\mu$ and $\sigma$ (e.g. beta binomial) we have $\varvec{\delta }^\mathsf{T}=(\varvec{\delta }_1^\mathsf{T},\ldots , \varvec{\delta }_4^\mathsf{T})$. For each smooth $s_{vk_{v}}(z_{vk_{v}})$ we have a penalty such that $\varvec{\beta }_{vk_{v}}^\mathsf{T}{{\mathbf {S}}}_{vk_{v}}\varvec{\beta }_{vk_{v}}$, where ${\mathbf {S}}_{vk_{v}}$ is a positive semi-definite penalty matrix with known coefficients. The quadratic expression is used, since it measures the second-order roughness of the smooth terms in the model. The form of the penalty ${\mathbf {S}}_{vk_{v}}$ will depend on the selected spline basis (Wood 2017). The function to maximize is

$$\begin{aligned} \ell _p(\varvec{\delta })= \ell (\varvec{\delta }) -\frac{1}{2} \varvec{\delta }^\mathsf{T}\mathbf S _{\varvec{\lambda }} \varvec{\delta }. \end{aligned}$$

(4)

where ${\mathbf {S}}_{\varvec{\lambda }}=\mathop {\mathrm {diag}}(\varvec{0}_{P_{1}}^\mathsf{T}, \lambda _{1k_{1}}{\mathbf {S}}_{1k_{1}}, \ldots , \lambda _{1K_{1}}{\mathbf {S}}_{1K_{1}}, \varvec{0}_{P_{2}}^\mathsf{T}, \lambda _{2k_{2}}{\mathbf {S}}_{2k_{2}},\ldots , \lambda _{2K_{2}}{\mathbf {S}}_{2K_{2}}, \varvec{0}_{P_{3}}^\mathsf{T}, \lambda _{3k_{3}}{\mathbf {S}}_{3k_{3}}, \ldots , \lambda _{3K_{3}}{\mathbf {S}}_{3K_{3}}, \varvec{0}_{P_{4}}^\mathsf{T},$ $\lambda _{4k_{4}}{\mathbf {S}}_{4k_{4}}, \ldots , \lambda _{4K_{4}}{\mathbf {S}}_{4K_{4}}, \varvec{0}_{P_{5}}^\mathsf{T}, \lambda _{5k_{5}}{\mathbf {S}}_{5k_{5}}, \ldots , \lambda _{5K_{5}}{\mathbf {S}}_{5K_{5}})$ in the most generic case; $\lambda _{vk_{v}}$ represents smoothing parameters which control for the trade-off between fit and smoothness.

The estimation algorithm is structured in two main steps which are iterated until convergence:

Step.1:

For a given vector $\varvec{\delta }^{[a]}$, and maintaing smoothing parameter fixed at $\varvec{\lambda }^{[a]}$, find the new iterate for $\varvec{\delta }$ using trust region approach (Chapter4 Nocedal and Wright 2006):

where $\Vert \cdot \Vert$ denotes the Euclidean norm and $r^{[a]}$ represents the radius of the trust region. After dropping the iteration index, the score vector $\mathbf g$ is defined by five subvectors $\mathbf g _{o}=\partial \ell (\varvec{\delta }) /\partial \varvec{\delta }_{o}$ for $o=1,\ldots ,5$, while the Hessian matrix has a $5 \times 5$ matrix block structure with $(r,h)^{th}$ element $\varvec{\mathcal {H}}_{r,h}=\partial ^2 \ell (\varvec{\delta })/\partial \varvec{\delta }_r \partial \varvec{\delta }_h^\mathsf{T}$, $r,h=1,\ldots ,5$. At each iteration of the algorithm, $\breve{\ell _p}(\varvec{\delta }^{[a]})$ is minimized subject to the constraint that the solution falls within a trust region with radius $r^{[a]}$. The proposed solution is then accepted or rejected and the trust region expanded or shrunken based on the ratio between the improvement in the objective function when going from ${\varvec{\delta }}^{[a]}$ to ${\varvec{\delta }}^{[a+1]}$ and that predicted by the quadratic approximation. Note that, near the solution, the trust region Newton algorithm typically behaves as a Newton algorithm (Chapter 4 Nocedal and Wright 2006).

Step 2:

For a given smoothing parameter vector value $\varvec{\lambda }^{[a]}$, and maintaining $\varvec{\delta }^{[a+1]}$ fixed, find an estimate of $\varvec{\lambda }$:

$$\begin{aligned} \text {minimize} \ \ \frac{1}{n^*}||\sqrt{\mathbf {W}}({\mathbf {z}}-{\mathbf {X}}\varvec{\tilde{\delta }}) ||^{2} - 1 + \frac{2}{n^*}\mathrm{tr}\left( {\mathbf {A_{\varvec{\lambda }}}} \right) \ \ \text { w.r.t. }\ \ \varvec{\lambda }, \end{aligned}$$

(5)

where $\sqrt{\mathbf{W}}$ is a weight non-diagonal matrix square root, $\mathbf z$ is the pseudo-data vector consisting of 5-dimensional subvectors $\mathbf z _i$ defined as $\mathbf z _i=\mathbf X _i \varvec{\delta }^{[a]}+\mathbf W _i^{-1}{} \mathbf d _i$, $\mathbf d _i=\left\{ \partial \ell (\varvec{\delta })_i/ \partial \eta _{1i}, \ldots ,\partial \ell (\varvec{\delta })_i/ \partial \eta _{5i}\right\} ^\mathsf{T}$, $\mathbf W _i$ is a $5 \times 5$ matrix with $(r,h)^{th}$ element $\left( \mathbf W _i\right) _{rh}=-\partial ^2 \ell (\varvec{\delta })_i/\partial \eta _{ri}\partial \eta _{hi}$, $r,h=1,\ldots ,5$, $\mathbf X _i=\text {diag}\left\{ \left( \mathbf u ^\mathsf{T}_{1i},\mathbf B _{1i}^\mathsf{T}\right) ,\ldots ,\left( \mathbf u ^\mathsf{T}_{5i},\mathbf B ^\mathsf{T}_{5i}\right) \right\}$, $\varvec{\tilde{\delta }} = \left( {\mathbf {X}}^\mathsf{T}{\mathbf {W}}{\mathbf {X}} + {\mathbf {S_{\varvec{\lambda }}}}\right) ^{-1}{\mathbf {X}}^\mathsf{T}{\mathbf {W}}{\mathbf {z}}$, $n_*=5n$, $\sqrt{\mathbf {W}}{\mathbf {A}}=\sqrt{\mathbf {W}}{\mathbf {X}}\left( {\mathbf {X}}^\mathsf{T}{\mathbf {W}}{\mathbf {X}} + {\mathbf {S_{\varvec{\lambda }}}}\right) ^{-1}{\mathbf {X}}^\mathsf{T}{\mathbf {W}}$ is the hat matrix, and $\text {tr}(\mathbf A _{\varvec{\lambda }})$ the estimated degrees of freedom (edf) of the penalized model (e.g., Marra and Wyszynski 2016). The iteration index has been dropped to avoid clutter. We will use the approach by Wood (2004) to perform minimization of (5), which turns out to be computationally efficient and stable.

2.4 Confidence intervals, variable and model selection

Inferential theory for penalized estimators is complicated by the presence of smoothing penalties which undermines the usefulness of classic frequentist results for practical modeling. As shown in Marra and Radice (2013), reliable pointwise confidence intervals for the terms of a regression spline sample selection model can be constructed using

$$\begin{aligned} \varvec{\delta }|\mathbf{z} \dot{\backsim } {\mathcal {N}}(\hat{\varvec{\delta }},\mathbf{V}_{\varvec{\delta }}), \end{aligned}$$

(6)

where $\hat{\varvec{\delta }}$ is an estimate of $\varvec{\delta }$ and $\mathbf{V}_{\varvec{\delta }} = (-\varvec{\mathcal {H}}+\mathbf{S}_{\hat{\varvec{\lambda }}})^{-1}$. The structure of $\mathbf{V}_{\varvec{\delta }}$ is such that it includes both a bias and variance component in a frequentist sense, which is why such intervals exhibit close to nominal coverage probabilities (Marra and Wood 2012). Given (6), confidence intervals for linear and non-linear functions of the model parameters can be easily obtained. For instance, for a generic $\hat{s}_k(z_{ki})$ these can be obtained using

$$\begin{aligned} \hat{s}_k(z_{ki}) \dot{\backsim } {\mathcal {N}}(s_k(z_{ki}),\mathbf B _k(z_{ki})^\mathsf{T}\mathbf{V}_{\varvec{\delta }_{k}}{} \mathbf B _k(z_{ki})), \end{aligned}$$

where $\mathbf{V}_{\varvec{\delta }_{k}}$ is the submatrix of $\mathbf{V}_{\varvec{\delta }}$ corresponding to the regression spline parameters associated with $k^{th}$ function. Intervals for non-linear functions of the estimated model coefficients can be conveniently obtained by simulation from the posterior distribution of $\varvec{\delta }$. As for the parametric model components, using (6) is equivalent to using classic likelihood results because such terms are not penalized. Intervals for average values of $\sigma$, $\nu$ and $\theta$ can be obtained by simulating from the posterior distribution of $\varvec{\delta }$ as follows:

• 1. Draw $n_{sim}$ random vectors from (6).

• 2. Calculate $n_{sim}$ simulated realizations of the function of interest. For example, since $g_{\sigma }(\sigma _{i})=\eta _{3i}$, $\varvec{\sigma }_{i}^{sim}=(\sigma _{1i}^{sim}, \sigma _{2i}^{sim}, \ldots , \sigma _{n_{sim}i}^{sim})$ where $\sigma _{o i}^{sim}=g_{\sigma _{i}}^{-1}(\eta _{3oi}^{sim})$, $o=1,2,\ldots ,n_{sim}$. For each o, obtain the mean value of $\sigma _{o i}^{sim}$ across all observations.

• 3. Using $\varvec{\sigma }^{sim}$, calculate the lower, $\xi /2$, and upper, $1-\xi /2$, quantiles. For 95 per cent Bayesian confidence intervals, $\xi$ is set to 0.05.

Copula models with a single dependence parameter can be thought of as non-nested models. As suggested by Zimmer and Trivedi (2006) among others, one approach for choosing between copula models is to use either the Akaike or (Schwarz) Bayesian information criterion ($\textit{AIC}$ and $\textit{BIC}$, respectively). In our case, $\textit{AIC}=-2\ell (\hat{\varvec{\delta }})+2edf$ and $\textit{BIC}=-2\ell (\hat{\varvec{\delta }})+\log (n)edf$, where the log-likelihood is evaluated at the penalized parameter estimates and $edf=\text {tr}(\hat{\mathbf{A }}_{\hat{\varvec{\lambda }}})$. Other model selection methods include Vuong and Clarke test (Vuong 1989; Clarke 2007), which will be illustrated in the next section.

3 The package SemiParSampleSel

As pointed out above, the R package SemiParSampleSel implements model-based penalized maximum likelihood estimation that results in interpretable models. As mentioned in Sect. 2.1, the SemiParSampleSel package offers a modular nature that allows to specify a wide range of non-random selection models. The non-random sample selection model is specified as the combination of a distributional assumption and structural assumptions. Unlike in the case of Greene (1997), the distributional assumption specifies the conditional distribution of the outcome. The structural assumption specifies the types of effects that are to be used in the model, i.e., it represents the deterministic structure of the model. Usually, it specifies how the predictors are related to the conditional mean, variance and shape of the outcome variable and how the selection mechanism and the outcome are related.

The function SemiParSampleSel() provides an interface to fit sample selection models for continuous and count data. Before we show how one can use the function to fit this model to estimate the determinants of labor mobility, we give a short overview on the function:

The model is specified using a formula which is a list of five formulas, one for the mean of the selection equation, three for the mean, variance and shape of the outcome equation and one for the copula parameter. These are glm() like formulas except that smooth terms can be included in the equations as for gam() in mgcv. For instance, the formulas for the mean of the selection equation may look like:

and that for the scale parameter of the outcome equation:

where y.sel represents the binary selection variable, x1 is a categorical predictor, and the s() terms are used to specify smooth functions of the continuous predictors x2, x3 and x4. Argument bs specifies the spline basis; possible choices include cr (cubic regression spline), cs (shrinkage version of cr), tp (thin plate regression spline) and ts (shrinkage version of tp). Bivariate smoothing, e.g., s(x3, x4), is achieved using bs = “tp”. k is the basis dimension (default is 10) and m the order of the penalty (default is 2). More details and options on smooth term specification can be found in the documentation of mgcv. SemiParSampleSel does not currently support the use of tensor product smooths. The data set is provided as a data.frame via the data argument. The type of bivariate copula linking the selection and outcome equations can be specified through BivD. Possible choices are “N”, “C0”, “J0”, “FGM”, “F”, “AMH” and “G0” which stand for bivariate normal, Clayton, Joe, Farlie-Gumbel-Morgenstern, Frank, Ali-Mikhail-Haq and Gumbel. Rotated versions (90, 180 and 270 degrees) of the asymmetric copulae are also implemented (“C90”, “C180”, “C270”, “J90”, ...). For more details on available copulae see “Appendix 1”. The argument margins specifies the marginal distributions of the selection and outcome equations, given in the form of a two-dimensional vector which is equal to c(“probit”,“NB”) for normal and negative binomial margins. The first margin currently admits only the normal distribution (“probit”). The second margin can also be “N”, “GA”, “NB”, “D”, “PIG” or “S” which stand for normal, gamma, negative binomial, Delaporte, Poisson inverse Gaussian and Sichel (see “Appendix ”). Details on all the other arguments, including starting value and control options, and the fitted-object list that the function returns can be found in Marra et al. (2017b). See also data simulation function in Appendix 2, for example.

Apart from SemiParSampleSel(), the package also encompasses several other functions, which offer some numerical and graphical interpretations. These will be presented in the next section:

• resp.check(y, margin = “P”). This function preliminarily checks whether the (non-missing) response follows one of the discrete distributions. This is done by generating a kernel density and normalized and randomized QQ-plot (for details see: Stasinopoulos and Rigby 2007). Distributions that require a binomial denominator (e.g., binomial) need to specify bd as an argument.

• conv.check() provides some information about the convergence of the algorithm.

• summary(). The summary function of SemiParSampleSel(); analogical to the one in glm and gam.

• AIC() and BIC() return Akaike and Bayesian information criteria.

• VuongClarke() performs Vuong and Clarke test for comparing two competing models. For example, these can be models that differ on the choice of copula.

• aver() provides the average predicted values for the entire data set. When univariate = TRUE, the average prediction for the univariate model ignoring non-random sample selection is returned.

• plot() function illustrates smooth terms when they are specified for a given equation. For instance, eq = 1 will yield a smooth function for the selection equation of the model.

• post.check() takes the response vector and produces a QQ-plot based on the estimates obtained from the sample selection model. Simlarly to resp.check(), the residuals are normalized and randomized. Distributions that require a binomial denominator need to specify bd as an argument.

3.1 Case study: an application to labor mobility

The data is from the German Socio-Economic Panel survey of 1984 (SOEP v28 2012) and the aim of the study is to estimate the determinants of labor mobility in the presence of non-random sample selection. As mentioned in the introduction, non-random selection arises if the sample consisting of individuals who are on the job market differ in important characteristics from the sample of individuals who are not part of the job market. To rectify this situation, we will employ sample selection models implemented in SemiParSampleSel.

We first load the package and the data set.

The data set contains 2,651 observations and the outcome variable is the number of direct job changes (DJC, i.e. changes without an intervening spell of unemployment). Other available variables are presented in Table 1.

Table 1 Variables of SOEP data

Following the work by Winkelmann (1998), the linear predictors for the selection and outcome equations, respectively, can be specified as follows

$$\begin{aligned} \begin{aligned} \eta _1&= \alpha _{10}+ \alpha _{11}{} \texttt {Single} + \alpha _{12}{} \texttt {WhiteCollar} + s_{11}(\texttt {EXPFT}) \\ \eta _2&= \alpha _{20} + \alpha _{21}{} \texttt {SPDSup} + \alpha _{22}{} \texttt {WhiteCollar} + s_{21}(\texttt {LEduc}), \end{aligned} \end{aligned}$$

where the non-linear specification of LEduc and EXPFT arises from the fact that these covariates embody productivity and life-cycle effects that are likely to affect the probability to be part of the job market non-linearly. These will be modeled using thin plate regression splines with 10 bases and penalties based on second order derivatives. We will employ linear predictors for the scale and association parameters, since WhiteCollar may have an impact on variability of the response. Thus,

$$\begin{aligned} \begin{aligned} \eta _3&= \alpha _{30} + \alpha _{31}{} \texttt {WhiteCollar} \\ \eta _4&= \alpha _{40} + \alpha _{41}{} \texttt {WhiteCollar}, \end{aligned} \end{aligned}$$

In R, the specification above implies determining formulas as

Prior to fitting a count data sample selection model, a distribution for the outcome variable may be chosen by looking at the histogram of the response along with the estimated density from the assumed distribution, and at the randomized and normalized responses (Rigby and Stasinopoulos 2005). The latter will provide an approximate guide to the adequacy of the chosen distribution. These should behave approximately as normally distributed variables (even though the original observations are not). Note that this preliminary check has to be treated with caution, since the distribution of the outcome is assumed to be unconditional on any covariate effects.

These plots (reported in Fig. 4; for the remainder see Appendix 3) show that the density and QQ-plots are the most supported with “PIG” being the best. Based on this, we fit the count sample selection model with Poisson inverse Gaussian margin for the outcome variable using the function SemiParSampleSel() to the SOEP data. The normal copula is used to link the selection and the outcome equations. The reason for choosing normal copula is to preliminarily check the direction and magnitude of association between both equations.

Fig. 4

Poisson inverse Gaussian kernel density and QQ-plot

Before viewing the output, it is necessary to check the convergence of the algorithm. This can be done by submitting conv.check() command.

The algorithm converged successfully, since the gradient is equal to zero and the Hessian is positive definite. Note that the condition number is equal to $\frac{5477.451}{0.4848655} \approx 10^{4}$. The summary() function yields

The output shows all estimates pertaining to the selection and outcome equations, and the equations linked with the scale and association parameters. In particular, the white-collar effect on the selection is statistically significant and implies that white-collar workers are more likely to be active on the labour market than non-white-collar workers. In addition, the white-collar effect on the outcome is also statistically significant and suggests that being a white-collar worker decreases chances of changing jobs and hence labour mobility. At the bottom of the output one can see the mean values across all observations for $\hat{\sigma }$ and $\hat{\theta }$ together with the corresponding confidence intervals.

Let us estimate a Poisson inverse Gaussian Frank (fit2) and Joe 270 (fit3) models with the same specification as the normal Poisson inverse Gaussian. The Akaike and Bayesian information criteria to compare the competing models are obtained using AIC() and BIC() functions.

The left-hand side column indicates the estimated degrees of freedom, whereas the right-hand side denotes the criterion. Table 2 shows the AIC and BIC scores for the normal Poisson inverse Gaussian model and other Poisson inverse Gaussian models with different copulae. These are Frank and the 90 and 270 degrees rotated versions of Joe, Gumbel and Clayton. The reason for choosing these rotations is that the normal model initially indicated negative dependence of $\hat{\theta } = -0.761$ and these rotations envisage negative dependence. The differences in AIC and BIC are small. Nevertheless, the best-performing model in accordance with both criteria turns out to be Frank, Joe 270 and Clayton 90. Hence, these models may be considered if the modeler is interested in making predictions of the number of job changes.

Table 2 Akaike and Bayesian information criteria for the Poisson inverse Gaussian models for SOEP data

Alternatively, one can use the Vuong test to compare between two competing models. The VuongClarke() function returns

By default, the significance level was set to 0.05. The Vuong test does not indicate any preferred model. On the other hand, Clarke test prefers Frank over Joe 270 model.

We will carry out the remainder of the analysis using Frank model. The average predictions for all observations are obtained by

The former statement returns an average prediction for the univariate model ignoring non-random sample selection; the latter returns an average prediction for the sample selection model. To extract the association parameters with their corresponding confidence bounds one needs to submit

Table 3 summarizes the corresponding average predictions and association parameters of the univariate, normal, Frank, and the rotated versions of Clayton, Joe and Gumbel models. The values in brackets indicate 95% confidence interval bounds. For all models, the confidence intervals of $\hat{\theta }$ do not reach their bound, which implies that non-random sample selection is likely to be present. Note that Kendall’s $\hat{\tau }$ indicates a strong negative correlation between the selection and the outcome. The average predictions do not differ substantially from another. In fact, the confidence intervals of most of the models overlap. Thus, the copula assumption does not seem to have a major impact on the predictions for sample selection models.

Table 3 Average predictions of job changes and estimates of association parameters for Delaporte model and Frank, and 90 and 270 degrees rotated Clayton, Joe and Gumbel

The post-estimation QQ-plots can be obtained by submitting the following command line

Figure 5 shows post-estimation QQ-plots based on estimates from the Poisson inverse Gaussian sample selection model with Frank copula. Note that the plot is similar to the one in Fig. 4 and hence the model provides a good fit to the data.

Fig. 5

QQ-plot for Poisson inverse Gaussian and Frank copula

The smooth plots for both equations can be obtained by submitting the following command lines

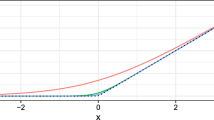
Figure 6 shows the smooths for the continuous covariates EXPFT (left) and LEduc (right). The selection equation smooth can be interpreted such that the likelihood of being active on the labor market as a dependent worker increases when gaining full time work experience. Then, the likelihood of being active gradually decreases as individuals start to receive pensions or enter into self-employment. The outcome smooth suggests that the longer the education of an individual lasts the less likely he is to change his job. This is due to increasing specialization in his professional area as he becomes more qualified. Therefore, it is harder for him to find an alternative occupation or there are no financial incentives for changing jobs (e.g. medical doctors).

Fig. 6

Selection (left) and outcome (right) equation smooth for Poisson inverse Gaussian outcome and Frank copula

To obtain each $\sigma _{i}$ and $\tau _{i}$ (and the corresponding 95 per cent confidence intervals) one needs to submit fit2$sigma and fit2$tau (summary(fit2)$CIsig.1 and summary(fit2)$CIkt.1). The confidence intervals for white-collars and non-white-collars given each parameter are visualized in Fig. 7. For instance, since the confidence interval for white-collars in $\tau$ overlaps with zero, for the group of white-collar workers non-random sample selection is likely to be absent.

Fig. 7

Point estimate plots with the corresponding confidence intervals for white-collar workers (WhiteCollar = 1; left) and non-white-collar workers (WhiteCollar = 0; right). The left-hand panel depicts the plot for $\sigma$ and the right-hand plot for $\tau$

4 Summary

In this paper, we introduced the new features of SemiParSampleSel R package. The functions included in the package can be used to estimate sample selection models for a wide selection of discrete responses and incorporate flexible covariate effects. The modeling approach allows for a specification of the bivariate distribution using copulae. By doing so, the modeler can check the assumption of bivariate normality.

The function resp.check() allows the modeler to perform exploratory analysis on the non-missing response permitting the distributional assumption of the outcome to be checked. SemiParSampleSel() can be used to estimate the model under the desired specification, whereas the summary() function returns the output. aver() function calculates the average prediction of the univariate and sample selection model for all observations. AIC(), BIC() and VuongClarke can be used for choosing between two competing models; post.check() creates post-estimation QQ-plots and plot() returns smooth plots for equations, where continuous covariates were specified in terms of splines.

The approach can be extended to trivariate system models. These account for the endogeneity of a treatment variable and for non-random sample selection in the outcome. Also, copulae with two parameters can be introduced - these would lead to a better control of tail-dependence, despite the risk of association parameters losing their interpretation (e.g., Brechmann and Schepsmeier 2013).

In the context of selection margin, one could employ skew probit links as derived from the standard skew-normal distribution by Azzalini (1985). Introducing a parameter which regulates the distribution’s skewness may have very attractive properties from the probability point of view (Azzalini and Arellano-Valle 2013).

Future research may also involve applying the new SemiParSampleSel functions to problems in other fields. For instance, Greene (1998) estimates a sample selection model for predicting the number of non-payments by individuals who own a credit card. In this case, individuals select themselves into the sample of credit card owners based on observed characteristics (such as gender and age) and unobserved ones (e.g. unreported income). In particular, it would be of interest to explore how average predictions change if non-random sample selection is accounted for.

Another application involves patients who are newly-referred to a specialist doctor by a general practitioner and often have to be assessed using ultrasound imaging devices (Ciurtin et al. 2016). In many circumstances, public health systems cannot afford an assessment of every patient. Non-random sample selection may be present in the assessment scores, since patients are referred based on characteristics that cannot be accounted for e.g. fatigue of the consultant or patient’s personality. To rectify this situation, sample selection models can be applied.

Appendices

Appendices

1.1 1 Margins and copulae implemented in SemiParSampleSel

See Tables 4, 5 and 6.

Table 4 Discrete distributions implemented in SemiParSampleSel R package. The parameter ranges corresponding to log, logit and identity links are $(0, \infty )$, [0, 1] and $(-\infty , \infty )$. For binomial-type distributions, the binomial denominator is determined by the modeler. Note that the support of the logarithmic distribution does not include zero

Table 5 Zero-inflated and zero-altered discrete distributions implemented in SemiParSampleSel R package

Table 6 Examples of families of bivariate copulae

1.2 2 Data simulation function

For reader’s interest, we also provide a code for simulating data suffering from non-random sample selection for Poisson, negative binomial, Delaporte, Poisson inverse Gaussian and Sichel distributions. The potential copulae include the ones mentioned in Table 6. The list of possible outcomes and copulae is not exhaustive and can be extended. In the case below, two covariates are simulated which enter both the selection and outcome equation. n stands for the number of observations to be generated, s.tau is correlation between the outcome and the selection equation defined in terms of Kendall’s tau, rhC is the Pearson correlation correlation coefficient for the covariates; outcome.margin and copula are the outcome margin and copula defined by the user.

For instance, to simulate data and estimate a sample selection model with Poisson margin and Frank copula one needs to submit the following code

1.3 3 Preliminary analysis plots

See Fig. 8

Fig. 8

Poisson (a), negative binomial (b), Delaporte (c) and Sichel (d) QQ-plots