Investigation of the effect of raster angle, build orientation, and infill density on the elastic response of 3D printed parts using finite element microstructural modeling and homogenization techniques

Abstract

Although the literature is abundant with the experimental methods to characterize mechanical behavior of parts made by fused filament fabrication 3D printing, less attention has been paid in using computational models to predict the mechanical properties of these parts. In the present paper, a numerical homogenization technique is developed to predict the effect of printing process parameters on the elastic response of 3D printed parts with cellular lattice structures. The development of finite element computational models of printed parts is based on a multi scale approach. Initially, at the micro scale level, the analysis of micro-mechanical models of a representative volume element is used to calculate the effective orthotropic properties. The finite element models include different infill densities and building/raster orientation maintaining the bonded region between the adjacent fibers and layers. The elastic constants obtained by this method are then used as an input for the creation of macro scale finite element models enabling the simulation of the mechanical response of printed samples subjected to the bending, shear, and tensile loads. Finally, the results obtained by the homogenization technique are validated against more realistic finite element explicit microstructural models and experimental measurements. The results show that, providing an accurate characterization of the properties to be fed into the macro scale model, the use of the homogenization technique is a reliable tool to predict the elastic response of 3D printed parts. The outlined approach provides faster iterative design of 3D printed parts, contributing to reducing the number of experimental replicates and fabrication costs.

1 Introduction

Due to the recent advances in additive manufacturing (AM) technology, lightweight parts with complex geometries have seen an increased popularity in sectors such as automotive, aerospace, military, marine, and biomedical and the electronics industries. Among these lightweight parts, 3D printed structures with cellular lattice are of special importance as the desirable mechanical properties can be obtained by designing appropriate microstructures. In fused filament fabrication (FFF), a very popular technique in AM for rapid prototyping, the lightweight components with the cellular lattice structures can be printed through the extrusion of filament material in a layer-by-layer deposition process. Although in these methods lattice structures with the high repeatability can be fabricated, it is important to characterize their mechanical properties in order to ensure the in-service performance requirements are met. The layer-by-layer deposition in FFF creates material microstructures different from traditional manufacturing methods. Different FFF process parameters such as build and raster orientations, layer height, filament width, and infill patterns and densities can significantly affect the mechanical properties of printed parts. Although in the literature experimental analysis using design of experiments have been developed to investigate the effect of processing parameters on the mechanical behavior of 3D printed parts with internal lattice structures [1, 2], the materials’ uncertainty and variability, as well as time and cost of the experimental procedure, are challenging issues.

Recently new approaches have been introduced in the literature in order to achieve maximum functional performance in additive manufacturing [3] where “replicative” structures in different sizes and orders of magnitude are used to manufacture parts with the minimum weight but achieving the required mechanical properties. The effect of feed rate using an algorithm for homogeneous material deposition was also investigated and, as a result, the importance of process control in the direct manufacturing processes of components was highlighted [4]. Although the above studies have been successful in producing parts with complex geometries whose total weight is minimized while their mechanical strength is optimized, the use of topology and lattice optimization by employing numerical methods (e.g., finite element modeling) is less well-developed currently and is high priority for research. This is mainly due to the use of additive manufacturing (3D printing) in a wider range of industries to achieve cost reductions with material savings. Therefore, analytical and numerical methods with the ability to predict the mechanical properties of 3D printed structures are required resulting in a significant reduction in the number of experimental procedures, associated costs, and time to market.

In terms of modeling with either analytical or semi-analytical methods, classical laminate theory (CLT)–based approaches have been developed to characterize the behavior of printed structures. The use of CLT combined with experimental characterization to study the mechanical properties of FFF-based 3D printed parts has resulted in successful prediction of the elastic constants [5,6,7,8]; however, the approach is limited to parts fabricated with 100% infill density meaning that no separation between the deposited filaments is assumed (i.e., the mechanical response of structures with partial infill cannot be estimated based on CLT approaches). In addition, in the aforementioned works, the effects of build orientation on mechanical behavior of printed parts as well as the effect of internal features of meso-structures are not taken into consideration. To address this, micromechanics-based approaches focusing on the analysis of a repeating unit cell have been developed [9,10,11,12], and this has resulted in the derivation of analytical expressions for the structure-property relationships.

Due to the complex microstructures and inherent anisotropic mechanical behavior of parts obtained by FFF and also because of the many process parameters involved, computational simulation using finite element analysis (FEA) has been found to be useful when estimating the structural performance. In FFF-based 3D printed parts that have cellular lattice structures, FE models have been used to study the effect of different infill patterns [13] and infill densities [14] on the mechanical behavior of parts, to interpret anisotropic damage occurring during severe compression loading [15], to predict the anisotropy induced by 3D printing [16], and to evaluate the effect of microstructural defects by analyzing the stress/strain fields for different build orientations [17]. Among the different FE-based approaches, the use of space frame and shell models to predict the linear elastic behavior of the printed parts has received particular attention in the literature. For example, it has been shown that a beam-based FE model can predict the elastic modulus with good accuracy [18]. Using the same approach [19], it was found that FE-computed mechanical properties of cellular lattice structures (with the layers of filaments laid up at ±45° alternately) are in good agreement with tensile, compressive, and shear tests of 3D printed specimens. In another work [20], a frame FE model was used to analyze the effect of infill design of printed parts and it was found that for the optimized part the FE calculated structural response was in good agreement with experiment. In addition, it has been shown that the use of frame-based FE modeling is not only limited to FFF-based 3D printing structures, but also it is applicable in other AM to estimate the mechanical properties [21, 22]. The main issue of using space frame and shell FE model is the efficiency, when the number of elements increases, and the consequent analysis can become computationally very expensive. To address this, a homogenization-based approach has been developed. Analytical and numerical methods of homogenization to predict the mechanical response of 3D printed and composite structures have been investigated thoroughly in the literature [23,24,25,26,27,28,29], and the results show that representative volume-based FE model is a good option for modeling of such parts with regular repeating cellular lattice structures; however, attention must be paid to consider the effect of boundary conditions and border effects. In fact, when it comes to the FEA of 3D-printed cellular structure using virtual experiments, in order to exploit the advantage of using homogenization procedures and therefore avoiding the computationally expensive explicit microstructural modeling, the size of representative volume element (RVE) should be large enough, such that the effective properties will not depend on the boundary conditions and border effects. The chosen RVEs, however, should not be very large to make the computational modeling too expensive [30]. A reference for the size of RVEs when it comes to the virtual experiments and homogenization procedures of 3D printed parts is the micromechanical analysis of stochastically distributed short fiber–reinforced polymer composites where a cube with side of 50 times bigger than the size of individual fiber is considered adequately large RVE [31].

In the FE homogenization technique, the prediction of effective macro-scale material properties is based on the constituent’s properties (i.e., the virgin materials used for printing) and geometrical features of the microstructure. In this technique, the printed part is considered a continuum and a small volume element (unit cell) which periodicity fills the 3D printed part is considered for numerical homogenization. This periodic unit cell is known as RVE. Usually, a two-step homogenization approach is used for the analysis of 3D printed structures [28]. In this method, estimated effective engineering constants are used for subsequent mechanical simulation of global elastic response. Experimental characterization via tensile testing is carried out to obtain the orthotropic elastic constants of FFF printed samples [32]. In this study, the properties obtained from experiments were used as an input into the FE models to estimate the structural response of elements and a good agreement between FEA predictions and experimental data was obtained. In different works [33, 34], the authors developed FE models of the RVE which was subjected to tensile and shear loading, and then homogenized engineering constants obtained from the analysis of the RVE were used for the FE analysis of structures with more complex design.

Although the homogenization procedure can make accurate prediction of the macro-scale properties of 3D printed parts from the micro-scale properties of their constituents, the use of this technique is limited when accounting for the effect of important features of micro mechanics such as stress localization which is important for predicting the local failure mechanisms. To address this, FE explicit microstructural modeling formed by extruded filaments have been used in some studies [12, 35, 36]. The CAD models built by this type of geometry modeling are more like the real microstructure of 3D printed parts; however, this method is computationally expensive due to the increased number of elements required for meshing.

In the present study, the FE homogenization approach is applied to generate homogenized mechanical properties for the internal cellular lattice structures of FFF-based 3D printed parts. The RVE of the lattice structure was analyzed by the FE method to determine the bulk properties of 3D printed parts. Then, the obtained properties were used for the subsequent mechanical simulation of printed bending, shear, and tensile testing samples where the effect of different processing parameters was also investigated. Although previous studies have used this technique to predict the elastic response of 3D printed parts, the present study focuses on the experimental validation of the FE results (both homogenization and explicit microstructural modeling methods). In addition, capturing the effect of raster angle, build orientation and infill density using the FE methodologies used in the present work is a previously unexplored research area. In the present study, the use of a micromechanics plugin in the FE software ANSYS (material designer) integrated with ANSYS Composite Pre-Processor (ACP) allowed the definition of different layer thicknesses as well as build/raster orientations; therefore, the effect of these parameters was considered in the simulation. Compared to the lattice FE model, the homogenized continuum FE model uses a much lower number of elements. While reducing the FEA time, the homogenization-based approach can effectively estimate the elastic behavior of 3D printed parts. This would enable engineers and manufacturers in many sectors (e.g., automotive, aerospace, and biomedical (implants) industries) to use a mathematical methodology (such as topology and lattice optimization tools) to optimize material layout within a given design space, for a given set of masses and loads, materials, and boundary conditions as well as constraints with the objective of maximizing performance (quasi static and dynamic mechanical behavior) of the system. This will help designers to conduct iterative analysis and select process parameter settings to optimize the shape and the density of infill for FFF-based 3D printed parts.

2 Methodology

2.1 Sample preparation and mechanical testing

In this study, in order to validate the FE simulation results of 3D printed tensile, shear, and three-point bending (3PB) testing, specimens were produced using a fused filament fabrication (FFF) 3D printer (Ultimaker 3), and then mechanical testing in conjunction with digital image correlation (DIC) detailed in [37] was carried out to obtain the full field strain maps and the stress-strain curves. A polylactic acid (PLA) filament provided by Ultimaker (standard silver metallic PLA, 2.85 mm/750 gram) was used to obtain the 3D printed specimens. The Ultimaker Cura 4.8 edition was used to generate the machine code for the FFF 3D printer from the 3D model files. Simple 3D printed test sample designs based on ASTM standards were used in all cases. The geometry and dimension of the tensile, Iosipescu, 3PB, and inter-laminar shear (ILS) test specimens are in accordance with ASTM D638, ASTM D5379, ASTM D7264, and ASTM D2344 standards respectively [38,39,40,41]. The 3D printing process parameters used to produce the test specimens are provided in Table 1. In order to examine the effect of raster and build orientation, 3PB, tensile, and Iosipescu shear test specimens were printed with four different build orientations (on edge 0°,on edge 45°, on edge 90°, and flat) and three different raster angles (0°,45°, and 90°) all using parallel deposited filaments (Figure 1). Conducting tensile and Iosipescu shear testing on the printed specimen results in the calculation of all engineering constants of the RVE (detailed in Sections 3.1 and 3.5) defined for 3D printed parts when parallel filaments are used. Of course, the inter-laminar shear modulus (G₂₃) needs to be calculated. Therefore, short-beam shear test specimen with 90° raster angle was also printed and tested. In order to examine the effect of infill density, 3PB and tensile test specimens with two infill densities of 50% and 100% with the partial infill patterns of rectilinear, where the filaments are oriented at (0°/90°), were also printed. The summary of printing patterns and orientation for different types of test specimen are listed in Table 2. For the on-edge samples at 45° and 90°, a support structure using polyvinyl alcohol (PVA) provided by Ultimaker (PVA Natural, Standard PVA, 2.85 mm/750 gram) was used to ensure the geometry was maintained. To remove the PVA support structures from vertically 3D printed samples, cold water immersion was used. The 3D printed samples were then dried using hot air at 60°C for a few seconds and allowed to cool to ambient temperature before mechanical testing. Following the recommendation of the ASTM standards that were mentioned above, for each case in Table 2, five specimens were tested. In terms of failure location and depending on the failure modes (i.e., interlayer and intra-layer fracture), for each case, most specimens failed within the gauge length; however, occasionally, some samples failed outside the gauge length. In these cases, the test specimens were 3D printed anew, and mechanical tests were repeated until a successful result was produced.

Table 1 3D printing process parameters used to produce the test specimens

Figure 1

a Schematic view of 3D FFF printer, where the model is built layer by layer. b Schematic of the orientations of the specimens used in this investigation for tension, c shear, d 3PB test specimen, and e raster angle

Table 2 3D printing patterns and densities for mechanical testing

2.2 FE microstructural model of bending, shear, and tensile test samples

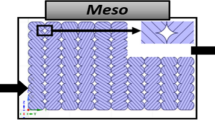
In the present study, FE explicit microstructural simulation is carried out for FFF-based 3D printed specimens using the FE package ANSYS. The isotropic properties of PLA, i.e., E=3500 MPa and ν=0.35 determined by Bollard style tensile grips [42, 43], were used as input for the FE models. Given the internal microstructure and infill patterns, models of 3PB, Iosipescu, short-beam shear, and tensile specimens were created in the design modeler tool of ANSYS. The specimens were modeled with different build orientations and raster angles described earlier in Section 2.1 all using parallel fibers. Details of build orientation and raster angle arrangements are schematically shown in Figure 2. Two infill densities of 50% and 100% for the partial infill patterns of rectilinear design where the filaments are oriented at (0°/90°) were also analyzed by FE (Figure 3). To replicate the bonding between filaments and layers due to compression by the nozzle (“squish”), instead of using the circular cross-section of filaments, they are approximated as a rounded rectangular cross-section with a certain small amount of overlap between the adjacent fibers. This is due to the diffusion of two raster layers at the interface during solidification. The shape of individual filaments and the overlap region observed under microscope can be clearly seen in Figure 4. Using a calibrated light microscope, the height and width of the filament (h and w) are measured as 0.2 mm and 0.4 mm. These measurements were used to generate a more realistic geometry model for FE of the microstructure in the FFF test specimens. To construct the full model of all mechanical test specimens with the infill structures, first the cross-section of filament is created using the dimensions obtained from the microscopic analysis (Figure 4) and then patterns schematically shown in Figure 2 and 3 are generated to prepare a rectangular model. Finally, the model is trimmed as per the exact dimension of the bending, shear, and tensile test specimens.

Figure 2

Details of layer orientation: a 90°; b 45°; c 0° raster angles for horizontally printed and d upright; e 45 and f 0° build orientation for vertically printed bending, shear, and tensile specimens. (The width and height of each filament are set to 0.4mm and 0.2 mm respectively based on the optical microscopic image of cross section of raster layers showing the shape of individual filaments)

Figure 3

Details of microstructures for the infill densities of 50% and 100% using the rectilinear infill pattern of 0°/90°. (The width and height of each filament are set to 0.4mm and 0.2 mm respectively based on the optical microscopic image of cross section of raster layers showing the shape of individual filaments)

Figure 4

Light microscopic image of a cross section of raster layers showing the shape of individual filaments after deposition where w and h stands for the width and height of filament

2.3 Macro scale FE modeling of 3D printed test samples based on homogenization approach

The macro scale FE model characterizes the design of bending, shear, and tensile test specimens using orthotropic properties of RVE for different printing process parameters. The FE model incorporates the boundary conditions with the internal lay-up of RVE. In the first stage of FE modeling of the bending, tensile, and shear test, a design modeling tool is used to create a shell model of the test specimen. The model integrates the geometry of test specimens according to the standard methods described earlier. The Surface function is used to generate a thin surface then it is transferred into the ANSYS Composite Processor (ACP) where effective engineering constants of the RVE, stacking sequences (i.e., infill patterns, build orientation, and raster angle), and thicknesses are all defined. Figure 5 shows the FE mesh and the boundary conditions imposed on the FE model of tensile, shear, and bending test coupons. In the case of FE model of 3PB, the contact between support/loading rollers and the sample was considered frictional (friction coefficient of 0.2). A mesh sensitivity study was also conducted and the convergence criterion (i.e., stabilization of stress) is met at the mesh density used. To provide input data (i.e., orthotropic engineering constants of the RVE) for the FE model of 3D printed samples in bending, tension, and shear, initially, FE analysis of RVE using the homogenization method was conducted.

Figure 5

FE mesh of a tensile, Iosipescu shear, and 3PB test specimen and optimization of boundary condition

The RVEs of 3D printed specimens with the infill patterns of parallel filaments as well as rectilinear filaments (0°/90°) with two infill densities of 50% and 100% are shown in Figure 6. These are taken from the microstructure of the 3D printed parts as seen in Figure 2 and 3. In this work, four-node tetrahedral elements in ANSYS were used to mesh the micro models of the RVE and then homogenization is done using the micro mechanics plugin in ANSYS (Material Designer). To avoid the mesh dependency in the RVE, smaller elements were used. The micro models of the RVE shown in Figure 6 is subjected to six different strains (Figure 7) applied individually using the periodic boundary condition (detailed in the following sections). Therefore, effective orthotropic engineering constants of RVE which are subsequently used as the input data for the FE simulation of bending, tensile, and shear testing are obtained. It must be noted that in this study, in both FE homogenization and explicit microstructural modeling techniques, only the elastic response of 3D printed mechanical test specimens are simulated, and viscoelastic and plastic behavior of PLA materials were not taken into account in the constitutive material behavior.

Figure 6

The RVE of the 3D printed samples, a parallel filaments, b, c filaments deposited in alternating layers of 0° and 90° at the infill density of 100% and 50%

Figure 7

State of pure uniaxial and shear strains; (a) longitudinal strain mode; (b, c) transverse strain modes; (d, e, f) shear strain modes in XY, YZ, XZ planes respectively

2.3.1 Constitutive material behavior of 3D printed specimens

To account for the material behavior in the FE stress analysis, constitutive behavior of horizontally and vertically printed bending, tensile, and shear samples are evaluated in this study. The nine elastic constants in orthotropic constitutive equations are as follows: three Young’s moduli (E_x, E_y, and E_z), three Poisson’s ratios ( v_xy, v_yz, and v_xz) and three shear moduli (G_xy, G_yz, and G_xz). The stress-strain relation for an orthotropic material is defined as:

$$ \left\{\varepsilon \right\}=\left[s\right]\left\{\sigma \right\} $$

(1)

where S is the compliance matrix:

$$ \left[\begin{array}{cccccc}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${E}_x$}\right.& -\raisebox{1ex}{${v}_{xy}$}\!\left/ \!\raisebox{-1ex}{${E}_y$}\right.& -\raisebox{1ex}{${v}_{xz}$}\!\left/ \!\raisebox{-1ex}{${E}_z$}\right.& 0& 0& 0\\ {}-\raisebox{1ex}{${v}_{yx}$}\!\left/ \!\raisebox{-1ex}{${E}_x$}\right.& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${E}_y$}\right.& -\raisebox{1ex}{${v}_{zy}$}\!\left/ \!\raisebox{-1ex}{${E}_z$}\right.& 0& 0& 0\\ {}-\raisebox{1ex}{${v}_{zx}$}\!\left/ \!\raisebox{-1ex}{${E}_x$}\right.& -\raisebox{1ex}{${v}_{yz}$}\!\left/ \!\raisebox{-1ex}{${E}_y$}\right.& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${E}_z$}\right.& 0& 0& 0\\ {}0& 0& 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2{G}_{yz}$}\right.& 0& 0\\ {}0& 0& 0& 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2{G}_{xz}$}\right.& 0\\ {}0& 0& 0& 0& 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2{G}_{xy}$}\right.\end{array}\right] $$

(2)

Therefore, to consider the material behavior in the FE stress analysis of the 3D printed specimens, the coefficients of the constitutive matrix (stiffness values) need to be determined. This is done in this study using the numerical homogenization technique.

2.3.2 Homogenization

The method of prediction of the constitutive matrix (effective orthotropic properties) of materials based on the properties of constituent and geometrical aspects of the microstructure is called homogenization. In 3D printing of specimens, these properties are calculated from the properties of the raw PLA used for printing, where two constants are required, Young’s modulus and Poisson’s ratio. A small volume of material with repeating unit cells which is called an RVE (Figure 6) is considered for the numerical homogenization analysis. In the homogenization technique, given the assumption that the stored strain energy in the heterogeneous volume of the RVE (V_rve) is the same as a homogeneous RVE, the effective properties of heterogeneous materials can be obtained. The stored strain energy (E) in the heterogeneous RVE of volume (V_rve) is calculated as

$$ {E}^{\ast }=0.5\int {\upsigma}_{ij}{\upvarepsilon}_{ij}\mathrm{dV} $$

(3)

Also, the strain energy of an equivalent homogeneous RVE is defined as:

$$ E=0.5\times \overline{\sigma_{ij}}\times \overline{\varepsilon_{ij}} \times {V}_{\mathrm{rve}} $$

(4)

where $\overline{\sigma_{ij}}$ and $\overline{\varepsilon_{ij}}$ are calculated by averaging the local stress and strain fields over the RVE’s volume (V_RVE)

$$ \overline{\sigma_{ij}}=\frac{1}{V_{rve}}\int {\sigma}_{ij} dV,\overline{\varepsilon_{ij}}=\frac{1}{V_{rve}}\int {\varepsilon}_{ij} dV. $$

(5)

By defining periodic boundary conditions on the RVE and substituting Eq. 1 into Eq. 4, the components of compliance matrix (orthotropic elastic constants) in Eq. 2 can be calculated. This is done when the micro-model of the RVE is loaded in accordance with the boundary conditions representing uniaxial strain (a, b, and c) and shear strain (d, e, and f) states of the RVE positioned in the origin of the coordinate system (Figure 7). For each state of strain in Figure 7, the volume average stress, strain, and total strain energy are obtained from the FE results to construct the numerical prediction of orthotropic elastic properties. More details of expressions used to calculate the elements of compliance matrix is available in the literature [33, 44].

2.3.3 Generating periodic boundary conditions

In the numerical homogenization method, uniform strains are applied to the RVE model to compute the effective elastic properties. By applying these strains in independent sets, specific elastic properties are calculated for each set. The RVE is part of a periodic material; therefore, before and after imposing the strains, the periodicity of the RVE with the surrounding material needs to be simulated in the FE software. This is achieved by imposing node-to-node periodic boundary conditions to the deformed boundary surfaces of the RVE. In FE software, this is done either by coupling the degrees of freedom (DoF) of the corresponding nodes in the corresponding directions or by using a constraint equation to define the specific relationship between the corresponding nodes in the boundary. Given the definition of top/bottom, left/right and back/front surfaces, corners, and edges in the RVE, sets of Eq. 6 and Eq. 7 between the two opposite nodes in the RVE are defined. The common nodes on edges and corners of the RVE were also defined once.

• For the measurement of elastic modulus (E_x):

$$ {\displaystyle \begin{array}{c}X\ \mathrm{at}\ \mathrm{front}\ \mathrm{nodes}-X\ \mathrm{at}\ \mathrm{back}\ \mathrm{nodes}=\varDelta \\ {}X\ \mathrm{at}\ \mathrm{top},\mathrm{left}\ \mathrm{nodes}-X\ \mathrm{at}\ \mathrm{bottom},\mathrm{right}\ \mathrm{nodes}=0\\ {}Y\ \mathrm{at}\ \mathrm{top},\mathrm{front},\mathrm{left}\ \mathrm{nodes}-Y\ \mathrm{at}\ \mathrm{back},\mathrm{bottom},\mathrm{right}\ \mathrm{nodes}=0\\ {}Z\ \mathrm{at}\ \mathrm{front},\mathrm{top},\mathrm{left}\ \mathrm{nodes}-Y\ \mathrm{at}\ \mathrm{back},\mathrm{bottom},\mathrm{right}\ \mathrm{nodes}=0\end{array}} $$

(6)

• For the measurement of shear modulus (G_xy):

$$ {\displaystyle \begin{array}{c}X\ \mathrm{at}\ \mathrm{front},\mathrm{left}\ \mathrm{nodes}-X\ \mathrm{at}\ \mathrm{back},\mathrm{right}\ \mathrm{nodes}=0\\ {}Y\ \mathrm{at}\ \mathrm{front}\ \mathrm{nodes}-Y\ \mathrm{at}\ \mathrm{back}\ \mathrm{nodes}=\varDelta \\ {}X\ \mathrm{at}\ \mathrm{top}\ \mathrm{nodes}-X\ \mathrm{at}\ \mathrm{bottom}\ \mathrm{nodes}=\varDelta \\ {}Y\ \mathrm{at}\ \mathrm{top},\mathrm{left}\ \mathrm{nodes}-Y\ \mathrm{at}\ \mathrm{bottom},\mathrm{right}\ \mathrm{nodes}=0\\ {}Z\ \mathrm{at}\ \mathrm{front},\mathrm{top},\mathrm{left}\ \mathrm{nodes}-Y\ \mathrm{at}\ \mathrm{back},\mathrm{bottom},\mathrm{right}\ \mathrm{nodes}=0\end{array}} $$

(7)

where X, Y, and Z are the components of displacements along the X, Y, and Z axes. ∆ is the applied displacement.

2.3.4 Calculating Young’s modulus, Poisson’s ratio, and shear modulus

By applying a displacement on the surfaces of the RVE, boundary nodal forces are created at the affected boundary surfaces. Therefore, dividing the sum of the boundary nodal forces at the affected boundary nodes (reaction force as denoted by F in Eq. 8 and Eq. 9) by the area of affected surface yields the stress value corresponding to the applied strain (applied displacement divided by the length of the RVE); therefore, Young’s modulus as well as shear modulus are calculated as shown in Eq. 8, Eq. 9, and Fig. 8. Correspondingly by calculating the transverse strain and dividing it by the applied strain, Poisson’s ratio is also estimated.

$$ {E}_{11}=\frac{\sigma }{\varepsilon }=\frac{\frac{\varSigma {F}^{\ast }}{H\times W}}{\frac{\varDelta L}{L}} $$

(8)

where F^∗ is the sum of the front surface nodal forces along the x axis:

$$ {G}_{12}=\frac{G}{\varepsilon_{12}}=\frac{\frac{\varSigma {F}^{\ast \ast }}{L\times W}}{\frac{\varDelta 1}{H}+\frac{\varDelta 2}{L}} $$

(9)

where Fe^∗∗ is the sum of the top surface nodal forces along the x axis:

$$ {v}_{12}=\frac{\frac{\varDelta H}{H}}{\frac{\varDelta L}{L}},{v}_{13}=\frac{\frac{\varDelta W}{W}}{\frac{\varDelta L}{L}} $$

(10)

Figure 8

Prediction of Young’s modulus, Poisson’s ratio, and shear modulus when the RVE is subjected to displacement in x direction

3 Results and discussion

In this study, horizontally and vertically 3D printed structures are considered for material modeling to compute their orthotropic engineering constants using homogenization technique. The effect of build and raster orientation of the respective vertical and horizontal structures on the bending, tensile, and Iosipescu properties is discussed. In addition, the effect of infill densities with the rectilinear infill pattern on the tensile and bending properties is discussed. This is done by calculating the effective orthotropic properties of RVEs and then using the properties as an input for the FE homogenization simulation of bending, tensile, and shear tests. The results of FE homogenization are finally compared with FE explicit microstructural simulations and experiment.

3.1 RVE with parallel filaments

The FE model of an RVE (with parallel filaments) using the periodic meshing is shown in Figure 9, then the FE simulation for homogenization of the material is conducted and therefore the unknown elements of the orthotropic constitutive matrix are calculated, as explained in Sections 2.3.2, 2.3.3, and 2.3.4. The elements of the elastic moduli of the orthotropic material are calculated from the constitutive matrix using Equation 2 and the results are provided in Table 3.

Figure 9

FE model of the RVE for a 3D printed part with parallel filaments

Table 3 The elastic moduli of the RVE

3.2 RVE with rectilinear pattern

This section shows the results of numerical homogenization of the 3D printed structures using the following process parameter rectilinear infill patterns (stacking sequence of the layers with defined raster angle in horizontal part is (0°/90°)). Two different infill densities of 50% and 100% are investigated. The FE model of the RVEs using the periodic meshing is shown in Figure 10, then the FE simulation for homogenization of the material is conducted and therefore the elements of elastic moduli for the orthotropic material are calculated (Table 3).

Figure 10

FE model of RVEs for 3D printed parts with rectilinear infill patterns. a Infill densities of 50% and b 100%

3.3 Numerical versus experimental 3PB and shear testing

Using the orthotropic engineering constants of RVE (Table 3 and Table 4) as an input data for the FE model of test samples as described in Section 2.3, 3D printed bending, tensile, and shear tests are simulated. Representative DIC and FE calculated bending and shear strain fields are depicted in Figure 11 indicating that there is a good agreement between experimentally and numerically calculated strain distribution. However, the effect of raster angle, build orientation, and infill density on the stress localization in FE homogenization cannot be studied. Although changing the raster angle, build orientation, and infill density results in different strain values, the strain distribution maps in FE homogenization technique remain unchanged. Figure 12 and 13 show the effect of raster angle, build orientation, and infill density on experimentally and numerically generated bending and shear properties.

Table 4 Elastic moduli of the RVEs for two infill densities of 50% and 100%—infill patterns of rectilinear with stacking sequence of (0°/90°)

Figure 11

Experimental (DIC) and FE (homogenization) calculated strain fields of 3D printed a bending specimen with 0° raster angle at the load of 75 N, b Iosipescu shear specimen with 0° raster angle at the stress value of 5 MPa, and c ILS test specimen with 90° raster angle at the stress value of 5 MPa

Figure 12

Effect of a, b raster angle; c, d build orientation; and e, f infill density on numerically calculated 3PB load deflection (elastic regime) and experimentally generated 3PB load deflection plots (representative 3PB load-deflection plots)

Figure 13

Effect of a, b raster angle; c, d build orientation; and e, f infill density on numerically calculated shear stress strain (elastic regime) and experimentally generated shear stress strain plots (representative shear stress-strain plots)

As can be seen from these figures, when the build orientation and raster angles increase from 0° to 90°, the experimentally calculated flexural modulus reduces by 31.2% and 32.3%, while the FE calculated flexural modulus reduces by 25.4% and 25.7% respectively. In addition, when the build orientation and raster angles increase from 0° to 45°, the experimentally calculated in plane shear modulus increases by 25.4% and 23.6% while the FE calculated in plane shear modulus increases by 19.8% and 18.7%. This shows that the FE model can predict reasonably well the effect of build/raster angle on the bending and shear modulus of 3D printed parts when using parallel filaments.

The difference between FE and experimental flexural and shear modulus when changing build/raster orientation and infill density are shown in Figure 14 a and b. As it can be seen from this figure, the difference between experimental and numerical flexural modulus is less than 10% when build and raster orientation are 0°; however, when the orientation increases to 45° and 90°, the difference increases by about 11% and 14% respectively. Conversely, the difference between experimental and numerical shear modulus decreases from 11 to 7% when the raster angle/build orientation increases from 0° to 45°. The reason for variation in the numerically and experimentally calculated elastic moduli is that in the FE analysis, it is assumed that the bonding between adjacent filaments is perfect; however, this is not the case for the real 3D printed parts. In Section 3.3.1, it is shown by FE explicit microstructural modeling that when performing off-axis mechanical testing (bending and shear), the bonding between filaments is a controlling factor in mechanical properties. As the bonds in FE model are assumed to be perfect, the difference between FE and experiment becomes more highlighted when build/raster orientation changes.

Figure 14

Difference between FE and experimentally determined flexural modulus and shear modulus. a Effect of build/raster orientation on flexural modulus, b effect of build/raster orientation on shear modulus, and c effect of infill density on flexural and shear modulus

While the difference between FE and experimentally determined bending and shear modulus for 3D printed samples with 100% density is around 9% (Figure 14c), the difference becomes significant when the infill density is 50%. In Figure 14 c, it is shown that even the FE model underestimates the bending and shear modulus when the infill density is 50%. In addition, when infill density increases from 50 to 100%, the experimentally determined flexural modulus and shear modulus increase by 2.65 and 61.6 times, while FE calculated flexural and shear modulus increase by 4.4 and 96.6 times, indicating that infill density has significant impact on the mechanical properties of 3D printed parts. The main reason for the difference between FE and experimental results when using partial infill patterns is the gap between filaments in the developed FE model of the RVE in Figure 10 a, while this gap does not exist in the 3D printed parts. Nevertheless, apart from the partial infill patterns (i.e., infill density of 50%), the present FE analysis is an alternative to the experimental and can provide accurate results compared with that experimental work.

3.3.1 FE microstructural analysis of 3PB and shear testing

As discussed earlier, the effect of raster angle, build orientation, and infill density on the stress localization in FE homogenization calculated strain fields cannot be studied. In order to demonstrate the effect of these parameters, and also to predict the local failure mechanisms and to investigate important features of micromechanics such as the effect of raster angle and build orientation on stress localization, FE microstructural simulation of bending and shear tests was conducted in this work. The stress contours of bending and shear test specimens and the effect of build orientation and raster angles are shown in Figure 15, 16, 17, 18. In addition, FE microstructural simulation of the bending test for the 3D printed samples with two infill densities of 50% and 100% has been carried out (Figure 19). As can been seen in all these figures, the maximum stress in all cases occurs at the interface of the PLA filaments. Therefore, the weakest section in the microstructure of 3D printed parts is the interface between deposited filaments or layers and this is more susceptible to crack initiation during deformation. As a result, de-bonding between PLA filaments can occur during the bending and shear loads, finally leading to the failure of the FFF-based 3D printed parts. In addition, in Figures 15, 16, 17, 18 and 19, the corresponding load-deflection and stress-strain behavior (and therefore bending and shear modulus in the elastic regimes) are shown. Comparing the bending and shear modulus obtained by FE microstructural simulation with modulus obtained by FE homogenization (detailed in Figure 12 and 13) shows that the two FE methods agree well with each other.

Figure 15

FE calculated stress fields (longitudinal stress) during 3PB test simulation on horizontally 3D printed samples where a raster angle is 0°, b raster angle is 45°, and c raster angle is 90°. d Effect of raster angle on FE calculated flexural stress-strain plots

Figure 16

FE calculated stress fields (longitudinal stress) during 3PB test simulation on vertically 3D printed samples where a build orientation is 0°, b build orientation is 45°, and c build orientation is 90°. d Effect of build orientation on FE calculated flexural stress-strain plots

Figure 17

Effect of build orientation on FE calculated shear stress fields. a 0°, b 45°, c 90°. d Effect of build orientation on FE calculated shear stress-strain plots

Figure 18

Effect of raster angle on FE calculated shear stress fields. a 0°, b 45°, c 90°. d Effect of raster angle on FE calculated shear stress-strain plots

Figure 19

FE calculated stress fields (longitudinal stress) during 3PB test simulation on 3D printed samples with the infill pattern of rectilinear and infill densities of a 100%, and b 50%. c Effect of infill density on FE calculated flexural stress strain plots

3.4 Numerical versus experimental tensile testing

Unlike bending or shear test, the effect of raster and build orientation on the experimentally generated localized tensile strain fields can be observed and analyzed. In previous work [37], the effect of build orientation on DIC-generated tensile strain fields has been investigated. In the present study, when raster angle changes from 0° to 90°, DIC computed tensile strain fields are shown in Figure 20. The highest localized strains in this figure indicates the effect of defects produced during the printing process. When the raster angle is 45° or 90°, the highest localized strain occurs at the interface between filaments which are oriented in the 45° and 90° planes. This is verified by the results of FE explicit microstructural analysis in Section 3.4.1 (Figure 24) where the maximum stress/strain occurs at the interface of PLA filaments indicating that the interface is more susceptible to crack initiation during the deformation, and therefore, de-bonding between PLA filaments can be predicted because of the tensile loads. Comparison of the fracture surfaces shows that the failure mode changes as a function of raster angle. Failure from 0° to 90° orientation changes from ductile to brittle; the transition in behavior from ductile to brittle fracture is mainly due to the layer deposition direction. In 0° raster angle, the layer deposition direction was parallel to the specimen axis and the load was applied parallel to the layers; therefore, ductile fracture is observed with significant plastic deformation. As the raster angle increases, the specimens display an intermediate brittle-ductile fracture behavior. Noticeably, when the raster angle increases (≥ 45°), the specimen demonstrates the transition to brittle failure, with little plastic deformation. The 90° raster angle fails by brittle fracture due to inter-layer fusion bond failure as the load is applied perpendicular to their layers; the stress strain curve exhibits a linear trend followed by sudden failure.

Figure 20

DIC strain distribution map in terms of longitudinal strains prior to the fracture point for different raster angles of 3D FDM printed tensile specimen of a 0°, e 45°, and f 90°. DIC maps were captured at the overall stress of 50 MPa, 32 MPa, and 22 MPa when the raster angles are 0°, 45°, and 90° respectively

Using the orthotropic engineering constants of the RVE (Table 3 and Table 4) as input data for the FE model of the samples, the tensile test is simulated. Representative FE (homogenization) calculated tensile strain fields are depicted in Figure 21; however, the effect of raster angle, build orientation, and infill density on the localized stress in FE homogenization cannot be studied. This means that although changing the raster angle, build orientation, and infill density result in different strain values and strain distribution maps in FE, the calculated strain fields remain unchanged. Figure 22 shows the effect of raster angle, build orientation, and infill density on experimentally and numerically generated tensile properties in terms of their respective stress-strain plots. As can be seen from this figure, by comparing FE and experimentally determined tensile moduli when build/raster orientation and infill density change, a similar discussion to the effect of processing parameters on bending properties (Section 3.3) can be made when analyzing the tensile data. This means that apart from the partial infill patterns (infill density of 50%), the FE model can predict well the effect of build/raster angle on the tensile modulus of 3D printed parts. The variation between the numerically and experimentally calculated elastic moduli is due to the assumption of a perfect bond between adjacent deposited filaments in the FE model, while this is not the case for 3D printed parts. In Section 3.4.1, it is shown by FE explicit microstructural modeling that when conducting off-axis tensile testing, the bond between filaments is a determinant factor in tensile properties. As the bonds in FE model are assumed to be perfect, the difference between FE and experiment becomes more highlighted when build/raster orientation changes.

Figure 21

FE (homogenization) calculated tensile stress distribution for horizontally (raster angle of 0°) 3D printed parts

Figure 22

Effect of a, b raster angle; c, d build orientation; and c infill density on numerically calculated tensile stress-strain plots (elastic regime) and experimentally generated tensile stress-strain curves (representative tensile stress/strain plots)

3.4.1 FE microstructural analysis of tensile testing

To investigate the effect of raster angle/build orientation and infill density on the stress localization, FE microstructural simulation of tensile tests was conducted in this work. In Figure 23 and Figure 24, it is shown that the maximum stress occurs at the interface of PLA filaments. This indicates that the interface is more susceptible to crack initiation during the deformation, and therefore, debonding between PLA filaments can occur due to the tensile loads. The localized stress contours of tensile test specimens and the effect of infill densities are shown in Figure 25. As can be seen in this figure, when samples with 50% infill density are subjected to tensile loads, most loads are sustained by the longitudinal PLA filaments and in the interface between filaments stress transfer can also be observed. In the case of 100% infill density, although most tensile loads are taken by longitudinal filaments, localized stress between filaments are greater in terms of magnitude; therefore, failure (de-bonding between filaments) is predicted at the interface.

Figure 23

Effect of build orientation on FE calculated tensile stress fields. a 0°, b 45°, c 90°. d Effect of build orientation on FE calculated tensile stress strain plots

Figure 24

Effect of raster angle on FE calculated tensile stress fields. a 0°, b 45°, c 90°. d Effect of raster angle on FE calculated tensile stress strain plots

Figure 25

FE microstructural simulation of 3D printed tensile sample with infill density of a 50% and b 100%. c Effect of infill density on FE calculated tensile stress-strain plots

3.5 Verification of RVE properties

One of the main objectives in the present study is to validate the effective orthotropic engineering constants of the RVE (Figure 9) obtained by FE homogenization against the experimentally determined values. Table 5 shows the method of tensile and shear testing used in this work to experimentally determine the elements of the elastic moduli and validate the properties of the RVE in Table 3. In Table 6, numerically and experimentally determined elements of the elastic moduli are compared. While for most of the elements less than 10% difference between FE and experimental results are observed, a bigger difference (around 1315%) for the transverse, through the thickness modulus and inter-laminar shear modulus (i.e. E₂, E₃ and G₂₃), is seen, mainly due to the effect of bonding at the interface between deposited filaments. As was explained in Sections 3.3.1 and 3.4.1, the bond between filaments at the interfaces are assumed to be perfect in the FE model, while this is not true in the 3D printed parts subjected to mechanical testing. In addition, the elements of the elastic moduli obtained from FE microstructural analysis agree well (less than 2% difference) with the elements of elastic moduli obtained from FE homogenization, indicating that the results of FE homogenization is validated against the microstructural simulation as well.

Table 5 Mechanical testing method and the position/direction of 3D printed specimens to determine and validate the elements of moduli obtained by FE homogenization

Table 6 Difference between FE and experimentally determined elastic moduli components

3.6 Industrial applications

The validation of FEA results against experimental data in the context of additive manufacturing (3D printing) obtained in this study is fundamental in automotive, aerospace, and biomedical industries where the optimal material distribution in a certain volume exposed to mechanical constraints can be determined resulting in significant reduction in the cost and time of manufacturing process of load-bearing components and structures. This can be obtained through the use of FEM techniques such as ANSYS space-claim design tools where the boundary conditions, types of materials, and 3D printing process parameters such as internal microstructures, infill densities, and layer height can be integrated and optimized. In particular, the automotive industry seeks to solve challenges in cost and time to manufacture with material savings in mass production. In fact, a small drop (a few grams) per automobile, on an assembly of several thousand units, results in considerable material savings. The aerospace industry is certainly another area very keen in FEA analysis of 3D printing by the means of topology optimization to reduce weight and costs. A lighter aeroplane uses less energy, which in turn causes substantial savings for an airline company. Finally, the medical industry is very interested in designing methodologies, especially to produce bespoke implants where FEA tools in 3D printing such as lattice optimization tools allow it to replicate the density of bone, while decreasing the component weight. Many implants incorporate lattice structures and are as robust as those conventionally designed and manufactured.

4 Conclusion

The constitutive material behavior of FFF-based 3D printed parts depends on processing parameters such as build orientation, raster angles, infill patterns, and densities. Although an isotropic material such as PLA is used for 3D printing, the structure, and the mechanical behavior of the part is orthotropic. In the present study, the computation of the effective orthotropic properties of printed parts using the numerical homogenization method based on a multi scale approach was presented. The technique was used to predict the influence of printing process parameters on the elastic response of 3D printed mechanical test samples. The analysis of micro-mechanic models of an RVE is used to calculate the effective elastic constants which were subsequently used as an input for the creation of macro scale FE models of 3PB, tensile, and shear samples. Finally, the results obtained by homogenization technique were validated against experimental as well as FE explicit microstructural models. Some key conclusions are as follows:

• Although FE explicit microstructural simulation is computationally much more expensive compared to the multi scale numerical homogenization technique, it is useful to identify the localized stress at the interfaces between the adjacent fibers and layers and therefore to predict the types of failure modes in FFF-based 3D printed parts.

• Comparing the results of FE homogenization and explicit microstructural methods with the experimental results for different printing orientations shows that both FE methodologies used in this work can predict the effect of printing orientation on the elastic properties.

• Both FE and experimental results show that infill density is the most determinant factor of the 3D printed parts as the change in the infill density significantly affects their mechanical properties.

• Although the FE methodologies developed in this work can predict well the elastic properties of 3D printed parts with 100% infill density, for the partial infill pattern, the FE models need to be improved further.

• The numerical methods developed in this study showed the ability to predict the elastic properties of 3D printed structures. This can result in a significant reduction in the number of mechanical tests which are usually needed for evaluating the behavior of 3D printed parts; as a result, significant time and cost can be saved using the FE approach in this study.

• The approach used in this work also enables the designer to conduct faster iterative analysis and choose optimized printing process parameters based on FE in order to produce high-quality FFF-based 3D printed parts.