Skip to main content
SpringerLink
Log in

A new mathematical model for predicting the diameter expansion of flat ring in radial–axial ring rolling

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

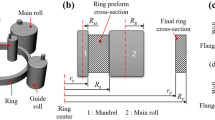
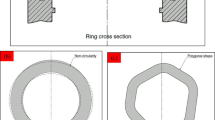
An accurate prediction for the diameter expansion is quite essential for the ring rolling with large diameter since it determines the compatibility between the work rolls and the deformed ring in kinematics, so that the rolling stability and the final forming quality of the ring are influenced. A new mathematical model for predicting the diameter expansion of the flat ring in the radial–axial rolling process has been proposed, in which the variation of cross section, the particularity of initial rolling phase, and the effect of slip are all taken into consideration. Based on the proposed mathematical model, a 3D-FEM model for the radial–axial ring rolling process has been developed, and the corresponding experimentation has also been carried out. The diameter expansion in the simulation shows a good agreement with that in the experimentation. The forming quality comparison concerning the circularity, coaxiality, and tilting of the rolled ring has been executed between the former and new proposed method. The result indicates that the new mathematical method is very helpful to control the forming stability and hence improve the ring rolling quality significantly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Mamalis AG, Hawkyard JB, Johnson W (1976) Spread and flow patterns in ring rolling. Int J Mech Sci 18:11–16

    Article  MATH  Google Scholar 

  2. Johnson W, Needham G (1968) Experiments on ring rolling. Int J Mech Sci 10:95–113

    Article  Google Scholar 

  3. Mamalis AG, Hawkyard JB, Johnson W (1976) On the pressure distribution between stock and rolls in ring rolling. J Mater Eng Sci 18:184–195

    Google Scholar 

  4. Allwood JM, Kopp R, Michels D, Music O, Öztop M, Stanistreet TF, Tekkaya AE, Tiedemman I (2005) The technical and commercial potential of an incremental ring rolling process. CIRP Ann-Manuf Techn 54:233–236

    Article  Google Scholar 

  5. Lugora CF, Bramiley AN (1987) Analysis of spread in ring rolling. Int J Mech Sci 29:149–157

    Article  MATH  Google Scholar 

  6. Mamalis AG, Hawkyard JB, Johnson W (1976) Pressure distribution, roll force and torque in cold ring rolling. J Mech Eng Sci 18:196–209

    Article  Google Scholar 

  7. Hawarkyard JB, Johnson W, Kirkland J, Appleton E (1973) Analyses for roll force and torque in ring rolling with some supporting experiments. Int J Mech Sci 15:873–893

    Article  Google Scholar 

  8. Qan DS, Hua L, Pan LB (2009) Research on gripping conditions in profile ring rolling of raceway groove. J Mater Process Tech 209:2794–2802

    Article  Google Scholar 

  9. Hua L, Zuo ZJ, Lan J (2007) Research on following motion rule of guide roller in cold rolling groove ball ring. J Mate Process Tech 187–188:743–746

    Article  Google Scholar 

  10. Davey K, Ward MJ (2003) An ALE approach for finite element ring-rolling simulation of profiled rings. Mater Process Tech 139:559–566

    Article  Google Scholar 

  11. Davey K, Ward MJ (2002) A practical method for finite element ring rolling simulation using the ALE flow formulation. Int J Mech Sci 44:165–190

    Article  MATH  Google Scholar 

  12. Youngsoo Y, Youngsoo K, Nasoo K, Jongchan L (2003) Prediction of spread, pressure distribution and roll force in ring rolling process using rigid-plastic finite element method. J Mate Process Tech 140:478–486

    Article  Google Scholar 

  13. Joun MS, Chung JH, Shivpuri R (1998) An axisymmetric forging approach to preform design in ring rolling using a rigid-viscoplastic finite element method. Int J Mach Tool Manu 38:1183–1191

    Article  Google Scholar 

  14. Ranatunga V, Gunasekera JS, Vaze SP, Souza UD (2004) Three-dimensional UBET simulation tool for seamless ring rolling of complex profiles. J Manu Process 6:179–186

    Article  Google Scholar 

  15. Moon HK, Lee MC, Joun MS (2008) Predicting polygonal-shaped defects during hot ring rolling using a rigid-viscoplastic finite element method. Int J Mech Sci 50:306–314

    Article  Google Scholar 

  16. Anjami N, Basti A (2010) Investigation of rolls size effects on hot ring rolling process by coupled thermo-mechanical 3D-FEA. J Mater Process Tech 210:1364–1377

    Article  Google Scholar 

  17. Forouzan MR, Salimi M, Gadala MS, Aljawi AA (2003) Guide roll simulation in FE analysis of ring rolling. J Mater Process Tech 142:213–223

    Article  Google Scholar 

  18. Li LY, Yang H, Guo LG, Sun ZC (2008) A control method of guide rolls in 3D-FE simulation of ring rolling. J Mater Process Tech 205:99–110

    Article  Google Scholar 

  19. Guo LG, Yang H (2008) Key technologies for 3D-FE modeling of radial–axial ring rolling process. Mater Sci Forum 575–578:367–372

    Article  Google Scholar 

  20. Guo LG, Yang H (2004) Simulation for guide roll in 3D-FE analysis of cold ring-rolling. Mater Sci Forum 471–472:760–764

    Article  Google Scholar 

  21. Liu D, Wan ZY, Fu MJ (2008) Kinematics analysis in radial–axial rolling. Chin J Mech Eng 19:466–468 (in Chinese)

    Google Scholar 

  22. Hua L, Zhao ZZ (1997) The extremum parameters in ring rolling. J Mater Process Tech 69:273–276

    Article  Google Scholar 

  23. Hua L, Huang XG, Zhu CD (2001) Theory and technology of ring rolling. China Machine Press, Beijing (in Chinese)

    Google Scholar 

Download references

Acknowledgments

The authors would like to thank for the support of Ministry of Science and Technology Sino-German Cooperation Project (2010DFA51860), Natural Science Foundation Project of CQ (CSTC, 2010BB4245) and the Fundamental Research Funds for the Central Universities of China (CDJZR1013 0019).

Author information

Authors and Affiliations

  1. College of Material Science and Engineering, Chongqing University, Chongqing, 400044, China

    Wujiao Xu, Xiaobing Yang, Xiaotao Gong & Jie Zhou

Authors
  1. Wujiao Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaobing Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaotao Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jie Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaobing Yang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xu, W., Yang, X., Gong, X. et al. A new mathematical model for predicting the diameter expansion of flat ring in radial–axial ring rolling. Int J Adv Manuf Technol 60, 913–921 (2012). https://doi.org/10.1007/s00170-011-3666-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-011-3666-y

Keywords

Search

Navigation