Skip to main content

Advertisement

Springer Nature Link
Account
Menu
Find a journal Publish with us Track your research
Search
Cart
  1. Home
  2. Theoretical and Computational Fluid Dynamics
  3. Article

Diffraction of cnoidal waves by vertical cylinders in shallow water

  • Original Article
  • Open access
  • Published: 13 June 2018
  • Volume 32, pages 561–591, (2018)
  • Cite this article
Download PDF

You have full access to this open access article

Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript
Diffraction of cnoidal waves by vertical cylinders in shallow water
Download PDF
  • Masoud Hayatdavoodi  ORCID: orcid.org/0000-0003-3554-34381,
  • Douglas R. Neill2 &
  • R. Cengiz Ertekin3 

  • 909 Accesses

  • 18 Citations

  • 1 Altmetric

  • Explore all metrics

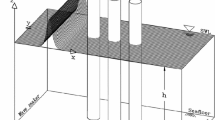
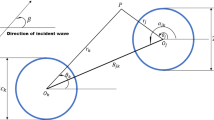
Abstract

Diffraction of nonlinear waves by single or multiple in-line vertical cylinders in shallow water is studied by use of different nonlinear, shallow-water wave theories. The fixed, in-line, vertical circular cylinders extend from the free surface to the seafloor and are located in a row parallel to the incident wave direction. The wave–structure interaction problem is studied by use of the nonlinear generalized Boussinesq equations, the Green–Naghdi shallow-water wave equations, and the linearized version of the shallow-water wave equations. The wave-induced force and moment of the Green–Naghdi and the Boussinesq equations are presented when the incoming waves are cnoidal, and the forces are compared with the experimental data when available. Results of the linearized equations are compared with the nonlinear results. It is observed that nonlinearity is very important in the calculation of the wave loads on circular cylinders in shallow water. The variation of wave loads with wave height, wavelength and the spacing between cylinders is studied. Effect of the neighboring cylinders, and the shielding effect of upwave cylinders on the wave-induced loads on downwave cylinders are discussed.

Article PDF

Download to read the full article text

Similar content being viewed by others

Wave Diffraction in a Two-Layer Fluid by the Submerged Horizontal Circular Cylindrical Pipe in Front of a Cliff as a Vertical Wall

Chapter © 2024

On solitary wave diffraction by multiple, in-line vertical cylinders

Article 16 November 2017

Diffraction of hydroelastic waves by multiple vertical circular cylinders

Article Open access 10 November 2018
Use our pre-submission checklist

Avoid common mistakes on your manuscript.

References

  1. Abul-Azm, A.G., Williams, A.N.: Approximation of second-order diffraction loads on arrays of vertical circular cylinders. J. Fluids Struct. 3, 17–36 (1989)

    Article  Google Scholar 

  2. Apelt, C., Piorewicz, J.: Laboratory studies of breaking wave forces acting on vertical cylinders in shallow water. Coast. Eng. 11(3), 263–282 (1987)

    Article  Google Scholar 

  3. Bai, W., Taylor, R.E.: Numerical simulation of fully nonlinear regular and focused wave diffraction around a vertical cylinder using domain decomposition. Appl. Ocean Res. 29, 55–71 (2007)

    Article  Google Scholar 

  4. Boussinesq, J.: Thorie de l’intumescence liquide appele onde solitaire ou de translation. Comptes Rendus Acad Sci Paris 72, 755–759 (1871)

    MATH  Google Scholar 

  5. Burden, R.L., Faires, J.D.: Numerical Analysis, 3rd edn. Prindle, Weber & Schmidt Publishers, Boston (1985)

    MATH  Google Scholar 

  6. Chakrabarti, S.K.: Wave forces on multiple vertical cylinders. J. Waterw. Port Coast. Ocean Div ASCE 104(WW3), 311–317 (1978)

    Google Scholar 

  7. Chakrabarti, S.K., Tam, W.A.: Gross and local wave loads on a large vertical cylinder—theory and experiment. In: Proceedings of Offshore Technology Conference, Houston, TX, vol. I, Paper No. OTC 1817, pp. 813–826 (1973)

  8. Chau, F.P., Taylor, R.E.: Second-order wave diffraction by a vertical cylinder. J. Fluid Mech. 240, 571–599 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  9. Demirbilek, Z., Webster, W.C.: Application of the Green–Naghdi theory of fluid sheets to shallow water wave problems. Technical Report CERC-92-11, US Army Corps of Engineers, Vicksburg, Mississippi, p. 48 (1992)

  10. Demirbilek, Z., Webster, W.C.: User’s manual and examples for GNWAVE. Technical Repoert CERC-92-13, US Army Corps of Engineers, Vicksburg, Mississippi, p. 56 (1992)

  11. Ertekin, R.C.: Soliton generation by moving disturbances in shallow water: theory, computation and experiment. PhD thesis, University of California at Berkeley, May, pp. v+352 (1984)

  12. Ertekin, R.C.: Nonlinear shallow water waves: the Green–Naghdi equations. In: Proceedings of Pacific Congress on Marine Science and Technology, PACON ’88, Honolulu, pp. OST6/42–52 (1988)

  13. Ertekin, R.C., Becker, J.M.: Nonlinear diffraction of waves by a submerged shelf in shallow water. J Offshore Mech. Arctic Eng. 120, 212–220 (1998)

    Article  Google Scholar 

  14. Ertekin, R.C., Kim, J.W.: Hydroelastic response of a floating mat-type structure in oblique, shallow-water waves. J. Ship Res. 43(4), 241–254 (1999)

    Google Scholar 

  15. Ertekin, R.C., Sundararaghavan, H.: Refraction and diffraction of nonlinear waves in coastal waters by the level I Green–Naghdi equations. In: ASME 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, American Society of Mechanical Engineers, pp. 675–684 (2003)

  16. Ertekin, R.C., Xia, D.: Hydroelastic response of a floating runway to cnoidal waves. Phys. Fluids 26(2), 027101 (2014)

    Article  Google Scholar 

  17. Ertekin, R.C., Webster, W.C., Wehausen, J.V.: Waves caused by a moving disturbance in a shallow channel of finite width. J. Fluid Mech. 169, 275–292 (1986)

    Article  MATH  Google Scholar 

  18. Ertekin, R.C., Qian, Z.M., Wehausen, J.V.: Upstream solitons and wave resistance. In: Chapter in Engineering Science, Fluid Dynamics, pp. 29–43. World Scientific, New Jersey (1990)

  19. Ertekin, R.C., Liu, Y.Z., Padmanabhan, B.: Interaction of incoming waves with a steady intake-pipe flow. J. Offshore Mech. Arctic Eng. 116(4), 214–220 (1994)

    Article  Google Scholar 

  20. Ertekin, R.C., Kim, J.W., Xia, D.: Hydroelastic response of a mat-type, floating runway near a breakwater in irregular seas. In: OCEANS’99 MTS/IEEE, Seattle, Washington, IEEE, vol. 2, pp. 839–847 (1999)

  21. Ertekin, R.C., Hayatdavoodi, M., Kim, J.W.: On some solitary and cnoidal wave diffraction solutions of the Green–Naghdi equations. Appl. Ocean Res. 47, 125–137 (2014). https://doi.org/10.1016/j.apor.2014.04.005

    Article  Google Scholar 

  22. Faltinsen, O.M., Newman, J.N., Vinje, T.: Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 289, 179–198 (1995)

    Article  MATH  Google Scholar 

  23. Ferrant, P.: Runup on a cylinder due to waves and current: potential flow solution with fully nonlinear boundary conditions. In: Proceedings of 8th International Offshore and Polar Engineering Conference, ISOPE ’98, Montreal, Canada, vol III, pp. 332–339 (1998)

  24. Ferrant, P., Malenica, S., Molin, B.: Nonlinear wave loads and runup on a vertical cylinder. In Nonlinear Water Wave Interaction, Advances in Fluid Mechanics, Computational Mechanics Publishers pp. 101–135 (1999)

  25. Green, A.E., Naghdi, P.M.: On the theory of water waves. Proc. R. Soc. Lond. A 338(1612), 43–55 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  26. Green, A.E., Naghdi, P.M.: A derivation of equations for wave propagation in water of variable depth. J. Fluid Mech. 78, 237–246 (1976)

    Article  MATH  Google Scholar 

  27. Green, A.E., Naghdi, P.M.: Directed fluid sheets. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 347(1651), 447–473 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  28. Green, A.E., Naghdi, P.M.: Water waves in a nonhomogeneous incompressible fluid. J. Appl. Mech. 44(4), 523–528 (1977)

    Article  MATH  Google Scholar 

  29. Havelock, T.H.: The pressure of water waves upon a fixed obstacle on water. Proc. R. Soc. Lond. A 175, 409–421 (1940)

    Article  MATH  Google Scholar 

  30. Hayatdavoodi, M., Ertekin, R.C.: Nonlinear wave loads on a submerged deck by the Green-Naghdi equations. J. Offshore Mech. Arctic Eng. 137(1), 011102 (2015). https://doi.org/10.1115/1.4028,997

    Article  Google Scholar 

  31. Hayatdavoodi, M., Ertekin, R.C.: Wave forces on a submerged horizontal plate. Part I: theory and modelling. J. Fluids Struct. 54(April), 566–579 (2015). https://doi.org/10.1016/j.jfluidstructs.2014.12.010

    Article  Google Scholar 

  32. Hayatdavoodi, M., Ertekin, R.C.: Wave forces on a submerged horizontal plate. Part II: solitary and cnoidal waves. J. Fluids Struct. 54(April), 580–596 (2015). https://doi.org/10.1016/j.jfluidstructs.2014.12.009

    Article  Google Scholar 

  33. Hayatdavoodi, M., Ertekin, R.C., Robertson, I.N., Riggs, H.R.: Vulnerability assessment of coastal bridges on Oahu impacted by storm surge and waves. Nat. Hazards 79(2), 1133–1157 (2015). https://doi.org/10.1007/s11,069-015-1896-2

    Article  Google Scholar 

  34. Huseby, M., Grue, J.: An experimental investigation of higher-harmonic wave forces on a vertical cylinder. J. Fluid Mech. 414, 75–103 (2000)

    Article  MATH  Google Scholar 

  35. Isaacson, M.Q.: Interference effects between large cylinders in waves. In: Proceedings of 10th Offshore Technology Conference, Houston, vol. I, (Paper No. OTC 3069), pp. 185–192 (1978)

  36. Kim, J.W., Kyoung, J.H., Ertekin, R.C., Bai, K.J.: A finite-element computation of wave structure interaction between lon-crested waves of extreme height and vertical cylinders. In: Proceedings of 8th International Conference on Numerical Ship Hydrodynamics, National Academy Press, Washington, D.C., p. 11 (2003)

  37. Kim, J.W., Kyoung, J.H., Ertekin, R.C., Bai, K.J.: Finite-element computation of wave-structure interaction of steep stokes waves and vertical cylinders. J. Waterw. Port Coast. Ocean Eng. ASCE 132(5), 337–347 (2006)

    Article  Google Scholar 

  38. Kim, J.W., Ertekin, R.C., Bai, K.J.: Linear and nonlinear wave models based on hamiltons principle and stream-function theory: CMSE and IGN. J. Offshore Mech. Arctic Eng. 132(2), 021102 (2010)

    Article  Google Scholar 

  39. Kriebel, D.L.: Nonlinear wave interaction with a vertical circular cylinder. Part I: diffraction theory. Ocean Eng. 17(4), 345–377 (1990)

    Article  Google Scholar 

  40. Kriebel, D.L.: Nonlinear wave interaction with a vertical circular cylinder: wave forces. Ocean Eng. 25(7), 597–605 (1998)

    Article  Google Scholar 

  41. MacCamy, R.C., Fuchs, R.A.: Wave forces on a pile: a diffraction theory. Technical Memorandum 69, US Army Corps of Engineers (1954)

  42. Molin, B.: Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 302, 203–229 (1995). https://doi.org/10.1017/S0022112095004071

    Article  MathSciNet  MATH  Google Scholar 

  43. Maniar, H.D., Newman, J.: Wave diffraction by a long array of cylinders. J. Fluid Mech. 339, 309–330 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  44. Mei, C.C.: The Applied Dynamics of Ocean Surface Waves. World Scientific, Singapore (1989)

    MATH  Google Scholar 

  45. Mo, W., Liu, P.L.F.: Three dimensional numerical simulations for non-breaking solitary wave interacting with a group of slender vertical cylinders. Int. J. Nav. Archit. Ocean Eng. 1(1), 20–28 (2009)

    Article  MathSciNet  Google Scholar 

  46. Mo, W., Irschik, K., Oumeraci, H., Liu, P.L.F.: A 3D numerical model for computing non-breaking wave forces on slender piles. J. Eng. Math. 58(1–4), 19–30 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  47. Nadiga, B., Margolin, L., Smolarkiewicz, P.: Different approximations of shallow fluid flow over an obstacle. Phys. Fluids 8(8), 2066–2077 (1996)

    Article  MATH  Google Scholar 

  48. Naghdi, P.M.: Fluid sheets and fluid jets. In: Proceedings of 12th Symposium on Naval Hydrodynamics, National Academy of Sciences, Washington, D.C., pp. 500–515 (1978)

  49. Neill, D.R.: The nonlinear interaction of waves with multiple, vertical, in-line cylinders. Ph.D. Dissertation, Department of Ocean Engineering, University of Hawaii (1996)

  50. Neill, D.R., Hayatdavoodi, M., Ertekin, R.C.: On solitary wave diffraction by multiple, in-line vertical cylinders. Nonlinear Dyn. 91(2), 975–994 (2017). https://doi.org/10.1007/s11,071-017-3923-1

    Article  Google Scholar 

  51. Newman, J.N.: Nonlinear scattering of long waves by a vertical cylinder. In: Ed Grue, J., Gjevik, B., Weber, J.E. (eds.) Waves and Nonlinear Processes in Hydrodynamics, pp. 91–102. Springer, Dordrecht (1996)

    Chapter  Google Scholar 

  52. Newman, J.N.: The second-order wave force on a vertical cylinder. J. Fluid Mech. 320, 417–443 (1996). https://doi.org/10.1017/S0022112096007598

    Article  MATH  Google Scholar 

  53. Nwogu, O.: Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coast. Ocean Eng. 119(6), 618–638 (1993)

    Article  Google Scholar 

  54. Omer, G.C., Hall, H.H.: The scattering of a tsunami by a cylindrical island. Bull. Seismol. Soc. Am. 39(4), 257–260 (1949)

    Google Scholar 

  55. Paulsen, B.T., Bredmose, H., Bingham, H., Jacobsen, N.: Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 755, 1–34 (2014). https://doi.org/10.1017/jfm.2014.386

    Article  MathSciNet  Google Scholar 

  56. Qian, Z.M.: Numerical grid generation and nonlinear waves generated by a ship in a shallow-water channel. M.S. Thesis, Department of Ocean Engineering, University of Hawaii, pp. v+121 (1988)

  57. Qian, Z.M.: Calculations of three dimensional nonlinear ship waves and ship resistance in a shallow water channel. Ph.D. Dissertation, Department of Ocean Engineering, University of Hawaii (1994)

  58. Roddier, D.: Diffraction and refraction of solitons around a false wall. M.S. Thesis, Department of Ocean Engineering, University of Hawaii (1994)

  59. Roddier, D., Ertekin, R.C.: Diffraction and remodelization of solitons around a false wall. Chaos Solitons Fractals 10(7), 1221–1240 (1999)

    Article  MATH  Google Scholar 

  60. Schmitt, P., Bourdier, S., Whittaker, T., Sarkar, D., Renzi, E., Dias, F., Doherty, K., van’t Hoff, J., et al.: Hydrodynamic loading on a bottom hinged oscillating wave surge converter. In: The Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, International Society of Offshore and Polar Engineers, pp. 550–557 (2012)

  61. Sclavounos, P.D.: Nonlinear impulse of ocean waves on floating bodies. J. Fluid Mech. 697, 316335 (2012). https://doi.org/10.1017/jfm.2012.68

    Article  MathSciNet  MATH  Google Scholar 

  62. Sclavounos, P.D.: Nonlinear loads on a vertical circular in irregular waves. In: 31st International Workshop on Water Waves and Floating Bodies (IWWWFB), pp. 153–156 (2016)

  63. Shapiro, R.: Linear filtering. Math. Comput. 29, 1094–1097 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  64. Shields, J.J., Webster, W.C.: On direct methods in water-wave theory. J. Fluid Mech. 197, 171–199 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  65. Sun, X.: Some theoretical and numerical studies on two-dimensional cnoidal-wave-diffraction problems. M.S. thesis, Department of Ocean Engineering, University of Hawaii (1991)

  66. Swan, C., Sheikh, R.: The interaction between steep waves and a surface-piercing column. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 373(2033), 20140114 (2015)

    Article  Google Scholar 

  67. Teng, M., Wu, T.Y.: Nonlinear water waves in channels of arbitrary shape. J. Fluid Mech. 242, 211–233 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  68. Thompson, J.F., Thames, F.C., Mastin, C.W.: Boundary-fitted curvilinear system for solutions of partial differential equations on fields containing any number of arbitrary two dimensional bodies. Report No. CR2729, NASA (1977)

  69. Thompson, J.F., Warsi, Z., Mastin, C.W.: Numerical Grid Generation: Foundations and Applications. Elsevier Science Ltd, Amsterdam (1985)

    MATH  Google Scholar 

  70. Wang, K.H., Jiang, L.: Interactions of solitary waves with cylinder arrays. In: Proceedings 13th International Conference on Offshore Mechanics and Arctic Engineering, ASME, Houston, Texas, USA,, vol. I, pp. 99–107 (1994)

  71. Wang, K.H., Wu, T.Y., Yates, G.T.: Three-dimensional scattering of solitary waves by vertical cylinder. J. Waterw. Port Coast. Ocean Eng. 118(5), 551–566 (1992)

    Article  Google Scholar 

  72. Webster, W.C., Kim, D.Y.: The dispersion of large-amplitude gravity waves in deep water. In: Eighteenth Symposium on Naval Hydrodynamics, Ann Arbor, Michigan, pp. 397–416 (1991)

  73. Webster, W.C., Wehausen, J.V.: Bragg scattering of water waves by Green–Naghdi theory. In: Casey, J., Crochet, M. (eds.) Theoretical, Experimental, and Numerical Contributions to the Mechanics of Fluids and Solids, pp. 566–583. Birkhuser, Basel (1995). https://doi.org/10.1007/978-3-0348-9229-2_30

    Chapter  Google Scholar 

  74. Whitham, G.B.: Linear and Nonlinear Waves. Interscience Series on Pure and Applied Mathematics. Wiley, New York (1974)

    Google Scholar 

  75. Wiegel, R.L.: Oceanographical Engineering. Prentice-Hall International, Englewood Cliffs (1964)

    Google Scholar 

  76. Wu, D., Wu, T.Y.: Three-dimensional nonlinear long waves due to moving surface pressure. In: Proceedings of 14th Symposium on Naval Hydrodynamics, Washington, D.C., National Academy Press, Washington, D.C., 1983, pp. 103–125 (1982)

  77. Wu, T.Y.: Long waves in ocean and coastal waters. J. Eng. Mech. Div. 107(3), 501–522 (1981)

    Google Scholar 

  78. Xia, D., Kim, J.W., Ertekin, R.C.: On the hydroelastic behavior of two-dimensional articulated plates. Mar. Structures 13(4), 261–278 (2000)

    Article  Google Scholar 

  79. Xia, D., Ertekin, R.C., Kim, J.W.: Fluid-structure interaction between a two-dimensional mat-type vlfs and solitary waves by the Green–Naghdi theory. J. Fluid Struct. 24(4), 527–540 (2008)

    Article  Google Scholar 

  80. Yang, C., Ertekin, R.C.: Numerical simulation of nonlinear wave diffraction by a vertical cylinder. J. Offshore Mech. Arctic Eng. 114(1), 36–44 (1992)

    Article  Google Scholar 

  81. Yates, G.T., Wang, K.H.: Solitary wave scattering by a vertical cylinder: experimental study. In: Proceedings of 4th International Offshore and Polar Engineering Conference, ISOPE ’94, Osaka, Japan, vol. III, pp. 118–124 (1994)

  82. Zhang, J., Teng, B.: Numerical study on cnoidal wave run-up around a vertical circular cylinder. Appl. Ocean Res. 63, 276–287 (2017)

    Article  Google Scholar 

  83. Zhao, B.B., Duan, W.Y., Ertekin, R.C.: Application of higher-level GN theory to some wave transformation problems. Coast. Eng. 83, 177–189 (2014). https://doi.org/10.1016/j.coastaleng.2013.10.010

    Article  Google Scholar 

  84. Zhao, B.B., Ertekin, R.C., Duan, W.Y., Hayatdavoodi, M.: On the steady solitary-wave solution of the Green–Naghdi equations of different levels. Wave Motion 51(8), 1382–1395 (2014). https://doi.org/10.1016/j.wavemoti.2014.08.009

    Article  MathSciNet  Google Scholar 

  85. Zhao, B.B., Duan, W.Y., Ertekin, R.C., Hayatdavoodi, M.: High-level Green-Naghdi wave models for nonlinear wave transformation in three dimensions. J. Ocean Eng. Mar. Energ. 1(2), 121–132 (2015). https://doi.org/10.1007/s40,722-014-0009-8

    Article  Google Scholar 

  86. Zhong, Z., Wang, K.H.: Solitary wave interaction with a concentric porous cylinder system. Ocean Eng. 33(7), 927–949 (2006). https://doi.org/10.1016/j.oceaneng.2005.05.013

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Civil Engineering Department, School of Science and Engineering, University of Dundee, Dundee, DD1 4HN, UK

    Masoud Hayatdavoodi

  2. National Optical Astronomy Observatory, 950 N Cherry Ave., Tucson, AZ, 85719, USA

    Douglas R. Neill

  3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin, China

    R. Cengiz Ertekin

Authors
  1. Masoud Hayatdavoodi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Douglas R. Neill
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. R. Cengiz Ertekin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Masoud Hayatdavoodi.

Additional information

Communicated by William Dewar.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hayatdavoodi, M., Neill, D.R. & Ertekin, R.C. Diffraction of cnoidal waves by vertical cylinders in shallow water. Theor. Comput. Fluid Dyn. 32, 561–591 (2018). https://doi.org/10.1007/s00162-018-0466-0

Download citation

  • Received: 03 January 2018

  • Accepted: 29 May 2018

  • Published: 13 June 2018

  • Issue Date: October 2018

  • DOI: https://doi.org/10.1007/s00162-018-0466-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Keywords

  • Cnoidal wave
  • Multiple in-line vertical circular cylinders
  • Wave force and moment
  • Boussinesq equations
  • Green–Naghdi equations
Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Advertisement

Search

Navigation

  • Find a journal
  • Publish with us
  • Track your research

Discover content

  • Journals A-Z
  • Books A-Z

Publish with us

  • Journal finder
  • Publish your research
  • Open access publishing

Products and services

  • Our products
  • Librarians
  • Societies
  • Partners and advertisers

Our brands

  • Springer
  • Nature Portfolio
  • BMC
  • Palgrave Macmillan
  • Apress
  • Discover
  • Your US state privacy rights
  • Accessibility statement
  • Terms and conditions
  • Privacy policy
  • Help and support
  • Legal notice
  • Cancel contracts here

Not affiliated

Springer Nature

© 2025 Springer Nature