A surrogate model to accelerate non-intrusive global–local simulations of cracked steel structures

Abstract

Physics-based digital twins often require many computations to diagnose current and predict future damage states in structures. This research proposes a novel iterative global–local method, where the local numerical model is replaced with a surrogate to simulate cracking quickly on large steel structures. The iterative global–local method bridges the scales from the operational level of a large steel structure to that of a cracked component. The linear global domain is efficiently simulated using static condensation, and the cracked local domain is quickly simulated using the adaptive surrogate modeling method proposed herein. This work compares solution time and accuracy of the proposed surrogate iterative global–local method with a reference model, a submodeling model, and an iterative global–local method with no surrogate model for the local domain. It is found that the surrogate iterative global–local method gives the fastest solution time with comparatively accurate results.

1 Introduction

With current computational mechanics technology, physics-based digital twins can diagnose and predict crack damage in structures. However, techniques to infer such information require the exploration of many crack state possibilities, which is computationally expensive. This research proposes a surrogate iterative global–local method to quickly simulate many instances of a stationary crack on a large steel structure.

This research uses a miter gate problem as its case study, as shown in Fig. 1, although the developed approach is easily applicable to other structures. Miter gates are critical components of river navigation that swing open and shut to allow boat passage through a navigation lock chamber. When closed, miter gates act as damming surfaces, allowing the water in the lock chamber to rise or fall. These two processes combined allow the lock chamber to act as a boat elevator, allowing boats to bypass dams and their accompanying water-level differences. Some of the most important structural parts of the gates are submerged during operation, making visual inspection difficult, leaving an information gap that digital twin technology aims to fill. This paper describes the miter gate example problem more fully in Sect. 3.

Fig. 1

An open miter gate

The main problem in simulating large steel structural performance (e.g., miter gate in Fig. 1) with component-scale cracks is the separation in length scales. Miter gate structures may be tens of meters tall and wide, but their (possibly stable) cracks may be as long as a few cm. Thus, the structure and crack features are two orders of magnitude different in scale, complicating numerical model discretization and increasing computational cost. In the miter gate numerical model, a small solid cracked part (local region) is tied to a pristine shell structure (global region) in Abaqus. A fully-coupled at-scale simulation must include the global region’s behavior to find crack effects, greatly adding to the computational burden of the digital twin.

Zooming or submodeling can be used to separate the cracked portion of the structure from the pristine portion for reduced computational cost. The submodeling method transfers the global region solution to the shared boundary with the local region. This is computationally cheap and built into several commercial softwares including Ansys and Abaqus, but it fundamentally relies on Saint-Venant’s principle, which states the difference between the effects of two different but statically equivalent loads becomes very small at sufficiently large distances from load. It will be shown that this principle does not hold for the miter gate example.

A generalization of the submodeling method is the iterative global–local (IGL) method (Allix and Gosselet 2020). The IGL method provides a mechanism to obtain much more accurate solutions than submodeling via a similar numerical strategy: the global gate’s displacements are imposed on the local model boundary. Then a feedback loop finds the local boundary reaction, compares it to the global boundary traction, and applies the calculated immersed surface force to a new global computational job. Iterations can be performed until the solution is sufficiently accurate. The basic process is shown in Fig. 2. The IGL method converges to the reference combined problem given enough iterations. Thus, the IGL method can be viewed as a bridge between the submodeling and tying methods, providing increased accuracy over submodeling at the expense of increased computational cost over submodeling.

Fig. 2

Iterative global–local overview

Previous IGL method work has looked at non-intrusively enhancing solid domains with XFEM cracks using XFEM/GFEM (Duarte et al. 2001; Moes et al. 1999; Fillmore and Duarte 2018; Gupta et al. 2012). However, those methods each encountered limitations not affecting the IGL method. XFEM/GFEM crack modeling requires less particular local mesh refinement than quarter node elements (Duarte et al. 2001; Moes et al. 1999; Henshell and Shaw 1975; Barsoum 1976), and therefore it is used in this work. Additionally, the IGL method has been used successfully to simulate non-linearities in the local domain with a linear global domain (Gendre et al. 2009).

The IGL method can be described as non-intrusive because of the ease with which research software may be combined with commercial software. This allows synergy between the robustness and broad applicability of the commercial software and the specificity of the research software. Also, the non-linear case clearly lends itself to speed increases since Newton–Raphson iterations may be performed locally, reducing the problem size dramatically. Within the context of large structures typically modeled as shells, the IGL method has been successfully used to connect shell global domains to solid local domains with welds (Li et al. 2021a). The IGL method has also been used to tie a shell aircraft geometry to a shell local domain with a sub-local solid domain tied into the local domain (Guinard et al. 2018). This paper describes the IGL methodology in Sect. 2. Finally, an alternative method to IGL for crack representation (i.e., a multigrid XFEM method) is proposed in Passieux et al. (2013).

Fig. 3

Surrogate iterative global–local overview

The local cracked region in the miter gate will be modeled linearly using XFEM/GFEM, so the speed advantages of quarantining non-linear regions to the local domain cannot be exploited. Therefore, the IGL method cannot be assumed to be faster than the reference tying method. To accelerate the local-domain solution, this research proposes the novel modeling the IGL local domain using a surrogate model rather than a physics-based model. The surrogate model is trained on the local physics-based (crack) numerical results (not necessarily from a linear analysis). This surrogate model may then be used within the IGL framework to dramatically reduce local-domain solution time. In fact, the non-intrusive nature of the IGL method (Allix and Gosselet 2020; Gendre et al. 2009, 2011; Gosselet et al. 2018; Li et al. 2021a) facilitates easy implementation of the surrogate model.

Surrogate models, such as a Kriging method (Hu and Mahadevan 2016; Li et al. 2021b), neural networks (Li et al. 2017), and deep learning approaches (Chen et al. 2020), have been extensively studied in structural analysis and design optimization to reduce the required computational effort, especially in the presence of uncertainty (Hu and Mahadevan 2017; Zhang and Taflanidis 2019). Various approaches have been proposed in the past decade to build an efficient yet accurate surrogate model (Sadoughi et al. 2018; Li et al. 2021a; Viana et al. 2021). Some multiscale frameworks simulate material-scale damage by using a surrogate model handle material properties and damage information (Yan et al. 2020; El Said and Hallett 2018). To the best of our knowledge, however, surrogate modeling in an IGL framework has not been reported. This paper describes a surrogate-based IGL methodology in Sect. 4 to fill this void.

Accelerating global domain linear solutions is somewhat easier using static condensation. Interactions between sub-regions to solve the aggregate problem can be accelerated using static condensation (Bjorstad and Widlund 1986; Gendre et al. 2009; Wyart et al. 2008). Within the IGL framework, this research utilizes static condensation to accelerate solution of the linear global problem, as discussed in Sect. 2.4. The use of a surrogate model for the local domain and static condensation for the global domain results will be referred to as the surrogate iterative global–local (SIGL) method for the rest of this paper. SIGL has trivial computational time for each IGL method iteration, making the IGL method extremely fast, relatively speaking. The basic SIGL process is shown in Fig. 3.

Four possible techniques have been mentioned to solve a problem in the class posed within this work: (1) reference tying method, (2) submodeling method, (3) IGL method, and (4) a proposed surrogate IGL method. The accuracy and speed of each of these approaches are shown and discussed in Sect. 5.

The remainder of this paper is organized as follows: Section 2 presents the reference tying, submodeling method, and the IGL algorithm. Using the miter gate problem given in Sect. 3 as an example, Sect. 4 presents the proposed surrogate model-based IGL framework. Results comparing the different modeling methods is presented and discussed in Sect. 5. Section 6 gives the conclusions.

2 Modeling methodologies

2.1 Reference problem (shell-solid tying)

The reference problem to be solved is a shell geometry tied to a small solid geometry with a feature of interest and boundary conditions, as shown in Fig. 4. Large steel structures will have much larger shell domain $\Omega _\text{SH}$ compared to the solid domain $\Omega _\text{S}$. Also, body loads may be included although they are not shown in the figure. Commercial software such as Abaqus provide the tools to solve this problem for many different features of interest, including cracks. The tying method couples a solid surface to a shell edge where the shell normal is perpendicular to the solid surface normal. The constraints couple the displacement and rotation of each shell node to the average displacement and rotation of the solid surface near the shell node (Abaqus 2021).

Fig. 4

Reference problem with shell domain $\Omega _\text{SH}$, solid domain $\Omega _\text{S}$, shell-to-solid tied boundary $\Gamma _\text{SH}$, feature of interest, Neumann boundary condition $\Gamma _\text{N}$, and Dirichlet boundary condition $\Gamma _\text{D}$

2.2 Submodeling methodology

The submodeling method has a coarsely discretized global domain $\Omega _\text{G}$ and a finely discretized local domain $\Omega _\text{LSH}\cup \Omega _\text{LS}=\Omega _\text{L}$ containing the feature of interest within $\Omega _\text{LS}$ as shown in Fig. 5. The displacements and rotations are solved for in the global domain and then the displacements and rotations along $\Gamma _\text{GL-G}$ are applied to the local domain along $\Gamma _\text{GL-L}$. The solution of the local domain reflects the effects of the feature of interest. Due to the lack of any feedback mechanism to the global domain, this solution tends to underestimate the effects of the feature of interest and may not be sufficiently accurate. However, the numerical solution time is likely faster than the reference problem. If it is assumed that the number of flops is on the order of the number of degrees of freedom cubed $f_\text{ref}=O(n^3)$ due to factorization, then dividing n into $n\approx n_\text{G} + n_\text{L}$ gives the submodeling number of flops as $f_\text{sub}=O(n_\text{G}^3)+O(n_\text{L}^3)$. Therefore $f_\text{ref}>f_\text{sub}$.

Fig. 5

Submodeling problem with global domain $\Omega _\text{G}$, local shell domain $\Omega _\text{SH}$, local solid domain $\Omega _\text{S}$, shell-to-solid tied boundary $\Gamma _\text{SH}$, feature of interest, Neumann boundary condition $\Gamma _\text{N}$, Dirichlet boundary condition $\Gamma _\text{D}$, global–local boundary $\Gamma _\text{GL}$, and local Dirichlet boundary condition $\Gamma _\text{GL-L}$

As shown in Fig. 5, the local domain $\Omega _\text{L}$ is subdivided into a solid local domain $\Omega _\text{LS}$ with the feature of interest and a shell local domain $\Omega _\text{LSH}$ to act as a buffer zone between the global discretization and local discretization. The two subdomains are tied along their shared boundary $\Gamma _\text{SH}$ using built-in Abaqus shell-to-solid tie constraints.

2.3 Iterative global–local methodology

The IGL method is a generalization of the zooming/submodeling method which incorporates a feedback loop into the global domain. This feedback loop improves accuracy but increases computational cost. The IGL method utilizes a local domain with local features of interest and fine discretization along with a global domain with a coarse discretization. The corresponding problem to Fig. 5 is shown in Fig. 6. The boundary between the global and local domains $\Gamma _\text{GL}$ facilitates exchange of displacement and reaction forces between the global and local problems. Note that the local domain utilizes the technique in Guinard et al. (2018) to facilitate shells in the global region and solids in the local region near the feature of interest.

Fig. 6

Iterative global–local algorithm illustrated using $\Omega _\text{G}$, $\Omega _\text{LSH}$, $\Omega _\text{LS}$, feature of interest, $\Gamma _\text{N}$, Dirichlet boundary condition $\Gamma _\text{D}$, $\Gamma _\text{GL-G}$, $\Gamma _\text{GL-L}$, and $\Gamma _\text{SH}$. The top large arrow denotes the application of displacements and rotations from the global solution to the local problem. The bottom large arrow denotes the application of the residual between: (a) the local solution reaction forces and moments and (b) the global traction forces and moments to the global problem. This process is repeated until convergence is reached

The IGL algorithm is given in Algorithm 1 where ${{\textbf {p}}}_\text{j}$ is immersed surface force at $\Gamma _\text{GL-G}$, $\omega _\text{j}$ is relaxation parameter that accelerates convergence, ${{\textbf {u}}}_\text{j}^G$ is global displacement at $\Gamma _\text{GL-G}$, $\varvec{\lambda }_\text{j}^L$ is local reaction at $\Gamma _\text{GL-L}$, and $\varvec{\lambda }_\text{j}^{GA}$ is the auxiliary reaction at $\Gamma _\text{GL-A}$ shown in Fig. 7. Algorithm 1 expounds upon the values exchanged between $\Omega _\text{G}$ and $\Omega _\text{L}$. It is generally accepted that Aitken’s Delta-Squared method provides robust convergence for this algorithm (Allix and Gosselet 2020; Duval et al. 2016; Gosselet et al. 2018; Liu et al. 2014).

This algorithm shows that part of the first iteration of IGL constitutes the zooming/submodeling method. To compare accuracy between the two and the reference solution, values specific to the feature of interest will be used, specifically for cracks stress intensity factors (SIF).

For a linear problem IGL may be faster than the reference problem under ideal conditions, e.g., the commercial software can save the factorized matrix. The speed increase depends on the number of iterations i and $n_\text{G}$, $n_\text{L}$, and n. Considering factorization and forward and backward substitution since it may be significant for iterations within IGL, $f_\text{IGL}=O(n_\text{L}^3+n_\text{G}^3 +i \times \left( n_\text{L}^2+n_\text{G}^2\right)$. Directly comparing this with the tying method $f_\text{ref}=O((n_\text{L}+n_\text{G} )^3+(n_\text{L}+n_\text{G} )^2 )$ one can see the rather precarious situations under which IGL may be faster than the tying method. Now, assume that these estimates on the order of solution perfectly represent solution time. We take that IGL solution time must be less than the tying, $n_\text{L}^3+n_\text{G}^3+i\times (n_\text{L}^2+n_\text{G}^2 )<n_\text{L}^3+3n_\text{L}^2 n_\text{G}+3n_\text{L} n_\text{G}^2+n_\text{G}^3+n_\text{L}^2+2n_\text{L} n_\text{G}+n_\text{G}^2$. Solving this for i gives

$$\begin{aligned} i<\frac{3n_\text{L}^2 n_\text{G}+3n_\text{L} n_\text{G}^2}{n_\text{L}^2+n_\text{G}^2 }+1. \end{aligned}$$

(1)

If either $n_\text{L}$ or $n_\text{G}$ is much greater than the other, $i<4$ for faster IGL solution of the system of equations. If $n_\text{L}$ approaches 0 (local problem disappears) $i<1$. This motivates the numerical context within which IGL is useful: the global domain is so large that the local domain likely requires immense detail for the feature of interest. Now, the global maximum for m is along the line $n_\text{L}=n_\text{G}$ which gives $i<6n_\text{L}+1$ iterations. Now this is not exact arithmetic on the time to solution of the system, but demonstrates the likely speed advantage of IGL for linear problems. In this research, such ideal conditions are achieved using static condensation, which has the added benefit of reducing the degrees of freedom in the solve for the global system of equations.

Fig. 7

Iterative global–local algorithm auxiliary domain $\Omega _\text{GA}$ used for the calculation of global traction

2.4 Static condensation of global domain in IGL method

The IGL algorithm provides clear computational benefits with localized non-linearity, since Newton–Raphson iterations need to be performed on only the much smaller local domain. However, this research shows that the IGL method may be much slower than the tying method in a linear local problem. In this research, the XFEM crack local problem is linear and computationally expensive, which makes IGL possibly slower than the tying method. In an attempt to accelerate the IGL method, static condensation can be applied to both the global and local stiffness matrices since both are linear. Statically condensing $\Omega _\text{G}$ requires leaving the degrees of freedom at the nodes along $\Gamma _\text{GL}$ uncondensed. Then global Neumann boundary conditions can be applied at those degrees of freedom as well as the immersed surface force at each iteration $p_\text{i}$. Then, the global displacement along $\Gamma _\text{GL}$ (${\varvec{u}}_\text{i}^G$) is obtained directly from the condensed matrix.

In the example problem presented in this research, there may be damage in one boundary condition region. When damage is not present, a pin boundary condition is applied; when damage is present, the pin boundary condition is removed. This is compatible with static condensation by leaving all nodes along the boundary condition uncondensed and applying the pins on the static condensation system of equations.

While static condensation demands a large upfront cost, the speed improvement comes with the many IGL iterations performed over the many permutations of a Monte Carlo analysis or training process. However, applying static condensation to the local-domain stiffness matrix has some caveats. First, the used commercial software does not support static condensation with XFEM, although it is theoretically possible. Second, a unique static condensation must be computed for each crack length, which may be faster than the reference solution.

Since the static condensation of a global stiffness matrix can consider different load cases and levels of damage along the boundary condition, only one global static condensation step is necessary per local domain. Then the same reduced stiffness matrix can be used over the permutations of load cases, damaged boundary condition, and IGL iterations. Thereby, the static condensation of the FEM discretization of the global domain saves computational cost. However, it is shown in Sect. 5 that the IGL solution of a problem with only one permutation of the load cases and damaged boundary conditions saves computational effort.

3 Problem definition: application to a miter gate

3.1 Miter gate operation, load state, and feature of interest

Miter gates are navigational hydraulic steel structures critical to river traffic. They function as boat “elevators” that allow boats to bypass dams and navigate up or down river. Figure 8 shows how miter gates open and close. The gudgeon and pintle (seen in Fig. 9) form a hinge about which the gate rotates. More detailed information about pintle behavior can be found in Fillmore and Smith (2021). When open, boats can enter or leave the lock chamber. When closed, the lock chamber can be filled or emptied (on the upstream side) while the miter gate acts as a damming surface. The resulting hydrostatic pressure pushes the two leaves together along their miter and pushes each leaf into the wall along the quoin. More detailed information about quoin behavior can be found in Eick et al. (2019).

Fig. 8

Miter gate top view with swinging motion

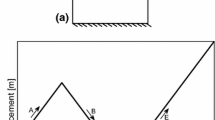
Miter gates’ largest cyclic loads are from the filling and emptying of lock chambers as boats are lifted or lowered. The resulting cyclic stresses contribute to fatigue cracking. Miter gates are welded structures, so the heat-affected zones greatly accentuate the cyclic stresses. However, in this example, a region of the leaf is selected that naturally experiences tension to reduce complexity resulting from weld residual stresses. This portion of the leaf is near the bottom center. If each leaf is viewed as a beam (Fig. 8) with distributed load, the greatest tension in the leaf will occur on the downstream side at the middle of the leaf.

Fig. 9

Miter gate downstream side view. Photograph courtesy of John Cheek, USACE

A finite element model representing the Greenup downstream miter gate is shown in Fig. 10. The boundary conditions of the miter gate are set up to simulate the in-situ environment of a hanging gate. The miter gate rotates around the axis created by the anchorage pin and pintle as shown in Fig. 8. The pintle, a ball and socket joint, takes all of the vertical gravity load. The pintle is represented by applying a multi-point constraint (MPC) from the center of the ball to the portions of the horizontal girder with which the socket connects. Then, the center of the ball is restrained from translating in the x-, y-, and z-directions. The anchorage links are embedded in concrete at the top of the gate. This is represented by restraining translation in the x-, y-, and z-directions.

Fig. 10

Miter gate boundary conditions

The strut pin is attached to a strut arm that opens and closes the gate. The strut pin can rotate around the z-axis. When the gate is closed, the strut arm applies resistance at − 43° from the negative x-direction on the gate. The strut pin is modeled by applying an MPC from the top of the strut pin to the enveloping top lug and a separate MPC from the bottom of the strut pin to the enveloping bottom lug., Then the center of the strut pin is restrained from translating − 43° from the negative x-direction.

Hydrostatic pressure is applied on the upstream plate of the gate, called the skin plate as shown in Fig. 11. The upstream hydrostatic pressure is denoted $h_\text{up}$ and the downstream hydrostatic pressure is denoted $h_\text{down}$. When the gate holds enough water in the lock chamber, the miter contact block of both gate leaves comes into contact and a symmetric pin is assumed preventing translational movement − 18° from the x-direction. The two gate leaves act as an arch, experiencing more axial compression under more hydraulic head. This compression causes the gate to thrust in the lock wall contact block. The wall resists horizontal movement in the x- and y-directions, which is represented in the model with pins that resist translation in the x- and y-directions.

Fig. 11

Miter gate hydrostatic pressure from upstream and downstream water levels

The contact of the quoin contact block with the wall is idealized using pin boundary conditions as shown in Fig. 12. Often, the bottom portion of the quoin becomes damaged so that it cannot properly contact the wall. This lack of contact is idealized by not applying the pin boundary conditions. The length of this damaged region is denoted $l_\text{dmg}$.

Fig. 12

Damage in the quoin contact block

Figure 13 shows the reference discretization with a zoom-in of the crack region. The shell elements used over much of the gate are reduced-integration quadrilaterals with element size six inches. Where the crack is defined linear, hexahedral elements are used with element size 0.0625 in. The mesh discretization has 201, 463 elements and 211, 372 nodes. The IGL discretization is effectively identical to the reference, with an identical mesh discretization in $\Omega _\text{G}$ and $\Omega _\text{L}$.

Figure 13 also shows the location of the crack used for this example. The crack occurs along the bottom web edge of the second from bottom girder as shown in Fig. 13. The crack has a straight front, extending through the entire 3/4 in thickness of the plate. The crack length is variable, but the largest possible length through the web bottom is 4 in.

Miter gates are fabricated by welding mild steel plates together. The local weld geometries are ignored in this research. A linear material model is used with the Young’s modulus as $E=29,000$ ksi and the Poisson ratio as 0.3.

Fig. 13

Mesh discretization of reference miter gate model

Figures 14, 15, 16, and 17 help clarify how IGL is used in this example. Figure 14 shows the global domain along with the immersed surface force $p_\text{i}$ resulting from the IGL algorithm. The global domain does not contain the crack and is only coarsely discretized in the crack’s coordinates $\Omega _\text{GA}$. Outside of $\Omega _\text{GA}$, the global domain’s geometry and discretization match up exactly with the reference model.

Fig. 14

IGL global miter gate model with zoom-in of area of interest. No crack is included in the area of interest, but the shown purple arrows along boundary $\Gamma _\text{GL}$ are the $p_\text{i}$ forces that relay the effects to the global model

The feature of interest is the crack, which is only explicitly represented in the local model in Fig. 15. The geometry and discretization of the shell domain $\Omega _\text{LSH}$ and the solid domain $\Omega _S$ line up exactly with the reference model in the corresponding region. Also, the nodes of the FEM global mesh along $\Gamma _\text{GL}$ line up with the nodes of the FEM local mesh along $\Gamma _\text{GL-L}$ exactly. Because shell elements are used, such matching meshes along the 1-dimensional interface are easy to produce in Abaqus. Displacements and rotations from the global model at the IGL step are applied along $\Gamma _\text{GL-L}$.

Fig. 15

Local miter gate model with contour integral crack representation. The crack is located in the solid subdomain $\Omega _S$. The global displacement solution $u_\text{i}^G$ is applied along the global–local boundary $\Gamma _\text{GL}$

Figure 16 shows the global auxiliary domain. This domain matches the $\Omega _\text{GA}$ in Fig. 16 exactly, i.e., there is no crack and has the same mesh discretization. When the displacements and rotations from the global solution are applied along $\Gamma _\text{GL}$, this domain helps to calculate the reaction forces of $\Omega _\text{GA}$ easily, particularly when sophisticated post-processing capabilities are not available.

Fig. 16

Global auxiliary miter gate model. The global displacement solution $u_\text{i}^G$ is applied along the global–local boundary $\Gamma _\text{GL}$

The IGL fixed point iteration algorithm with Aitken’s Delta-Squared method is shown in the context of the cracked miter gate in Fig. 17. The boundary conditions for the global domain include damaged gap length $l_\text{dmg}$, and upstream $h_\text{up}$ and downstream $h_\text{down}$ water heights that result in ${\varvec{f}}^G$. The local domain has a certain crack length a. For the first iteration of IGL or the submodeling method, $p_\text{i}=0$. The resulting displacements and rotations along $\Gamma _\text{GL}$ are applied to the local and auxiliary global models. These models give the local reactions and global reactions, respectively. The residual between them is found. The local model and global auxiliary model also have the displacements from the global model solution $u_\text{i}^G$ applied along $\Gamma _\text{GL}$.

Fig. 17

Illustrated IGL fixed point iteration algorithm with Aitken’s Delta-Squared method for miter gate with global, local, and global auxiliary mesh discretizations. The global domain has $l_\text{dmg}$, $h_\text{up}$, and $h_\text{down}$ parameters. The local domain has parameter a

3.2 Calculating the stress intensity factor

The stress intensity factor is calculated using built-in Abaqus technology. There are 13 nodes through the thickness of the cracked plate, and through the rest of this paper the middle node will be considered. Four contours are generated per node, and the first SIF mode, $K_1$, is recorded. The Abaqus default contour integral method, the line integral method is used. In order to measure error of the methods considered in this research, the SIF relative error with the reference solution is calculated as $e_\text{K}=\frac{\Vert K_{1-\text{ref}}-K_{1-\text{IGL}}\Vert }{K_{1-\text{ref}}}$, where $K_{1-\text{ref}}$ is the SIF value extracted from the reference model and $K_{1-\text{IGL}}$ is from IGL.

4 Surrogate iterative global–local methodology

The aforementioned IGL algorithm is computationally expensive for probabilistic analysis (e.g., reliability analysis, uncertainty quantification, model updating), since the model needs to be executed thousands of times. A straightforward way to overcome the computational challenge of the IGL method is to directly build a surrogate model for the IGL model as a whole by treating the model as a black box. The direct surrogate modeling method, however, has the following three major drawbacks:

• 1. Whenever there is a change in the global model, the original surrogate model will become inapplicable and needs to be retrained;

• 2. As a purely data-driven approach, the direct surrogate modeling method does not preserve the physical information in the global model;

• 3. The training time is much longer. Generating training samples for the direct surrogate modeling method requires full runs of the IGL, which itself requires a number of iterations to converge.

This section proposes a hybrid surrogate modeling method to tackle the computational challenge in the IGL method and overcome the limitations of the direct surrogate modeling method. In the proposed method, the FE process of global domain is kept to capture the physical response of the global domain under several boundary conditions, while the non-linear behavior of the local domain is modeled using Gaussian Process Regression (GPR) (Santner 2003; Williams and Rasmussen 2006). As for this paper, the GP package from scikit-learn is used to build the surrogate models (Pedregosa 2011). Because that the local FEM process was used repeated in IGL iterations, the performance of the surrogate model must be carefully calibrated without introducing additional system error. The proposed method consists of two main steps, namely (1) surrogate modeling and refinement in the local domain; and (2) integration of physics-based global model and data-driven local model for IGL implementation. In what follows, more details are provided about the proposed surrogate-based iterative global–local methodology.

4.1 Surrogate modeling in the local domain

As shown in Fig. 17, the input of the local-domain FE model consists of the displacements ${\varvec{u}}^G$ from the global model solution and given crack length a imposed to the local domain. The output, correspondingly, is composed of the reaction forces $\varvec{\lambda }^L$ from the local model solution. The goal of surrogate modeling in the local domain is to efficiently map ${\varvec{u}}^G$ and a to $\varvec{\lambda }^L$ using surrogates without solving the computationally expensive local FE model repeatedly.

4.1.1 Training data collection

The local boundary condition solved from the global model is dominated by the hydrostatic pressure and the quoin block damage. Meanwhile, the crack length determines the corresponding response from the local model. Overall, the physics of the whole structural system in this case is affected by four parameters, i.e., $h_\text{up}$, $h_\text{down}$, $l_\text{dmg}$, and a. Different combinations of such parameters induce different physical behaviors of local model, leading to input–output (IO) relations for the surrogate models. Directly building and training surrogate models can be time-intensive as such high-dimensional space is hard to be sufficiently sampled. To overcome this challenge, we first generate N samples in the 4-D space constructed by $h_\text{up}$, $h_\text{down}$, $l_\text{dmg}$, and a using the Latin hyper-cube sampling method. In this study, 400 samples are first generated as shown in Fig. 18, assume that the IGL algorithm needs $n_i$ iterations to converge for the i-th sample, $\forall i = 1,\;2,\; \cdots ,\;N$. The intermediate training data can be denoted as ${\varvec{u}}_\text{i}^G\in {\mathbb {R}}^{(n_\text{i}\times M_\text{DOF})}$ and $\varvec{\lambda }_i^L\in {\mathbb {R}}^{(n_\text{i}\times M_\text{DOF})}$, where $M_\text{DOF}$ is the total DOFs of the local boundary $\Gamma _\text{GL}$. In this example, 200 samples are generated with the parameter ranges as $h_\text{up} \sim [432,720]$ in, $h_\text{down} \sim [120,360]$ in, $l_\text{dmg} \sim [0,150]$ in, and $a \sim [0.5,4]$ in, where [lb, ub] represents variation lower bound lb and upper bound ub.

Fig. 18

Collecting ${\varvec{u}}^G, {\varvec{\lambda }}^{L}$, and SIF training data from the physics model

Let the total number of data collected for ${\varvec{u}}^G$ and ${\varvec{\lambda }}^L$ be $N_T$ (i.e., $N_T=\sum _{i = 1}^N {{n_i}}$), we then have training data from the N simulations as

$$\begin{aligned} \begin{aligned} {\mathbf {X}}&= (\underline{{\varvec{u}}}^G,{\mathbf {a}})\\&=[({\varvec{u}}_1^G,a_1),({\varvec{u}}_2^G,a_2),...,({\varvec{u}}_{N_T}^G,a_{N_T})]\\&\in {\mathbb {R}}^{(N_{T}\times (M_{DOF}+1))}, \\ {\mathbf {Y}}&= \underline{\varvec{\lambda }}^L=[\varvec{\lambda }_1^L,\varvec{\lambda }_2^L,...\varvec{\lambda }_{N_T}^L]\in {\mathbb {R}}^{({N_T}\times M_{DOF})}, \\ \end{aligned} \end{aligned}$$

(2)

where $M_\text{DOF}$ is the total DOFs of the local boundary $\Gamma _\text{GL}$. Note that the data are organized in rows, i.e., the total number of rows represents the length of the data and the total number of columns represents the dimension of the data.

4.1.2 Data compression and latent space representation

In general, as the input dimension of the surrogate model increases, the training data required to fully characterize the IO relationship grow exponentially. According to the collected training data in the case of miter gate, the local boundary $\Gamma _\text{GL}$ contains $120\times 6$ DOFs ($M_\text{DOF}$ = 720) resulting in a 721-dimensional input and a 720-dimensional output. The high-dimensional input and output make the construction of accurate surrogate models in the local domain very challenging. Thus, instead of directly building surrogate models for ${\varvec{u}}^G$ and ${\varvec{\lambda }}^L$, dimension reduction method is necessary to map the IO relationship into a low-dimensional latent space. Numerous contributions have been made to compress dataset from higher dimensional matrix to lower dimensional matrix with various dimension reduction techniques, such as singular value decomposition, independent component analysis, and auto-encoder (Fodor 2002; Vega et al. 2021). Considering its computational cost as well as stability, SVD is adopted in this paper. However, compression in the developed approach is not limited to SVD, but can be accomplished with other dimension reduction techniques as well.

In SVD, the data collected in Eq. (2) is decomposed as

$$\begin{aligned} \begin{aligned}&\underline{{\varvec{u}}}^G = {{{\varvec{W}}}_u}{{{\varvec{E}}}_u}{{\varvec{V}}}_u^T, \\&\underline{\varvec{\lambda }}^L = {{{\varvec{W}}}_{\lambda }}{{{\varvec{E}}}_{\lambda }}{{\varvec{V}}}_{\lambda }^T, \\ \end{aligned} \end{aligned}$$

(3)

where ${{{\varvec{W}}}_u},{{{\varvec{W}}}_{\lambda }}\in {\mathbb {R}}^{(N_\text{T}\times N_\text{T})}$ and ${{\varvec{V}}}_u^T,{{\varvec{V}}}_{\lambda }^T\in {\mathbb {R}}^{(M_{DOF}\times M_\text{DOF})}$are orthogonal matrices, and ${{{\varvec{E}}}_u},{{{\varvec{E}}}_{\lambda }}\in {\mathbb {R}}^{(N_\text{T}\times M_\text{DOF})}$ are rectangular diagonal matrices. Note that the crack length in the input data is not compressed with the whole matrix due to its significance.

Fig. 19

Dimension reduction strategy of the proposed method compared with IO of FEM local model

After the decomposition given in Eq. (3), a low-rank matrix approximation can be further determined, namely

$$\begin{aligned} \begin{aligned}&{\tilde{\underline{{\varvec{u}}}}^{\prime G}} = {{{\varvec{W}}}_u}{\tilde{{\varvec{E}}}_u}{{\varvec{V}}}_u^T, \\&{\tilde{\underline{\varvec{\lambda }}}^{\prime L}} = {{{\varvec{W}}}_{\lambda }}{\tilde{{\varvec{E}}}_{\lambda }}{{\varvec{V}}}_{\lambda }^T, \\ \end{aligned} \end{aligned}$$

(4)

where ${\tilde{{\varvec{E}}}_u}\in {\mathbb {R}}^{(N_\text{T}\times N^\prime _\text{u})}$ and ${\tilde{{\varvec{E}}}_{\lambda }}\in {\mathbb {R}}^{(N_\text{T}\times N^\prime _{\lambda })}$ are the same matrices as ${{{\varvec{E}}}_u},{{{\varvec{E}}}_{\lambda }}$ except that they contain only $N^\prime _\text{u}$ and $N^\prime _{\lambda }$ largest singular values, respectively (the other singular values are replaced by zero). Figure 20 illustrates how the important features of the data can be represented by a low-rank matrix from the SVD.

Fig. 20

Illustration of the importance values of different features in the matrix represented by the singular values

As shown in Fig. 19, the corresponding reduced-order the displacement and reaction force, denoted ${\varvec{u}}^{\prime G}$ and $\varvec{\lambda }^{\prime L}$, can be represented by truncating the orthogonal matrices ${{\varvec{W}}_u},{{\varvec{W}}_{\lambda }}$ based on their ranks

$$\begin{aligned} \begin{aligned}&{{{\varvec{W}}}_u}\in {\mathbb {R}}^{(N_\text{T}\times N_\text{T})}\rightarrow {{{{\varvec{W}}^\prime }_u}}\in {\mathbb {R}}^{(N_\text{T}\times N^\prime _\text{u})}\rightarrow {\varvec{u}}^{\prime G}, \\&{{{\varvec{W}}}_{\lambda }}\in {\mathbb {R}}^{(N_\text{T}\times N_\text{T})}\rightarrow {{{{\varvec{W}}^\prime }_{\lambda }}}\in {\mathbb {R}}^{(N_\text{T}\times N^\prime _{\lambda })}\rightarrow \varvec{\lambda }^{\prime L}, \\ \end{aligned} \end{aligned}$$

(5)

where $N_{\text{u}^\prime }$ and $N_{\lambda ^\prime }$ are the dimensions of ${\varvec{u}}^{\prime G}$ and $\varvec{{\lambda }}^{\prime L}$ after reduction. The decoders and encoders are defined as the matrices that allow the data to transform between low-dimensional and high-dimensional spaces through matrix multiplication. Written explicitly,

$$\begin{aligned} \begin{aligned}&\text {Decoder}_\lambda ={{{\varvec{E}}^\prime }_{\lambda }}{{\varvec{V}}^\prime }_{\lambda }^T, \\&\text {Encoder}_u=({{{\varvec{E}}^\prime }_u}{{\varvec{V}}^\prime }_u^T)^{\dagger }, \\&{{\varvec{u}}^{G}}={{\varvec{u}}^{\prime G}} \times \text {Decoder}_u, \\&{\varvec{\lambda }^{L}}={\varvec{\lambda }^{\prime L}} \times \text {Decoder}_\lambda , \\&{{\varvec{u}}^{\prime G}}={{\varvec{u}}^{G}} \times \text {Encoder}_u, \\&{\varvec{\lambda }^{\prime L}}={\varvec{\lambda }^{L}} \times \text {Encoder}_\lambda , \\ \end{aligned} \end{aligned}$$

(6)

where $({{{\varvec{E}}^\prime }_u}{{\varvec{V}}^\prime }_u^T)^{\dagger }$ is the (Moore–Penrose) pseudoinverse (Moore 1920) of ${{{\varvec{E}}^\prime }_u}{{\varvec{V}}^\prime }_u^T$, which extends matrices inversion to non-square matrices (the decoders are non-square matrices in most cases).

The latent space of the surrogate model now can be presented as

$$\begin{aligned} \begin{aligned} \mathbf {X^\prime }&= \underline{{\varvec{u}}}^{\prime G} \\&= [({\varvec{u}}_1^{\prime G},a_1),({\varvec{u}}_2^{\prime G},a_2),...,({\varvec{u}}_{N_T}^{\prime G},a_{N_T})]\\&\in {\mathbb {R}}^{(N_{T}\times (N^\prime _{u}+1))}, \\ \mathbf {Y^\prime }&= \underline{\varvec{\lambda }}^{\prime L} = [\varvec{\lambda }_1^{\prime L},\varvec{\lambda }_2^{\prime L},...,\varvec{\lambda }_{N_T}^{\prime L}]\in {\mathbb {R}}^{(N_{T}\times N^\prime _{\lambda })}. \\ \end{aligned} \end{aligned}$$

(7)

In this example, the 720-DOF displacement vector ${\varvec{u}}^G$ is compressed into a 4-dimensional vector ($N_{\text{u}^\prime }=4$), which forms a 5-dimensional input combining with crack length parameter in the latent space. Similarly, the 720-DOF reaction force $\varvec{\lambda }^{\prime L}$ is compressed into a 4-dimensional output ($N_{\lambda ^\prime }=4$) in latent space. The GPR-based surrogate models are then built and trained in the designed latent space with training samples $\mathbf {X^\prime }$ and $\mathbf {Y^\prime }$. Since $\mathbf {Y^\prime }\in {\mathbb {R}}^{(N_\text{T}\times N^\prime _{\lambda })}$, GPR surrogate models are constructed for each dimension of $\mathbf {Y^\prime }$ as follows:

$$\begin{aligned} {Y^\prime _i} = {\hat{G}}_i(\mathbf{{X'}}),\;i = 1,\; \ldots ,\;{N'_\lambda }, \end{aligned}$$

(8)

where ${{\hat{G}}_i}( \cdot ), \forall i = 1,\; \ldots ,\;{N'_\lambda }$ is the i-th GPR surrogate model. Note that the surrogate modeling in this paper is not limited to GPR. Because GPR can be computationally inefficient when handling high-dimensional data, the GPR can be replaced by a neural network architecture or other deep learning methods in a case that low-dimensional data can not be accurately generated.

For any given value of $\mathbf {X'}$, we have the prediction from the i-th GPR surrogate model as follows:

$$\begin{aligned} {{\hat{G}}_i}(\mathbf{{X'}})\sim N({\mu _{{Y_i}}},\;\sigma _{{Y_i}}^2), \forall i = 1,\; \ldots ,\;{N'_\lambda } \end{aligned}$$

(9)

in which $N(\cdot )$ is Gaussian distribution, ${\mu _{{Y_i}}}$ and $\sigma _{{Y_i}}$ are, respectively, the mean and standard deviation of the prediction.

Due to the imbalance of the initial training data collected in Sect. 4.1.1, the GPR surrogate models given in Eq. (8) may not accurately represent the original local-domain FE model. Using the GPR surrogate models to replace the original local-domain model in the global–local iterative scheme will lead to large prediction errors due to error accumulation over iterations. To overcome this issue in surrogate model-based IGL algorithm, we present a framework to refine the local-domain surrogate models in the subsequent section.

4.2 Refinement of local-domain surrogate models

An important issue in surrogate modeling is how to achieve a good accuracy with a reasonable number of sample points in the latent space. Due to the error accumulation over iterations as mentioned above, the performance of the surrogate model that replaces the FE process must be carefully calibrated in order to avoid additional system error. As an example shown in Fig. 21, an input that locates in the area with sufficient training points (i.e., well-trained area) will result a low model error when passing the GPR model, while poor-trained area will result a high model error.

Fig. 21

Model error from differently trained regions

Three sequential sampling approaches, i.e., the Maximin approach, Variance Minimization (VM) method, and the Voronoi method are proposed to identify the sample points that need to be trained in the latent space. The goal of this section is to adaptively identify new training points $\mathbf {x}^*$ in the input space, utilizing the information obtained from the existing input space $\mathbf {X}_C$.

4.2.1 Global refinement

The global refinement is defined as a strategy which adds essential points based on current well-trained region to extend the cover range of the latent space. In this case, the Maximin approach (Jin et al. 2002) is adopted which adaptively determines new training points by maximizing the minimum distance between the new point and all current available training points

$$d_{{{\text{new}}}} \, = \,\max \left\{ {\min \left[ {\left\| {d - d^{t} } \right\|_{2} } \right]} \right\},$$

(10)

where $d_\text{new}$ is the identified location of the new training point ${x}^*$, $d^t$ denotes all current available training points, and $\Vert \cdot \Vert _2$ is the $l_2$-norm of a vector. By using this method, a larger training space of the design domain can be evenly sampled with training points.

4.2.2 Local refinement

The local refinement is defined as a strategy which optimizes the training space by further sampling the regions with the largest prediction error. Given the different definitions of “prediction error,” two local refine strategies are developed. In VM method, the new training point in each iteration is selected by minimizing the maximum mean square error (MSE) or prediction variance as

$$d_{{{\text{new}}}} \, = \,\max \{ {\text{MSE}}(d)\} ,$$

(11)

where $\text{MSE}(\cdot )$ is the prediction variance of the surrogate model. The VM methods can effectively construct a global surrogate model when the variation of the response is similar across the design domain. However, VM is limited to the GP-based surrogate modeling method because it requires additional information from model outputs. Besides, when the underlying black box function is highly non-linear in only certain design regions, the VM methods become inefficient (Hu and Mourelatos 2018).

We then further proposed Voronoi method, serving as an alternative to the VM method. The Voronoi method finds the most sensitive Voronoi cell to sample more points in this region. Such sensitive region when removed, the predicted response constructed by the rest of existing points will be far away from the actual response (Xu et al. 2014).

As shown in Fig. 22, the design space is partitioned into $N_C$ Voronoi cells in each iteration, where $N_C$ is the number of training data at current iteration, as follows:

$$\begin{aligned} \Omega = \mathop \cup \limits _{i = 1,...,N_C} {R_i}, \end{aligned}$$

(12)

where $R_i$ is the domain of the $i-th$ cell defined as below:

$$\begin{aligned} {R_i} = \mathop \cap \limits _{{{{\varvec{d}}}_\text{i}} \in {{\varvec{D}}}/{{{\varvec{d}}}_i}} \left\{ {{{\varvec{x}}} \in {{\varvec{X}}},{{\left\| {\mathbf{{x}} - {\mathbf{{d}}_i}} \right\| }_2} \le {{\left\| {\mathbf{{x}} - {\mathbf{{d}}_\text{i}}} \right\| }_2}} \right\} , \end{aligned}$$

(13)

in which ${\mathbf{{D}}/{\mathbf{{d}}_i}}$ represents the training data excluding ${\mathbf{{d}}_i}$.

From the $N_C$ Voronoi cells, the most important cell is identified in each iteration as follows:

$$\begin{aligned} {i^*} = \mathop {\max }\limits _{i \in \{ 1,, \cdots N_C\} } \{e_{LOO}^i\} , \end{aligned}$$

(14)

where $e_\text{LOO}^i$ is the leave-one-out (LOO) prediction bias given by

$$\begin{aligned} e_\text{LOO}^i = \left\| {f({\mathbf{{d}}_i}) - {{{\hat{G}}}_{\mathbf{{D}}/{\mathbf{{d}}_i}}}({\mathbf{{d}}_i})} \right\| , \end{aligned}$$

(15)

in which $f({\mathbf{{d}}_i})$ represents the true response of the training data ${\mathbf{{d}}_i}$ and ${{{\hat{G}}}_{\mathbf{{D}}/{\mathbf{{d}}_i}}}({\mathbf{{d}}_i})$ is the prediction of a GPR model trained using training data $\mathbf{{D}}$ excluding ${\mathbf{{d}}_i}$.

After the important cell (i.e., ${i^*}$) is determined, the new training input is identified in that cell by maximizing the distance between the new training data and the current training data (i.e., ${\mathbf{{d}}_{i^*}}$) as follows:

$$\begin{aligned} {\mathbf{{x}}^*} = \mathop {\arg \max }\limits _{\mathbf{{x}} \in {R_{{i^*}}}} \{ \left\| {\mathbf{{x}} - {\mathbf{{d}}_{{i^*}}}} \right\| \}, \end{aligned}$$

(16)

where $R_i$ is the Voronoi cell defined in Eq. (13).

Once the new training point is added, the design space is then re-partitioned into $N_C+1$ Voronoi cells in the next iteration as illustrated in Fig. 22. Voronoi method takes use of the information from the existing surrogate models and are not limited to the GP-based surrogate modeling method.

Fig. 22

Iteratively adding new training points by the Voronoi method

Fig. 23

Flowchart of the overall procedure from initial surrogate modeling to well-trained model

The overall process of combining global refine and local refine from initial surrogate modeling to well-trained model is shown in Fig. 23. The input space of the GPR is sufficiently sampled by adaptively identifying new training points in the poor-trained region, which improves the surrogate performance without filling the training space blindly. Denoting all the identified new sample point in the input space as ${\varvec{x}}_\text{new}$, to form a complete training dataset for GPR, the corresponding training points in the output space ${\varvec{y}}_\text{new}$ have to be obtained. Firstly, the displacement in physical domain ${{\varvec{u}}_\text{new}^{G}}$ is reconstructed from the compressed displacement ${\varvec{u}}_\text{new}^{\prime G}$ determined in ${\varvec{x}}_\text{new}$. By imposing ${{\varvec{u}}_\text{new}^{G}}$ into the local ABAQUS FE model, the local reaction $\varvec{\lambda }_\text{new}^{L}$ can be solved. The new training point in the output space of GPR model $\varvec{\lambda }_\text{new}^{\prime G}$ is then obtained by compressing the full-dimensional data into latent space using output encoder as follows:

$$\begin{aligned} \begin{aligned}&\text {Decoder}_u={{{\varvec{E}}^\prime }_u}{{\varvec{V}}^\prime }_u^T,\\&\text {Encoder}_\lambda =pseudoinverse({{{\varvec{E}}^\prime }_{\lambda }}{{\varvec{V}}^\prime }_{\lambda }^T), \\&{{\varvec{u}}_\text{new}^{G}}={{\varvec{u}}_\text{new}^{\prime G}} \times \text {Decoder}_u, \\&{\varvec{\lambda }_\text{new}^{\prime L}}={\varvec{\lambda }_\text{new}^{L}} \times \text {Encoder}_\lambda ,\\ \end{aligned} \end{aligned}$$

(17)

The updated training dataset in the latent space of GPR after refinement is now obtained as follows:

$$\begin{gathered} {\mathbf{X}}_{{{\text{updated}}}}^{\prime } = [(u_{1}^{{\prime G}} ,a_{1} ),(u_{2}^{{\prime G}} ,a_{2} ),..., \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(u_{N}^{{\prime G}} ,a_{N} ),(u_{{{\text{new}}}}^{{\prime G}} ,a_{{{\text{new}}}} )] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \in \mathbb{R}^{{((N_{{\text{T}}} + N_{{{\text{new}}}} ) \times (N_{{\text{u}}}^{\prime } + 1))}} , \hfill \\ {\mathbf{Y}}_{{{\text{updated}}}}^{\prime } = [\lambda _{1}^{{\prime L}} ,\lambda _{2}^{{\prime L}} ,...,\lambda _{N}^{{\prime L}} ,\lambda _{{{\text{new}}}}^{{\prime L}} ] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \in \mathbb{R}^{{((N_{{\text{T}}} + N_{{{\text{new}}}} ) \times N_{\lambda }^{\prime } )}} , \hfill \\ \end{gathered}$$

(18)

where $N_\text{new}$ is the total number of added training points in the refinement. The GPR model is then considered as fine-developed as it covers a larger well-trained training region.

4.3 Surrogate IGL method combining statically condensed physics-based model in global domain and data-driven surrogate model in local domain

For the miter gate example, solution of the global domain reduced system of equations (in this example the matrix is $720\times 720)$ takes less than a second. This is particularly attractive when considering the IGL iterations of a non-linear problem. For example, say a crack-propagation is discretized to c crack lengths and each crack length takes 5 IGL iterations. The static condensation reduced matrix can be used 5c times with only one front-end cost, resulting in dramatic time savings.

No special handling is required for the inputs and outputs of the statically condensed global model, making it a plug-in replacement for the FEM global model in IGL as shown in Fig. 24. With these improvements, the bottleneck for IGL solution time is now the local problem. However, while calculating ${\varvec{p}}_\text{i}$ the reaction forces of $\Omega _\text{GA}$ cannot be pulled directly from the FEM model without element information around the boundary, so the statically condensed global auxiliary domain is used instead.

Fig. 24

Illustrated IGL algorithm for miter gate with (1) global and global auxiliary static condensation uncondensed nodes and (2) local-domain mesh discretization

The proposed surrogate local model in Sect. 4 removes the local solution bottleneck. The GPR surrogate local model receives ${\varvec{u}}_i^G$ and outputs $\varvec{\lambda }_i^L$, making it a plug-in replacement for the FEM local model. The surrogate iterative global–local method is illustrated in Fig. 25.

Fig. 25

Illustrated surrogate IGL algorithm for miter gate with (1) global and global auxiliary static condensation uncondensed nodes and (2) local-domain GPR surrogate

4.4 Extracting SIF values after convergence

After the IGL reaches its convergence, the local FE model after the last iteration is considered to preserve a true physics. As mentioned above, the SIF value at the middle node through the thickness of the is extracted from the local model after post-processing. In SIGL, however, due to the physics is replaced by surrogate modeling, it is important to fill the gap between local reaction forces ${\lambda }_\text{convergence}^L$ and SIF. Given that, another surrogate model is built and trained to increase the running efficiency.

In this case, the 720-DOF reaction force vector $\varvec{\lambda }_\text{i}^L$ is compressed into a 4-dimensional vector, which forms a 5-dimensional input combining with crack length parameter in the latent space. The output is then defined as the desired SIF value $K_{1-SIGL}$. The GPR-based surrogate models are then built and trained in the designed latent space with training samples ${\varvec{X}}$ and $K_{1-SIGL}$.

$$\begin{aligned} {K_{1-SIGL}} = G_{SIF}(\mathbf{{X}}), \end{aligned}$$

(19)

where $G_\text{SFIF}( \cdot )$ is the GPR surrogate model connecting local reaction forces with SIF.

For any given value of local reaction forces $\mathbf {X}$, we have the prediction of SIF from the GPR surrogate model as follows:

$$\begin{aligned} {G_\text{SIF}}(\mathbf{{X}})\sim N({\mu _\text{{K}}},\;\sigma _\text{K}^2), \end{aligned}$$

(20)

in which $N(\cdot )$ is Gaussian distribution, ${\mu _\text{K}}$ and $\sigma _\text{K}$ are, respectively, the mean and standard deviation of the SIF prediction.

Next, we will use the miter gate example presented in Sect. 3 to compare the different approaches including submodeling, IGL, and surrogate-based IGL (SIGL).

5 Results and discussion

Several solution methods have been covered: (1) Reference tying method, (2) submodeling, (3) IGL, (4) IGL with static condensation for global and auxiliary domains, and (4) SIGL. The methods for which accuracy is considered in this research are the IGL and SIGL methods. An example of their accuracy with a miter gate and $a=1$ in, $h_\text{up}=50$ ft, $h_\text{down}=16$ ft, and $l_\text{dmg}=0.5$ in is shown in Fig. 26. The IGL method with and without static condensation gives the same solution, so it is not shown in the figure.

Fig. 26

Error convergence of IGL and SIGL methods for $a=1$ in, $h_\text{up}=50$ ft, $h_\text{down}=16$ ft, and $l_\text{dmg}=0.5$ in

For the IGL method, the error drops below $10^{-5}$ after only three iterations. The SIGL method takes more iterations, but reaches an error below $10^{-4}$. While the error definition in Algorithm 1 is convenient for defining the IGL method convergence, the example problem proposed depends on the accuracy of the stress intensity factors along the crack front as compared with the reference tying method. Figure 27 shows the relative stress intensity factor error $e_K$ evaluated at each IGL method and SIGL method iteration.

Fig. 27

SIF error $e_K$ convergence of IGL and SIGL methods for $a=1$ in, $h_\text{up}=50$ ft, $h_\text{down}=16$ ft, and $l_\text{dmg}=0.5$ in

The IGL method quickly converges to below $10^{-3}$ while the SIGL method lags somewhat, but still achieves an $e_K$ near $2\%$. Since the residual convergence e showed better convergence, it seems likely that this is due to lack of accuracy in the SIF surrogate model. As for the higher $e_K$ than e, it can be helpful to look at the physical quantities each deal with. The error e deals with residual forces at nodes, quantities solved for directly in the system of equations. However, $e_K$ depends on contour integrals involving evaluation of stress, a derived quantity from the displacements. Therefore, the error will be higher for SIF outputs than for residual forces. However, the SIF error stagnates at around $4\times 10^{-4}$. This may be due to computer precision error between the reference tied model definition and IGL model definition, e.g., the geometry in Abaqus seems to only have single precision. Figure 28 shows the SIF error $e_K$ accuracy of the converged IGL and SIGL compared with the submodeling solution.

Fig. 28

SIF error $e_K$ accuracy of submodeling, IGL and SIGL methods for $a=1$ in, $h_\text{up}=50$ ft, $h_\text{down}=16$ ft, and $l_\text{dmg}=0.5$ in

It can be seen that while $e_K$ is similar for submodeling and the SIGL method, e is much smaller for the SIGL method. Since the IGL method is much more accurate than the submodeling model, this points to room for improvement in the surrogate SIF model. Also, the crack length is very small ($a\,=\,1$), helping the submodeling St. Venant’s assumption hold. As the crack length grows, the submodeling solution will become much less accurate. The SIGL method accuracy for varying a and $l_\text{dmg}$ will be explored later in this section. For now, Fig. 29 shows the time to solution for several methods on the same desktop computer using 2 processors (CPUs) with a RAM of 32 GB.

Fig. 29

Solution time for reference tying model, submodeling, IGL, IGL with global and auxiliary static condensation, and SIGL methods for $a=1$ in, $h_\text{up}=50$ ft, $h_\text{down}=16$ ft, and $l_\text{dmg}=0.5$ in

The reference solution takes about 150 s. Interestingly, the submodeling solution takes longer than the reference solution, which bodes ill for the IGL method. A possible explanation for this may be inefficiencies in multiple Abaqus calls versus one in input file analysis, assembly, solution, and post-processing. The IGL method takes three iterations and about three times the time of the reference solution. Using static condensation on the global and auxiliary problems cuts the IGL solution time in half, but IGL with static condensation is still slower than the reference solution. This is surprising given some of the discussion in Sect. 2.2 claiming a potential speed advantage for IGL. However, this can be explained by the limitations of performing analysis with Abaqus. Abaqus does not store the factorized stiffness matrix between jobs, so every job called after the first IGL iteration requires an (unnecessary to IGL) stiffness matrix assembly and factorization. However, The SIGL method has such a small time to solution 1.06 s that the bar is not visible.

Figure 30 shows the reference SIF results over cracks from 0.5 to 4.0 in and damage gap height from 10 to 150 in. The SIF values get higher for longer cracks, but the behavior for higher damage gaps is more complicated. In the range of 60–120 in the SIF values are actually smaller, showing the importance of the location of the crack on the miter gate. Since the damage gap is at the bottom of the gate, the load path travels up and around it, and coincidentally the crack as well. However, the pintle (bottom hinge support) can take load, so as the damage gap grows higher the load paths somewhat divert back down through the crack.

Fig. 30

Heatmap of SIFs for reference solution in ksi$\sqrt{\text {in}}$

Figure 31 shows the ability of the surrogate iterative global–local method to model the miter gate. Interestingly, globally refining the surrogate local model leads to overestimation of the SIF value for large damage gaps. Considering that local refinement improves the solution drastically, the solution must be very sensitive for large damage gap heights. In fact, looking at the residual map for global refine, the error clearly depends on damage gap height more than crack length, peaking at the extremes. Higher errors are near the edges. Both local refine methods manage to control the prediction error based on the global refine improvement.

Fig. 31

SIF heatmaps showing SIGL performance in ksi$\sqrt{\text {in}}$

6 Conclusion

A surrogate iterative global–local methodology has been proposed to reduce computation time for problems with cracked large steel structures. This research novelly represents the local domain in an IGL problem using a surrogate model rather than a physics-based model. It was shown that for the example problem (with a linear local domain) IGL was extremely accurate, while the required computational cost is high which is not suitable for probabilistic analysis such as failure diagnostics under the Bayesian framework. However, SIGL achieves acceptable accuracy and is extremely fast. This makes SIGL well suited for diagnosis and prognostic tasks in digital twins.

Future research will look at handling non-linear global problems and utilization of SIGL to probabilistically infer crack length given sensor readings.