Layout optimization of long-span structures subject to self-weight and multiple load-cases

Abstract

Layout optimization provides a powerful means of identifying materially efficient structures. It has the potential to be particularly valuable when long-span structures are involved, since self-weight represents a significant proportion of the overall loading. However, previously proposed numerical layout optimization methods neglect or make non-conservative approximations in their modelling of self-weight and/or multiple load-cases. Combining these effects presents challenges that are not encountered when they are considered separately. In this paper, three formulations are presented to address this. One formulation makes use of equal stress catenary elements, whilst the other two make use of elements with bending resistance. Strengths and weaknesses of each formulation are discussed. Finally, an approach that combines formulations is proposed to more closely model real-world behaviour and to reduce computational expense. The efficacy of this approach is demonstrated through application to a number of 2D- and 3D-structural design problems.

1 Introduction

In very long-span structures the weight of the structure itself is often the dominant source of loading (Brancaleoni et al. 2011), making it imperative that these structures are as lightweight as possible. Structural optimization therefore has the potential to provide substantial benefits. However, in this case it is important that the self-weight loading is modelled accurately, to prevent misleading indications of optimality.

Widely used continuum topology optimization methods (e.g. Bendsoe and Sigmund 2003; Wang et al. 2003; Sigmund and Maute 2013) are not well suited to long-span structures. This is because a typical long-span bridge problem may include a design domain that is several kilometres in length, but structural elements that are of the order of centimetres in cross-section. Tackling such problems would require the use of very high resolutions when using continuum methods. For example, significant computational resources (up to 85 h of runtime on 16,000 CPU cores) were required by Baandrup et al. (2020) to solve a problem representing a small portion ($\frac{1}{62}$ of the bridge length) of the deck of a long-span bridge. This generated a form that was primarily skeletal in nature, with regions of shell-like structure, further suggesting that a frame based optimization approach is likely to be more appropriate for such an application.

Discrete layout optimization methods can be used to obtain optimal structures consisting of individual elements (e.g. truss bars). This not only avoids difficulties in modelling relatively small elements, but is also well suited to structures whose scale requires that they be assembled from many smaller components. The most common optimization approach for trusses is the ground structure-based layout optimization method (also sometimes referred to as the ‘truss topology optimization’ method), originally proposed by Dorn et al. (1964). The efficiency of this method was improved by Gilbert and Tyas (2003), who implemented an adaptive ‘member adding’ method, taking advantage of the column generation mathematical programming procedure (Gilmore and Gomory 1961; Lübbecke and Desrosiers 2005). This allows problems with very high resolution to be solved, whilst keeping run times and memory usage acceptable. The visual clarity of the solutions obtained can be improved by adjusting the nodal positions using a geometry optimization rationalization step (He and Gilbert 2015).

Bridge-like structures have been previously studied using truss optimization approaches, as well as using analytical methods to directly address the Michell-Hemp optimality criteria (Michell 1904; Hemp 1978). However, in previous studies the self-weight of the structure is not generally considered, and so the results are applicable only to shorter spans.

Hemp (1974) proposed a solution to a single-span problem involving transmission of a distributed load to a pair of pinned supports, sometimes referred to as the ‘Hemp arch’ problem. This solution was shown to be optimal for non-uniform loading (Chan 1975), or unequal tension and compression strengths (Pichugin et al. 2012), although it is slightly sub-optimal for the problem originally posed. Sokół and Rozvany (2013) considered an extension of this to a multiple load-case problem.

Problems with infinitely many spans have been considered by Pichugin et al. (2015), Beghini and Baker (2015) and Fairclough et al. (2018). To date there appear to have been only a few cases of established structural optimization concepts being used by practising engineers to inspire real-world bridge designs (Graczykowski and Lewinski 2020), with issues such as lack of consideration of self-weight meaning that these have not been directly applicable to long-span structures.

Where self-weight has been considered within a numerical, ground structure-based, layout optimization process, it has almost universally been assumed that the weight of a member may be taken to act directly upon its end points (Bendsøe et al. 1994; Pritchard et al. 2005; Kanno 2012). This approach is appealing as it is conceptually simple and can be implemented without difficulty (no new variables or constraints are required in the layout optimization problem). However, as will become clear, this approach can give rise to unrealistic and non-conservative solutions, especially when the self-weight loading is significant. For example, Kanno and Yamada (2017) noted that this approach has a tendency to produce optimal structures with overlapping structural elements. They proposed an approach using mixed integer programming to directly prevent this. Whilst this was effective at addressing the overlapping members, the existence of these members is merely a symptom of a larger underlying problem; the lumped mass approach introduces intrinsic non-conservative errors and the presence of excessively long elements is simply a manifestation of this.

Allowance for self-weight in analytical solutions was considered by Rozvany and Wang (1984), who proposed a modified form of the Prager-Shield optimality criteria. It can be shown that the lumped mass formulation tends towards an identical constraint only as the length of members tends to zero. Perhaps a more intuitive explanation of this effect is to consider the bending stresses that would be generated by self-weight when it is applied as a distributed load along the element. These bending stresses are neglected by the lumped mass approach.

Fairclough et al. (2018, 2022) developed an alternative approach involving the use of ‘catenary’ elements, which addresses the underlying issue by using elements which have the shape of a catenary of equal stress. This shape is defined by the presence of only axial stresses under the combined action of self-weight and axial load, and therefore avoids the issue of bending stresses mentioned previously. However, this approach is only applicable to problems involving a single load-case, whereas in the present contribution the goal is to extend this approach to scenarios involving multiple load-cases.

An alternative means of resisting the bending action generated by self-weight is to use members explicitly possessing the required bending resistance. Pure bending structures have been widely studied in the context of beam grillage layout optimization (Rozvany 1972; Hill and Rozvany 1985; Bolbotowski et al. 2018). In this application the bending resistance of an element is linked by a linear relationship to the cross-sectional area; this can be achieved in practice by seeking the width of a cross-section of given (fixed) depth. Numerically, this leads to a linear optimization problem (Bolbotowski et al. 2018), which is quick to solve and for which globally optimal solutions can be obtained, whereas altering both width and depth leads to a more complex non-convex problem. It is usual to neglect the influence of shear stresses generated by the bending, although Rozvany (1979) does consider a case where the area of an element is given by a linear expression involving the magnitudes of both the applied moment and shear force.

The nature of the Michell-Hemp criteria is such that when both axial and bending actions are permitted, solutions involving the use of just axial elements will generally be favoured. Nonetheless, some practical applications have prompted activity in this area.

It has been found that the resulting non-convex problems can be solved effectively using gradient methods, such as the method of moving asymptotes (Pedersen 2003), and sequential conic programming (Lu et al. 2022). Alternatively meta-heuristic methods that are unaffected by the convexity or otherwise of the problem have been widely applied to such problems (Liu et al. 2012; An and Huang 2017), though the optimality of the solutions obtained is uncertain. Additionally, formulations that involve picking catalogue cross-sections have been used by Kureta and Kanno (2014), Van Mellaert et al. (2018), and Brütting et al. (2020). In this case integer programming methods must be employed (Grossmann et al. 1992), allowing optimal solutions to be obtained, albeit usually at high computational cost. Pre-existing frame elements have also been considered in truss optimization formulations (Liang et al. 2000; Lu et al. 2018); however, in these problems the element dimensions are fixed and only the internal forces are subject to optimization, thus avoiding the need for non-convex constraints.

In this paper the focus is on developing computationally efficient means of solving layout optimization problems involving multiple load cases in the presence of self-weight, overcoming limitations associated with previously proposed methods. The paper focuses on the case where the goal is to minimize the volume of a structure comprising a rigid-plastic material of given strength. Also, the aim is to develop a computationally efficient formulation that is potentially suitable for use in practice. As such, various approximations are required, though these are chosen so as to be conservative (i.e. to lead to overestimations in the volume of material required), to ensure the results obtained are practically useful.

The paper is structured as follows: in Sect. 2 formulations that can be used to model self-weight within a layout optimization model are described, including both existing and novel approaches. In Sect. 3 these approaches are compared for problems involving individual elements and small-scale structures. In Sect. 4 a means of combining formulations from Sect. 2 to enable practical problems to be solved in a computationally efficient manner is discussed. The resulting combined approach is then applied to a range of problems of practical interest in Sect. 5. Finally concluding remarks are presented in Sect. 6.

2 Problem formulations

In this section, a number of layout optimization formulations are presented. Section 2.1 describes the standard formulation in which self-weight is neglected. Various methods of handling self-weight are then presented. Specifically, in Sect. 2.2, the lumped mass approach is recalled; in Sect. 2.3 the catenary element approach is described and then extended to now enable multiple load-cases to be handled; in Sects. 2.4 and 2.5 the self-weight of an element is assumed to be carried via bending action, assuming respectively rigid (moment-resisting) and pinned end connections.

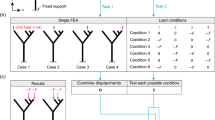
Each of the aforementioned formulations can be handled using the standard ground structure layout optimization method, as shown in Fig. 1. Thus the problem is defined in terms of a design domain, supports, and applied loads (Fig. 1a), where the latter can be applied simultaneously (single load-case) or separately (multiple load-cases). The domain is discretized with nodes (Fig. 1b), which are connected with potential members (Fig. 1c). Here, the adaptive member adding approach proposed by Gilbert and Tyas (2003) is used, with adjacent connectivity employed for the initial ground structure. Finally, the optimization problem is formulated and solved to obtain the optimized minimum volume structure; when only a single load case is involved this may be in unstable equilibrium with the applied loads, as in Fig. 1d.

Static (equilibrium) formulations are presented here, but solutions for the kinematic (dual) problem are available through the use in this case of the MOSEK Aps (2020) primal-dual interior point solver.

Fig. 1

Layout optimization procedure: a definition of domain, loads and supports; b discretization of domain using nodes; c ground structure containing all potential members; d minimum volume solution (single load-case)

2.1 Weightless formulation

The plastic truss layout optimization formulation for a truss comprising n nodes and m weightless members may be stated as follows:

$$\begin{aligned} \min _{\mathbf {a}, \mathbf {q}_k} V&= \mathbf {l}^{\text T} \mathbf {a} \end{aligned}$$

(1a)

$$\begin{aligned} \text { subject to } (\mathbf {Bq}_k&= \mathbf {f}_k )_{\forall k} \end{aligned}$$

(1b)

$$\begin{aligned} (\mathbf {q}_k&\le {\sigma}_{\text{T}} )_{\forall k} \end{aligned}$$

(1c)

$$\begin{aligned} (-\mathbf {q}_k&\le {\sigma}_{\text{C}})_{\forall k} \end{aligned}$$

(1d)

$$\begin{aligned} \mathbf {a}&\ge \mathbf {0} \end{aligned}$$

(1e)

where the objective V is the total volume of the structure, calculated using $\mathbf {l} = [l_1, l_2,\ldots , l_m]$, a vector containing the length of each member, and $\mathbf {a} = [a_1, a_2,\ldots , a_m]$, a vector containing optimization variables which represent the cross-sectional areas of each member.

Constraint (1b) enforces equilibrium in each Cartesian direction at each node; this constraint is applied separately in each load-case, k. Also $\mathbf {q}_k = [q_{1,k}, q_{2,k},\ldots , q_{m,k}]$ contains optimization variables representing the axial force in each member in load-case k. For a two dimensional problem, $\mathbf {f}_k = [f_{1,k}^x, f_{1,k}^y, f_{2,k}^x,\ldots , f_{n,k}^y]$ is a vector containing the externally applied forces at each node in load-case k (for a three-dimensional problem, $f^z$ components must also be included). Where there are supported degrees of freedom, either the reaction force may be explicitly treated as an optimization variable or, as is the case herein, the relevant constraint may be removed. Finally, $\mathbf {B}$ is a $2n \times m$ (or, in three dimensions, $3n \times m$) matrix of direction cosines, such that the contribution of a single element i connecting nodes A and B may be written as:

$$\begin{aligned} \begin{bmatrix} -\cos \theta \\ -\sin \theta \\ \cos \theta \\ \sin \theta \end{bmatrix} \begin{bmatrix} q_{i,k} \end{bmatrix} =\begin{bmatrix} f^x_{\mathrm{A},k} \\ f^y_{\mathrm{A},k} \\ f^x_{\mathrm{B},k} \\ f^y_{\mathrm{B},k} \end{bmatrix} \end{aligned}$$

(2)

where $\theta$ is the angle between the element centreline and the positive x direction.

Finally, Eqs. (1c) and (1d) are strength or ‘yield’ constraints, with ${\sigma}_{\text{T}}$ and ${\sigma}_{\text{C}}$ being the limiting stresses in tension and compression, respectively.

2.2 Lumped formulation

In the standard lumped mass formulation the weight of an element is assumed to act directly on its end points. Considering the weightless formulation, only the equilibrium constraint Eq. (1b) needs to be changed to now include an additional term relating to the area of each member. Thus the contribution of a single element i to the equilibrium constraints changes from Eq. (2) to become:

$$\begin{aligned} \begin{bmatrix} -\cos \theta \\ -\sin \theta \\ \cos \theta \\ \sin \theta \end{bmatrix} \begin{bmatrix} q_{i,k} \end{bmatrix} +\begin{bmatrix} 0 \\ -\frac{\rho g l_i}{2} \\ 0 \\ -\frac{\rho g l_i}{2} \end{bmatrix} \begin{bmatrix} a_i \end{bmatrix} =\begin{bmatrix} f^x_{\mathrm{A},k} \\ f^y_{\mathrm{A},k} \\ f^x_{\mathrm{B},k} \\ f^y_{\mathrm{B},k} \end{bmatrix} \end{aligned}$$

(3)

where $\rho$ is the density of the material, g is the acceleration due to gravity (which is assumed to act in the negative y direction) and $l_i$ is the length of the member.

2.3 Catenary formulation

Fig. 2

Equal stress catenary element (single load-case): a form of element, showing end forces aligned to centre-line of element; b straight-line force transmission with lumped masses. The light and dark grey shaded areas in a correspond to the light and dark grey lumped masses in b

The formulation outlined here employs the equal stress catenary elements described by Fairclough et al. (2018) for single load-case layout optimization problems; in this section the approach is extended to consider multiple load-cases. These elements have a curved centreline, arching upwards when under compression, and sagging downwards when under tension; in the optimization it is convenient to treat tensile and compressive elements as separate elements interlinking a given pair of nodes. However, in the interests of clarity an element carrying a tensile force (only) is considered in the following, as shown in Fig. 2a, and the subscript i (as used in Eqs. (2) and (3)) is also omitted.

2.3.1 Equilibrium

Before considering multiple load-case scenarios, an alternative— but equivalent—perspective on the single load-case formulation will be discussed. This model is shown in Fig. 2b, where the notional axial force q is separated from the self-weight forces W.

From Fairclough et al. (2018, Eq. (2.8)):

$$\begin{aligned} W_{\text{PQ}} = \rho g V_{\text{PQ}} = -q_x(\tan \alpha _{\text{Q}} -\tan \alpha _{\mathrm{P}}) \end{aligned}$$

(4)

where $W_{\text{PQ}}$ and $V_{\text{PQ}}$ are the weight and volume of the section of catenary between P and Q, and $q_x$ is the horizontal component of the force in the element. Note that $q_x$ is constant at all points along the catenary, and is equal to $q\cos \theta$, where $\theta$ is as defined in Fig 2b. Also, $\alpha$ is the angle between the catenary centreline and the positive x axis at the subscripted point; see Fairclough et al. (2018) for details of how this is calculated.

The point M (shown in Fig. 2) is defined as the point at which the tangent to the element’s centreline is parallel to the straight line AB, i.e. $\alpha _{\text{M}} = \theta$. Point M is the dividing point when considering the catenary as a lumped mass, i.e. the weight of the section AM is applied at point A, and the weight of section MB is applied at point B. The weight of section AM can be calculated from Eq. (4) as follows:

$$\begin{aligned} W_{\text{AM}}&= -q\cos \theta (\tan \theta - \tan \alpha _{\text{A}})\nonumber \\&= -q(\sin \theta - \cos \theta \tan \alpha _{\text{A}}) \end{aligned}$$

(5)

The external force q is directed along the straight line AB, as shown in Fig. 2b. It is evident that the horizontal component is identical to that shown in Fig. 2a. It can also be seen that the total vertical load at A is $-W_{\text{AM}} - q\sin \theta$, which may be simplified using Eq. (5) to compute $W_{\text{AM}}$. Thus:

$$\begin{aligned} q_{y,{\text A}}&= q(\sin \theta - \cos \theta \tan \alpha _{\text{A}}) - q\sin \theta \nonumber \\&= -q\cos \theta \tan \alpha _{\text A} \end{aligned}$$

(6)

Similar logic may be used to confirm the forces at point B. Thus, the representation shown in Fig. 2b is fully equivalent to the one in Fig. 2a for single load-case problems. Significantly, from the representation presented in Fig. 2b, it is easy to see how equilibrium equations for other load-cases can be established when the weights $W_{\text{AM}}$ and $W_{\text{MB}}$ are constant and only the axial force q varies.

For the multiple load case formulation, r can be defined as the maximum value of q, from which the required cross-sectional area of the element can be calculated. Thus:

$$\begin{aligned} W_{\text{AM}} = -r(\sin \theta - \cos \theta \tan \alpha _{\text{A}}) \end{aligned}$$

(7)

In each load-case k, the element force is given by $q_k$, so that the required equilibrium constraint becomes:

$$\begin{aligned} \begin{bmatrix} 0 \\ \cos \theta \tan \alpha _{\mathrm{A}} - \sin \theta \\ 0 \\ \sin \theta -\cos \theta \tan \alpha _{\mathrm{B}} \end{bmatrix} r + \begin{bmatrix} \cos \theta \\ \sin \theta \\ -\cos \theta \\ -\sin \theta \end{bmatrix} q_k =\begin{bmatrix} f^x_{{\text A},k}\\ f^y_{{\text A},k}\\ f^x_{{\text B},k}\\ f^y_{{\text B},k}\\ \end{bmatrix} \end{aligned}$$

(8)

However to provide easier comparison with the single load-case formulation, and in the interests of numerical stability, it is convenient to use the value of $r-q_k$ as the optimization variable, denoted as $p_k$. Thus the equilibrium constraint becomes:

$$\begin{aligned} \begin{bmatrix} \cos \theta \\ \cos \theta \tan \alpha _{\text {A}} \\ -\cos \theta \\ -\cos \theta \tan \alpha _{\text {B}} \end{bmatrix} r + \begin{bmatrix} -\cos \theta \\ -\sin \theta \\ \cos \theta \\ \sin \theta \end{bmatrix} p_k =\begin{bmatrix} f^x_{\text {A},k}\\ f^y_{\text {A},k}\\ f^x_{\text {B},k}\\ f^y_{\text {B},k}\\ \end{bmatrix} \end{aligned}$$

(9)

Fig. 3

Conceptual model of catenary element loaded at approximately half capacity ($q_k = 0.5r$). The black region is considered to be fully stressed (and is equal to a catenary element where the maximum design load is equal to $q_k$), whilst the dark and light grey shaded regions are considered unstressed and are applied as lumped masses at points A and B, respectively

This also means that the coefficients of r are the same as in the single load-case formulation, so that the limits for vertical elements given by Fairclough et al. (2022) may also be used. (Note also that there are no difficulties in directly calculating the coefficients of $p_k$ for the case $\theta = 90^\circ$.)

2.3.2 Yield conditions

Here, a simplified yield constraint based on the lumped mass approach will be used. The yield conditions in this case may be imposed by first conceptualizing a given element as in Fig. 3, where a core in the centre of the element is considered as a fully stressed catenary, and additional material located at the edges of the section is assumed to be lumped at element end-points.

For this simplified yield condition, the required optimization constraint is simply that the stressed core of the catenary takes between 0% and 100% of the total cross-section, i.e. that $0\le q_k \le r$. To re-write this using the preferred optimization variable gives:

$$\begin{aligned} r \ge p_k \ge 0 \end{aligned}$$

(10)

Note that when $p_k = 0$ (i.e. the element is fully utilized), this simplified yield condition precisely reproduces that present in the single load-case formulation. As the utilization is reduced, some error is introduced by the assumption that unused material can be transmitted to the nodes at no additional cost, similar to the formulation in Sect. 2.2. In reality, as soon as the axial load, $q_k$ on an element is reduced from its maximum value r, the internal equilibrium state involving purely axial stresses no longer holds, and bending moments are generated within the element.

It will be shown in Sect. 4 that this simplified approach is well suited to modelling the situation in the cables found in real-world cable-supported bridge structures. Also, even for other cases, this formulation provides an improvement over the lumped mass approach; the catenary element is capable of withstanding the internal effects of self-weight in, at least, the fully loaded case.

2.3.3 Volume

For this approach, the volume of the element is no longer simply defined as $l_i a_i$ as in Eq. (1a). Instead the volumes are calculated as in Eq. (3.4) of Fairclough et al. (2018), although now using the defining force r to give:

$$\begin{aligned} V_i = r \frac{\cos \theta _i}{\rho g} (\tan \alpha _{\text {A}} -\tan \alpha _{\mathrm{B}}) \end{aligned}$$

(11)

Fig. 4

Nodal forces and moments acting on a beam element AB, where the element weight acts as a uniformly distributed downwards vertical load. Key geometric parameters are also indicated

2.4 Beam formulation 1: rigid joints

The next two formulations are based on the use of beam elements, i.e. elements where the self-weight is applied continuously along a straight, prismatic element, which is capable of carrying the induced bending stresses. As the elements are assumed to be prismatic, the volume can be calculated in the same way as in Eq. (1a).

In this section, it will be assumed that the connections between adjacent members are capable of transmitting moments; Sect. 2.5 will consider the case where these connections are pinned. Again, subscript i is omitted for sake of clarity.

2.4.1 Equilibrium

The optimization variables here are the area, a, and, for each load-case k, the end moments $m_{\text{A},k}, m_{\text{B},k}$ and the notional axial force $q_k$ (defined as the axial force at the mid-point). The self-weight produces a uniformly distributed load with total magnitude $W = \rho g a l$, where l is the member length as shown in Fig. 4. End forces, $v_{\text{A}}, v_{\text{B}}$ and $q_{\text{A}}, q_{\text{B}}$ (Fig. 4), are found using equilibrium of the element, giving the values shown in Fig. 7. Thus the equilibrium equations in global coordinates are:

$$\begin{aligned} \begin{bmatrix} -\cos \theta &{}\quad -\frac{\sin \theta }{l}&{}\quad -\frac{\sin \theta }{l}\\ -\sin \theta &{}\quad \frac{\cos \theta }{l} &{}\quad \frac{\cos \theta }{l}\\ 0 &{}\quad 1 &{}\quad 0\\ \cos \theta &{}\quad \frac{\sin \theta }{l}&{}\quad \frac{\sin \theta }{l} \\ \sin \theta &{}\quad -\frac{\cos \theta }{l} &{}\quad -\frac{\cos \theta }{l}\\ 0 &{}\quad 0 &{}\quad 1 \end{bmatrix} \begin{bmatrix} q_k \\ m_{\mathrm{A},k} \\ m_{\mathrm{B},k} \end{bmatrix} + \begin{bmatrix} 0 \\ -\frac{\rho g l}{2} \\ 0 \\ 0 \\ -\frac{\rho g l}{2} \\ 0 \end{bmatrix} a = \begin{bmatrix} f_{{\text A},k}^x\\ f_{{\text A},k}^y\\ M_{{\text A},k}\\ f_{{\text B},k}^x\\ f_{{\text B},k}^y\\ M_{{\text B}, k} \end{bmatrix} \end{aligned}$$

(12)

where e.g. $f_{\text {A}}^x, f_{\text {A}}^y$ are the forces in the x and y directions at A, and $M_{\text {A}}$ is the total moment transmitted at A.

2.4.2 Yield constraints

For the purposes of calculating the yield constraints, the cross-section of the member will be split into two regions, with areas $a_{{N}}$ and $a_{{M}}$, following the approach proposed by Lu et al. (2022). A region of area $a_{{N}}$ carries the axial and shear forces acting on the element, with regions of total area $a_{{M}}$ carrying the axial stresses generated by the applied moments, as shown in Fig. 5.

This split may be different in each load-case, but in all cases the sum of the two areas must not be greater than the total area a, giving the following constraint:

$$\begin{aligned} a_{{N},k} + a_{{M}, k} \le a \end{aligned}$$

(13)

The yield constraints for the two regions will be considered separately.

Moment yield The region with area $a_{{M}}$ is divided into two equal areas, which occupy the top and bottom of the cross-section, as shown in Fig. 5a. The plastic moment capacity of this region is given by the expression $\frac{\sigma d}{2} a_{{M}}$, where $\sigma$ is the limiting stress of the material, and d is the distance between the centroids of the two halves of the $a_{{M}}$ region.

Fig. 5

Cross-sections with fixed bending depth d: a scenario with low value of axial loading and highest value of bending moment; b scenario with high axial loading and lower applied moment

The moment yield constraints at the end-points A and B are given by:

$$\begin{aligned} \left[ \begin{array}{cc} 1 &{}\quad 0 \\ -1 &{}\quad 0 \\ 0 &{}\quad -1 \\ 0 &{}\quad 1 \end{array}\right] \left[ \begin{array}{c} m_{\mathrm{A}, k} \\ m_{\mathrm{B}, k} \end{array}\right] \le \frac{\sigma d}{2} \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}\right] \begin{bmatrix} a_{{M}, k} \end{bmatrix} \end{aligned}$$

(14)

This constraint is linear and convex only if d is constant; therefore the value of d must be pre-defined. Note that this may give a slight, conservative, error in the bending resistance for cases when an element carries less moment loading, as shown in Fig. 5b.

Fig. 6

Bending moment diagrams for a beam element with and without self-weight effects

When self-weight is considered, an additional parabolic distribution is added to the bending moment diagram; this is shown in the filled diagram on Fig. 6. The maximum absolute value of bending moment may now occur at any point along the beam, which is problematic in a layout optimization context. Thus a conservative piecewise linear approximation of the curve can be used, constructed from tangents to the curve located at mid- and end-points of the beam. With this representation the peak bending moment can occur only at the end-points, or at the transition points between piecewise linear elements, i.e. at beam quarter points.

The maximum bending moment contribution from self-weight, $M_{\mathrm{sw}}$, occurs at the midpoint of the parabolic distribution, and also at the quarter points of the approximated distribution. It is calculated based on the total element weight, distributed over a horizontal span $\bar{x} = x_{\text{B}} - x_{\text{A}}$, thus:

$$\begin{aligned} M_{\mathrm{sw}} = \frac{1}{8} \rho g l | \overline{x}| a \end{aligned}$$

(15)

Therefore expressions can be formulated with sagging moments as positive. When point A is to the left of point B (i.e. $\bar{x}$ is positive) the relevant expression is:

$$\begin{aligned} \begin{bmatrix} -0.25 &{}\quad 0.75 \\ -0.75 &{}\quad 0.25 \end{bmatrix} \begin{bmatrix} m_{{\text A},k} \\ m_{{\text B},k} \end{bmatrix} +\frac{\rho g \bar{x} l}{8} \begin{bmatrix} 1 \\ 1 \end{bmatrix} a \le \frac{\sigma d}{2} \begin{bmatrix} 1 \\ 1 \end{bmatrix} a_{{M},k} \end{aligned}$$

(16)

and when point B is to the left of point A (i.e. $\bar{x}$ is negative):

$$\begin{aligned} \begin{bmatrix} 0.25 &{}\quad -0.75 \\ 0.75 &{}\quad -0.25 \end{bmatrix} \begin{bmatrix} m_{{\text A},k} \\ m_{{\text B}, k} \end{bmatrix} + \frac{\rho g \bar{x} l}{8} \begin{bmatrix} -1 \\ -1 \end{bmatrix} a \le \frac{\sigma d}{2} \begin{bmatrix} 1 \\ 1 \end{bmatrix} a_{{M},k} \end{aligned}$$

(17)

Both (16) and (17) may be applied to all elements; if the sign of $\bar{x}$ is opposite from that mentioned, then those constraints will become less critical than (14), and so do not affect the solution. This becomes essential when movement of nodes may cause an element to change direction, for example if the method is extended to permit geometry optimization (He and Gilbert 2015).

Fig. 7

Force distributions along a beam element: a normal force; b shear force. Dashed lines show distribution in the case where self-weight is neglected, solid lines show case where self-weight is considered

Axial yield The region of the beam with area $a_N$ is assumed to carry both axial and shear loading. When self-weight is neglected, both axial and shear forces are constant, having values of q and $\frac{m_{\text {A}} + m_{\text {B}}}{l}$ respectively, as shown by dashed lines in Fig. 7.

However, when self-weight is considered, the distributions of normal and shear force are linear, as shown in Fig. 7. It will be (conservatively) assumed that the worst case for shear and normal forces are co-incident. For convenience here variables $q_\text N$, to be the largest absolute value of the normal force, and $q_\text V$, to be the largest absolute value of the shear force, are defined using the following constraints:

$$\begin{aligned}&\left[ \begin{array}{c} 1 \\ 1 \\ -1 \\ -1 \end{array}\right] q_k + \frac{\rho gl}{2} \sin \theta \left[ \begin{array}{c} 1 \\ -1 \\ 1 \\ -1 \end{array}\right] a&\le \left[ \begin{array}{c} 1\\ 1 \\ 1 \\ 1 \end{array}\right] q_{{N},k} \end{aligned}$$

(18)

$$\begin{aligned}&\frac{1}{l}\left[ \begin{array}{cc} 1 &{}\quad 1 \\ 1 &{}\quad 1 \\ -1 &{}\quad -1 \\ -1 &{}\quad -1 \end{array}\right] \left[ \begin{array}{c} m_{\mathrm{A},k} \\ m_{\mathrm{B},k} \end{array}\right] + \frac{\rho gl}{2} \cos \theta \left[ \begin{array}{c} 1 \\ -1 \\ 1 \\ -1 \end{array}\right]\le \left[ \begin{array}{c} 1\\ 1 \\ 1 \\ 1 \end{array}\right] q_{{V},k} \end{aligned}$$

(19)

Noting that both of these forces are carried over the area $a_{{N},k}$, they can be transformed into stresses. To combine the shear and normal stresses the Von Mises’ yield criterion can be employed, which can be rearranged to give the following conic constraint:

$$\begin{aligned} (q_{{N},k}) ^2 + 3 (q_{{V},k}) ^2 \le \sigma ^2 (a_{{N},k}) ^2 \end{aligned}$$

(20)

Alternatively, to maintain a linear formulation, this can be approximated using linear constraints. The simplest conservative way to do this is to use a plane which intersects the cone of Eq. (20) when $q_{{N},k} = 0$ and when $q_{{V},k}= 0$; this (along with the non-negativity of $q_{{N},k}$ and $q_{{V},k}$, implied by Eqs. (21) and (22) respectively) defines a subset of the cone of Eq. (20). The required linear constraint is therefore:

$$\begin{aligned} q_{{N},k} + \sqrt{3} q_{{V},k} \le \sigma a_{{N},k} \end{aligned}$$

(21)

Note that the use of the Von Mises yield constraint restricts elements to have equal stress limits in tension and compression.

2.5 Beam formulation 2: pinned joints

The beam formulation in the previous section provides a conservative method of modelling frames when both self weight and multiple load-cases must be considered. However, the optimization problem produced using this formulation contains many more variables and constraints than an equivalent problem using the catenary or lumped mass formulations (see Appendix A for details).

In this section, a further formulation will be derived; this will use elements that are very similar to those described in the previous section, except that they will now be assumed to be pin-ended. It will be shown that this can produce a formulation of comparable computational complexity to the catenary and lumped mass formulations.

2.5.1 Equilibrium

Firstly, the end moments of all elements are fixed to be zero, and the corresponding optimization variables are therefore not required. The moment equilibrium constraints at each node are also removed. The equilibrium constraint, Eq. (12), then becomes:

$$\begin{aligned} \left[ \begin{array}{c} -\cos \theta \\ -\sin \theta \\ \cos \theta \\ \sin \theta \end{array}\right] \begin{bmatrix} q_k \end{bmatrix} + \frac{\rho g L}{2} \left[ \begin{array}{c} 0 \\ -1 \\ 0 \\ -1\end{array}\right] \begin{bmatrix} a \end{bmatrix} = \left[ \begin{array}{c} f^x_{{\text A},k} \\ f^y_{{\text A},k} \\ f^x_{{\text B},k} \\ f^y_{{\text B},k} \end{array}\right] \end{aligned}$$

(22)

Note that this is now identical to the equilibrium condition used in the lumped mass formulation. However, in this case the yield conditions outlined in the section below will give rise to a significantly larger value of a for any given value of q.

2.5.2 Yield

The yield constraints will now be derived, starting from the constraints developed in the previous section.

Moment yield As the end moments of the member are now zero, the maximum moment will equal $M_{\mathrm{sw}}$, as defined in Fig. 6 and Eq. (15). This will be the maximum value of both the exact and approximate distributions shown in Fig. 6, so it is immaterial which of these is assumed.

As the bending moment in the member now depends only on self-weight, it will not change between load-cases. In other words, the load-case specific variables $a_{{M},k}$ can be replaced with a single value $a_M$, which can be defined from Eqs. (16) and (17) to be:

$$\begin{aligned} \frac{\rho g |\bar{x}|l }{8} a = \frac{\sigma d}{2} a_M \qquad \therefore \frac{\rho g |\bar{x}|l}{4\sigma d} a=a_M \end{aligned}$$

(23)

Axial and shear yield The shear force in the member is caused by the self-weight alone once the end moments have been removed. Therefore the maximum absolute value of the shear force ($q_{{V},k}$) will be invariant between load-cases, and can be replaced with a single value $q_V$, which is defined as $|\frac{\rho g l a}{2} \cos \theta |$. Note also that this implies that the worst case points for shear and normal will always coincide in the pin jointed case, rather than this simply being assumed, as in the rigid jointed derivation.

The maximum axial force, $q_{{N},k}$ may still vary between load-cases, and is still defined by the expression $|\frac{\rho g l a}{2} \sin \theta |+ |q_k|$. Combining these expressions using the linearised Von Mises constraint, Eq. (21), gives:

$$\begin{aligned} |q_k|+ |\frac{\rho g l a}{2} \sin \theta |+ \sqrt{3}|\frac{\rho g l a}{2} \cos \theta |\le a_{{N},k} \end{aligned}$$

(24)

Equality may be assumed as this is the only constraint on $a_{{N},k}$, and thus the constraint can be simplified to give:

$$\begin{aligned} |q_k|+ \frac{\rho g }{2} |\bar{y} |a + \sqrt{3}\frac{\rho g }{2} |\bar{x} |a=\sigma a_{{N},k} \end{aligned}$$

(25)

where $\bar{y} = y_{\mathrm{B}} - y_{\mathrm{A}}$.

Combined yield constraint The moment and axial/shear yield constraints are combined using the constraint that $a_M + a_{{N},k} \le a$. From Eqs. (23) and (24) the following can be obtained:

$$\begin{aligned} \frac{\rho g |\bar{x}|l }{4 d} a +\frac{\rho g }{2} |\bar{y}|a +\sqrt{3}\frac{\rho g }{2} |\bar{x}|a +|q_k\vert \le \sigma a \end{aligned}$$

(26)

This may be rearranged to give a form which is comparable with the yield condition for the classical lumped mass formulation:

$$\begin{aligned} |q_k|\le \left( \sigma - \frac{\rho g }{2} |\bar{y}|-\sqrt{3}\frac{\rho g }{2} |\bar{x}|- \frac{\rho g |\bar{x} |l }{4 d}\right) a \end{aligned}$$

(27)

Comparing this with Eqs. (1c) and (1d), the additional terms concerning $|\bar{y}|$ and $|\bar{x}|$ in Eq. (27) can be interpreted to represent reductions in the effective limiting stress of the member, caused by the need to carry its own self-weight. If the values of $|\bar{y}|$ and $|\bar{x}|$ are sufficiently large, the term in the bracket will become zero or even negative, which implies that such elements are not feasible, and should therefore be excluded from the ground structure. This is discussed in more detail in Sect. 3.1.2.

3 Comparison of formulations

Next, the performance of the formulations described in Sect. 2 are compared. In Sect. 3.1 individual elements are considered, using examples with real-world values (Sect. 3.1.1), and also observing differences in predicted limiting span (Sect. 3.1.2). In Sect. 3.2, the different formulations are used to solve a simple textbook-style problem, with results compared in terms of optimal form, volume, and numerical convergence characteristics.

3.1 Comparison of individual elements

3.1.1 Single element problem

Consider the problem setup shown in Fig. 8, with material assumed to have a stress limit, $\sigma$, of 500 MPa and unit weight, $\rho g$, of 80 kN m$^{-3}$. The volumes of material required to support the applied load using the different formulations are shown in Fig. 9.

Fig. 8

Single element example: problem setup

Firstly, the classical lumped formulation requires an element with cross-sectional area $a = 0.012\ \text {m}^2$, equivalent to a solid circular cross-section of radius 62 mm. Note that this result does not depend on the value of the material unit weight, and indeed the same result would be obtained if self-weight was neglected entirely.

A catenary element for this example would have a maximum dip (or rise, if the force was reversed so as to be compressive) of 1.80 m. At midspan, where the element is horizontal, the cross-sectional area will be precisely equal to that of the lumped formulation, i.e. 0.012 m$^2$; this increases slightly to a maximum of 0.120034 m$^2$ at the end points. The total volume of the element is 3.600691 m$^3$, a mere 0.02% increase in overall volume compared to the lumped case; however the material is now optimally distributed over a much larger structural depth.

Considering the pinned beam formulation, from Eq. (23) it can be found that $0.012 \frac{l}{d}a = a_M$, showing that the proportion of the cross section used to carry the bending stresses induced by the self-weight is dependent on the bending depth d, or, more conventionally, on the beam span:depth ratio $\frac{l}{d}$. For example, a value of 20 for the beam span:depth ratio (as in Fig. 9) would result in 24% of the cross-section being used to carry bending.

From Eq. (27) the required overall area (in m$^2$) of the beam element can be found to be $a = \frac{6}{479.22 - 6\frac{l}{d}}$, which again will depend on the span:depth ratio. Even when the beam is very deep ($\frac{l}{d}\rightarrow 0$) the required area will be 0.01252 m², a 4.4% increase over that required by the lumped formulation; this increase accounts for the need to carry the shear forces imposed by the self-weight loading. For a span:depth ratio of 20 the required area a will be 0.0167 m². The use of the linear approximation to the Von Mises’ criterion can be calculated to cause an increase in volume of 4.2% when the beam is very deep, or 5.7% when $\frac{l}{d}=20$.

As shown in Fig. 9, the required material in the $a_N$ section (i.e. the ‘web’, carrying axial and shear forces) does not depend on the situation at the ends of the member, and is therefore the same for both pin-ended and rigid jointed beams. The assumption that maximum shear and normal stresses are co-incident is found to be true in both these cases, as the element is horizontal and thus has a constant normal force (similarly, this assumption is also true for all vertical elements, and the aforementioned case of elements with end moments of zero).

For the rigid-jointed beam formulation, the optimal moment distribution (using the approximated distribution in Fig. 6) occurs when the moment at the fixed support, $m_2$, is equal in magnitude to the moment at the quarter point. Therefore, the moment to be resisted will be $0.75M_{\mathrm{sw}}$. This results in an element with total area $a = 0.01583\ \text {m}^2$ if the span:dip ratio is 20, giving a total volume of 4.7486 m³.

Fig. 9

Single element example: total structural volumes using the different formulations, with the influence of the approximations described in Sect. 2 indicated

If the exact, parabolic, distribution of the bending moment is instead assumed, then the minimum moment to be resisted will be obtained when $m_2$ is equal to $0.684M_{\mathrm{sw}}$, leading to a total member area $a=0.01525\ \text {m}^2$ for a beam with span:dip of 20. This implies an error of 3.8% caused by the approximated moment distribution employed in this paper. Note that this example demonstrates a case that is particularly challenging for this approximation; the self-weight moment is large, and the end moments are highly asymmetrical. Of course, if a more precise approximation is required then the moment distribution may be discretized using a larger number of line segments.

The most significant assumption (in terms of impact on the volume) within the beam formulations is that the elements should be prismatic, i.e. that $a, a_{{M},k}$ and $a_{{N},k}$ are constant along the bar. This may be quantified by comparing the single element solution above with the result obtained when many rigid-jointed beam elements are used, arranged along the centre-line of the beam. For this case, the single element (i.e. prismatic) solution has a volume 16.7% greater than the result using 100,000 elements. Reasonable approximations are possible, however, with more modest resolutions; using 10 elements increases the volume by just 3.2%.

3.1.2 Element volumes and limiting spans

It was noted in Fairclough et al. (2018) that catenary elements have a maximum horizontal span of $\frac{\pi \sigma }{\rho g}$, although they have no limit in the vertical direction; this limit is unchanged by the multiple load-case extension described here. Conversely, both the weightless and lumped mass approaches may permit elements of unrestricted length—assuming appropriate boundary conditions. The electronic supplementary material (ESM) contains plots of the limiting spans for all the formulations considered here, alongside the relative volumes of shorter elements.

This indicates that the beam formulations are much more heavily influenced by self-weight. The maximum horizontal span for a beam element, even when the structural depth is large, is $\frac{2}{\sqrt{3}}\frac{\sigma }{\rho g}$, which is just 37% of the span possible using the same material in catenary form. The beam elements are also restricted in their vertical height. Even at much shorter spans, the use of beam elements implies greater impact from self-weight, with effects noticeable at a span roughly a fifth of the equivalent with catenary elements.

Note that in the layout optimization formulation, individual potential elements that lie outside their respective limits should be eliminated from the ground structure. For these ‘impossible elements’, the functions outlined in Sect. 2 may be undefined or complex-valued, or may give coefficient values that would lead to infeasible problems.

3.2 Comparison of resulting structures

In this section, each of the formulations developed in Sect. 2 is in turn used to solve the same problem, allowing differences in the resulting structures to be identified.

3.2.1 Problem description

The problem considered involves a uniformly distributed load of magnitude $\omega$ applied between a pair of pinned supports, as shown in Fig. 10. The material to be used has the same limiting stress, $\sigma$, in both tension and compression (limiting Von Mises stress in the beam-based formulations), with unit weight $\rho g$. Initially, only a single load-case is considered. To discretize the load, the Type-III loading defined by Darwich et al. (2010) is used.

Fig. 10

Single span example: problem definition

Similar problems have been considered analytically, albeit without consideration of self-weight (Hemp 1974) and also with different loading distributions (Chan 1975), variations in permitted limiting tensile and compressive stresses (Pichugin et al. 2012) or with variable height loading (Darwich et al. 2010; Tyas et al. 2011). A version involving multiple load-cases was considered by Sokół and Rozvany (2013), where each of nine equally spaced point loads was applied separately. In all of these cases, the design domain has generally been taken to be the half plane above the supports, though to keep the problem size manageable in the numerical studies the domain height has been limited to half the span, and the horizontal extent of the problem to between the two supports. Symmetry boundary conditions of the type used by Fairclough and Gilbert (2020) are employed so that only half of the domain needs to be explicitly modelled, when loading is symmetric; these behave identically to standard symmetry boundary conditions (i.e. roller/pin supports).

3.2.2 Influence of nodal discretization

In the first case considered the span, L, between supports is taken as $0.4\frac{\sigma }{\rho g}$; for a steel material with limiting stress 200 MPa and unit weight 80 kN/m$^3$, this equates to a span of 1 km. Figure 11 shows the normalized volumes for the solutions obtained using each formulation, at various nodal resolutions; Fig. 12 shows the resulting structures for the $n_x = 100$ case. Here $n_x$ is defined as the number of nodal divisions across the full span. The spacing of nodes is the same in the horizontal and vertical direction, and thus the modelled half-span contains a grid of $(0.5n_x + 1) \times (0.5n_x + 1)$ nodes. All pairs of nodes have the potential to be connected using the adaptive member adding method, and thus the largest $n_x = 160$ problems permit over 330 million potential members. For the beam formulations, the element depth, d, was chosen to be $\frac{L}{1000}$.

Fig. 11

Single span example: convergence of different self-weight models. Solid lines show fit line, dashed lines show values of $V_\infty$. Left: comparison of results for all models. Right: detail of region containing lumped and catenary model results

Table 1 Single span example: extrapolated volumes and span:dip ratios, $\frac{L}{H}$, for the solutions obtained

To extrapolate a volume for infinitely many divisions, the approach of Darwich et al. (2010) was employed. The extrapolated volumes, $V_\infty$, are given in Table 1 and shown as dashed lines in Fig. 11. The value of $V_\infty$ obtained here with the weightless formulation is just 0.01% away from the value obtained by Pichugin et al. (2012) (who used higher nodal resolutions in the y direction and also higher values of $n_x$).

The forms in Fig. 12a–c all resemble the numerical result of Pichugin et al. (2012, Fig. 2)—a modified version of Hemp’s arch (Hemp 1974) with a horizontal tie bar in the centre. However, the lumped and catenary approaches (Fig. 12b, c), substantially increase the heights of the structures (see $\frac{L}{H}$ values in Table 1).

With the beam formulations (Fig. 12d, e), the centre of the arch does not directly support any hangers. At this point the thickest elements form a straight load path, whilst surrounding thinner members form a framework to more efficiently carry the self-weight. The beam formulations also display significantly increased resolution-dependence, which is unsurprising since the bending induced by self-weight is proportional to element length squared.

Fig. 12

Single span example ($L= 0.4\frac{\sigma }{\rho g}$): resulting optimized layouts using each model of self-weight, a weightless; b lumped mass; c catenary; d rigid jointed beam; e pinned beam

Fig. 13

Single span example: effect of varying span on optimized volume

Fig. 14

Single span example ($L=1.6\frac{\sigma }{\rho g}$): resulting layouts using different models of self-weight, a lumped mass; b catenary

3.2.3 Influence of span

The effect of varying the span length L is now investigated. Figure 13 shows the corresponding volumes with $n_x =100$ over a range of spans up to $L=1.6\frac{\sigma }{\rho g}$ (around 4 km with 200 MPa steel). The volumes in Fig. 13 have been scaled to highlight the changes in volume caused by scale effects, such that the weightless solutions form a straight horizontal line. The time required to solve these problems is discussed in Appendix B; notably, the pinned beams require only around a quarter of the time to solve compared to the equivalent problem with rigid joints.

In general, the increase in span leads to a taller structure. For example Fig. 14b shows the resulting structure using the catenary formulation at $L=1.6\frac{\sigma }{\rho g}$ (c.f. Fig. 12c). A similar pattern was observed using the beam formulation, although the height of those structures became restricted by the permitted domain height. In the beam solutions, there is also a preference towards moving material towards the supports, extending the triangular regions evident in Fig. 12d–e. There is a suggestion that a similar effect may be occurring in the catenary solution (Fig. 14b), although due to the increased efficiency of the catenary approach (see Sect. 3.1.2) the effect is less pronounced.

The difference between modelling the problem by exploiting the symmetry plane and by modelling the whole domain was also tested. For the weightless formulation and the three new approaches proposed here, no significant difference in terms of the form or volume of the structure was observed, although problems utilizing the symmetry plane required only around one third of the CPU time to solve.

However, when using the lumped mass method, the results obtained when modelling the whole plane demonstrated a key weakness of the method—its propensity to generate unrealistic solutions involving very long elements. This is evident in the solution shown in Fig. 14a, which contains very long unsupported elements along the top of the structure. Using these elements allows the optimized form to transmit the force along the top of the structure without incurring any additional self-weight load in the critical mid-span regions. Figure 13 shows that the volumes of the catenary and lumped mass approaches are very similar until the point at which these unrealistic elements emerge. In other cases, the lumped mass formulation may over-estimate the volume of material required. In the present example this is particularly notable in the near-vertical hangers; these should vary in area along their length due to the changing load from self-weight, yet the lumped mass formulation can only model them with constant cross-section. This actually causes the lumped mass solution to have a slightly ($\le 0.3\%$) higher volume than the catenary solution at shorter spans.

4 Combined approaches

The self-weight modelling approaches described in Sect. 2 are compatible with each other, making it possible to construct problems that simultaneously involve multiple approaches. The corresponding general formulation is given in Appendix A. This section considers the case where each pair of nodes is connected by multiple potential members of different types.

The major motivation behind adopting a combined approach stems from the behaviour of the catenary elements as their axial force is altered. The catenary approach described in Sect. 2.3 relies on assumptions that may not be conservative when multiple load-cases are present. Namely, the ‘lumping’ of the unused portions of the cross section to the end points. The practical result of this is to ignore the bending stresses that would be generated by this material. The implications of this assumption vary in severity depending on the application involved. In this section, this will be explored with reference to a number of variations on the single element problem shown in Fig. 8.

As the problematic catenary elements are by definition not fully stressed, they will be analysed as an elastic material. Initially, the problem is set up exactly as shown in Fig. 8, and the resulting catenary element is approximated using 100 straight beam elements in the GSA structural analysis package (Oasys 2021) using a solid circular cross section of the required area. The horizontal force, marked as f in Fig. 8, is then reduced and the structure is again analysed. The structure itself, and therefore the loading from gravity, remains unchanged throughout.

Initially a linear-elastic model is used to analyse the structure; this results in very large bending stresses, even for very small variations in the applied load. For the realistic values considered in Fig. 8, reducing the applied force to just 90% of the design value increases the stress to 6270 MPa, more than 12 times the prescribed design strength of in this case 500 MPa. This value is particularly large due to the slenderness of the element, which does not provide a large structural depth (recall that the radius of the element is approximately 62 mm) to generate the required bending resistance.

To further investigate this, the same problem has been investigated with values of the horizontal force f multiplied by 100 and 10,000, leading to catenaries with radii of approximately 620 mm and 6200 mm, respectively. These thicker catenaries do reduce the problem, yet they still require stresses above the design level; at 90% loading these problems have peak stress of 1030 MPa and 508 MPa, respectively.

Fig. 15

Single element example: elastic analysis results for catenary elements when the applied load f is reduced below the design load r

However, this issue can be better understood with the help of a large deformation analysis. The GSrelax solver in GSA (Oasys 2021) is here used for this purpose, with the problem otherwise set up as previously described. The resulting peak stresses in each case are shown in Fig. 15. It can be seen that for all the magnitudes of design load, the stress in the element reduces as the axial force is initially reduced from its design value.

For the original case, which was chosen to be representative of the values for a stay in a cable stayed bridge, the stress very closely matches the values expected for a weightless member until very low values of utilization are involved. Even once they diverge, the catenary still has stresses well below the design stress limit. The larger catenaries do show larger than prescribed stresses when the applied load is very low, principally caused by bending action.

The case $r=6e^5$ implies a catenary with radius approximately 620 mm, similar to the radius of the main cables proposed for the Strait of Messina suspension bridge, which have a radius of 637 mm (Walker et al. 2011). Structural members of this size and larger would very rarely be realized as a solid cross-section. For example, the proposed Messina cables are constructed from 354 smaller strands resulting in 19% void within the circular section. Assuming the whole section still acts compositely, this would lead to an increased bending resistance for the given cross-sectional area, relative to that assumed here.

However, if this analysis is repeated but now with a compressive force, a very different picture emerges. The stress values obtained using the linear elastic model are unchanged, but the large deformation analysis does not successfully converge. Physically, this is the result of the shallow arches involved being very susceptible to snap-through effects, leading to a large change in the shape of the element, eliminating its resistance.

This study serves to show that the catenary elements are most suitable for modelling cable type elements with small cross sections and tensile forces. Thus in the examples presented in Sect. 5 catenary elements are generally permitted to carry tensile forces only. Beam elements are instead used to carry the compressive forces. This is simply achieved by removing the variables corresponding to the compressive catenary form from the problem. Thus the ground structures used resemble that shown in Fig. 16. Note that the beam elements are still permitted to carry tensile forces, but as the catenary elements are more efficient they will usually be preferred.

Fig. 16

Example ground structure with tensile catenary (blue) and straight beam elements (red) present (c.f. Fig. 1c)

To make use of the adaptive ‘member adding’ solution method in this combined approach, the initial ground structure consists of adjacent connectivity members in both the beam and catenary models. During the member adding phase, each material model is checked separately, and members of the appropriate type are added where required.

5 Examples

This section presents results for a number of simplified real-world problems. Firstly in Sect. 5.1, the single-span example originally considered in Sect. 3.2 is revisited, now using the combined approach described in Sect. 4 and also considering multiple load-cases. Various bridge type design problems comprising multiple spans are then considered in Sects. 5.2 and 5.3. Finally, in Sect. 5.4, the simple modifications required to use the formulations from Sects. 2.3 and 2.5 in three dimensions are described, then demonstrated via application to a stadium roof-like example problem.

5.1 Single span example revisited

The scenario from Sect. 3.2 is considered for spans $L=0.4\frac{\sigma }{\rho g}$ and $L=1.6\frac{\sigma }{\rho g}$, using both pinned beam and rigid jointed beam models—combined with catenary elements in both cases. The limiting tensile stress of the catenary elements and the maximum von Mises stress for the beam elements both have the same value $\sigma$, though the catenary elements are not permitted to carry compressive forces.

In addition to the single load-case problem described above, a multiple load-case problem is also considered. Specifically, an additional load-case in which only one half of the domain is loaded (to the same magnitude, $\omega$, as the uniform case) is considered; the mirror image of this load-case is considered implicitly.

Fig. 17

Single span example: volumes of optimized structures when both tensile catenaries and beam elements are allowed throughout the domain, with relative contributions from the beam members and catenary elements shown. Volumes obtained when using only a single element type are also indicated for comparative purposes

Fig. 18

Single span example ($L=0.4\frac{\sigma }{\rho g}$): results obtained when both catenary and beam elements are permitted throughout the domain for the scenarios indicated. Red/brown lines indicate beam elements and blue lines indicate catenary elements

The volumes for each case are shown in Fig. 17, which also shows what proportion of the resulting structure is composed of beam elements and catenary elements. It can be seen that the multiple load-case solutions employ a larger proportion of the more versatile beam elements than the corresponding single load-case solutions. For longer spans, a greater proportion of the volume is consumed by beam elements; this is likely due to the high sensitivity to self-weight of the beam formulation (as discussed in Sect. 3.1.2).

In general, the increase in volume between the single and multiple load-case problems is relatively small; however the optimal forms differ noticeably, as shown in Fig. 18. The overall form of all of the single load-case solutions is similar to the results shown in Fig. 12, comprising a thick arch region with hangers spaced to avoid a triangular region around midspan.

Fig. 19

Three span problem ($L = 0.8\frac{\sigma _T}{\rho g}$): a problem definition, highlighting load-cases; b boundary conditions chosen to match the infinite bridge case (horizontal only supports at anchorage, vertical only at pylon)—load-case 1 only; c fixed pin supports at both pylon and anchorage—load-case 1 only; d as c but all load-cases considered

Fig. 20

Three span example: results using the catenary formulation, compared with selected combined beam and catenary solutions and infinite span bridge solutions from Fairclough et al. (2018)

The multiple load-case results in Fig. 18 show a more complex form, although an outer arch of beam elements is still evident. Secondary structure results in a steeper arch at the supports than for the corresponding single load-case problems. Beam elements are also used below the arch region when multiple load-cases are present, triangulating much of the structure. This is reminiscent of the multi-layered laminates that have been observed in multiple load-case problems without self-weight (Sokół and Rozvany 2013).

5.2 Three span example

A three span bridge problem is shown in Fig. 19. If the supports at the outer anchorages are assumed to provide restraint only in the horizontal direction, and the pylon supports provide restraint only in the vertical direction, then this problem becomes essentially identical to a section of a bridge with an infinite number of spans, as considered e.g. by Pichugin et al. (2015), Beghini and Baker (2015), Fairclough et al. (2018). In particular, Fairclough et al. (2018, Fig. 9) obtained solutions for this problem using catenary elements, though only for single-load case problems. In addition to the optimized form and a simplified version thereof, results for size and geometry optimized suspension and cable-stayed layouts were also given.

Here, a three span version of this problem is considered. To aid comparison, initially the catenary formulation is used in isolation; Fig. 20 shows the designs generated. The domain has been discretised using 60 nodes horizontally across the whole domain, matching the resolution used by Fairclough et al. (2018), and the material properties were also chosen to provide results for the case when $\sigma _T =3\sigma _C$, as considered previously. This case better represents the real-world situation, where the limiting stress in tensile cable members (made of drawn steel wire) is usually much higher than for compressive members (made of hot rolled steel).

The result for a case involving a single load case and boundary conditions corresponding to the infinite span bridge is first used to establish a benchmark value, $V_0$. The support at the anchorage is now altered to also provide vertical restraint; this reduces the optimal volume to $0.997 V_0$, i.e. just a 0.3% reduction. If horizontal support is also added at the base of the pylon, the volume reduces to $0.993V_0$. From this it is evident that, when a single uniform load-case is present, the difference in support conditions between an infinite bridge and this three span bridge is very small.

These small reductions in volume are generated through variations in the forms of the optimized structures, where the cables in the side span are at a slightly shallower angle than the main span; see Fig. 19b and c. Such an alteration would not be possible with the more restricted cable-stayed and suspension forms presented in Fairclough et al. (2018, Fig. 9), so these results would not be altered by the change in boundary conditions. Figure 20 shows computed optimal volumes for rationalized structures from Fairclough et al. (2018) alongside results for the three span case modelled using catenary elements.

Figure 20 also shows the optimal volumes obtained for the same problem when multiple load-cases are involved; the cases are as shown in Fig. 19. Such pattern load cases could not be supported by the typical forms of suspension and cable stayed forms without requiring either bending resistance at the joints, or consideration of large-deformation effects.

From Fig. 20, it can be seen that the volume of material required to construct the optimal structure for the multiple load-case problem is still lower than the volume of material required to construct a suspension or cable stayed form when just a single uniform load-case is involved. As the single load-case problem provides a lower bound on the possible volume when multiple load-cases are involved, it can be concluded that cable stayed and suspension bridge forms use respectively at least 13% and 34% more material than is necessary.

Fig. 21

Two span example (pinned beam and catenary elements): a problem definition; b solution for $L=\frac{0.1}{15}\frac{\sigma _T}{\rho g} \approx 50$ m; c solution for $L= \frac{4}{15} \frac{\sigma _T}{\rho g} \approx 2$ km; d solution for $L=\frac{8}{15}\frac{\sigma _T}{\rho g} \approx 4$ km

Fig. 22

Two span example: optimized volumes, with the (geometry optimized) solutions shown in Fig. 21 indicated by crosses

Fig. 23

Concept bridge for crossing requiring multiple very long spans, based on the results described in Sect. 5.3

This problem has also been solved using the combined catenary and pinned beam approach described in Sect. 4. Stresses in the beam elements are limited to $\sigma _C$ whilst the catenary elements can now carry only tensile stresses, up to $\sigma _T$ where $\sigma _T=3\sigma _C$. The beam element depth is set to $\frac{L}{1000}$.

As in the example presented in Sect. 3.2.2, the beam element models are very sensitive to the chosen nodal resolution. Halving the nodal spacing (from 60 to 120 nodes across the domain), reduces the volume by 17%, whilst the same change in the catenary only models causes a reduction of just 2%. The volumes of the solutions with 120 nodes across the domain are included in Fig. 20.

The form of the optimal structure to carry the multiple load-case problem uses arch type forms close to the anchorage, which may be impractical from a constructibility perspective. However, as there is only a single pin support available, there is only a limited range of possible forms in that area. To address this, the next example will make use of a back-span, i.e. a line along which support is available at any point.

5.3 Two span example

The example shown in Fig. 21a shows a problem consisting of a bridge with two spans of equal length L. In addition to a central pylon support, pinned supports may be located anywhere within a backspan of length $\frac{L}{2}$ beyond each end of the deck. The first load-case is a uniformly distributed load of magnitude $\omega$ across both spans, whilst the multiple load-case problem also has a case where the load (still of magnitude $\omega$) is applied to only one span (the mirror case is applied implicitly). The layout optimization problem is solved using a Cartesian grid comprising 102 divisions along the base of the domain.

The problem is solved using the combined catenary and beam formulations, with the performance of both pinned and rigid beam approaches evaluated. The limiting tensile stress of the catenary elements, $\sigma _T$, has again been set to three times the limiting stress of the beam elements, to approximately reflect real-world conditions, and the beam element depth is set to $\frac{L}{1000}$. Figure 22 shows the optimal volumes for each approach for a range of spans and for both the rigid and pinned joint formulations. It can be seen that the rigid and pinned joint models show close agreement in terms of optimal volume, with the pinned beam result lying within 3% of the rigid jointed beam result. As the pinned beam formulation required approximately half the computational time to solve, this is likely to be appealing in practice.

Figure 21 shows the structures obtained when using the pinned beam model. These have been rationalized using the geometry optimization procedure of He and Gilbert (2015), which increased clarity somewhat and had a small ($\le 0.7\%$) effect on the volumes, as shown in Fig. 22. The results obtained using the rigid jointed approach were qualitatively similar to the pin jointed results, although the transition between different forms occurred at slightly higher spans.

At the shortest spans, the unequal loading is supported by a double arch form comprising primarily of beam elements, with the presence of upper and lower arches giving additional bending strength (Fig. 21b). As the spans lengthen, the arch form becomes inefficient, as is evident from Fig. 22, which shows an initially relatively steep increase in volume with span when multiple load-cases are involved. This is likely because a large proportion of the material forming the structure is initially located around midspan, and this must be carried an increasingly long distance to the supports.

The arch form is then replaced by the form shown in Fig. 21c; this structure is similar to the single load-case solution to the infinite span problem, consisting of regions of compressive members radiating out from the supports, and tensile members connecting these to the loaded deck. To deal with the multiple load cases, additional tie cables connect the tops of each of the pylon regions. As the span increases further (Fig. 21d), it becomes preferable to connect directly to the base of the outer pylons.

Based on the results shown in Fig. 21, a simplified design for a multiple span bridge has been proposed, as shown in Fig. 23. This is similar to the simplified split-pylon designs proposed by Fairclough et al. (2018), though now with the addition of a tie cable between the tops of adjacent pylons to carry the bending induced when adjacent spans are loaded unequally. Geometry optimization has been used to refine the nodal positions of the simplified form, and the problem has been extended to the third dimension by assuming two parallel structures with bracing between the pylon elements, following typical real-world practice for suspension and cable-stayed bridges.

Figure 21 shows only a portion from the centre of the bridge; as demonstrated in this section and in Sect. 5.2, the boundary conditions at the anchorages can significantly influence the optimal form, making it difficult to propose a general form for these regions.

5.4 Three-dimensional example

The catenary and pinned beam examples can be extended to three dimensions by simply performing all element calculations in a local element-specific co-ordinate system in the plane containing the vector along the element and the gravity vector. The coefficients for the equilibrium constraints should then be projected back to the global co-ordinate system.¹ It will be necessary to have three force equilibrium constraints per node, rather than the two required for planar problems.

Fig. 24

Three-dimensional stadium roof example: plan view of problem, with darker grey shaded region denoting the independent (modelled) design domain

Note that the rigid jointed beam problem presents a greater challenge in its extension to three-dimensional problems; torsional loading must be considered, as must minor axes of bending; furthermore the orientation of the element about its axis must be decided upon. Further consideration of these elements is therefore beyond the scope of this paper.

Fig. 25

Three-dimensional stadium roof example: optimized volumes for domains of different radius, with the (geometry optimized) solutions shown in Fig. 26 denoted by crosses

Fig. 26

Three-dimensional stadium roof example: optimal forms for a $R = 0.001\frac{\sigma _T}{\rho g}$; b $R=0.08 \frac{\sigma _T}{\rho g}$; c $R = 0.16 \frac{\sigma _T}{\rho g}$

A three-dimensional problem involving an annular design domain, such as may be present for the design of a stadium roof, will now be considered. The specification is shown on plan in Fig. 24, and the domain extends vertically 0.3R. The independent domain region is discretized using a grid of 140 nodes, placed at grid points located at $0.1R$ spacings on the symmetry planes, and at the mid- and quarter-points of a line connecting corresponding points. The limiting stress in the catenaries $\sigma _T$ is taken as twice the permitted von Mises stress of the beams, and the depth of the beam elements is set as $0.02R$.

It is of interest to study the influence of the span (varied by changing the radius R) on the optimal designs generated and the corresponding structural volume. The optimized volumes are shown in Fig. 25 and the corresponding forms are shown in Fig. 26. It is evident that the form obtained changes markedly as the span is increased. At the shortest spans, the solution includes a compression ring towards the centre of the design domain, with half-arches carrying load back to the supports. As the span increases, the compression ring moves towards the outside of the domain. This increases the length of the ring, and hence its volume, but reduces the distance that the weight of the ring must be transmitted to the supports. At the longest spans, the compression ring lies at the outer edge of the domain, with a cable net structure of catenary elements supporting the loads.

6 Concluding remarks

Layout optimization provides a powerful means of identifying materially efficient structural forms. To model problems involving self-weight and multiple load-cases using materials capable of deforming plastically, three new formulations have been presented herein; two formulations make use of beam elements and a third uses catenary elements, extending a previously proposed formulation to enable multiple load-cases to be handled. These formulations improve the accuracy of the solutions by removing the significant non-conservative errors introduced when using the traditional lumped mass modelling approach.

The primary drawback of the catenary formulation is the potential for second-order issues to arise, particularly when elements are loaded in compression. Conversely, the behaviour of long flexible tensile members, such as cables, has been shown to be adequately modelled using this approach.

The beam formulations provide greater versatility, although, due to the use of some conservative approximations, they also require the use of higher resolutions to obtain acceptable results. A combined approach has therefore been proposed that involves the use of catenary elements to model tensile members and beam elements to model compressive members. The efficacy of this approach has been demonstrated via application to a number of test problems. It is shown that the optimal form for a given problem can vary dramatically as the scale of the problem is varied, due to the differing influence of self-weight effects.

For the cases considered, the rigid and pinned beam formulations were found to give similar results, with the rigid jointed formulation providing only slight reductions in structural volume. Thus, due to the lower computational requirements associated with the pinned beam formulation, this is likely to be preferable in many situations.

In conclusion, a combined approach has been shown to be effective at identifying materially efficient structural forms for long-span structural design problems, when self-weight effects are significant. For bridge type problems, split-pylon forms were found to be efficient, with multiple load-cases carried through the use of additional tie cables. Although direct comparisons can be challenging, the indications are that significant material savings can be achieved compared to traditional cable-stayed and suspension bridge forms incorporating vertical pylons.

Appendices

Appendix 1: full combined formulation

The list of optimization variables associated with the formulations described in the paper are outlined in Table 2. The full formulation for a problem that takes advantage of all three self-weight modelling approaches described is shown in Table 3, though generally not all of these would be used simultaneously.

Table 2 Optimization variables for a problem containing c catenary elements, d pinned beam elements and e rigid-jointed beam elements

Table 3 Full formulation for problem containing all three element types

Appendix 2: implementation

Table 4 shows the total (wall clock) times required to solve the single span problem considered in Sect. 3.2.3 and the single load-case problems considered in Sect. 5.1. These times were obtained using a laptop with an Intel i7-6700HQ CPU and the linear programming problems were solved using MOSEK 9.1 (ApS 2020).

Note that quoted run times are given as ranges, obtained by solving each problem for a number of different spans. This is because the time required to obtain the solution to any given problem is somewhat variable, and hence presenting a range is more representative. Also, when implementing the formulations memory usage has been prioritized over computational time. For this reason details of potential elements were not stored between iterations when using the adaptive member adding procedure. However, this has a disproportionate effect on the catenary approach, as the calculations required to obtain the coefficients are more complex in this case. Furthermore, the adaptive member adding solution process was performed in a single thread, whereas benefits could be gained using multiple cores. As an example, the checks required at each iteration in the member adding procedure could be performed in parallel, which would likely significantly speed up the solution process when catenaries are involved.

Table 4 Single span problem: Times taken to solve $n_x=100$ single load-case problems for various spans using different formulations and combinations thereof