Variable-fidelity expected improvement method for efficient global optimization of expensive functions

Abstract

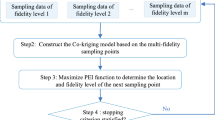
The efficient global optimization method (EGO) based on kriging surrogate model and expected improvement (EI) has received much attention for optimization of high-fidelity, expensive functions. However, when the standard EI method is directly applied to a variable-fidelity optimization (VFO) introducing assistance from cheap, low-fidelity functions via hierarchical kriging (HK) or cokriging, only high-fidelity samples can be chosen to update the variable-fidelity surrogate model. The theory of infilling low-fidelity samples towards the improvement of high-fidelity function is still a blank area. This article proposes a variable-fidelity EI (VF-EI) method that can adaptively select new samples of both low and high fidelity. Based on the theory of HK model, the EI of the high-fidelity function associated with adding low- and high-fidelity sample points are analytically derived, and the resulting VF-EI is a function of both the design variables x and the fidelity level l. Through maximizing the VF-EI, both the sample location and fidelity level of next numerical evaluation are determined, which in turn drives the optimization converging to the global optimum of high-fidelity function. The proposed VF-EI is verified by six analytical test cases and demonstrated by two engineering problems, including aerodynamic shape optimizations of RAE 2822 airfoil and ONERA M6 wing. The results show that it can remarkably improve the optimization efficiency and compares favorably to the existing methods.

Appendix

1.1 A.1 Hierarchical kriging

For an m dimensional problem, suppose we are concerned with the prediction of an expensive-to-evaluate (and unknown) hi-fi function y(x) : ℜ^m → ℜ, with the assistance of a cheaper-to-evaluate low-fidelity function y(x) : ℜ^m → ℜ. Assuming that the low- and hi-fi functions are observed at n_lf and n sites, respectively, the sample datasets for a HK model are

$$ {\displaystyle \begin{array}{l}{\mathbf{S}}_{\mathrm{lf}}={\left[{\mathbf{x}}_{\mathrm{lf}}^{(1)},\dots, {\mathbf{x}}_{\mathrm{lf}}^{\left({n}_{\mathrm{lf}}\right)}\right]}^{\mathrm{T}}\in {\Re}^{n_{\mathrm{lf}}\times m},{\mathbf{y}}_{\mathrm{S},\mathrm{lf}}={\left[{y}_{\mathrm{lf}}^{(1)},\dots, {y}_{\mathrm{lf}}^{\left({n}_{\mathrm{lf}}\right)}\right]}^{\mathrm{T}}\in {\Re}^{n_{\mathrm{lf}}},\\ {}\mathbf{S}={\left[{\mathbf{x}}^{(1)},\dots, {\mathbf{x}}^{(n)}\right]}^{\mathrm{T}}\in {\Re}^{n\times m},{\mathbf{y}}_{\mathrm{S}}={\left[{y}^{(1)},\dots, {y}^{(n)}\right]}^{\mathrm{T}}\in {\Re}^n,\end{array}} $$

(22)

where the subscript “lf” denotes “low fidelity.”

1.1.1 Kriging model of cheap low-fi function

To build a surrogate model for the hi-fi and expensive function, we first build a surrogate model for the lower fidelity but cheaper function that will be used thereafter to assist the prediction. Assume a random process corresponding to the unknown low-fi function y_lf(x)

$$ {Y}_{\mathrm{lf}}\left(\mathbf{x}\right)={\beta}_{0,\mathrm{lf}}+{Z}_{\mathrm{lf}}\left(\mathbf{x}\right), $$

(23)

where β_{0, lf} is an unknown constant and Z_lf(x) is a stationary random process. Then, we can follow (Sacks et al. 1989) to build a kriging based on the sampled data set  (S_lf, y_{S, lf}). After the kriging is fitted, the prediction of the low-fidelity function at any untried point x can be written as

$$ {\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)={\beta}_{0,\mathrm{lf}}+{\mathbf{r}}_{\mathrm{lf}}^{\mathrm{T}}\left(\mathbf{x}\right){\mathbf{R}}_{\mathrm{lf}}^{-1}\left({\mathbf{y}}_{\mathrm{S},\mathrm{lf}}-{\beta}_{0,\mathrm{lf}}\mathbf{1}\right), $$

(24)

where ${\beta}_{0,\mathrm{lf}}={\left({\mathbf{1}}^{\mathrm{T}}{\mathbf{R}}_{\mathrm{lf}}^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^{\mathrm{T}}{\mathbf{R}}_{\mathrm{lf}}^{-1}{\mathbf{y}}_{\mathrm{S},\mathrm{lf}}$; ${\mathbf{R}}_{\mathrm{lf}}\in {\Re}^{n_{\mathrm{lf}}\times {n}_{\mathrm{lf}}}$ is the correlation matrix representing the correlation between the observed low-fi sample points; $\mathbf{1}\in {\Re}^{n_{\mathrm{lf}}}$ is a column vector filled with ones; and ${\mathbf{r}}_{\mathrm{lf}}\in {\Re}^{n_{\mathrm{lf}}}$ is the correlation vector representing the correlation between the untried point and the observed low-fi sample points. The MSE of the kriging prediction at any untried x, the uncertainty due to the lack of a low-fi sample, is

$$ \mathrm{MSE}\left[{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)\right]={s}_{\mathrm{lf}}^2\left(\mathbf{x}\right)={\sigma}_{\mathrm{lf}}^2\left[1.0-{\mathbf{r}}_{\mathrm{lf}}^{\mathrm{T}}{\mathbf{R}}_{\mathrm{lf}}^{-1}{\mathbf{r}}_{\mathrm{lf}}+{\left({\mathbf{r}}_{\mathrm{lf}}^{\mathrm{T}}{\mathbf{R}}_{\mathrm{lf}}^{-1}\mathbf{1}-1\right)}^2/{\mathbf{1}}^{\mathrm{T}}{\mathbf{R}}_{\mathrm{lf}}^{-1}\mathbf{1}\right]. $$

(25)

The reader is referred to (Simpson et al. 2001; Martin and Simpson 2005; Toal et al. 2008) for more details of building such a kriging.

1.1.2 Hierarchical kriging for expensive high-fidelity function

By directly taking the low-fi kriging multiplied by a scaling factor β₀ as the model trend, the random process for the unknown hi-fi function is assumed as

$$ Y\left(\mathbf{x}\right)={\beta}_0{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)+Z\left(\mathbf{x}\right), $$

(26)

where β₀ is a scaling factor representing how the low-fi kriging matches the hi-fi function; ${\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)$denotes the prediction of low-fi kriging at x; and Z(x) is a stationary random process with zero mean. In this way, the trend of low-fi function is mapped to the sampled hi-fi data, resulting in a more accurate surrogate model for hi-fi function of interest. Then, a HK model (Han and Görtz 2012) can be built through the hi-fi sample datasets  (S, y_S). By minimizing the MSE of the prediction, the HK prediction for the hi-fi and expensive function at any untried x can be written as

$$ \widehat{y}\left(\mathbf{x}\right)={\beta}_0{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)+{\mathbf{r}}^{\mathrm{T}}\left(\mathbf{x}\right){\mathbf{R}}^{-1}\left({\mathbf{y}}_{\mathrm{S}}-{\beta}_0\mathbf{F}\right), $$

(27)

where F ∈ ℜⁿ is a column vector filled with predictions of the low-fi kriging at the sites of hi-fi samples; R ∈ ℜ^n × n is the correlation matrix representing the correlation between the observed hi-fi sample points; and r ∈ ℜⁿ is the correlation vector representing the correlation between the untried point and the observed hi-fi sample points

$$ {\displaystyle \begin{array}{l}{\beta}_0={\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}{\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{y}}_{\mathrm{S}}\\ {}\mathbf{F}={\left[{\widehat{y}}_{\mathrm{lf}}\left({\mathbf{x}}^{(1)}\right),\cdots, {\widehat{y}}_{\mathrm{lf}}\left({\mathbf{x}}^{(n)}\right)\right]}^{\mathrm{T}}\in {\Re}^n,\\ {}\mathbf{R}=\left[\begin{array}{ccc}R\left({\mathbf{x}}^{(1)},{\mathbf{x}}^{(1)}\right)& \cdots & R\left({\mathbf{x}}^{(1)},{\mathbf{x}}^{(n)}\right)\\ {}\vdots & \ddots & \vdots \\ {}R\left({\mathbf{x}}^{(n)},{\mathbf{x}}^{(1)}\right)& \cdots & R\left({\mathbf{x}}^{(n)},{\mathbf{x}}^{(n)}\right)\end{array}\right]\in {\Re}^{n\times n},\\ {}\mathbf{r}={\left[R\left(\mathbf{x},{\mathbf{x}}^{(1)}\right),\dots, R\Big(\mathbf{x},{\mathbf{x}}^{(n)}\Big)\right]}^{\mathrm{T}}\in {\Re}^n,\end{array}} $$

(28)

where R(x, x^′) is the spatial correlation function which only depends on the Euclidean distance between the two sites x, x^′. Generally, the R(x, x^′) can be a Gaussian exponential function or a cubic spline function, see (Han and Görtz 2012).

The MSE of the HK prediction at any untried x, the uncertainty due to lack of a hi-fi sample, is

$$ \mathrm{MSE}\left\{\widehat{y}\left(\mathbf{x}\right)\right\}={s}^2\left(\mathbf{x}\right)={\sigma}^2\left\{1.0-{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{r}+{\left[{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}-{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)\right]}^2/{\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\right\}. $$

(29)

In comparison to a cokriging model, the HK model does not need to calculate the cross covariance between low- and hi-fi samples. As a result, the correlation matrix of a HK model is relatively smaller. In addition, the HK model can provide a more reasonable MSE estimation than any of the existing kriging and cokriging models (Han and Görtz 2012), which is very beneficial for infill-sampling based on the method such as EI.

1.2 A.2 Standard expected improvement method

For using the expected improvement (EI) method proposed by Jones et al. (1998), we can assume that the prediction of the HK model at any untried site x obeys a normal distribution $\widehat{Y}\left(\mathbf{x}\right)\sim N\left[\widehat{y}\left(\mathbf{x}\right),{s}^2\left(\mathbf{x}\right)\right]$, with the mean being the surrogate prediction $\widehat{y}\left(\mathbf{x}\right)$ and the standard deviation s(x) being its root mean-squared error (RMSE). Then the statistical improvement at any untried location w.r.t. the best hi-fi objective function observed so far y_min is defined as:

$$ I\left(\mathbf{x}\right)=\max \left({y}_{\mathrm{min}}-\widehat{Y}\left(\mathbf{x}\right),0\right). $$

(30)

Then, the EI function can be written as

$$ EI\left(\mathbf{x}\right)=\left\{\begin{array}{cc}\left({y}_{\mathrm{min}}-\widehat{y}\left(\mathbf{x}\right)\right)\Phi \left(\frac{y_{\mathrm{min}}-\widehat{y}\left(\mathbf{x}\right)}{s\left(\mathbf{x}\right)}\right)+s\left(\mathbf{x}\right)\phi \left(\frac{y_{\mathrm{min}}-\widehat{y}\left(\mathbf{x}\right)}{s\left(\mathbf{x}\right)}\right),& if\kern0.8000001em s\left(\mathbf{x}\right)>0\\ {}0,& if\kern0.8000001em s\left(\mathbf{x}\right)=0\end{array}\right., $$

(31)

where Φ and ϕ are the cumulative distribution function and probability density function of standard normal distribution, respectively.

For a constrained optimization, the HK model for the constraint function, $\widehat{g}\left(\mathbf{x}\right)$, is also built. We can also assume the prediction at any untried site obeys a normal distributed, $\widehat{G}\left(\mathbf{x}\right)\sim N\left[\widehat{g}\left(\mathbf{x}\right),{s}_g^2\left(\mathbf{x}\right)\right]$, with the mean value being the predictor $\widehat{g}\left(\mathbf{x}\right)$ and the standard deviation being its RMSE s_g(x). Therefore, the probability of satisfying the constraint is

$$ P\left[\widehat{G}\left(\mathbf{x}\right)\le 0\right]=\Phi \left(\frac{-\widehat{g}\left(\mathbf{x}\right)}{s_g\left(\mathbf{x}\right)}\right). $$

(32)

And the constrained EI function can be given by

$$ CEI\left(\mathbf{x}\right)=E\left[I\left(\mathbf{x}\right)\cap \left[G\left(\mathbf{x}\right)\le 0\right]\right]= EI\left(\mathbf{x}\right)\cdot P\left[G\left(\mathbf{x}\right)\le 0\right]. $$

(33)

If there are N_C constraints, we should built N_C HK models for every constraint function, and the resulting constrained EI function is

$$ CEI\left(\mathbf{x}\right)= EI\left(\mathbf{x}\right)\cdot {\prod}_{i=1}^{N_{\mathrm{C}}}P\left[{G}_i\left(\mathbf{x}\right)\le 0\right]. $$

(34)

Then the following unconstrained sub-optimization problem is formulated as

$$ \mathbf{x}=\underset{{\mathbf{x}}_{low}\le \mathbf{x}\le {\mathbf{x}}_{up}}{\arg \max } CEI\left(\mathbf{x}\right). $$

(35)

A hybrid method of combing GA, Hooke and Jeeves pattern search, and BFGS gradient-based method is used to solve the above sub-optimization problem to suggest the new sample point (Han 2016a, b), which is to be evaluate by hi-fi numerical analysis again. Please note only the hi-fi sample point is obtained here, since the above EI function is defined based on the uncertainty due to lack of a hi-fi sample. Therefore, if we need to adaptively select low-fi sample points as well, the EI function based on the uncertainty coming from the low-fi kriging model should be formulated, which is almost a blank area so far and will be done in Section 3.