Skip to main content
Springer Nature Link
Log in

An approximate sequential optimization and reliability assessment method for reliability-based design optimization

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

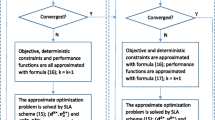
Sequential optimization and reliability assessment (SORA) is one of the most popular decoupled approaches to solve reliability-based design optimization (RBDO) problem because of its efficiency and robustness. In SORA, the double loop structure is decoupled through a serial of cycles of deterministic optimization and reliability assessment. In each cycle, the deterministic optimization and reliability assessment are performed sequentially and the boundaries of violated constraints are shifted to the feasible direction according to the reliability information obtained in the previous cycle. In this paper, based on the concept of SORA, approximate most probable target point (MPTP) and approximate probabilistic performance measure (PPM) are adopted in reliability assessment. In each cycle, the approximate MPTP needs to be reserved, which will be used to obtain new approximate MPTP in the next cycle. There is no need to evaluate the performance function in the deterministic optimization since the approximate PPM and its sensitivity are used to formulate the linear Taylor expansion of the constraint function. One example is used to illustrate that the approximate MPTP will approach the accurate MPTP with the iteration. The design variables and the approximate MPTP converge simultaneously. Numerical results of several examples indicate the proposed method is robust and more efficient than SORA and other common RBDO methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Aoues Y, Chateauneuf A (2010) Benchmark study of numerical methods for reliability-based design optimization. Struct Multidiscip Optim 41:277–294

    Article  MathSciNet  MATH  Google Scholar 

  • Chen D, Hasselman T, Neill D (1997) Reliability-based structural design optimization for practical applications. In: Proceeding of the 38thAIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and material conference, Kissimmee, AIAA-97-1403

  • Chen Z, Qiu H, Gao L, Su L, Li P (2013a) An adaptive decoupling approach for reliability-based structural optimization. Comput Struct 84(21):1353–1367

    Article  Google Scholar 

  • Chen Z, Qiu H, Gao L, Li P (2013b) An optimal shifting vector approach for efficient probabilistic design. Struct Multidiscip Optim 47(6):905–920

    Article  Google Scholar 

  • Cheng G, Xu L, Jiang L (2006) A sequential approximate programming stragety for reliability-based structural optimization and reliability assessment method. Struct Saf 33(1):42–50

    Google Scholar 

  • Cho TM, Lee BC (2011) Reliability-based design optimization using convex linearization and sequential optimization and reliability assessment method. Struct Saf 33(2011):42–50

    Article  Google Scholar 

  • Du X, Chen W (2004) Sequential optimization and reliability assessment method for efficient probabilistic design. J Mech Des 126(2):225–233

    Article  Google Scholar 

  • Frangopol DM, Corotis RB (1996) Reliability-based structural system optimization: state-of-the-art versus state-of-the-practice. Proc. 12th conference held in conjunction with structures congress XIV, 67–78

  • He Q, Li Y-S, Ao L-B, Wen Z-X, Yue Z-F (2011) Reliability and multidisciplinary design optimization for turbine blade based on single-loop method. J Propulsion Technol 32(5):658–663

    Google Scholar 

  • Ju BH, Lee BC (2008) Reliability-based design optimization using a moment method and a kriging metamodel. Eng Optim 40(5):421–438

    Article  MathSciNet  Google Scholar 

  • Lee JJ, Lee BC (2005) Efficient evaluation of probabilistic constraints using an envelope function. Eng Optim 37(2):185–200

    Article  Google Scholar 

  • Lee JO, Yang YS, Ruy WS (2002) A comparative study on reliability-index and target-performance-based probabilistic structural design optimization. Comput Struct 80:257–269

    Article  Google Scholar 

  • Liang J, Mourelatos ZP, Tu J (2004). A single-loop method for reliability-based design optimization. In: Proceedings of ASME design engineering technical conferences, paper N0DETC2004/DAC-57255

  • Liang J, Mourelatos ZP, Nikolaidis E (2007) A single-loop approach for system reliability-based design optimization. J Mech Des 129(12):1215–1224

    Article  Google Scholar 

  • Nguyen TH, Song J, Paulino GH (2010) Single-loop system reliability-based design optimization using matrix-based system reliability method: theory and applications. J Mech Des 132(1):0110051–01100511

    Article  Google Scholar 

  • Nikolaidis E, Burdisso R (1988) Reliability based optimization: a safety index approach. Comput Struct 28(6):781–788

    Article  MATH  Google Scholar 

  • Rackwitz R, Fiessler B (1978) Structural reliability under combined random load sequence. Comput Struct 9(5):489–494

    Article  MATH  Google Scholar 

  • Silva M, Tortorelli DA, Norato JA, Ha C, Bae HR (2010) Component and system reliability-based topology optimization using a single-loop method. Struct Multidiscip Optim 41(1):87–106

    Article  MathSciNet  MATH  Google Scholar 

  • Tu J, Choi KK, Park YH (1999) A new study on reliability based design optimization. J Mech Des 121(4):557–564

    Article  Google Scholar 

  • Wang L, Kodiyalam S (2002) An efficient method for probabilistic and robust design with non-normal distributions. In: Proceeding of the 43th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and material conference, Denver, AIAA-2002-1754

  • Wu YT, Wang W (1998) Efficient probabilistic design by converting reliability constraints to approximately equivalent deterministic constraints. J Integr Des Process Sci 2(4):13–21

    Google Scholar 

  • Wu YT, Millwater HR, Cruse TA (1990) Advanced probabilistic structural analysis method for implicit performance functions. AIAA J 28(9):1663–1669

    Article  Google Scholar 

  • Yang RJ, Gu L (2004) Experience with approximate reliability-based optimization methods. Struct Multidiscip Optim 26(2):152–159

    Article  MathSciNet  Google Scholar 

  • Yi P, Cheng GD (2008) Futher study on efficiency of sequential approximate programming for probabilistic structural design optimization. Struct Multidiscip Optim 35(6):509–522

    Article  MathSciNet  MATH  Google Scholar 

  • Youn BD, Choi KK (2004) An investigation of nonlinearity of reliability-based design optimization approaches. J Mech Des 126(5):403–411

    Article  Google Scholar 

  • Youn BD, Choi KK, Park YH (2003) Hybrid analysis method for reliability based design optimization. J Mech Des 125(3):221–232

    Article  Google Scholar 

  • Zhang X, Huang H, Xie M (2011) Single loop methods for reliability based design optimization. J Univ Electron Sci Technol China 40(1):157–160

    Google Scholar 

  • Zhuang XT, Pan R (2012) A sequential sampling strategy to improve reliability-based design optimization with implicit constraint functions. J Mech Des 134:0210021–02100210

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to deeply thank the anonymous reviewers for their useful and helpful comments and gratefully acknowledge the financial support provided by the National Natural Scientific Foundation of China (51479027) and the Key Project of Chinese National Programs for Fundamental Research and Development (2015CB057703).

Author information

Authors and Affiliations

  1. Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian, 116024, China

    Ping Yi, Zuo Zhu & Jinxin Gong

Authors
  1. Ping Yi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zuo Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jinxin Gong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zuo Zhu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yi, P., Zhu, Z. & Gong, J. An approximate sequential optimization and reliability assessment method for reliability-based design optimization. Struct Multidisc Optim 54, 1367–1378 (2016). https://doi.org/10.1007/s00158-016-1478-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-016-1478-2

Keywords

Profiles

  1. Zuo Zhu View author profile