Abstract
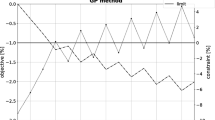
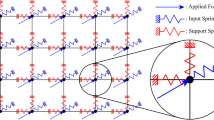
This paper proposes a modified gradient projection method (GPM) that can solve the structural topology optimization problem including density-dependent force efficiently. The particular difficulty of the considered problem is the non-monotonicity of the objective function and consequently the optimization problem is not definitely constrained. Transformation of variables technique is used to eliminate the constraints of the design variables, and thus the volume is the only possible constraint. The negative gradient of the objective function is adopted as the most promising search direction when the point is inside the feasible domain, while the projected negative gradient is used instead on condition that the point is on the hypersurface of the constraint. A rational step size is given via a self-adjustment mechanism that ensures the step size is a good compromising between efficiency and reliability. Furthermore, some image processing techniques are employed to improve the layouts. Numerical examples with different prescribed volume fractions and different load ratios are tested respectively to illustrate the characteristics of the topology optimization with density-dependent load.













Similar content being viewed by others
References
Ananiev S (2005) On equivalence between optimality criteria and projected gradient methods with application to topology optimization problem. Multibody Syst Dyn 13(1):25–38
Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O (2011) Efficient topology optimization in matlab using 88 lines of code. Struct Multidisc Optim 43(1):1–16
Arora J (2004) Introduction to optimum design. Academic Press
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202
Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications. Springer
Bourdin B (2001) Filters in topology optimization. Int J Numer Meth Eng 50(9):2143–2158
Bruyneel M, Duysinx P (2005) Note on topology optimization of continuum structures including self-weight. Struct Multidisc Optim 29(4):245–256
Bruyneel M, Duysinx P, Fleury C (2002) A family of mma approximations for structural optimization. Struct Multidisc Optim 24(4):263–276
Chang C, Borgart A, Chen A, Hendriks MA (2013) Direct gradient projection method with transformation of variables technique for structural topology optimization. Struct Multidisc Optim. doi:10.1007/s00158-013-0964-z
Fleury C (1989) Conlin: an efficient dual optimizer based on convex approximation concepts. Struct Optim 1(2):81–89
Hassani B, Hinton E (1999) Homogenization and structural topology optimization: theory, practice and software. Springer, London
Huang X, Xie YM (2010) A further review of eso type methods for topology optimization. Struct Multidisc Optim 41(5):671–683
Lopes RA, Stump FV, Silva ECN (2005) Topology optimization of three dimensional structures under self-weight and inertial forces. In: 6th world congress of structural and multidisciplinary optimization. Rio de Janeiro, Brazil, pp 5–6
Ma ZD, Kikuchi N, Hagiwara I (1993) Structural topology and shape optimization for a frequency response problem. Comput Mech 13(3):157–174
Nakamura H, Dow M, Rozvany G (1981) Optimal spherical cupola of uniform strenght: allowance for selfweigth. Arch Appl Mech 51(3):159–181
Park KS, Chang SY, Youn SK (2003) Topology optimization of the primary mirror of a multi-spectral camera. Struct Multidisc Optim 25(1):46–53
Pedersen NL (2000) Maximization of eigenvalues using topology optimization. Struct Multidisc Optim 20(1):2–11
Poulsen TA (2002) Topology optimization in wavelet space. Int J Numer Meth Eng 53(3):567–582
Rao SS (2009) Engineering optimization: theory and practice. Wiley
Rosen JB (1960) The gradient projection method for nonlinear programming. part i. linear constraints. J Soc Ind Appl Math 8(1):181–217
Rosen JB (1961) The gradient projection method for nonlinear programming. part ii. nonlinear constraints. J Soc Ind Appl Math 9(4):514–532
Rozvany G, Wang CM (1984) Optimal layout theory: allowance for selfweight. ASCE J Engng Mec 110(1):66–83
Rozvany G, Nakamura H, Kuhnell B (1980) Optimal archgrids: allowance for selfweight. Comput Method Appl M 24(3):287–304
Rozvany GI (1977) Optimal plastic design: allowance for self-weight. ASCE J Eng Mech Div 103(6):1165–1170
Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidisc Optim 33(4–5):401–424
Svanberg K (1987) The method of moving asymptotes—new method for structural optimization. Int J Numer Meth Eng 24(2):359–373
Svanberg K (1995) A globally convergent version of mma without linesearch. In: Proceedings of the first world congress of structural and multidisciplinary optimization, vol 28. Goslar, Germany, pp 9–16
Turteltaub S, Washabaugh P (1999) Optimal distribution of material properties for an elastic continuum with structure-dependent body force. Int J Solids Struct 36(30):4587–4608
Wang CM, Rozvany G (1983) On plane prager-structures i: non-parallel external loads and allowances for selfweight. Int J Mech Sci 25(7):529–541
Xu S, Cai Y, Cheng G (2010) Volume preserving nonlinear density filter based on heaviside functions. Struct Multidisc Optim 41(4):495–505
Zhu J, Beckers P, Zhang W (2007) On the layout design of multi-component systems. In: Zhang W, Beckers P (eds) Advancements in Design Optimization of Materials, Xi’an, China. International Workshop, pp 235–251
Zuo KT, Chen LP, Zhang YQ, Yang J (2005) A hybrid topology optimization algorithm for structural design. Eng Optim 37(8):849–866
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chang, C., Chen, A. The gradient projection method for structural topology optimization including density-dependent force. Struct Multidisc Optim 50, 645–657 (2014). https://doi.org/10.1007/s00158-014-1078-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-014-1078-y