Skip to main content
SpringerLink
Log in

Robust springback optimization of a dual phase steel seven-flange die assembly

  • Industrial Application
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

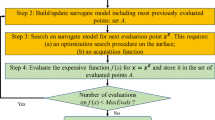
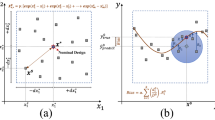
Abstract

This paper investigates robust springback optimization of a DP600 dual phase steel seven-flange die assembly composed of different flange designs. The optimum values of the die radius and the punch radius are sought to minimize the mean and the standard deviation of springback using surrogate based optimization. Springback values at the training points of surrogate models are evaluated using the finite element analysis code LS-DYNA. In this work, four different surrogate modeling types are considered: polynomial response surfaces (PRS) approximations, stepwise regression (SWR), radial basis functions (RBF) and Kriging (KR). Two sets of surrogate models are constructed in this study. The first set is constructed to relate the springback to the design variables as well as the random variables. It is found for the first set of surrogate models that KR provides more accurate springback predictions than PRS, SWR and RBF. The mean and the standard deviation of springback are calculated using Monte Carlo simulations, where the first set of surrogate models is utilized. The second set of surrogate models is generated to relate the mean and the standard deviation of springback to the design variables. It is found for the second set of surrogate models that PRS provides more accurate springback predictions than SWR, RBF and KR. It is also found that introducing beads increases the mean performance and the robustness. The robust optimization is performed and significant springback reductions are obtained for all flanges ranging between 7% and 85% compared to the nominal design. It is also found that a design change that decreases the mean springback also reduces the springback variation. It is observed that the optimization results heavily dependent on the bounds of the die and punch radii. In addition, optimization with multiple surrogates is investigated. Finding multiple candidates of optimum with multiple surrogates and selecting the one with the best actual performance is found to be a better strategy than optimizing using the most accurate surrogate model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Acar E, Guler MA, Gerçeker B, Cerit ME, Bayram B (2011) Multi-objective crashworthiness optimization of tapered thin-walled tubes with axisymmetric indentations. Thin-Walled Struct 49(1):94–105

    Article  Google Scholar 

  • Buhmann MD (2003) Radial basis functions: theory and implementations. Cambridge University Press, New York

    Book  MATH  Google Scholar 

  • Chen P, Koc M (2007) Simulation of springback variation in forming of advanced high strength steels. J Mater Process Technol 190:189–198

    Article  Google Scholar 

  • de Souza T, Rolfe BF (2010) Characterizing material and process variation effects on springback robustness for a semi-cylindrical sheet metal forming process. Int J Mech Sci 52:1756–1766

    Article  Google Scholar 

  • Du X, Venigella PK, Liu D (2009) Robust mechanism synthesis with random and interval variables. Mech Mach Theory 44:1321–1337

    Article  MATH  Google Scholar 

  • Finn MJ, Galbraith PC, Wu L, Hallquist JO, Lum L, Lin TL (1995) Use of a coupled explicit-implicit solver for calculating springback in automotive body panels. J Mater Process Technol 50:395–409

    Article  Google Scholar 

  • Glaz B, Goel T, Liu L, Friedmann PP, Haftka RT (2009) Multiple-Surrogate approach to helicopter rotor blade vibration reduction. AIAA J 47(1):271–282

    Article  Google Scholar 

  • Ingarao G, Di Lorenzo R, Micari F (2009) Analysis of stamping performances of dual phase steels: a multi-objective approach to reduce springback and thinning failure. Mater Des 30:4421–4433

    Article  Google Scholar 

  • Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13:455–492

    Article  MathSciNet  MATH  Google Scholar 

  • Li YQ, Cui ZS, Ruan XY, Zhang DJ (2005) Application of six sigma robust optimization in sheet metal forming. AIP Conf Proc 778:819–824

    Article  Google Scholar 

  • Liew K, Tan H, Ray T, Tan M (2004) Optimal process design of sheet metal forming for minimum springback via integrated neural network evolutionary algorithm. Struct Multidisc Optim 26:284–294

    Article  Google Scholar 

  • Lin Z, Liu G, Xu W, Bao Y (2000) Study on the effects of numerical parameters on the precision of springback prediction. In: Proceedings of the sixth international LS-DYNA users conference 5

  • Lophaven SN, Nielsen HB, Søndergaard J (2002) DACE-a MATLAB® kriging toolbox, informatics and mathematical modeling. Technical University of Denmark, Lyngby

    Google Scholar 

  • Marretta L, Ingarao G, Di Lorenzo R (2010) Design of sheet stamping operations to control springback and thinning: a multi-objective stochastic optimization approach. Int J Mech Sci 52:914–927

    Article  Google Scholar 

  • MATLAB® (2009) User’s guide and reference guide

  • Meinders T, Burchitz IA, Bonte MHA, Lingbeek RA (2008) Numerical product design: springback prediction, compensation and optimization, Int. J Mach Tools Manuf 48:499–514

    Article  Google Scholar 

  • Myers RH, Montgomery DC (2002) Response surface methodology: process and product optimization using designed experiments. Wiley, New York

    MATH  Google Scholar 

  • Naceur H, Guo YQ, Ben-Elechi S (2006) Response surface methodology for design of sheet forming parameters to control springback effects. Comput Struct 84:1651–1663

    Article  Google Scholar 

  • Naceur H, Ben-Elechi S, Batoz JL, Kropf-Lenoir C (2008) Response surface methodology for the rapid design of aluminum sheet metal forming parameters. Mater Des 29:781–790

    Article  Google Scholar 

  • Park JS (1994) Optimal Latin-hypercube designs for computer experiments. J Stat Plan Inference 39:95–111

    Article  MATH  Google Scholar 

  • Prior AM (1994) Applications of implicit and explicit finite element techniques to metal forming. J Mater Process Technol 45:649–656

    Article  Google Scholar 

  • Sacks J, Welch WJ, Mitchell TJ, Wynn HP (1989) Design and analysis of computer experiments. Stat Sci 4(4):409–435

    Article  MathSciNet  MATH  Google Scholar 

  • Strano M (2008) A technique for FEM optimization under reliability constraint of process variables in sheet metal forming. Int J Mater Form 1:13–20

    Article  Google Scholar 

  • Wang W, Hou B, Lin Z, Xia ZC (2009) An Engineering approach to improve the stamping robustness of high strength steels. J Manuf Sci Eng 131:1–5

    Google Scholar 

  • Wei L, Yuying Y, Zhongwen X, Lihong Z (2009) Springback control of sheet metal forming based on the response-surface method and multi-objective genetic algorithm. Mater Sci Eng 499:325–328

    Article  Google Scholar 

  • Zhang W, Shivpuri R (2008) Investigating reliability of variable blank holder force control in sheet drawing under process uncertainties. J Manuf Sci E-T ASME. doi:10.1115/1.2951936

    Google Scholar 

Download references

Acknowledgements

The authors greatly acknowledge the support provided by COŞKUNÖZ METAL FORM for sharing the experimental facilities, and thank Mustafa Yenice and Mesut Kaya of COŞKUNÖZ METAL FORM for their help in the experiments. Also, the financial support provided by the Scientific and Technological Research Council of Turkey (TÜBİTAK), under award MAG-109M078, is greatly acknowledged.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, TOBB University of Economics and Technology, Sogutozu Cad. No: 43, Sogutozu, Ankara, 06560, Turkey

    Deniz Bekar, Erdem Acar, Firat Ozer & Mehmet Ali Guler

Authors
  1. Deniz Bekar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Erdem Acar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Firat Ozer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mehmet Ali Guler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Erdem Acar.

Appendices

Appendix A: Sensitivity analysis

To investigate the effects of design and random variables on springback, a simple sensitivity analysis is performed. The variables as well as the springback values are normalized between 0 and 1. A linear PRS is fitted to the normalized springback in terms of normalized variables. The coefficients of the linear terms are indications of the sensitivity of springback to the variables. The coefficients are listed in Table 19 for θ 1 and in Table 20 for θ 2. The absolute values of the coefficients are listed in descending order in Table 21 for θ 1 and in Table 22 for θ 2. It is found that the punch radius is more influential than the die radius for θ 1, whereas the opposite is true for θ 2. Among the random variables, the hardening coefficient and the hardening exponent are found to be the most influential variables. Finally, the anisotropy coefficient R 90 is observed to have more influence than the other anisotropy coefficients R 0 and R 45.

Table 19 The sensitivity of θ 1 to the design variables and the random variables
Full size table
Table 20 The sensitivity of θ 2 to the design variables and the random variables
Full size table
Table 21 The sorted listings of the sensitivity of θ 1 to the design variables and the random variables
Full size table
Table 22 The sorted listings of the sensitivity of θ 2 to the design variables and the random variables
Full size table

Appendix B: Accuracy evaluation of the surrogate models of Flanges #2 through #7

The accuracy evaluation of the surrogate models of Flange #2 through #7 are listed in Tables 23, 24, 25, 26, 27, 28. SWR models show the best performance for Flange #4 θ 1 and θ 2. RBF model is the most accurate model for Flange #2 θ 1, Flange #3 θ 1, and Flange #7 θ 1. Kriging models show the best performance for Flange #2 θ 2, Flange #3 θ 2, Flange #5 θ 1 and θ 2, Flange #6 θ 1, Flange #7 θ 2. PRS models do not show superiority over other surrogate models for any of the responses.

Table 23 Accuracies of different surrogate models constructed for θ 1 and θ 2 (Flange #2)
Full size table
Table 24 Accuracies of different surrogate models constructed for θ 1 and θ 2 (Flange #3)
Full size table
Table 25 Accuracies of different surrogate models constructed for θ 1 and θ 2 (Flange #4)
Full size table
Table 26 Accuracies of different surrogate models constructed for θ 1 and θ 2 (Flange #5)
Full size table
Table 27 Accuracies of different surrogate models constructed for θ 1 and θ 2 (Flange #6)
Full size table
Table 28 Accuracies of different surrogate models constructed for θ 1 and θ 2 (Flange #7)
Full size table

Appendix C: Optimization results for Flanges #2 through #7

Table 29 presents a comparison of the mean and the standard deviation of springback for the nominal design (column 2, 3, and 9) and the optimum design (both the surrogate model prediction (column 4, 7, and 10) as well as the MCS results (column 5, 8, 11) at the found optimum).

Table 29 Optimization results for Flanges #3 through #7 (w 1 = w 2 = 0.5)
Full size table

For θ 1 minimization of Flange #3, optimum results are provided in Table 29 (rows 3 to 6, columns 3 to 5). The mean springback is reduced by 39% and the standard deviation of the springback is increased by about 16.4%. The optimum values of the die and punch radii are found to be 3 mm (lower bound of R d ) and 7.52 mm, respectively. For θ 2 minimization of Flange #3, optimum results are presented in Table 29 (rows 3 to 6, columns 6 to 8). It is observed that the mean springback is reduced by 49.5% and the standard deviation of the springback is increased by about 71.2%. The optimum values of the die and punch radii are both found to be 10 mm (upper bound of R d and R p ). For θ 1 + θ 2 minimization of Flange #3, optimum results are listed in Table 29 (rows 3 to 6, columns 9 to 11). It is found that the mean springback is reduced by 31.1% and the standard deviation of the springback is increased by about 4%. The optimum values of the die and punch radii are both found to be 10 mm (upper bound of R d and R p ), as in the case of θ 2 minimization.

For θ 1 minimization of Flange #4, optimum results are provided in Table 29 (rows 7 to 10, columns 3 to 5). The mean springback is reduced by 35.1% and the standard deviation of springback is maintained at its nominal value. The optimum value of the punch radius is found to be 6 mm, which is the lower bound of R p . For θ 2 minimization of Flange #4, optimum results are presented in Table 29 (rows 7 to 10, columns 6 to 8). It is observed that the mean springback is reduced by 7.4% and the standard deviation of the springback is decreased by about 2.3%. The optimum value of the punch radius is found to be 4 mm. For θ 1 + θ 2 minimization of Flange #4, optimum results are listed in Table 29 (rows 7 to 10, columns 9 to 11). It is found that the mean springback is reduced by 11.6% and the standard deviation of the springback is decreased by about 2.3%. The optimum value of the punch radius is found to be 6 mm (upper bound of R p ), as in the case of θ 1 minimization.

For θ 1 minimization of Flange #5, optimum results are provided in Table 29 (rows 11 to 14, columns 3 to 5). The mean springback is reduced by 85.7% and the standard deviation of the springback is increased by about 9%. The optimum values of the die and punch radii are found to be 9.53 mm and 10 mm (upper bound of R p ), respectively. For θ 2 minimization of Flange #5, optimum results are presented in Table 29 (rows 11 to 14, columns 6 to 8). It is observed that the mean springback is reduced by 14.9% and the standard deviation of the springback is reduced by about 7.6%. The optimum values of the die and punch radii are found to be 8.75 mm and 7.55 mm, respectively. For θ 1 + θ 2 minimization of Flange #5, optimum results are listed in Table 29 (rows 11 to 14, columns 9 to 11). It is found that the mean springback is reduced by 51.8% and the standard deviation of the springback is increased by about 39.7%. The optimum values of the die and punch radii are found to be 9.53 mm and 10 mm (upper bound of R p ), respectively, as in the case of θ 1 minimization.

For θ 1 minimization of Flange #6, optimum results are provided in Table 29 (rows 15 to 18, columns 3 to 5). The mean springback is maintained at its nominal value and the standard deviation of springback is reduced by about 98.6%. The optimum value of the punch radius is found to be 3 mm, which is the lower bound of R p .

For θ 1 minimization of Flange #7, optimum results are provided in Table 29 (rows 19 to 22, columns 3 to 5). The mean springback is reduced by 58.2% and the standard deviation of the springback is increased by about 9.7%. The optimum values of the die and punch radii are found to be 8.45 mm and 10 mm (upper bound of R p ), respectively. For θ 2 minimization of Flange #7, optimum results are presented in Table 29 (rows 19 to 22, columns 6 to 8). It is observed that the mean springback is reduced by 57.4% and the standard deviation of the springback is reduced by about 12%. The optimum values of the die and punch radii are found to be 8.38 mm and 4.04 mm, respectively. For θ 1 + θ 2 minimization of Flange #7, optimum results are listed in Table 29 (rows 19 to 22, columns 9 to 11). It is found that the mean springback is reduced by 36.1% and the standard deviation of the springback is increased by about 12.3%. The optimum values of the die and punch radii are found to be 8.45 mm and 10 mm (upper bound of R p ), respectively, as in the case of θ 1 minimization.

As noted earlier, we assumed that the weight coefficients are equal (w 1 = w 2 = 0.5). Predicted and actual optimum result will change with values of the w 1 and w 2. For example, if \(\mu_{\theta_1 } \) is more important than \(\sigma_{\theta_1 } \), then we would use w 1 > w 2 in optimization and we would obtain a smaller \(\mu_{\theta_1 } \) value than the \(\mu_{\theta_1 } \) value presented in Table 11. However, there is a trade-off. If w 1 is larger than the w 2, the \(\sigma_{\theta_1 } \) will be larger than the \(\sigma _{\theta_1 } \) value evaluated at equal weight coefficients (w 1 = w 2 = 0.5). That is, determining the weight coefficients is up to designer. Designer’s performance expectation from a system is important to decide whether w 1 must be larger than w 2 or not. The same assessment can be made for the results of Flanges #2 through #7.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bekar, D., Acar, E., Ozer, F. et al. Robust springback optimization of a dual phase steel seven-flange die assembly. Struct Multidisc Optim 46, 425–444 (2012). https://doi.org/10.1007/s00158-012-0771-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-012-0771-y

Keywords

Search

Navigation