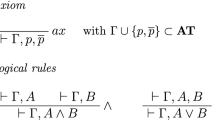A note on cut-elimination for classical propositional logic

Abstract

In Schwichtenberg (Studies in logic and the foundations of mathematics, vol 90, Elsevier, pp 867–895, 1977), Schwichtenberg fine-tuned Tait’s technique (Tait in The syntax and semantics of infinitary languages, Springer, pp 204–236, 1968) so as to provide a simplified version of Gentzen’s original cut-elimination procedure for first-order classical logic (Gallier in Logic for computer science: foundations of automatic theorem proving, Courier Dover Publications, London, 2015). In this note we show that, limited to the case of classical propositional logic, the Tait–Schwichtenberg algorithm allows for a further simplification. The procedure offered here is implemented on Kleene’s sequent system G4 (Kleene in Mathematical logic, Wiley, New York, 1967; Smullyan in First-order logic, Courier corporation, London, 1995). The specific formulation of the logical rules for G4 allows us to provide bounds on the height of cut-free proofs just in terms of the logical complexity of their end-sequent.

1 Introduction

In [5], Schwichtenberg fine-tuned Tait’s technique [7] so as to provide a simplified version of Gentzen’s original cut-elimination procedure, which notoriously requires a complex induction on a certain lexicographic order [2]. In particular, Schwichtenberg showed that termination of the cut-elimination procedure can be achieved by resorting to two independent inductions on $\omega$. The Reduction Lemma is proved by induction on the sum of the heights of the two derivations delivering the premises of the cut-application under consideration [5, Lemma 2.6, p. 874] and the final Hauptsatz is proved by induction on the cut-rank of the whole proof [5, Theorem 2.7, p. 875].

In this note we show that, limited to the case of classical propositional logic, cut-elimination allows for a further simplification. As a matter of fact, the proof of Lemma 4 (our Reduction Lemma) is simply led by cases, whereas Theorem 5 (the Hauptsatz) is proved by a double induction on the cut-size of proofs and on the number of maximal cut-applications. The size of a cut-application is just defined as the number of connectives occurring in one of its premises. Accordingly, the cut-size of a proof $\pi$ is defined as the supremum of all the cut-sizes relating to $\pi$.

The algorithm proposed in this note is tailored on the sequent system $\mathsf {GS4}$, the one-sided formulation à la Tait of Kleene’s $\mathsf {G4}$ [3, 6]. The procedure heavily relies on the fact that, for any non-atomic formula A, if the sequent $\vdash \Gamma ,A$ is provable in $\mathsf {GS4}$, then it is also provable by means of a particular proof in which A occurs as the principal formula in the last inference step (Lemma 3). The main advantage of dealing with Kleene’s system $\mathsf {GS4}$ lies in the fact that the height of cut-free proofs turns out to be bounded by the number of occurrences of logical connectives in their end-sequent (Theorem 6). Moreover, we prove that any two cut-free proofs ending in the same sequent have always the same height (Theorem 7).

2 Preliminary notions and results

Following [7], we limit ourselves to considering only two connectives: conjunction ($\wedge$) and disjunction ($\vee$). In formal languages à la Tait, negation comes as primitive on atomic sentences and it extends to compound formulas by means of the following equivalences:

$$\begin{aligned} \overline{\overline{A}}\Leftrightarrow A\qquad \overline{A\wedge B}\Leftrightarrow \overline{A}\vee \overline{B}\qquad \overline{A\vee B}\Leftrightarrow \overline{A}\wedge \overline{B} \end{aligned}$$

The set $\mathcal {F}$ of well-formed formulas is defined accordingly:

$$\begin{aligned} \mathcal {F}::=\mathbf {AT}\,|\,\mathcal {F}\wedge \mathcal {F}\,|\,\mathcal {F}\vee \mathcal {F}. \end{aligned}$$

Logical contexts $\Gamma ,\Delta ,\ldots$ are taken to be multisets of formulas from $\mathcal {F}$. As usual, we write $\Gamma ,A$ and $\Gamma ,\Delta$ to mean the two multisets $\Gamma \uplus [A]$ and $\Gamma \uplus \Delta$, respectively. We write $\{\Gamma \}$ to indicate the set collecting the elements of $\Gamma$.

We call $\mathsf {GS4}$ the one-sided version of Kleene’s sequent system G4 whose rules are displayed in Fig. 1 [1, 3, 4, 6]. The height $h(\pi )$ of a proof $\pi$ is given by the number of sequents occurring in one of its longest branches. A subproof $\delta$ of a proof $\pi$ is said to be direct in case $\delta$ ends in one of the premises of $\pi$’s last inference. Moreover, we recall that any application of the logical rules displays a principal formula in the conclusion: the formula whose principal connective has been introduced by the very inference step under consideration.

Definition 1

The complexity $\mathcal {C}(A)$ of a formula A is given by the number of occurrences of logical connectives in A. More formally: $\mathcal {C}(A)=0$, for any $A\in \mathbf {AT}$, and $\mathcal {C}(A\wedge B)=\mathcal {C}(A\vee B)=\mathcal {C}(A)+\mathcal {C}(B)+1$. For any multiset $\Gamma =[A_{1},A_{2},\ldots ,A_{n}]$, we set $\mathcal {C}(\Gamma )=\mathcal {C}(A_{1})+\mathcal {C}(A_{2})+\cdots +\mathcal {C}(A_{n})$.

Remark 1

For any multiset of formulas $\Gamma ,C$, we have $\mathcal {C}(\Gamma ,C)=\mathcal {C}(\Gamma ,\overline{C})$.

Observe that, in the specific formulation adopted here, instances of the ax-rule must be clauses, i.e., sequents in which only atomic formulas from $\mathbf {AT}$ are displayed. The next proposition shows that such a linguistic restriction does not affect provability.

Proposition 1

$\mathsf {GS4}$ proves the sequent $\vdash \Gamma ,p,\overline{p}$, for any multiset of formulas $\Gamma$, and any $p\in \mathbf {AT}$.

Fig. 1

The rules of the sequent calculus $\mathsf {GS4}$

Proof

We proceed by induction on $\mathcal {C}(\Gamma )$. If $\mathcal {C}(\Gamma )=0$, then $\vdash \Gamma ,p,\overline{p}$ is already an instance of the ax-rule. As for $\mathcal {C}(\Gamma )>0$, we distinguish two cases:

• $\Gamma =\Gamma ',A\wedge B$. By inductive hypothesis, there are two $\mathsf {GS4}$-proofs $\delta$ and $\rho$ ending in $\vdash \Gamma ',A,p,\overline{p}$ and $\vdash \Gamma ',B,p,\overline{p}$, respectively. The two proofs $\delta$ and $\rho$ can be then composed by means of an application of the $\wedge$-rule so as to finally get the conclusion $\vdash \Gamma ',A\wedge B,p,\overline{p}$.

• $\Gamma =\Gamma ',A\vee B$. Similar to the previous case. $\square$

Below, we recall the well-known fact that the structural rule of Weakening is admissible in $\mathsf {GS4}$ (cfr, for instance, [5, Lemma 2.3.1, p. 873]):

Lemma 2

(Weakening admissibility) If $\mathsf {GS4}$ proves $\vdash \Gamma$, then it also proves the sequent $\vdash \Gamma ,A$, for any formula A.

Proof

Let $\pi$ be a $\mathsf {GS4}$-proof ending in $\vdash \Gamma$. Once the formula A is uniformly added to all the sequents occurring in $\pi$, each of $\pi$’s top sequents $\vdash \Gamma ,p,\overline{p}$ is turned into the sequent $\vdash \Gamma ,A,p,\overline{p}$ which is, by Proposition 1, provable. $\square$

Notation

Given a $\mathsf {GS4}$-proof $\pi$ of $\vdash \Gamma$ and a formula A, we denote with $\mathcal {W}(\pi ,A)$ the $\mathsf {GS4}$-proof of $\vdash \Gamma ,A$ obtained from $\pi$ according to the procedure employed in the proof of Lemma 2. If $A\in \Gamma$, then $\mathcal {W}(\pi ,A)=\pi$.

The following lemma states a peculiar property of the $\mathsf {GS4}$ system which will prove crucial to attain the results proposed in the next section. Such a property comes as a byproduct of the fact that $\mathsf {GS4}$ logical rules are all reversible in the sense that provability of the conclusion always implies provability of the premise(s) (cfr. [5, Lemma 2.5, p. 873]).

Lemma 3

(Height-preserving permutability) Assume there is a $\mathsf {GS4}$-proof $\pi$ of  $\vdash \Gamma ,A$ with $\mathcal {C}(A)>0$. The sequent $\vdash \Gamma ,A$ is also provable by means of a proof $\rho$ such that: (i) the formula A occurs as principal in $\rho$’s last inference, and (ii) $h(\pi )=h(\rho )$.

Proof

If $\mathcal {C}(\Gamma )=0$, then $\pi$’s last rule must be already the one introducing A’s principal connective and so $\rho =\pi$. Otherwise, we proceed by showing that any proof $\pi$ of $\vdash \Gamma ,A$ can be turned into a proof $\rho$ of $\vdash \Gamma ,A$ having the desired form, simply by permuting downwards along $\pi$ the specific instance of the logical rule introducing A’s principal connective. The proof is led by induction on $\mathcal {C}(\Gamma ,A)$. We shall be considering the following four possible situations.

• $A\equiv B\wedge C$ and $\pi$’s last rule is a $\wedge$-rule. Let $D\wedge E$ be the formula occurring as principal in $\pi$’s last inference, and $\pi _{1}$ and $\pi _{2}$ the two direct subproofs of $\pi$ ending in $\vdash \Gamma ,B\wedge C,D$ and $\vdash \Gamma ,B\wedge C,E$, respectively. By inductive hypothesis, there is a proof $\pi '$ shaped as displayed below, such that $h(\pi _{1})=max(h(\pi _{\langle 1,1\rangle }),h(\pi _{\langle 1,2\rangle }))+1$ and $h(\pi _{2})=max(h(\pi _{\langle 2,1\rangle }),h(\pi _{\langle 2,2\rangle }))+1$.

  

  The proof $\pi '$ can be then rearranged into the proof $\rho$ reported below, simply by interchanging the two final applications of the logical rules.

  

  We finally observe that:

  $$\begin{aligned} \begin{array}{lll} h(\pi ) &{} = &{} max(h(\pi _1),h(\pi _2))+1= \\ &{} = &{} max(max(h(\pi _{\langle 1,1\rangle }),h(\pi _{\langle 1,2\rangle }))+1,max(h(\pi _{\langle 2,1\rangle }),h(\pi _{\langle 2,2\rangle }))+1)+1 \\ &{} = &{} max(h(\pi _{\langle 1,1\rangle }),h(\pi _{\langle 1,2\rangle }),h(\pi _{\langle 2,1\rangle }), h(\pi _{\langle 2,2\rangle }))+2 \\ &{} = &{} max(max(h(\pi _{\langle 1,1\rangle }),h(\pi _{\langle 2,1\rangle }))+1,max(h(\pi _{\langle 1,2\rangle }),h(\pi _{\langle 2,2\rangle }))+1)+1 \\ &{} = &{} h(\rho ) \\ \end{array} \end{aligned}$$

• $A\equiv B\vee C$ and $\pi$’s last rule is a $\wedge$-rule. Let $D\wedge E$ be the formula occurring as principal in $\pi$’s last inference, and $\pi _{1}$ and $\pi _{2}$ the two direct subproofs of $\pi$ ending in $\vdash \Gamma ,B\vee C,D$ and $\vdash \Gamma ,B\vee C,E$, respectively. By inductive hypothesis, there is a proof $\pi '$ shaped as indicated below, such that $h(\pi _{1})=h(\pi _{1}')+1$ and $h(\pi _{2})=h(\pi _{2}')+1$.

  

  We interchange the two final applications of the logical rules so as to obtain the proof $\rho$ reported below.

  

  Since $h(\pi )=max(h(\pi _{1}),h(\pi _{2}))+1$, we also have $h(\pi )=max(h(\pi _{1}')+1,h(\pi _{2}')+1)+1$, thence $h(\pi )=max(h(\pi _{1}'),h(\pi _{2}'))+2=h(\rho )$.

• $A\equiv B\wedge C$ and $\pi$’s last rule is a $\vee$-rule. Let $D\vee E$ be the formula occurring as principal in $\pi$’s last inference and $\pi _{1}$ the direct subproof of $\pi$ ending in $\vdash \Gamma ,B\wedge C,D,E$. By inductive hypothesis, there is a proof $\pi '$ shaped as indicated below and such that $h(\pi _{1})=max(h(\pi _{\langle 1,1\rangle }),h(\pi '_{\langle 1,2\rangle }))+1$.

  

  The proof $\rho$ can be obtained from $\pi '$ be interchanging the two final applications of the logical rules as indicated below.

  

  Since, $h(\pi )=h(\pi _{1})+1$, we also have $h(\pi )=max(h(\pi '_{\langle 1,1\rangle }),h(\pi '_{\langle 1,2\rangle }))+2= max(h(\pi '_{\langle 1,1\rangle })+1,h(\pi '_{\langle 1,2\rangle })+1)+1=h(\rho )$.

• $A\equiv B\vee C$ and $\pi$’s last rule is a $\vee$-rule. Let $D\vee E$ be the formula occurring as principal in $\pi$’s last inference and $\pi _{1}$ the direct subproof of $\pi$ ending in $\vdash \Gamma ,B\vee C,D,E$. By inductive hypothesis, there is a proof $\pi '$ shaped as indicated below and such that $h(\pi _{1})=h(\pi '_{1})+1$.

  

  The derivation $\pi '$, in turn, can be easily rewritten into the derivation $\rho$ by interchanging the two final applications of the $\vee$-rule as indicated below.

  

We finally observe that $h(\pi )=h(\pi _{1})+1=h(\pi _{1}')+2=h(\rho )$. $\square$

Notation

Given a $\mathsf {GS4}$-proof $\pi$ of $\vdash \Gamma ,A$ with $\mathcal {C}(A)>0$, we denote with $\mathcal {P}(\pi ,A)$ the proof of $\vdash \Gamma ,A$ whose last inference is the one introducing A’s principal connective. The proof $\mathcal {P}(\pi ,A)$ is intended to be obtained from $\pi$ according to the procedure indicated in the proof of Lemma 3. For $A\equiv B\wedge C$, we indicate with $\mathcal {P}(\pi ,A)_{\mathtt {L}}$ and $\mathcal {P}(\pi ,A)_{\mathtt {R}}$ the two direct subproofs of $\mathcal {P}(\pi ,A)$ ending in $\vdash \Gamma ,B$ and $\vdash \Gamma ,C$, respectively.

3 The cut-elimination algorithm

We call $\mathsf {GS4}^{+}$ the system obtained by adding to the rules of $\mathsf {GS4}$ the cut-rule in its additive one-sided formulation:

When the situation requires it, we will point at specific applications of the cut-rule by adding a subscript $i\in \mathbb {N}$ to the label ‘cut’.

Before going into the details of the cut-elimination algorithm, we need to introduce some key notions to provide a suitable measure for the ‘quantity of cut’ present in a derivation.

Definition 2

The size of a cut-application

is taken to equal the complexity of the multiset of formulas displayed in one of its premises, i.e., $|cut_{i}|=\mathcal {C}(\Gamma ,C)=\mathcal {C}(\Gamma ,\overline{C})$ (cfr. Remark 1). Let $\big \{cut_{1}, cut_{2}, \ldots ,cut_{n}\big \}$ be a complete enumeration of the cut-applications occurring in a $\mathsf {GS4}^{+}$-proof $\pi$. The cut-size of $\pi$ is defined as $|\pi |=max\big \{|cut_{i}|+1 : 1\leqslant i\leqslant n\big \}$. If $\pi$ is cut-free, then $|\pi |=0$. A cut-application $cut_{i}$ is said to be maximal in $\pi$ whenever $|cut_{i}|=|\pi |-1$.

Lemma 4

(Reduction Lemma) Any $\mathsf {GS4}^{+}$-proof $\pi$ of $\vdash \Gamma$ displaying exactly one cut-application can be turned into a $\mathsf {GS4}^{+}$-proof $\pi '$ of the same sequent and such that $|\pi '|<|\pi |$.

Proof

We can limit ourselves to considering a proof $\pi$ whose unique cut-application occurs as $\pi$’s last rule without any loss of generality. Let $\delta$ and $\rho$ be the two direct subproofs of $\pi$ ending in the two premises of the cut-application under consideration:

Since $\pi$ contains exactly one cut-application, we immediately have that: (i) both $\delta$ and $\rho$ are cut-free, and (ii) $|\pi |=\mathcal {C}(\Gamma ,C)+1= \mathcal {C}(\Gamma ,\overline{C})+1$.

If $|\pi |=1$, then the premises of the cut-application are both introduced as instances of the ax-rule; say $C\equiv p$, for some atomic sentence $p\in \mathbf {AT}$. It is easy to see that either $\Gamma =\Gamma ',p,\overline{p}$ or $\Gamma =\Gamma ',q,\overline{q}$ for some $q\in \mathbf {AT}$. Thence, the proof $\pi$ can be simply rewritten as follows:

If $|\pi |>1$, we need to proceed by cases and subcases as follows.

• [Case 1] For $\mathcal {C}(C)>0$, we consider the two following subcases according to whether C’s principal connective is a conjunction or a disjunction. Both of them are treated by means of a two-step reduction. The first step (indicated by $\Longrightarrow$) is an application of Lemma 3 aiming at permuting downwards the logical rules introducing the principal connective of the cut-formulas C and $\overline{C}$. The second step (indicated by $\longrightarrow$) comes as a standard parallel reduction.

  • [Case 1.1] If $C\equiv A\wedge B$, then we proceed as follows:

    

    

    By definition, $|cut|=\mathcal {C}(\Gamma ,A\wedge B)$, $|cut_{1}|=\mathcal {C}(\Gamma ,A,\overline{B})$, and $|cut_{2}|=\mathcal {C}(\Gamma ,\overline{B})$. Since $\mathcal {C}(B)=\mathcal {C}(\overline{B})$, we can conclude that $|cut_{2}|\leqslant |cut_{1}|<|cut|$.

  • [Case 1.2] $C\equiv A\vee B$. Symmetric with respect to the previous one.

• [Case 2] If $\mathcal {C}(C)=0$, since $\mathcal {C}(\Gamma )>0$, there will be a formula $D\in \Gamma$ such that $\mathcal {C}(D)>0$. We need now to distinguish two subcases according to whether D’s principal connective is a conjunction or a disjunction. As for the previous case, we provide a list of two-step reductions. The first reduction ($\Longrightarrow$) is still an application of Lemma 3 which allows us to permute downward the logical rule introducing the principal connective of D. By performing the second step ($\longrightarrow$) we permute upwards the cut-application under consideration.

  • [Case 2.1] $D\equiv A\vee B$

    

    Since $|cut|=\mathcal {C}(\Gamma ,A\wedge B,p)$ and $|cut_{1}|=\mathcal {C}(\Gamma ,A,B,p)$, we have that $|cut_{1}|<|cut|$.

  • [Case 2.2] $D\equiv A\wedge B$

    

    

    

    In this case we have $|cut|=\mathcal {C}(\Gamma ,A\wedge B,p)$, $|cut_{1}|=\mathcal {C}(\Gamma ,A,p)$, and $|cut_{2}|=\mathcal {C}(\Gamma , B,p)$. Therefore, $|cut_{1}|<|cut|$ and $|cut_{2}|<|cut|$. $\square$

We are now ready to apply the Reduction Lemma to finally prove the following theorem:

Theorem 5

(Hauptsatz) Any $\mathsf {GS4}^{+}$-proof $\pi$ of $\vdash \Gamma$ can be turned into a $\mathsf {GS4}$-proof $\pi '$ ending in the same sequent.

Proof

The proof is led by a double induction: the principal one is on $|\pi |$, whereas the side induction is on the number of maximal cut-applications. If $|\pi |=1$, then we just keep reducing the topmost cut-applications as indicated in the proof of Lemma 4 till a completely cut-free derivation is achieved.

If $|\pi |>1$, we consider an arbitrarily selected topmost maximal cut-application $cut_{i}$. Let $\delta$ be the subproof of $\pi$ whose last inference is the cut-application under consideration. In particular, let $\delta _{1}$ and $\delta _{2}$ denote the two direct subproofs of $\delta$ ending in the two premises of $cut_{i}$:

Since $cut_{i}$ occurs as a topmost maximal cut-application, we have $|\delta _{1}|,|\delta _{2}|<|\pi |$. By inductive hypothesis, there are two $\mathsf {GS4}$-proofs $\delta '_{1}$ and $\delta '_{2}$ ending in $\vdash \Delta ,C$ and $\vdash \Delta ,\overline{C}$, respectively. Consider now the proof $\delta '$ obtained from $\delta$ by replacing $\delta _{1}$ with $\delta _{1}'$ and $\delta _{2}$ with $\delta _{2}'$:

By Lemma 4, there is a $\mathsf {GS4}^{+}$-proof $\delta ''$ ending in $\vdash \Delta$ and such that $|\delta ''|<|\delta |$.

Let $\pi _{1}$ be the proof obtained from $\pi$ by replacing the subproof $\delta$ with $\delta ''$. The proofs $\pi _{1}$ and $\pi$ end in the same sequent, but $\pi _{1}$ contains one maximal cut-application less than $\pi$. So, it suffices to keep focussing on topmost maximal cut-applications and reiterate the procedure till a proof $\pi _{k}$ of $\vdash \Gamma$ such that $|\pi _{k}|<|\pi |$ is finally achieved. At this point, our inductive hypothesis guarantees the existence of a cut-free proof $\pi '$ ending in $\vdash \Gamma$. $\square$

Remark 2

(First-order logic) The following rules for quantifiers prove reversible in the sense already specified [8].

Unfortunately, this fact doesn’t mean that the technical machinery deployed in this section can be straightforwardly extended so as to prove cut-elimination for the whole first-order system. The reason is simple: for any instance of the $\exists$-rule in which A(t) is non-atomic, $\mathcal {C}(\Gamma ,\exists xA,A[{}^{x}\!/_{t}])>\mathcal {C}(\Gamma ,\exists xA)$.

4 Bounds

One of the main advantages of dealing with Kleene’s system $\mathsf {GS4}$ lies in the fact that the height of cut-free proofs turns out to be bounded by the complexity of their end-sequent. In particular:

Theorem 6

For any $\mathsf {GS4}$-proof $\pi$ ending in $\vdash \Gamma$, $h(\pi )\leqslant \mathcal {C}(\Gamma )+1$.

Proof

We proceed by induction on $\mathcal {C}(\Gamma )$. If $\mathcal {C}(\Gamma )=0$, then $\pi$ is just an instance of the ax-rule and so $h(\pi )=1$. In case $\mathcal {C}(\Gamma )>0$, we need to distinguish the following two cases.

• The last inference in $\pi$ is an application of the $\wedge$-rule. With $\pi _{1}$ and $\pi _{2}$ we refer to the two direct subproofs of $\pi$ ending in $\vdash \Gamma ,A$ and $\vdash \Gamma ,B$, respectively. By inductive hypothesis, $h(\pi _{1})\leqslant \mathcal {C}(\Gamma ,A)+1$ and $h(\pi _{2})\leqslant \mathcal {C}(\Gamma ,B)+1$. Since $h(\pi )=max(h(\pi _{1}),h(\pi _{2}))+1$, we can finally conclude that $h(\pi )\leqslant \mathcal {C}(\Gamma ,A\wedge B)+1$.

• The last inference in $\pi$ is an application of the $\vee$-rule. Let $\pi _{1}$ be the direct subproof of $\pi$ ending in $\vdash \Gamma ,A,B$. By inductive hypothesis, $h(\pi _{1})\leqslant \mathcal {C}(\Gamma ,A,B)+1$. It is also the case that $\mathcal {C}(\Gamma ,A\vee B)=\mathcal {C}(\Gamma ,A,B)+1$. We then conclude that $h(\pi )=h(\pi _{1})+1\leqslant \mathcal {C}(\Gamma ,A,B)+2=\mathcal {C}(\Gamma ,A\vee B)+1$. $\square$

A further fact can be also established:

Theorem 7

If $\pi$ and $\rho$ are two $\mathsf {GS4}$-proofs ending in the same sequent $\vdash \Gamma$, then $h(\pi )=h(\rho )$.

Proof

We proceed by induction on $\mathcal {C}(\Gamma )$. If $\mathcal {C}(\Gamma )=0$, then $\vdash \Gamma$ is just an instance of the ax-rule and so $\pi =\rho$. If $\mathcal {C}(\Gamma )>0$, then there is a multiset $\Gamma '$ and a formula A such that $\Gamma =\Gamma ',A$ with $\mathcal {C}(A)>0$. We distinguish the following two cases:

• $A\equiv B\wedge C$. Consider the two proofs $\pi '$ (the one on the right) and $\rho '$ (the one on the left) displayed below.

  

  By inductive hypothesis, $h(\mathcal {P}(\pi ,B\wedge C)_{\mathtt {L}})= h(\mathcal {P}(\rho ,B\wedge C)_{\mathtt {L}})$ and $h(\mathcal {P}(\pi ,B\wedge C)_{\mathtt {R}})=h(\mathcal {P}(\rho ,B\wedge C)_{\mathtt {R}})$, thence $h(\pi ')=h(\rho ')$. Moreover, by Lemma 3, $h(\pi )=h(\pi ')$ and $h(\rho )=h(\rho ')$. The combination of these facts allows us to conclude that $h(\pi )=h(\rho )$.

• $A\equiv B\vee C$. Similar to the previous case.$\square$