Abstract
We study the problem of embedding arbitrary \({\mathbb {Z}}^k\)-actions into the shift action on the infinite dimensional cube \(\left( [0,1]^D\right) ^{{\mathbb {Z}}^k}\). We prove that if a \({\mathbb {Z}}^k\)-action X satisfies the marker property (in particular if X is a minimal system without periodic points) and if its mean dimension is smaller than D / 2 then we can embed it in the shift on \(\left( [0,1]^D\right) ^{{\mathbb {Z}}^k}\). The value D / 2 here is optimal. The proof goes through signal analysis. We develop the theory of encoding \({\mathbb {Z}}^k\)-actions into band-limited signals and apply it to proving the above statement. Main technical difficulties come from higher dimensional phenomena in signal analysis. We overcome them by exploring analytic techniques tailored to our dynamical settings. The most important new idea is to encode the information of a tiling of \({\mathbb {R}}^k\) into a band-limited function which is constructed from another tiling.







Similar content being viewed by others
Notes
When \(k=2\), it might be better to call x a discrete image.
More generally, we can prove that if an aperiodic dynamical system satisfies the small boundary property then it satisfies the marker property. The small boundary property is a notion introduced by Lindenstrauss–Weiss [LW00, Definition 5.2], and it is satisfied by every aperiodic finite dimensional system. We do not use these facts. So we omit a detailed explanation.
Strictly speaking, the paper [LT14] considered only the case of \(k=1\). But their construction can be generalized to \({\mathbb {Z}}^k\)-actions without any changes.
This fact is not used in the paper. So here we describe only the outline of the proof. Readers may skip this footnote. We first note that \({\mathcal {B}}_1(a_1,\dots ,a_k)\) admits not only the shift action \(\sigma \) of \({\mathbb {Z}}^k\) but also the action of the bigger group \({\mathbb {R}}^k\). In particular every lattice \(\Lambda \subset {\mathbb {R}}^k\) naturally acts on it. The mean dimension of this \(\Lambda \)-action is given by \(\mathrm {mdim}({\mathcal {B}}_1(a_1,\dots ,a_k),\Lambda ) = \left| {\mathbb {R}}^k/\Lambda \right| \mathrm {mdim}({\mathcal {B}}_1(a_1,\dots ,a_k),\sigma )\), where \(\sigma \) is the shift action of \({\mathbb {Z}}^k\) and \(\left| {\mathbb {R}}^k/\Lambda \right| \) is the volume of the fundamental domain of \(\Lambda \). Let \(\Lambda = \{(b_1 n_1,\dots , b_k n_k)|\, n_1,\dots ,n_k\in {\mathbb {Z}}\}\) with \(a_i b_i < 1\). By the sampling theorem (Lemma 2.4), there exists a \(\Lambda \)-equivariant embedding from \({\mathcal {B}}_1(a_1,\dots , a_k)\) to \([-1,1]^\Lambda \). So \(\mathrm {mdim}({\mathcal {B}}_1(a_1,\dots ,a_k),\Lambda ) \le 1\). On the other hand, for a sufficiently small \(\varepsilon >0\) and a lattice \(\Gamma = \{(c_1 n_1,\dots , c_k n_k)|\, n_1,\dots , n_k\in {\mathbb {Z}}\}\) with \(a_i c_i >1\), an interpolation construction (cf. Section 4) shows that there exists a \(\Gamma \)-equivariant embedding from \([-\varepsilon , \varepsilon ]^\Gamma \) to \({\mathcal {B}}_1(a_1,\dots , a_k)\). So \(\mathrm {mdim}({\mathcal {B}}_1(a_1,\dots ,a_k),\Gamma ) \ge 1\). Therefore \((c_1\dots c_k)^{-1} \le \mathrm {mdim}({\mathcal {B}}_1(a_1,\dots ,a_k),\sigma ) \le (b_1\dots b_k)^{-1}\). Letting \(b_i\rightarrow a_i^{-1}\) and \(c_i\rightarrow a_i^{-1}\), we get the conclusion.
Of course this is over-simplified. Signal analysis is a mutli-faceted discipline and cannot be classified as a sub-area of complex analysis. For example, we emphasized its communication theory aspect in Section 1.1. But the complex analysis viewpoint is convenient here.
Here we state a (seemingly) simpler version of the theorem for clarifying the argument, but indeed this statement is equivalent to Lemma 2.4.
A point \(p\in {\mathbb {C}}^k\) is a zero point of \(f:{\mathbb {C}}^k\rightarrow {\mathbb {C}}^k\) if \(f(p)=0\). Notice that the domain and target of f have the same dimension. Therefore generically zero points of f are expected to be isolated.
If readers do not know the definition of topological dimension, then they may think that this is the definition of topological dimension. Only one nontrivial point is that \(\dim X\) is a topological invariant whereas \(\mathrm {Widim}_\varepsilon (X,d)\) depends on the distance d. The proof goes as follows: Let \(d'\) be another distance on X. For any \(\delta >0\) there is \(\varepsilon >0\) such that \(d(x,y)<\varepsilon \Rightarrow d'(x,y) < \delta \). Then \(\mathrm {Widim}_\delta (X,d') \le \mathrm {Widim}_\varepsilon (X,d)\). This shows that \(\lim _{\varepsilon \rightarrow 0}\mathrm {Widim}_\varepsilon (X,d)\) is independent of d.
The subadditivity follows from the fact that the map
$$\begin{aligned} (X,d_{\Omega _1\cup \Omega _2}) \rightarrow (X\times X, d_{\Omega _1}\times d_{\Omega _2}), \quad x\mapsto (x,x) \end{aligned}$$is an isometric embedding, where \(d_{\Omega _1}\times d_{\Omega _2}\left( (x_1,x_2),(y_1,y_2)\right) = \max \left( d_{\Omega _1}(x_1,y_1), d_{\Omega _2}(x_2,y_2)\right) \). The invariance follows from the fact that the map \(T^a: (X,d_{a+\Omega })\rightarrow (X,d_{\Omega })\) is an isometry.
When \(k=1\), this is just a calculus exercise to show that if a nonnegative sequence \(\{a_n\}\) satisfies \(a_{m+n}\le a_m+a_n\) then the limit of \(a_n/n\) exists. The argument for \(k>1\) is a straightforward generalization.
Let \(\Delta \subset P\) be a simplex of vertexes \(v_0,\dots , v_k\). Then its relative interior is the set of points \(\lambda _0 v_0 + \dots +\lambda _k v_k\) where \(\lambda _0, \dots , \lambda _k>0\) and \(\sum _{i=0}^k \lambda _i =1\). In particular the relative interior of a vertex \(\{v\}\) is equal to \(\{v\}\) itself. Every point of P belongs to the relative interior of some simplex.
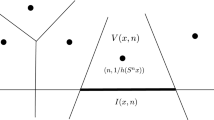
More precisely, for \(\varepsilon >0\) and for each \(x\in X\) and \(n\in {\mathbb {Z}}^k\) with \(\mathrm {Int}\, W_{0}(x,n)\ne \emptyset \), if \(y\in X\) is sufficiently close to x, then the Hausdorff distance between \(W_{0}(x,n)\) and \(W_{0}(y,n)\) is smaller than \(\varepsilon \).
A Voronoi tiling generated by a discrete set \(A\subset {\mathbb {R}}^{k}\) is a partitioning of \({\mathbb {R}}^{k}\) into regions based on the closest distance to points in A. For more details, see Section 5.3.
It might look that \(M_1\) and h are also parameters. But we can choose them to be functions ofM. Namely for each natural number M we fix a natural number \(M_1=M_1(M)\) and a continuous function \(h= h_M:X\rightarrow [0,1]\) satisfying (5.6). Then only M remains to be a parameter.
The above explanation does not feature Condition (2). But indeed this is a very important condition. It did not appear in the paper [GT]. A substantial amount of the argument in this section has been developed for establishing this condition.
References
J. Auslander. Minimal Flows and Their Extensions. North-Holland, Amsterdam (1988).
Collected works of Arne Beurling, Vol. 2, Harmonic Analysis, Edited by L. Carleson, P. Malliavan, J. Neuberger, and J. Wermer, Birkhäuser, Boston-Basel-Berlin (1989)
M. Cornalba and B. Shiffman. A couterexample to the “Transcendental Bezout Problem”. Ann. Math., 96 (1972), 402–406
T.M. Cover and J.A. Thomas. Elements of Information Theory, second edition, Wiley, New York (2006).
H. Dym and H.P. McKean. Fourier Series and Integrals. Academic Press, New York-London (1972).
M. Gromov. Topological invariants of dynamical systems and spaces of holomorphic maps: I. Math. Phys. Anal. Geom., 2 (1999), 323–415.
Y. Gutman. Mean dimension and Jaworski-type theorems. Proc. Lond. Math. Soc., (4)111 (2015), 831–850.
Y. Gutman, E. Lindenstrauss and M. Tsukamoto. Mean dimension of \({\mathbb{Z}}^k\)-actions. Geom. Funct. Anal., (3)26 (2016), 778–817.
Y. Gutman and M. Tsukamoto. Embedding minimal dynamical systems into Hilbert cubes, preprint, arXiv:1511.01802.
W.K. Hayman. Meromorphic Functions. Clarendon Press, Oxford (1964).
W. Hurewicz and H. Wallman. Dimension Theory, Princeton University Press, Princeton (1941).
A. Hatcher. Algebraic Topology. Cambridge University Press, Cambridge (2002).
A. Jaworski. Ph.D. Thesis, University of Maryland (1974).
S.J. Lightwood. Morphisms from non-periodic \({\mathbb{Z}}^2\)-subshifts. I. Constructing embeddings from homomorphisms. Ergodic Theory Dyn. Syst., 23 (2003), 587–609.
S.J. Lightwood. Morphisms from non-periodic \({\mathbb{Z}}^2\) subshifts. II. Constructing homomorphisms to square-filling mixing shifts of finite type. Ergodic Theory Dyn. Syst., 24 (2004), 1227–1260.
E. Lindenstrauss. Mean dimension, small entropy factors and an embedding theorem. Inst. Hautes Études Sci. Publ. Math., 89 (1999), 227–262.
E. Lindenstrauss and M. Tsukamoto. Mean dimension and an embedding problem: an example. Israel J. Math., 199 (2014), 573–584.
E. Lindenstrauss and B. Weiss. Mean topological dimension. Israel J. Math., 115 (2000), 1–24.
J. Noguchi and J. Winkelmann. Nevanlinna Theory in Several Complex Variables and Diophantine Approximation. Springer, Tokyo (2014).
A. Olevskii and A. Ulanovskii. On multi-dimensional sampling and interpolation. Anal. Math. Phys., 2 (2012), 149–180.
L. Schwartz. Théorie des distributions. Hermann, Paris (1966).
C.E. Shannon. A mathematical theory of communication. Bell Syst. Tech. J., 27 (1948), 379–423, 623–656.
E.H. Spanier. Algebraic Topology. Springer, New York (1966).
Acknowledgements
This paper was written when the third named author stayed in the Einstein Institute of Mathematics in the Hebrew University of Jerusalem. He would like to thank the institute for its hospitality. The authors thank the referees for their many useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Y.G. was partially supported by the Marie Curie Grant PCIG12-GA-2012-334564 and the National Science Center (Poland) Grants 2013/08/A/ST1/00275 and 2016/22/E/ST1/00448. The corresponding author Y.Q. was partially supported by NNSF of China (11371339 and 11571335). M.T. was supported by John Mung Program of Kyoto University
Rights and permissions
About this article
Cite this article
Gutman, Y., Qiao, Y. & Tsukamoto, M. Application of signal analysis to the embedding problem of \({\mathbb {Z}}^k\)-actions. Geom. Funct. Anal. 29, 1440–1502 (2019). https://doi.org/10.1007/s00039-019-00499-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-019-00499-z
Keywords and phrases
- Band-limited signal
- Dynamical system
- \({\mathbb {Z}}^k\)-action
- Mean dimension
- Embedding
- Tiling of \({\mathbb {R}}^k\)