Global Stabilization for a Class of Stochastic High-Order Feedforward Nonlinear Systems Via Homogeneous Domination Approach

Abstract

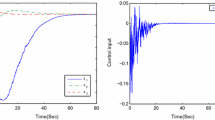
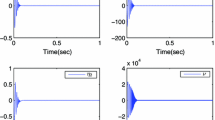
For a class of more general stochastic high-order feedforward nonlinear systems, this paper deals with the problem of state feedback stabilization. By introducing an appropriate coordinate transformation, the original system is transformed into an equivalent one with tunable gain. After that, by reasonably extending the homogeneous domination approach and skillfully choosing the low gain scale, a state feedback controller is explicitly constructed to render the closed-loop system globally asymptotically stable in probability. Two numerical examples are provided to demonstrate the effectiveness of the proposed design method.

Appendix

Proof of Lemma 7

(i) We first prove $r_{n}+\tau \ge \max _{1\le i\le n}\{2r_{i}\}$. By $r_{1}=1, r_{i+1}=\frac{r_{i}+\tau }{p}$, one has

$$\begin{aligned} r_i=\frac{p^{i-1}-1}{p^i-p^{i-1}}\tau +\frac{1}{p^{i-1}},\quad i=2,\ldots ,n. \end{aligned}$$

(29)

when $i=1$, choosing $d_1=\frac{(2p^{n-1}-1)(p-1)}{p^n-1}$ and $\tau \ge d_1$, with (29) and $p\in R_\mathrm{odd}^{>2}$, one can obtain

$$\begin{aligned} r_n+\tau \ge \frac{p^n-1}{p^n-p^{n-1}}d_1+\frac{1}{p^{n-1}} =2r_1. \end{aligned}$$

(30)

For $i=2,\ldots ,n$, choosing $d_i=\frac{(\frac{2}{p^{i-1}}-\frac{1}{p^{n-1}})(p-1)}{p-2+\frac{2}{p^{i-1}}-\frac{1}{p^{n-1}}}$ and $\tau \ge d_i$, by (29) and $p\in R_\mathrm{odd}^{>2}$, one gets

$$\begin{aligned} r_n+\tau\ge & {} \frac{p-2+\frac{2}{p^{i-1}}-\frac{1}{p^{n-1}}}{p-1}d_i+\frac{1}{p^{n-1}}-\frac{2}{p^{i-1}}+\frac{2-\frac{2}{p^{i-1}}}{p-1}\tau +\frac{2}{p^{i-1}}\nonumber \\= & {} 2r_i. \end{aligned}$$

(31)

It is easy to conclude that $d_1>1, 0<d_i<1, i=2,\ldots ,n$. By (30) and (31), $r_{n}+\tau \ge \max _{1\le i\le n}\{2r_{i}\}$ holds for any $p\in R_\mathrm{odd}^{>2}$ and $\tau \in [d_1,+\infty )$.

(ii) For any $p\in R_\mathrm{odd}^{>2}$ and $\tau \in [d_1,+\infty )$, one can choose $l_1$ to satisfy $r_{n}+\tau \ge \max _{1\le i\le n}\{\frac{r_{i}+\tau }{l_1}\}$.

From (i) and (ii), it follows that $r_{n}+\tau \ge \max _{1\le i\le n}\{2r_{i}, \frac{r_{i}+\tau }{l_1}\}$. According to the denseness of real number, there exists $\mu \in R_\mathrm{odd}^{+}$ such that $r_{n}+\tau \ge \mu \ge \max _{1\le i\le n}\{2r_{i}, \frac{r_{i}+\tau }{l_1}\}$ holds for any $p\in R_\mathrm{odd}^{>2}$ and $\tau \in [d_1,+\infty )$. $\square$

Proof of Lemma 8

We first prove that $V_{i}(\eta _1,\ldots ,\eta _{i})$ is ${\mathcal {C}}^2$. By (10) and (12), it is easy to obtain

$$\begin{aligned}&\frac{\partial U_{i}}{\partial \eta _{i}}=\zeta _{i}^{\frac{q_{i}}{\mu }},\quad \frac{\partial ^2U_{i}}{\partial \eta _{i}^2}=\frac{q_{i}}{r_i}\eta _i^{\frac{\mu -r_i}{r_i}} \zeta _{i}^{\frac{q_{i}}{\mu }-1}, \quad \frac{\partial ^2U_{i}}{\partial \eta _{i}\partial \eta _{j}}=\frac{\partial ^2U_{i}}{\partial \eta _{j}\partial \eta _{i}}=-\frac{q_{i}}{\mu } \frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}} \zeta _{i}^{\frac{q_{i}}{\mu }-1},\nonumber \\&\quad \frac{\partial U_{i}}{\partial \eta _{j}} =-\frac{q_{i}}{\mu }\frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}}\int _{\eta _{i}^{*}}^{\eta _{i}}\left( s^{\frac{\mu }{r_{i}}}-{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{q_{i}}{\mu }-1}\hbox {d}s, \quad \frac{\partial ^2 U_{i}}{\partial \eta _{j}^2}=-\frac{q_{i}}{\mu }\frac{\partial ^2{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}^2}\cdot \nonumber \\&\quad \int _{\eta _{i}^{*}}^{\eta _{i}}\left( s^{\frac{\mu }{r_{i}}}-{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{q_{i}}{\mu }-1}\hbox {d}s +\frac{q_{i}(q_{i}-\mu )}{\mu ^2}\left( \frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}}\right) ^2\int _{\eta _{i}^{*}}^{\eta _{i}} \left( s^{\frac{\mu }{r_{i}}}-{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{q_{i}}{\mu }-2}\hbox {d}s,\nonumber \\&\quad \frac{\partial ^2 U_{i}}{\partial \eta _{j}\partial \eta _{k}}= \frac{\partial ^2 U_{i}}{\partial \eta _{k}\partial \eta _{j}}= \frac{q_{i}(q_{i}-\mu )}{\mu ^2}\frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}}\frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{k}}\int _{\eta _{i}^{*}}^{\eta _{i}} \left( s^{\frac{\mu }{r_{i}}}-{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{q_{i}}{\mu }-2}\hbox {d}s, \end{aligned}$$

(32)

where $j,k=1,\ldots ,i-1$ and the last equality is obtained by using $\frac{\partial ^2{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}\partial \eta _{k}}=0, j\ne k$. By $\mu \ge \max _{1\le i\le n}\{2r_{i}, \frac{r_{i}+\tau }{l_1}\}$, $\frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}}=-\beta _{i-1}\cdots \beta _j \frac{\mu }{r_j}\eta _j^{\frac{\mu -r_j}{r_j}}$ and $\frac{\partial ^2{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}^2}=-\beta _{i-1}\cdots \beta _j \frac{\mu (\mu -r_j)}{r_j^2}\eta _j^{\frac{\mu -2r_j}{r_j}}$, one has $\frac{q_{i}}{\mu }-2\ge 0, \frac{\mu -r_j}{r_j}\ge 1$ and $\frac{\mu -2r_j}{r_j}\ge 0$, from which and (32), we know that $V_i$ is ${\mathcal {C}}^2$.

Next, we divide into two cases to prove that $V_{i}(\eta _1,\ldots ,\eta _i)$ is positive definite and proper.

Case I When $\eta _{i}^{*}\le \eta _{i}$, using Lemma 5, one leads to

$$\begin{aligned} U_i(\eta _1,\ldots ,\eta _i)\ge & {} \frac{2^{\frac{q_{i}}{\mu }}}{2^{\frac{q_{i}}{r_i}}} \int _{\eta _{i}^{*}}^{\eta _{i}}(s-\eta _{i}^{*})^{\frac{q_{i}}{r_i}}\hbox {d}s \ge \frac{2^{\frac{q_{i}}{\mu }}r_i}{2^{\frac{q_{i}}{r_i}}(4l_1\mu -\tau )} (\eta _{i}-\eta _{i}^{*})^{\frac{4l_1\mu -\tau }{r_{i}}}. \end{aligned}$$

(33)

Case II When $\eta _{i}^{*}\ge \eta _{i}$, (33) can be proved similarly.

Therefore, $V_i=V_{i-1}(\eta _1,\ldots ,\eta _{i-1})+U_{i}(\eta _1,\ldots ,\eta _{i})\ge V_{i-1}(\eta _1,\ldots ,\eta _{i-1})+m_{i}(\eta _{i}-\eta _{i}^{*})^{\frac{4l_1\mu -\tau }{r_{i}}}$, which implies that $V_i(\bar{\eta }_i)$ is positive definite and proper, where $m_{i}$ is a positive constant.

At last, we prove inequality (13). From (3), (10)–(12) and (32), it follows that

$$\begin{aligned} {\mathcal {L}}V_{i}\le & {} -\ell \sum _{j=1}^{i-1}c_{i-1,j}\zeta _j^{4l_1} +\ell \zeta _{i}^{\frac{q_{i}}{\mu }}\eta _{i+1}^{p} +\ell \zeta _{i-1}^{\frac{q_{i-1}}{\mu }}(\eta _{i}^{p}-\eta _{i}^{*p})\nonumber \\&-\frac{q_{i}}{\mu }\ell \sum _{j=1}^{i-1} \frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}}\eta _{j+1}^{p} \int _{\eta _{i}^{*}}^{\eta _{i}}\left( s^{\frac{\mu }{r_{i}}}-{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{q_{i}}{\mu }-1}\hbox {d}s. \end{aligned}$$

(34)

We concentrate on the last two terms on the right-hand side of (34).

When $\frac{r_{i}p}{\mu }\le 1$, using (10) and Lemma 5, one obtains

$$\begin{aligned} |\eta _{i}^{p}-\eta _{i}^{*p}|= & {} \left| \left( \eta _{i}^{\frac{\mu }{r_{i}}}\right) ^{\frac{r_{i}p}{\mu }}-\left( {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{r_{i}p}{\mu }}\right| \le 2^{1-\frac{r_{i}p}{\mu }}|\zeta _{i}|^{\frac{r_{i}p}{\mu }}. \end{aligned}$$

(35)

when $\frac{r_{i}p}{\mu }\ge 1$, by (10) and Lemmas 4, 6, there exist positive constants c, $b_{i1}$ and $\bar{b}_{i1}$ such that

$$\begin{aligned} |\eta _{i}^{p}-\eta _{i}^{*p}|\le & {} c|\zeta _{i}|\left| \zeta _{i}^{\frac{r_{i}p}{\mu }-1} +(\beta _{i-1}\zeta _{i-1})^{\frac{r_{i}p}{\mu }-1}\right| \nonumber \\\le & {} b_{i1}|\zeta _{i-1}|^{\frac{r_{i}p}{\mu }}+\bar{b}_{i1}|\zeta _{i}|^{\frac{r_{i}p}{\mu }}. \end{aligned}$$

(36)

Combining (35) and (36), by Lemma 4, one has

$$\begin{aligned} \left| \zeta _{i-1}^{\frac{q_{i-1}}{\mu }}(\eta _{i}^{p}-\eta _{i}^{*p})\right|\le & {} |\zeta _{i-1}|^{\frac{q_{i-1}}{\mu }} \left( b_{i1}|\zeta _{i-1}|^{\frac{r_{i}p}{\mu }} +\tilde{b}_{i1}|\zeta _{i}|^{\frac{r_{i}p}{\mu }}\right) \nonumber \\\le & {} l_{i,i-1,1}\zeta _{i-1}^{4l_1}+\rho _{i1}\zeta _{i}^{4l_1}, \end{aligned}$$

(37)

where $\tilde{b}_{i1}=\max \{2^{1-\frac{r_{i}p}{\mu }},\bar{b}_{i1}\}$, $l_{i,i-1,1}$ and $\rho _{i1}$ are positive constants.

With the help of (10) and Lemmas 4 and 5, one obtains

$$\begin{aligned}&\left| -\frac{q_{i}}{\mu }\sum _{j=1}^{i-1} \frac{\partial {\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}}{\partial \eta _{j}}\eta _{j+1}^{p} \int _{\eta _{i}^{*}}^{\eta _{i}}\left( s^{\frac{\mu }{r_{i}}}-{\eta _{i}^{*}}^{\frac{\mu }{r_{i}}}\right) ^{\frac{q_{i}}{\mu }-1}\hbox {d}s\right| \nonumber \\&\quad \le \bar{d}\sum _{j=1}^{i-1}|\eta _j|^{\frac{\mu }{r_j}-1}|\eta _{j+1}|^{p} |\zeta _i|^{\frac{4l_1\mu -\tau }{\mu }-1}\nonumber \\&\quad \le \tilde{d}\sum _{j=1}^{i-1}\left( |\zeta _j|^{1-\frac{r_j}{\mu }}+ |\zeta _{j-1}|^{1-\frac{r_j}{\mu }}\right) |\zeta _i|^{\frac{4l_1\mu -\tau }{\mu }-1} \left( |\zeta _{j+1}|^{\frac{\tau +r_{j}}{\mu }} +|\zeta _{j}|^{\frac{\tau +r_{j}}{\mu }}\right) \nonumber \\&\quad \le \sum _{j=1}^{i-1}l_{ij2}\zeta _{j}^{4l_1}+\rho _{i2}\zeta _{i}^{4l_1}, \end{aligned}$$

(38)

where $\bar{d}, \tilde{d}, l_{ij2} (j=1,\ldots ,i-1)$ and $\rho _{i2}$ are positive constants.

Choosing

$$\begin{aligned} \eta _{i+1}^*= & {} -\beta _{i}^{\frac{r_{i+1}}{\mu }}\zeta _{i}^{\frac{r_{i+1}}{\mu }}, \quad \beta _i=(c_{ii}+\rho _{i1}+\rho _{i2})^{\frac{\mu }{r_{i+1}p}}, \quad \ c_{ii}>0, \nonumber \\ c_{ij}= & {} \bigg \{\begin{array}{ll}c_{i-1,j}-l_{ij2}>0,&{} \quad j=1,\ldots ,i-2,\\ c_{i-1,i-1}-l_{i,i-1,1}-l_{i,i-1,2}>0,&{} \quad j=i-1, \end{array} \end{aligned}$$

(39)

and substituting (37)–(39) into (34), the inequality (13) holds. $\square$