Abstract.
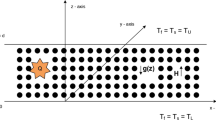
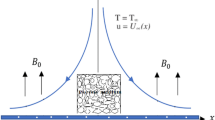
The nonlinear theory of the Kelvin-Helmholtz instability is employed to analyze the instability phenomenon of two ferrofluids through porous media. The effect of both magnetic field and mass and heat transfer is taken into account. The method of multiple scale expansion is employed in order to obtain a dispersion relation for the first-order problem and a Ginzburg–Landau equation, for the higher-order problem, describing the behavior of the system in a nonlinear approach. The stability criterion is expressed in terms of various competing parameters representing the mass and heat transfer, gravity, surface tension, fluid density, magnetic permeability, streaming, fluid thickness and Darcy coefficient. The stability of the system is discussed in both theoretically and computationally, and stability diagrams are drawn.
Similar content being viewed by others
Author information
Authors and Affiliations
Additional information
Received: July 25, 2002; revised: April 16, 2003
Rights and permissions
About this article
Cite this article
Moatimid, G.M. Nonlinear Kelvin-Helmholtz instability of two miscible ferrofluids in porous media. Z. angew. Math. Phys. 57, 133–159 (2005). https://doi.org/10.1007/s00033-005-2067-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00033-005-2067-1