Topological Loops with Decomposable Solvable Multiplication Groups

Abstract

In this paper we deal with the class $\mathcal {C}$ of decomposable solvable Lie groups having dimension six. We determine those Lie groups in $\mathcal {C}$ and their subgroups which are the multiplication groups Mult(L) and the inner mapping groups Inn(L) for three-dimensional connected simply connected topological loops L. This result completes the classification of the at most 6-dimensional solvable multiplication Lie groups of the loops L. Moreover, we obtain that every at most 3-dimensional connected topological proper loop having a solvable Lie group of dimension at most six as its multiplication group is centrally nilpotent of class two.

1 Introduction

The notion of the multiplication group Mult(L) and the inner mapping group Inn(L) of a loop L was introduced and firstly investigated by A. A. Albert and R. H. Bruck. Since their papers [1, 2] much work has been done to study the correspondences between the structure of the loop L and that of the groups Mult(L) and Inn(L). In particular many results relate nilpotency and solvability of loops to the analogous properties of their groups Mult(L) and Inn(L) ([13, 19, 22, 24, 26]). M. Niemenmaa and T. Kepka established in [20] the necessary and sufficient conditions for a group G to be the multiplication group of L. In their criteria the existence of special transversals A and B with respect to a subgroup K of G plays an important role. These transversals belong to the sets of left and right translations of L whereas K corresponds to the inner mapping group of L. For finite loops the importance of the permutation groups Mult(L) and Inn(L) as well as the connected transversals A and B is documented in many papers (cf. [3, 4, 16, 18, 21, 25]).

Topological and differentiable loops are investigated thoroughly by P. T. Nagy and K. Strambach in [17] as continuous and differentiable sections in Lie groups. Part II of [17] is devoted to the explicit description and determination of topological and smooth loops on low dimensional manifolds. Following their approach this article is a contribution to the study of connected topological loops L of dimension 3 having a solvable Lie group as their multiplication group. Each 2-dimensional connected topological proper loop having a Lie group as its multiplication group has nilpotency class two (cf. [5]). This nilpotency property is valid for 3-dimensional connected topological loops L having either a solvable Lie group of dimension at most 5 or a 6-dimensional indecomposable solvable Lie group as their group Mult(L) (cf. [7, 8, 10, 11]). Furthermore, in the class of the at most 5-dimensional solvable non-nilpotent Lie groups only decomposable groups occur as the multiplication group of L (cf. [7]). In this paper we show that the centrally nilpotency of class two property is satisfied for 3-dimensional topological loops L if the group Mult(L) is a 6-dimensional decomposable solvable Lie group (cf. Propositions 3, 6).

The multiplication groups and the inner mapping groups of the connected simply connected topological loops L with $\hbox {dim}(L)=3$ in the class of the solvable indecomposable Lie groups of dimension at most 6 are known (cf. [8, 9, 11]). Theorems 1, 2 and Proposition 5 complete the classification of the groups Mult(L) and Inn(L) for every solvable Lie group of dimension at most 6.

After the presentation of the necessary concepts, Proposition 2 shows that the decomposable solvable Lie groups of dimension 6 with discrete centre are not the multiplication group of a 3-dimensional connected topological loop. In section 4, respectively in 5 we treat the decomposable solvable Lie groups having a 1-dimensional, respectively a 2-dimensional centre. Among the 6-dimensional decomposable solvable Lie groups with 1-dimensional centre there are 18 families of Lie groups which are multiplication groups of 3-dimensional connected simply connected topological loops L. In the class of the 6-dimensional decomposable solvable Lie groups with 2-dimensional centre 9 families can be represented as the group Mult(L) of L. All these Lie groups have 3-dimensional commutator subgroups (see Corollary 2) and depend on at most two real parameters.

2 Preliminaries

A set L with a binary operation $(x,y) \mapsto x \cdot y$ is called a loop if there exists an element $e \in L$ such that $x=e \cdot x=x \cdot e$ holds for all $x \in L$ and for each $x \in L$ the left translations $\lambda _x:L \rightarrow L, \lambda _x (y)=x \cdot y$ and the right translations $\rho _x:L \rightarrow L$, $\rho _x(y)=y \cdot x$ are bijections of L. A loop L is proper if it is not a group. The maps $(x,y) \mapsto x \backslash y=\lambda _x^{-1}(y)$, respectively $(x,y) \mapsto y /x= \rho _x^{-1}(y)$, $x,y \in L$ are further binary operations on L. The permutation group $Mult(L)=\langle \lambda _x, \rho _x; x \in L \rangle$ is called the multiplication group of L. The inner mapping group Inn(L) of L is the stabilizer of the identity element $e \in L$ in Mult(L).

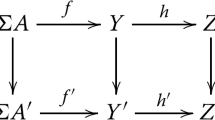
Let G be a group, let K be a subgroup of G, and let A and B be two left transversals to K in G. We say that A and B are K-connected if $a^{-1}b^{-1}ab \in K$ for every $a \in A$ and $b \in B$. The core $Co_G(K)$ of K in G is the largest normal subgroup of G contained in K. If L is a loop, then $\Lambda (L) = \{\lambda _x; x \in L\}$ and $P(L) =\{\rho _x; x \in L\}$ are Inn(L)-connected transversals in the group Mult(L). Theorem 4.1 in [20] states the following necessary and sufficient conditions for a group G to be the multiplication group of a loop L:

Proposition 1

A group G is isomorphic to the multiplication group of a loop if and only if there exists a subgroup K with $Co_G(K) = 1$ and K-connected left transversals A and B satisfying $G =\langle A, B \rangle$.

The kernel of a homomorphism $\alpha :(L, \cdot ) \rightarrow (L', *)$ of a loop L into a loop $L'$ is a normal subloop N of L. The centre Z(L) of a loop L consists of all elements z which satisfy the equations $z x \cdot y=z \cdot x y, \ x \cdot y z=x y \cdot z, \ x z \cdot y=x \cdot z y, \ z x =x z$ for all $x,y \in L$. If we put $Z_0=e$, $Z_1=Z(L)$ and $Z_i/Z_{i-1}=Z(L/Z_{i-1})$, then we obtain a series of normal subloops of L. If $Z_{n-1}$ is a proper subloop of L but $Z_n=L$, then L is centrally nilpotent of class n.

A loop L is called classically solvable if there exists a series $\{e\}=L_0 \le L_1 \le \dots \le L_n=L$ of subloops of L such that for every $i=1,2, \cdots ,n$, $L_{i-1}$ is normal in $L_{i}$ and each factor loop $L_{i}/L_{i-1}$ is a commutative group.

We often use the following Lemma which is proved in Theorems 3, 4 and 5 of [1], in Lemma 1.3, IV.1 of [2], in Lemma 2.3 of [8] and in Proposition 2.7 of [20].

Lemma 1

Let L be a loop with multiplication group Mult(L), inner mapping group Inn(L) and identity element e.

• 1. Let $\alpha$ be a homomorphism of the loop L onto the loop $\alpha (L)$ with kernel N. Then $\alpha$ induces a homomorphism of the group Mult(L) onto the group $Mult(\alpha (L))$. The set $M(N)=\{ m \in Mult(L); \ x N=m(x) N \ \hbox {for all} \ x \in L \}$ is a normal subgroup of Mult(L) containing the multiplication group Mult(N) of the loop N and the multiplication group of the factor loop L/N is isomorphic to Mult(L)/M(N).

• 2. For every normal subgroup $\mathcal {N}$ of Mult(L) the orbit $\mathcal {N}(e)$ is a normal subloop of L and $\mathcal {N} \le M(\mathcal {N}(e))$.

• 3. The core of Inn(L) in Mult(L) is trivial and the normalizer of Inn(L) in Mult(L) is the direct product $Inn(L) \times Z$, where Z is the centre of the group Mult(L).

A loop L is called topological if L is a topological space and the binary operations $(x,y) \mapsto x \cdot y, \ (x,y) \mapsto x \backslash y, (x,y) \mapsto y/x :L \times L \rightarrow L$ are continuous. In general the multiplication group of a topological loop L is a topological transformation group that does not have a natural (finite dimensional) differentiable structure. We investigate a 3-dimensional connected topological loop having a solvable Lie group as its multiplication group. The first assertion of the following lemma is proved in [12], IX.1, the second assertion is showed in [7], Lemma 5.

Lemma 2

For each connected topological loop there is a unique universal covering loop L. If L is a 3-dimensional connected simply connected topological loop having a solvable Lie group as its multiplication group, then it is homeomorphic to $\mathbb R^3$.

The elementary filiform Lie group ${\mathcal F}_{n}$ is the simply connected nilpotent Lie group of dimension $n \ge 3$ whose Lie algebra is elementary filiform, i.e. it has a basis $\{ e_1, \cdots , e_{n} \}$ with $[e_1, e_i]= e_{i+1}$ for $2 \le i \le n-1$. A 2-dimensional simply connected topological loop $L_{\mathcal F}$ is called an elementary filiform loop if its multiplication group is an elementary filiform group ${\mathcal F}_{n}$ of dimension $n \ge 4$ ([6]).

A Lie algebra is called decomposable, if it is the direct sum of two proper ideals. In this paper we assume that the multiplication group of L is a 6-dimensional solvable decomposable Lie group or a nilpotent decomposable Lie group of dimension $\le 5$. The next lemma summarizes the known results about the 3-dimensional topological loops having solvable decomposable Lie groups as their multiplication groups (cf. Lemmata 3.4, 3.5, 3.6 and Propositions 3.7, 3.8 in [6], pp. 390-393, Theorem 11 in [1], Theorem 6, Sections 4 and 5 in [7], Propositions 2.6, 2.7 in [8], Lemma 6 (d) in [11], Chapter I in [2]) which are often used in the paper.

Lemma 3

Let L be a 3-dimensional proper connected simply connected topological loop such that its multiplication group Mult(L) is a 6-dimensional solvable decomposable Lie group.

• a) The centre Z of the group Mult(L) and the centre $Z(L)=Z(e)$ of the loop L, where e is the identity element of L, are isomorphic. Moreover, the centre Z has dimension $\le 2$.

• b) The loop L is classically solvable and it has a 1-dimensional connected normal subloop N. Every such subloop N of L is isomorphic to $\mathbb R$ and lies in a 2-dimensional connected normal subloop M of L. The factor loop L/M is isomorphic to $\mathbb R$, whereas the loop M and the factor loop L/N are isomorphic either to the Lie group $\mathbb R^2$ or to the 2-dimensional non-abelian Lie group ${\mathcal L}_2$ or to an elementary filiform loop $L_{\mathcal F}$.

• c) If Mult(L) has discrete centre, then for every normal subloop $N \cong \mathbb R$ of L the factor loop L/N is isomorphic either to the group ${\mathcal L}_2$ or to a loop $L_{\mathcal F}$. The group Mult(L) has a normal subgroup S containing $Mult(N) \cong \mathbb R$ such that the factor group Mult(L)/S is isomorphic to the direct product ${\mathcal L}_2 \times {\mathcal L}_2$ if $L/I(e) \cong {\mathcal L}_2$, or to an elementary filiform Lie group ${\mathcal F}_{n}$, $n=4, 5$ if $L/I(e) \cong L_{\mathcal F}$. The normal subloop M containing N is isomorphic either to $\mathbb R^2$ or to ${\mathcal L}_2$ or to $L_{\mathcal F}$. The group Mult(L) has a normal subgroup V such that the orbit V(e) is the loop M, $Mult(L)/V \cong \mathbb R$, V contains the inner mapping group Inn(L) of L, the group Mult(M) of M and the commutator subgroup of Mult(L).

• d) If $\hbox {dim} (Z(L))=1$, then for every normal subloop $N \cong \mathbb R$ of L we have one of the following possibilities:

  • (i) The factor loop L/N is isomorphic to $\mathbb R^2$. Then L is centrally nilpotent of class 2, N coincides with the centre Z(L) of L and the group Mult(L) is a semidirect product of the normal subgroup $P=Z \times Inn(L) \cong \mathbb R^4$ by a group $Q \cong \mathbb R^2$ such that the orbit P(e) is Z(L).

  • (ii) The factor loop L/N is isomorphic either to the Lie group ${\mathcal L}_2$ or to a loop $L_{\mathcal F}$. Then case c) is fulfilled. In particular, if $N=Z(L)$, then M is not isomorphic to the group ${\mathcal L}_2$.

• e) If $\hbox {dim} (Z(L))=2$, then L is centrally nilpotent of class 2 and the group Mult(L) is a semidirect product of the normal subgroup $V=Z \times Inn(L) \cong \mathbb R^5$ by a group $Q \cong \mathbb R$, where $\mathbb R^2 =Z \cong Z(L)$. V contains the commutator subgroup $Mult(L)'$ of Mult(L). The group Mult(L) is either nilpotent or its Lie algebra has a 5-dimensional abelian nilradical. For every 1-dimensional connected subgroup I of Z the orbit I(e) is a connected central subgroup of L isomorphic to $\mathbb R$ and the factor loop L/I(e) is isomorphic either to the group $\mathbb R^2$ or to an elementary filiform loop $L_{\mathcal F}$. If $L/I(e) \cong \mathbb R^2$, then case d) (i) holds. If $L/I(e) \cong L_{\mathcal F}$, then the group Mult(L) has a normal subgroup S containing $I \cong \mathbb R$ such that one has $S(e)=I(e)$ and the factor group Mult(L)/S is isomorphic either to ${\mathcal F}_{4}$ or to ${\mathcal F}_{5}$. The case $Mult(L)/S \cong {\mathcal F}_{5}$ occurs only if $Mult(L)=\mathbb R \times {\mathcal F}_{5}$.

• f) If the group Mult(L) is nilpotent, then L is centrally nilpotent.

The next lemma, which is proved in [10], Proposition 3.3, is a useful tool to exclude those Lie algebras which are not the Lie algebra of the multiplication group of a 3-dimensional topological loop.

Lemma 4

Let L be a 3-dimensional proper connected simply connected topological loop having a 6-dimensional solvable Lie algebra $\mathbf{g}$ as the Lie algebra of its multiplication group.

• a) For each 1-dimensional ideal $\mathbf{i}$ of $\mathbf{g}$ the orbit I(e), where I is the simply connected Lie group of $\mathbf{i}$, is a normal subgroup of L isomorphic to $\mathbb R$. We have one of the following possibilities:

  • (i) The factor loop L/I(e) is isomorphic to $\mathbb R^2$. Then $\mathbf{g}$ contains the ideal $\mathbf{p}=\mathbf{z} \oplus \mathbf{inn(L)} \cong \mathbb R^4$ such that the commutator ideal $\mathbf{g}'$ of $\mathbf{g}$ lies in $\mathbf{p}$. Here $\mathbf{z}$ is the 1-dimensional centre of $\mathbf{g}$ and $\mathbf{inn(L)}$ is the Lie algebra of the inner mapping group Inn(L).

  • (ii) The factor loop L/I(e) is isomorphic either to the group ${\mathcal L}_2$ or to a loop $L_{\mathcal F}$. Then there exists an ideal $\mathbf{s}$ of $\mathbf{g}$ such that $\mathbf{i} \le \mathbf{s}$ and the factor Lie algebra $\mathbf{g}/\mathbf{s}$ is isomorphic either to $\mathbf{l}_2 \oplus \mathbf{l}_2$, where $\mathbf{l}_2$ is the 2-dimensional solvable non-abelian Lie algebra, or to an elementary filiform Lie algebra $\mathbf{f}_n$, $n=4, 5$.

• b) Let $\mathbf{a}$ be an ideal of $\mathbf{g}$ such that $\hbox {dim}(\mathbf{a})=2$, $\mathbf{a} \subseteq \mathbf{g}'$ and the factor Lie algebra $\mathbf{g}/\mathbf{a}$ is isomorphic neither to $\mathbf{l}_2 \oplus \mathbf{l}_2$ nor to $\mathbf{f}_4$. Then the orbit A(e), where A is the simply connected Lie group of $\mathbf{a}$, is either a 2-dimensional connected normal subloop M of L or the factor loop L/A(e) is isomorphic to $\mathbb R^2$.

If $A(e)=M$, then there exists a 5-dimensional ideal $\mathbf{v}$ of $\mathbf{g}$ containing the Lie algebra $\mathbf{inn(L)}$, the Lie algebra $\mathbf{mult}(M)$ of the multiplication group of M and the commutator ideal $\mathbf{g}'$ of $\mathbf{g}$. Let $\mathbf{b}$ be an ideal of $\mathbf{g}$ such that $\hbox {dim}(\mathbf{b}) \ge 3$, $\mathbf{a} \subset \mathbf{b} \subseteq \mathbf{g}'$. Then the orbit B(e), where B is the simply connected Lie group of $\mathbf{b}$, coincides with M. One has $\mathbf{a} \cap \mathbf{inn(L)}=\{ 0 \}$ and the intersection $\mathbf{b} \cap \mathbf{inn(L)}$ has dimension $\hbox {dim}(\mathbf{b})-2$.

If the factor loop L/A(e) is isomorphic to $\mathbb R^2$, then we have case (i).

3 The Case dim(Z)=0

This section is devoted to prove the following:

Proposition 2

The 6-dimensional decomposable solvable Lie algebras with trivial centre are not the Lie algebra of the multiplication group of a connected topological loop L of dimension 3.

Proof

We may assume that the loop L is simply connected and hence it is homeomorphic to $\mathbb R^{3}$ (cf. Lemma 2). Since the Lie algebra $\mathbf{mult(L)}$ of the group Mult(L) of L is a 6-dimensional decomposable solvable Lie algebra with trivial centre, for $\mathbf{mult(L)}$ we have the following possibilities: $\mathbf{l}_2 \oplus \mathbf{l}_2 \oplus \mathbf{l}_2$, $\mathbf{g}_{3,i} \oplus \mathbf{g}_{3,j}$, $\mathbf{l}_2 \oplus \mathbf{g}_{4,k}$, where $\mathbf{g}_{3,i}$, $\mathbf{g}_{3,j}$, $i,j \in \{2,3,4,5\}$, are the 3-dimensional solvable Lie algebras with trivial centre (cf. §4 in [14], p. 119), $\mathbf{g}_{4,k}$, $k=2,4,5,6,7,10$, $\mathbf{g}_{4,8}^{h \ne -1}$, $\mathbf{g}_{4,9}^{p \ne 0}$ are the 4-dimensional solvable Lie algebras with trivial centre (see §5 in [14], pp. 120-121). These Lie algebras have trivial centre and neither a subalgebra nor a factor Lie algebra is isomorphic to an elementary filiform Lie algebra $\mathbf{f}_n$, $n=4, 5$.

The Lie algebras $\mathbf{mult(L)}= \mathbf{l}_2 \oplus \mathbf{g}_{4,k}$, $k=2,4,5,6,7,10$, $\mathbf{l}_2 \oplus \mathbf{g}_{4,8}^{h \ne -1}$, $\mathbf{l}_2 \oplus \mathbf{g}_{4,9}^{p \ne 0}$, where $\mathbf{l}_2=\langle f_1,f_2 \rangle$, have the 1-dimensional ideal $\mathbf{i}=\langle f_1 \rangle$. There does not exist any ideal $\mathbf{s}$ of $\mathbf{mult(L)}$ such that $\mathbf{i} \subseteq \mathbf{s}$ and $\mathbf{mult(L)}/\mathbf{s}$ is isomorphic to the Lie algebra $\mathbf{l}_2 \oplus \mathbf{l}_2$. By Lemma 3 c) these Lie algebras are not the Lie algebra of the multiplication group of a loop L.

Now we treat the Lie algebras $\mathbf{g}_{i,j}=\mathbf{g}_{3,i} \oplus \mathbf{g}_{3,j}=\langle e_1, e_2, e_3 \rangle \oplus \langle e_4, e_5, e_6 \rangle$, $i,j \in \{2,3,4,5\}$. Let be $j=5$. The Lie algebra $\mathbf{g}_{3,5}$, respectively $\mathbf{g}_{4,5}$ is defined by $[e_1,e_3]=e_1$, $[e_2,e_3]=he_2$, $[e_4,e_6]=pe_4-e_5$, $[e_5,e_6]=e_4+pe_5$, $p \ge 0$, where $h=1$, respectively $-1 \le h <1$, whereas the Lie algebra $\mathbf{g}_{2,5}$ is given by $[e_1,e_3]=e_1$, $[e_2,e_3]=e_1+e_2$, $[e_4,e_6]=pe_4-e_5$, $[e_5,e_6]=e_4+pe_5$, $p \ge 0$. They have the 1-dimensional ideal $\mathbf{i}=\langle e_1 \rangle$. There does not exist any ideal $\mathbf{s}$ of $\mathbf{g}_{i,5}$, $i=2,3,4$, such that $\mathbf{i} \subseteq \mathbf{s}$ and $\mathbf{g}_{i,5}/\mathbf{s}$ is isomorphic to the Lie algebra $\mathbf{l}_2 \oplus \mathbf{l}_2$. The Lie algebra $\mathbf{g}_{5,5}$ defined by $[e_1,e_3]=p_1 e_1-e_2$, $[e_2,e_3]=e_1+p_1 e_2$, $[e_4,e_6]=p_2 e_4-e_5$, $[e_5,e_6]=e_4+p_2 e_5$ with $p_1,p_2\ge 0$ has the minimal ideals $\mathbf{s}_1=\langle e_1, e_2 \rangle$, $\mathbf{s}_2=\langle e_4, e_5 \rangle$. Let $S_i$, $i=1,2$, be the simply connected Lie groups of $\mathbf{s}_i$. If $\mathbf{g}_{5,5}$ were the Lie algebra of the multiplication group of L, then by Lemma 3 b) and c) at least one of the orbits $S_i(e)$, $i=1,2$, would be a normal subloop of L isomorphic to $\mathbb R$. For this orbit the factor loop $L/S_i(e)$ is isomorphic to the group ${\mathcal L}_2$. Since the factor Lie algebras $\mathbf{g}_{5,5}/\mathbf{s}_i$, $i=1,2$, are not isomorphic to the Lie algebra $\mathbf{l}_2 \oplus \mathbf{l}_2$ the Lie algebra $\mathbf{g}_{5,5}$ is excluded (cf. Lemma 4 (ii)).

The Lie algebras $\mathbf{g}_{3,3}$, $\mathbf{g}_{3,4}$, $\mathbf{g}_{4,4}$ are defined by $[e_1,e_3]=e_1$, $[e_2,e_3]=h_1 e_2$, $[e_4,e_6]=e_4$, $[e_5,e_6]=h_2 e_5$ such that for $\mathbf{g}_{3,3}$ one has $h_1=h_2=1$, for $\mathbf{g}_{3,4}$ one has $h_1=1$, $-1 \le h_2 <1$ and for $\mathbf{g}_{4,4}$ one has $-1 \le h_1,h_2 <1$. The Lie algebra $\mathbf{g}_{2,3}$, respectively $\mathbf{g}_{2,4}$ is given by $[e_1,e_3]=e_1$, $[e_2,e_3]=e_1+e_2$, $[e_4,e_6]=e_4$, $[e_5,e_6]=h_2 e_5$, where $h_2=1$, respectively $-1 \le h_2 <1$. The Lie algebra $\mathbf{g}_{2,2}$ is defined by $[e_1,e_3]=e_1$, $[e_2,e_3]=e_1+e_2$, $[e_4,e_6]=e_4$, $[e_5,e_6]=e_4+e_5$. All these Lie algebras have the ideals $\mathbf{i}_1=\langle e_1 \rangle$, $\mathbf{i}_2=\langle e_4 \rangle$. Additionally, the Lie algebra $\mathbf{g}_{3,3}$ has the ideals $\mathbf{i}_3=\langle e_2+ l_1 e_1 \rangle$, $\mathbf{i}_4=\langle e_5+ l_2 e_4 \rangle$, $l_1, l_2 \in \mathbb R$, the Lie algebra $\mathbf{g}_{4,4}$ has the ideals $\mathbf{i}_5=\langle e_2 \rangle$, $\mathbf{i}_6=\langle e_5 \rangle$, the Lie algebra $\mathbf{g}_{2,3}$ has the ideal $\mathbf{i}_4$, the Lie algebra $\mathbf{g}_{2,4}$ has the ideal $\mathbf{i}_6$, and the Lie algebra $\mathbf{g}_{3,4}$ has the ideals $\mathbf{i}_3$, $\mathbf{i}_6$. All Lie algebras have the ideal $\mathbf{s}_1=\langle e_1, e_4 \rangle$ containing $\mathbf{i}_1$, $\mathbf{i}_2$, such that the factor Lie algebras $\mathbf{g}_{i,j}/\mathbf{s}_1$, $i,j \in \{2,3,4\}$ are isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$. Furthermore, the Lie algebra $\mathbf{g}_{3,3}$ has the ideal $\mathbf{s}_2=\langle e_2+ l_1 e_1, e_5+ l_2 e_4 \rangle$, the Lie algebra $\mathbf{g}_{4,4}$ has the ideal $\mathbf{s}_3=\langle e_2, e_5 \rangle$, the Lie algebra $\mathbf{g}_{2,3}$ has the ideal $\mathbf{s}_4=\langle e_1, e_5+ l_2 e_4 \rangle$, the Lie algebra $\mathbf{g}_{2,4}$ has the ideal $\mathbf{s}_5=\langle e_1, e_5 \rangle$ and the Lie algebra $\mathbf{g}_{3,4}$ has the ideal $\mathbf{s}_6=\langle e_2+ l_1 e_1, e_5 \rangle$ such that the factor Lie algebras $\mathbf{g}_{3,3}/\mathbf{s}_2$, $\mathbf{g}_{4,4}/\mathbf{s}_3$, $\mathbf{g}_{2,3}/\mathbf{s}_4$, $\mathbf{g}_{2,4}/\mathbf{s}_5$, $\mathbf{g}_{3,4}/\mathbf{s}_6$ are isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$. If $\mathbf{g}_{i,j}$, $i,j \in \{2,3,4\}$, is the Lie algebra of the multiplication group of a 3-dimensional topological loop L, then the orbits $I_k(e)$, $k=1, \cdots ,6$, where $I_k=\exp (\mathbf{i}_k)$ and e is the identity element of L, are 1-dimensional normal subgroups of L isomorphic to $\mathbb R$ and the factor loops $L/I_k(e)$ are isomorphic to ${\mathcal L}_2$ (cf. Lemma 4 (ii)). All Lie algebras $\mathbf{g}_{i,j}$, $i,j \in \{2,3,4\}$, have the ideals $\mathbf{s}_7=\langle e_1, e_2 \rangle$, $\mathbf{s}_8=\langle e_4, e_5 \rangle$ such that the factor Lie algebras $\mathbf{g}_{i,j}/\mathbf{s}_l$, $l=7,8$, are not isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$. Hence the orbits $S_l(e)$, where $S_l = \exp (\mathbf{s}_l)$, $l=7,8$, and e is the identity element of L, are 2-dimensional normal subloops of L and therefore one has $\mathbf{s}_l \cap \mathbf{inn}(L) = \{ 0\}$, $l=7,8$ (cf. Lemma 4). All Lie algebras $\mathbf{g}_{i,j}$, $i,j \in \{2,3,4\}$, have the commutator subalgebra $\mathbf{n}_1=\langle e_1, e_2, e_4, e_5 \rangle$. Their 5-dimensional ideals are $\mathbf{v}_1=\langle e_1, e_2, e_4, e_5, e_3 \rangle$, $\mathbf{v}_{2,k}=\langle e_1, e_2, e_4, e_5, e_6+k e_3 \rangle$, $k \in \mathbb R$. Denote by $N_1$ the simply connected Lie group of $\mathbf{n}_1$. By Lemma 4 b) we have $N_1(e)=S_l(e)$, $l=7,8$. Therefore the intersection $\mathbf{n}_1 \cap \mathbf{inn}(L)$ has dimension 2. Hence the Lie algebra $\mathbf{inn}(L)$ has the basis elements $r_1=e_4+ a_1 e_1+ a_2 e_2$, $r_2=e_5+b_1 e_1+b_2 e_2$ such that at least one of $a_1, a_2$ as well as $b_1, b_2$ are different from 0 and $a_1 b_2-a_2 b_1 \ne 0$.

All Lie algebras $\mathbf{g}_{i,j}$, $i,j \in \{2,3,4\}$, have the ideals $\mathbf{n}_2=\langle e_1, e_2, e_3 \rangle$, $\mathbf{n}_3=\langle e_4, e_5, e_6 \rangle$. As $\mathbf{s}_7 < \mathbf{n}_2$ and $\mathbf{s}_8 < \mathbf{n}_3$ the orbits $N_j(e)$, where $N_j = \exp (\mathbf{n}_j)$, $j=2, 3$, have dimension 2 or 3. If $S_7(e)=N_2(e)$ or $S_8(e)=N_3(e)$, then one has $\hbox {dim}(\mathbf{n}_2 \cap \mathbf{inn}(L))=1$ or $\hbox {dim}(\mathbf{n}_3 \cap \mathbf{inn}(L))=1$. Hence the Lie algebra $\mathbf{inn}(L)$ has the basis element either $r_3=e_3+c_1 e_1+c_2 e_2$ or $r_3'=e_6+d_1 e_4+d_2 e_5$, $c_i, d_i \in \mathbb R$, $i=1,2$. Since $[r_1,r_3]$, respectively $[r_2,r_3']$ is a non-zero element of the ideal $\mathbf{s}_7$, respectively $\mathbf{s}_8$, the subspaces $\langle r_1, r_2, r_3 \rangle$, $\langle r_1, r_2, r_3' \rangle$ are not 3-dimensional subalgebras of $\mathbf{g}_{i,j}$, $i,j \in \{2,3,4\}$. This contradiction gives that $N_2(e)=L$ and $N_3(e)=L$. As $\mathbf{n}_2 < \mathbf{v}_1$ and $\mathbf{n}_3 < \mathbf{v}_{2,0}$ we obtain that $N_2(e)=V_1(e)=V_{2,0}(e)=N_3(e)=L$. By Lemma 3 c) there exists a parameter $k \in \mathbb R \setminus \{ 0 \}$ such that $V_{2,k}(e)$ is the 2-dimensional normal subloop $S_7(e)=S_8(e)$. Hence one has $\hbox {dim}(\mathbf{v}_{2,k} \cap \mathbf{inn}(L))=3$. Therefore the Lie algebra $\mathbf{inn}(L)$ has the basis element $r_4=e_6+ k e_3+l_1 e_1+l_2 e_2$ for some $k \in \mathbb R \setminus \{ 0 \}$, $l_i \in \mathbb R$, $i=1,2$.

The subspace $\langle r_1, r_2, r_4 \rangle$ is not a 3-dimensional subalgebra of the Lie algebras $\mathbf{g}_{2,3}$, $\mathbf{g}_{2,4}$, $\mathbf{g}_{3,4}$. Hence these Lie algebras cannot be the Lie algebra of the group Mult(L) of L.

The subspace $\langle r_1, r_2, r_4 \rangle$ forms a 3-dimensional subalgebra of $\mathbf{g}_{2,2}$ if and only if $k=1$, $a_2=0$ and $b_2=a_1 \ne 0$. Hence the subalgebra $\mathbf{inn}(L) < \mathbf{g}_{2,2}$ has the form $\mathbf{inn}(L)=\langle e_4+a_1 e_1, e_5+b_1 e_1+ a_1 e_2, e_6+e_3+l_1 e_1+ l_2 e_2 \rangle$, $a_1 \ne 0$, $b_1, l_i \in \mathbb R$.

The subspace $\langle r_1, r_2, r_4 \rangle$ forms a 3-dimensional subalgebra of $\mathbf{g}_{3,3}$ if and only if $k=1$. Hence the subalgebra $\mathbf{inn}(L) < \mathbf{g}_{3,3}$ has the form $\mathbf{inn}(L)=\langle e_4+a_1 e_1+ a_2 e_2, e_5+b_1 e_1+ b_2 e_2, e_6+e_3+l_1 e_1+ l_2 e_2 \rangle$ such that at least one of $a_1, a_2$ as well as $b_1, b_2$ are different from 0 and $a_1 b_2-a_2 b_1 \ne 0$.

The subspace $\langle r_1, r_2, r_4 \rangle$ forms a 3-dimensional subalgebra of $\mathbf{g}_{4,4}$ if and only if one has either $a_1=0=b_2$, $k=h_2=\frac{1}{h_1}$, or $a_2=0=b_1$, $k=1$, $h_2=h_1$. Therefore the subalgebra $\mathbf{inn}(L) < \mathbf{g}_{4,4}$ has either the form $\mathbf{inn}(L)=\langle e_4+a_2 e_2, e_5+b_1 e_1, e_6+k e_3+l_1 e_1+ l_2 e_2 \rangle$ such that $a_2 b_1 \ne 0$, $k=h_2=\frac{1}{h_1}$, or $\mathbf{inn}(L)=\langle e_4+a_1 e_1, e_5+b_2 e_2, e_6+e_3+l_1 e_1+ l_2 e_2 \rangle$ such that $a_1 b_2 \ne 0$, $h_1=h_2$.

Using the automorphism $\phi (e_1)=\frac{b_{2}e_{1}-a_{2}e_{2}}{a_{1}b_{2}-a_{2}b_{1}}$, $\phi (e_2)=\frac{b_{1}e_{1}-a_{1}e_{2}}{a_{2}b_{1}-a_{1}b_{2}}$, $\phi (e_3)=e_3-l_1 \phi (e_1)-l_2 \phi (e_2)$, $\phi (e_i)=e_i$, $i=4,5,6$, of the Lie algebras $\mathbf{g}_{i,i}$, $i=2,3,4$, such that for $\mathbf{g}_{2,2}$ one has $a_2=0, b_2=a_1\ne 0$ and for $\mathbf{g}_{4,4}$ we have $a_2=b_1=0$, $h_2=h_1$, we can reduce $\mathbf{inn}(L)$ to $\mathbf{inn}(L)_{1}=\langle e_4+e_1, e_5+e_2, e_6+e_3\rangle$. Moreover, the automorphism $\phi (e_1)=\frac{1}{b_1}e_1$, $\phi (e_2)=\frac{1}{a_2}e_2$, $\phi (e_3)=e_3-\frac{h_{1}l_{1}}{b_1}e_1-\frac{h_{1}l_{2}}{a_2}e_2$, $\phi (e_i)=e_i$, $i=4,5,6$, of the Lie algebra $\mathbf{g}_{4,4}$ with $h_2=\frac{1}{h_1}$ reduces $\mathbf{inn}(L)$ to $\mathbf{inn}(L)_{2}=\langle e_4+e_2, e_5+e_1, e_6+\frac{1}{h_1}e_3\rangle$. Linear representations of the simply connected Lie groups $G_{i,i}$, $i=2,3,4$, are given as follows: for $G_{2,2}$ one has

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad = g(x_1+(y_1+x_{3}y_{2})e^{x_3},x_2+y_2e^{x_3},x_3+y_3,x_4\\&\quad +(y_4+x_{6}y_{5})e^{x_6},x_5+y_5e^{x_6},x_6+y_6), \end{aligned}$$

for $G_{3,3}$, where $h_1=1$, and for $G_{4,4}$ with $h_2=h_1$ we have

$$\begin{aligned} g(x_1+y_1e^{x_3},x_2+y_2e^{h_{1}x_{3}},x_3+y_3,x_4+y_4e^{x_6},x_5+y_5e^{h_{1}x_{6}},x_6+y_6), \end{aligned}$$

for $G_{4,4}$, where $h_2=\frac{1}{h_1}$, one has

$$\begin{aligned} g(x_1+y_1e^{x_3},x_2+y_2e^{h_{1}x_3},x_3+y_3,x_4+y_4e^{x_6},x_5+y_5e^{\frac{x_6}{h_{1}}},x_6+y_6). \end{aligned}$$

We get that the subgroup $Inn(L)_{1}$ of $G_{2,2}$, $G_{3,3}$ and $G_{4,4}$ with $h_2=h_1$ has the form $Inn(L)_{1}=\{g(u_1,u_2,u_3,u_1,u_2,u_3); u_i \in \mathbb {R}\}$, $i=1,2,3$, and the subgroup $Inn(L)_{2}$ of $G_{4,4}$ with $h_2=\frac{1}{h_1}$ is $Inn(L)_{2}=\{g(u_2,u_1,\frac{1}{h_{1}}u_3,u_1,u_2,u_3); u_i \in \mathbb {R}\}$, $i=1,2,3$. Two arbitrary left transversals to the groups $Inn(L)_{1}$ and $Inn(L)_{2}$ in $G_{i,i}$, $i=2,3,4$, are

$$\begin{aligned}&A=\{g(u,v,w,f_1(u,v,w),f_2(u,v,w),f_3(u,v,w)): u,v,w \in \mathbb {R}\}, \\&B=\{g(k,l,m,g_1(k,l,m),g_2(k,l,m),g_3(k,l,m)): k,l,m \in \mathbb {R}\}, \end{aligned}$$

where $f_{i}(u,v,w):\mathbb {R}^{3}\rightarrow \mathbb {R}$ and $g_{i}(k,l,m):\mathbb {R}^{3}\rightarrow \mathbb {R}$, $i=1,2,3$, are continuous functions with $f_{i}(0,0,0)=g_{i}(0,0,0)=0$. For all $a\in A$, $b\in B$ the condition $a^{-1}b^{-1}ab\in Inn(L)_1$ holds if and only if in the cases $G_{2,2}$, $G_{3,3}$ with $h_1=1$ and $G_{4,4}$ with $h_2=h_1$ the equation

$$\begin{aligned}&le^{-h_{1}m}(1-e^{-h_{1}w})+ve^{-h_{1}w}(e^{-h_{1}m}-1) \nonumber \\&\quad = g_{2}(k,l,m)e^{-h_{1}g_3(k,l,m)}(1-e^{-h_{1}f_3(u,v,w)})\nonumber \\&\qquad + f_{2}(u,v,w)e^{-h_{1}f_3(u,v,w)}(e^{-h_{1}g_3(k,l,m)}-1), \end{aligned}$$

(1)

and additionally for $G_{2,2}$ the equation

$$\begin{aligned}&e^{-m}(1-e^{-w})(k-lm)+e^{-w}(e^{-m}-1)(u-vw)+(wl-mv)e^{-w-m} \nonumber \\&\quad = e^{-g_3(k,l,m)}(1-e^{-f_3(u,v,w)})(g_{1}(k,l,m)-g_{2}(k,l,m)g_{3}(k,l,m)) \nonumber \\&\qquad +e^{-f_3(u,v,w)}(e^{-g_3(k,l,m)}-1)(f_1(u,v,w)-f_{2}(u,v,w)f_{3}(u,v,w)) \nonumber \\&\qquad +(g_{2}(k,l,m)f_{3}(u,v,w)-f_{2}(u,v,w)g_{3}(k,l,m))e^{-f_3(u,v,w)-g_3(k,l,m)},\nonumber \\ \end{aligned}$$

(2)

for $G_{3,3}$ with $h_1=1$ and for $G_{4,4}$ with $h_2=h_1$ the equation

$$\begin{aligned}&ke^{-m}(1-e^{-w})+ue^{-w}(e^{-m}-1) \nonumber \\&\quad =g_1(k,l,m)e^{-g_3(k,l,m)}(1-e^{-f_3(u,v,w)})\nonumber \\&\quad +f_1(u,v,w)e^{-f_3(u,v,w)}(e^{-g_3(k,l,m)}-1) \end{aligned}$$

(3)

are satisfied for all $k,l,m,u,v,w \in \mathbb R$. The products $a^{-1}b^{-1}ab$ are contained in $Inn(L)_2$ if and only if the equations

$$\begin{aligned}&le^{-h_{1}m}(1-e^{-h_{1}w})+ve^{-h_{1}w}(e^{-h_{1}m}-1) \nonumber \\&\quad =g_1(k,l,m)e^{-g_3(k,l,m)}(1-e^{-f_3(u,v,w)})\nonumber \\&\qquad +f_1(u,v,w) e^{-f_3(u,v,w)}(e^{-g_3(k,l,m)}-1), \end{aligned}$$

(4)

$$\begin{aligned}&ke^{-m}(1-e^{-w})+ue^{-w}(e^{-m}-1)\nonumber \\&\quad =g_{2}(k,l,m)e^{-\frac{1}{h_{1}}g_3(k,l,m)}(1-e^{-\frac{1}{h_{1}}f_3(u,v,w)})\nonumber \\&\qquad +f_{2}(u,v,w)e^{-\frac{1}{h_{1}}f_3(u,v,w)}(e^{-\frac{1}{h_{1}}g_3(k,l,m)}-1) \end{aligned}$$

(5)

are satisfied for all $u,v,w,k,l,m\in \mathbb {R}$. Equation (1), respectively (4) is satisfied precisely if one has $f_3(u,v,w)=w$, $f_2(u,v,w)=v$, $g_3(k,l,m)=m$, $g_2(k,l,m)=l$, respectively $f_3(u,v,w)=h_{1}w$, $f_1(u,v,w)=v$, $g_3(k,l,m)=h_{1}m$, $g_1(k,l,m)=l$. Then $A\cup B$ does not generate the groups $G_{i,i}$, $i=2,3$, $G_{4,4}$ with $h_2=h_1$ and $G_{4,4}$ with $h_2=\frac{1}{h_1}$. By Proposition 1 the Lie algebras $\mathbf{g}_{i,i}$, $i=2,3$, $\mathbf{g}_{4,4}$ with $h_2=h_1$ and with $h_2=\frac{1}{h_1}$, are not the Lie algebras of the groups Mult(L) of 3-dimensional topological loops L.

Hence it remains to deal with the Lie algebra $\mathbf{g}=\mathbf{l}_2 \oplus \mathbf{l}_2 \oplus \mathbf{l}_2= \langle f_1,f_2 \rangle \oplus \langle f_3,f_4 \rangle \oplus \langle f_5,f_6 \rangle$ with the Lie brackets $[f_1,f_2]=f_1$, $[f_3,f_4]=f_3$, $[f_5,f_6]=f_5$. The Lie algebra $\mathbf{g}$ has the 1-dimensional ideals $\mathbf{i}_1=\langle f_1 \rangle$, $\mathbf{i}_2=\langle f_3 \rangle$, $\mathbf{i}_3=\langle f_5 \rangle$. The ideals $\mathbf{s}_1=\langle f_1,f_2 \rangle$, $\mathbf{s}_2=\langle f_3,f_4 \rangle$, $\mathbf{s}_3=\langle f_5,f_6 \rangle$ have the properties $\mathbf{i}_j \subset \mathbf{s}_j$ and $\mathbf{g}/\mathbf{s}_j$, $j=1,2,3$, are isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$. If $\mathbf{g}$ is the Lie algebra of the multiplication group of L, then the orbits $I_j(e)$, $j=1,2,3$, where $I_j$ is the simply connected Lie group of $\mathbf{i}_j$ and e is the identity element of L, are 1-dimensional normal subloops of L such that the factor loops $L/I_j(e)$ are isomorphic to the 2-dimensional non-abelian Lie group $\mathcal {L}_2$ (cf. Lemma 4 a) (ii)).

For the ideals $\mathbf{a}_1=\langle f_1,f_3 \rangle$, $\mathbf{a}_2=\langle f_1,f_5 \rangle$, $\mathbf{a}_3=\langle f_3,f_5 \rangle$ the factor Lie algebras $\mathbf{g}/\mathbf{a}_j$, $j=1,2,3$, are not isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$. Hence these ideals and the commutator ideal $\mathbf{g}'=\langle f_1, f_3, f_5 \rangle$ satisfy the condition of Lemma 4 b). Therefore the orbits $A_j(e)$ and $G'(e)$, where $A_j$, respectively $G'$ is the simply connected Lie group of $\mathbf{a}_j$, $j=1,2,3$, respectively $\mathbf{g}'$, are the same 2-dimensional normal subloop M of L. Furthermore, one has $\mathbf{inn(L)} \cap \mathbf{a}_j=\{0\}$ for all $j=1,2,3$ and $\hbox {dim}(\mathbf{g}' \cap \mathbf{inn(L)})=1$. The commutator subalgebra $\mathbf{inn(L)}'$ of $\mathbf{inn(L)}$ is the intersection $\mathbf{g}' \cap \mathbf{inn(L)}$. As every element of $\mathbf{inn(L)}'$ is contained in one of the ideals $\mathbf{a}_j$ and $\mathbf{inn(L)} \cap \mathbf{a}_j=\{0\}$ for all $j=1,2,3$, the Lie algebra $\mathbf{inn(L)}$ is abelian. The 5-dimensional ideals of $\mathbf{g}$ are:

$$\begin{aligned}&\mathbf{v}_1=\langle f_1, f_3, f_5, f_2+k_1 f_6, f_4+k_2 f_6 \rangle , \ \ \mathbf{v}_2=\langle f_1, f_3, f_5, f_2+k_3 f_4, f_6+k_4 f_4 \rangle , \\&\mathbf{v}_3=\langle f_1, f_3, f_5, f_4+k_5 f_2, f_6+k_6 f_2 \rangle , \ \ k_i \in \mathbb R, \ i=1, \dots , 6. \end{aligned}$$

Each 3-dimensional abelian subalgebra of a 5-dimensional ideal $\mathbf{v}_j$, $j=1,2,3$, contains a non-trivial ideal of $\mathbf{g}$. Hence the Lie algebra $\mathbf{g}=\mathbf{l}_2 \oplus \mathbf{l}_2 \oplus \mathbf{l}_2$ is not the Lie algebra of the multiplication group of a 3-dimensional topological loop. $\square$

Corollary 1

There does not exist any connected topological proper loop L of dimension $\le 3$ having a solvable Lie group of dimension $\le 6$ with discrete centre as the multiplication group of L.

Proof

A nilpotent multiplication Lie group has always non-discrete centre (cf. [5], Theorem 1 and [8], Theorem). Let $\hbox {dim}(L)=3$. If the multiplication group of L is solvable and has dimension $\le 5$, then it is decomposable having 1- or 2-dimensional centre (see Propositions 12, 13, 14, 15, 17 in [7]). For 6-dimensional solvable Lie groups the assertion follows from Theorems 3.6, 3.7 in [8], Proposition 13 in [11] and Proposition 2. $\square$

4 The Case dim(Z)=1

In this section we determine the 6-dimensional decomposable solvable Lie groups with 1-dimensional centre which are the multiplication group Mult(L) of a 3-dimensional connected simply connected topological loop L. These loops have a centre $Z(L) \cong \mathbb R$ such that the factor loop L/Z(L) is isomorphic to $\mathbb R^2$.

Proposition 3

Let L be a connected topological loop of dimension 3 such that its multiplication group Mult(L) is a 6-dimensional decomposable solvable Lie group with 1-dimensional centre. Then L has nilpotency class 2. Moreover, the following Lie algebra pairs can occur as the Lie algebra $\mathbf{g}$ of the group Mult(L) and the subalgebra $\mathbf{k}$ of the subgroup Inn(L):

If $\mathbf{g}$ has the form $\mathbf{g}=\mathbb {R}\oplus \mathbf{h}=\langle f_1\rangle \oplus \langle e_1,e_2,e_3,e_4,e_5\rangle$, where $\mathbf{h}$ is a 5-dimensional solvable indecomposable Lie algebra with trivial centre, then:

• $\mathbf{g}_1=\mathbb {R}\oplus \mathbf{g}_{5,19}^{\alpha =0,\beta \ne 0}$: $[e_2,e_3]=e_1$, $[e_1,e_5]=e_1$, $[e_2,e_5]=e_2$, $[e_4,e_5]=\beta e_4$, $\mathbf{k}_{1,\epsilon }=\langle e_1+f_1, e_2+\epsilon f_1, e_4+f_1 \rangle$, $\epsilon =0,1$,

• $\mathbf{g}_2=\mathbb {R}\oplus \mathbf{g}_{5,20}^{\alpha =0}$: $[e_2,e_3]=e_1$, $[e_1,e_5]=e_1$, $[e_2,e_5]=e_2$, $[e_4,e_5]=e_1+e_4$, $\mathbf{k}_{2,\epsilon }=\langle e_1+f_1, e_2+\epsilon f_1, e_4+a_3 f_1\rangle$, $a_3\in \mathbb {R}$, $\epsilon =0,1$,

• $\mathbf{g}_3=\mathbb {R}\oplus \mathbf{g}_{5,27}$: $[e_2,e_3]=e_1$, $[e_1,e_5]=e_1$, $[e_3,e_5]=e_3+e_4$, $[e_4,e_5]=e_1+e_4$, $\mathbf{k}_{3}=\langle e_1+f_1, e_3, e_4+a_3f_1\rangle$, $a_3\in \mathbb {R}$,

• $\mathbf{g}_4=\mathbb {R}\oplus \mathbf{g}_{5,28}^{\alpha =0}$: $[e_2,e_3]=e_1$, $[e_1,e_5]=e_1$, $[e_3,e_5]=e_3+e_4$, $[e_4,e_5]=e_4$, $\mathbf{k}_{4}=\langle e_1+a_1f_1, e_3, e_4+f_1\rangle$, $a_1\in \mathbb {R}\backslash \{0\}$,

• $\mathbf{g}_5=\mathbb {R}\oplus \mathbf{g}_{5,32}$: $[e_2,e_4]=e_1$, $[e_3,e_4]=e_2$, $[e_1,e_5]=e_1$, $[e_2,e_5]=e_2$, $[e_3,e_5]=he_1+e_3$, $\mathbf{k}_{5}=\langle e_1+f_1, e_2+a_2 f_1, e_3\rangle$, $h, a_2\in \mathbb {R}$,

• $\mathbf{g}_6=\mathbb {R}\oplus \mathbf{g}_{5,33}$: $[e_1,e_4]=e_1$, $[e_3,e_4]=\beta e_3$, $[e_2,e_5]=e_2$, $[e_3,e_5]=\gamma e_3$, $\beta ^{2}+\gamma ^{2}\ne 0$, $\mathbf{k}_{6}=\langle e_1+f_1, e_2+f_1, e_3+f_1\rangle$,

• $\mathbf{g}_7=\mathbb {R}\oplus \mathbf{g}_{5,34}$: $[e_1,e_4]=\alpha e_1$, $[e_2,e_4]=e_2$, $[e_3,e_4]=e_3$, $[e_1,e_5]=e_1$, $[e_3,e_5]=e_2$, $\mathbf{k}_{7}=\langle e_1+f_1, e_2+f_1, e_3+a_3f_1\rangle$, $\alpha , a_3\in \mathbb {R}$,

• $\mathbf{g}_8=\mathbb {R}\oplus \mathbf{g}_{5,35}$: $[e_1,e_4]=he_1$, $[e_2,e_4]=e_2$, $[e_3,e_4]=e_3$, $[e_1,e_5]=\alpha e_1$, $[e_2,e_5]=-e_3$, $[e_3,e_5]=e_2$, $h^{2}+\alpha ^{2}\ne 0$, $\mathbf{k}_{8,1}=\langle e_1+f_1, e_2+f_1, e_3+a_3f_1\rangle$, $a_3\in \mathbb {R}$, $\mathbf{k}_{8,2}=\langle e_1+f_1, e_2, e_3+f_1\rangle$.

If $\mathbf{g}$ is the Lie algebra $\mathbf{l}_2 \oplus \mathbf{n}=\langle f_1,f_2 \rangle \oplus \langle e_1,e_2,e_3,e_4 \rangle$, where $\mathbf{n}$ is a 4-dimensional solvable Lie algebra with 1-dimensional centre $\langle e_1 \rangle$, then:

• $\mathbf{g}_9=\mathbf{l}_{2}\oplus \mathbf{g}_{4,1}$: $[f_1,f_2]=f_1$, $[e_2,e_4]=e_1$, $[e_3,e_4]=e_2$, $\mathbf{k}_{9}=\langle f_1+e_1, e_2+a_2e_1, e_3\rangle$, $a_2\in \mathbb {R}$,

• $\mathbf{g}_{10}=\mathbf{l}_{2}\oplus \mathbf{g}_{4,3}$: $[f_1,f_2]=f_1$, $[e_1,e_4]=e_1$, $[e_3,e_4]=e_2$, $\mathbf{k}_{10}=\langle f_1+e_2, e_1+e_2, e_3\rangle$.

If $\mathbf{g}$ is either the Lie algebras $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$ or $\mathbf{l}_2\oplus \mathbb {R}\oplus \mathbf{g}_{3,i}$, $i=2,3,4,5$, where $\mathbf{g}_{3,1}=\langle e_1,e_2,e_3\rangle$ is the 3-dimensional nilpotent Lie algebra having the centre $\langle e_1\rangle$ and $\mathbf{g}_{3,i}=\langle e_4,e_5,e_6\rangle$ is a 3-dimensional solvable Lie algebra with trivial centre, then:

• $\mathbf{g}_{11}=\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,2}$: $[e_2,e_3]=e_1$, $[e_4,e_6]=e_4$, $[e_5,e_6]=e_4+e_5$, $\mathbf{k}_{11,1}=\langle e_2, e_4+e_1, e_5\rangle$, $\mathbf{k}_{11,2}=\langle e_3, e_4+e_1, e_5\rangle$,

• $\mathbf{g}_{12}=\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,3}$: $[e_2,e_3]=e_1$, $[e_4,e_6]=e_4$, $[e_5,e_6]=e_5$, $\mathbf{k}_{12,1}=\langle e_2, e_4+e_1, e_5+e_1\rangle$, $\mathbf{k}_{12,2}=\langle e_3, e_4+e_1, e_5+e_1 \rangle$,

• $\mathbf{g}_{13}=\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,4}$: $[e_2,e_3]=e_1$, $[e_4,e_6]=e_4$, $[e_5,e_6]=he_5$, $-1\le h< 1$, $h\ne 0$, $\mathbf{k}_{13,1}=\langle e_2, e_4+e_1, e_5+e_1\rangle$, $\mathbf{k}_{13,2}=\langle e_3, e_4+e_1, e_5+e_1\rangle$,

• $\mathbf{g}_{14}=\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,5}$: $[e_2,e_3]=e_1$, $[e_4,e_6]=pe_4-e_5$, $[e_5,e_6]=e_4+pe_5$, $p\ge 0$, $\mathbf{k}_{14,1}=\langle e_2, e_4+e_1, e_5+a_3e_1 \rangle$, $\mathbf{k}_{14,2}=\langle e_3, e_4+e_1, e_5+a_3e_1 \rangle$, $a_3\in \mathbb {R}\backslash \{0\}$, $\mathbf{k}_{14,3}=\langle e_2, e_4, e_5+e_1 \rangle$, $\mathbf{k}_{14,4}=\langle e_3, e_4, e_5+e_1\rangle$,

• $\mathbf{g}_{15}=\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,2}$: $[f_1,f_2]=f_1$, $[e_4,e_6]=e_4$, $[e_5,e_6]=e_4+e_5$, $\mathbf{k}_{15}=\langle f_1+e_3, e_4+e_3, e_5\rangle$,

• $\mathbf{g}_{16}=\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,3}$: $[f_1,f_2]=f_1$, $[e_4,e_6]=e_4$, $[e_5,e_6]=e_5$, $\mathbf{k}_{16}=\langle f_1+e_3, e_4+e_3, e_5+e_3\rangle$,

• $\mathbf{g}_{17}=\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,4}$: $[f_1,f_2]=f_1$, $[e_4,e_6]=e_4$, $[e_5,e_6]=he_5$, $-1\le h < 1$, $h\ne 0$, $\mathbf{k}_{17}=\langle f_1+e_3, e_4+e_3, e_5+e_3\rangle$,

• $\mathbf{g}_{18}=\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,5}$: $[f_1,f_2]=f_1$, $[e_4,e_6]=pe_4-e_5$, $[e_5,e_6]=e_4+pe_5$, $p\ge 0$, $\mathbf{k}_{18,1}=\langle f_1+e_3, e_4+e_3, e_5+a_3 e_3\rangle$, $a_3\in \mathbb {R}$, $\mathbf{k}_{18,2}=\langle f_1+e_3, e_4, e_5+e_3\rangle$.

Proof

By Lemma 2 we may assume that the loop L is simply connected and hence it is homeomorphic to $\mathbb R^{3}$. Every 6-dimensional decomposable solvable Lie algebra with 1-dimensional centre has one of the following forms: $\mathbb {R}\oplus \mathbf{h}$, $\mathbf{l}_{2}\oplus \mathbf{n}$, $\mathbf{g}_{3,1} \oplus \mathbf{g}_{3,i}$, and $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,i}$, where $\mathbf{h}$, $\mathbf{n}$, $\mathbf{g}_{3,i}$ are described in the assertion. For $\mathbf{h}$ we have the possibilities: $\mathbf{g}_{5,i}$, $i=7,9,11,12,13,16,17,18,21,23,24$, 27, 31, 32, 33, 34, 35, 36, 37 and $\mathbf{g}_{5,15}^{\gamma \ne 0}$, $\mathbf{g}_{5,j}^{\alpha =0}$, $j=19,20,28$, $\mathbf{g}_{5,k}^{p \ne 0}$, $k=25,26$, $\mathbf{g}_{5,30}^{h \ne -2}$. For $\mathbf{n}$ one has the following Lie algebras $\mathbf{g}_{4,i}$, $i=1,3$, $\mathbf{g}_{4,8}^{h=-1}$, $\mathbf{g}_{4,9}^{p=0}$ and for the 3-dimensional solvable Lie algebras with trivial centre we have $\mathbf{g}_{3,i}$, $i=2,3,4,5$ (cf. [14], §4, §5, and [15], §10, p. 105-106).

To prove the first assertion we have to show that L has a normal subloop N isomorphic to $\mathbb R$ such that the factor loop L/N is isomorphic to $\mathbb R^2$ (cf. Lemma 3 b) and d)). Assume first that the Lie algebra of the multiplication group of L has the form $\mathbb {R}\oplus \mathbf{h}=\langle f_1 \rangle \oplus \langle e_1,e_2,e_3,e_4,e_5 \rangle$. If $\mathbf{h}\ne \mathbf{g}_{5,i}$, $i=33,34$, then there does not exist any ideal $\mathbf{s}$ containing the centre $\mathbf{z}=\langle f_1 \rangle$ such that the factor Lie algebras $(\mathbb {R}\oplus \mathbf{h})/\mathbf{s}$ are isomorphic to $\mathbf{f}_n$, $n=4,5$ or to $\mathbf{l}_{2}\oplus \mathbf{l}_{2}$. According to Lemma 4 a) the factor loop L/Z(e), where $Z=\exp (\mathbf{z})$, is isomorphic to $\mathbb R^2$ and the orbit Z(e) is the normal subloop N.

The Lie algebras $\mathbb {R}\oplus \mathbf{g}_{5,i}$, $i=33,34$, have no factor Lie algebras isomorphic to $\mathbf{f}_n$, $n=4,5$. The Lie algebra $\mathbb {R}\oplus \mathbf{g}_{5,34}$ has the 1-dimensional ideal $\mathbf{i}=\langle e_1\rangle$. None of the factor Lie algebras $\mathbb {R}\oplus \mathbf{g}_{5,34}/\mathbf{s}$, where $\mathbf{s}$ is any ideal containing $\mathbf{i}$, is isomorphic to $\mathbf{l}_{2}\oplus \mathbf{l}_{2}$. Therefore the orbit I(e), where I is the simply connected Lie group of $\mathbf{i}$, can be chosen as the normal subloop N.

The Lie algebra $\mathbb {R}\oplus \mathbf{g}_{5,33}$, $\beta ^2+\gamma ^2 \ne 0$, have the ideals $\mathbf{i}_1=\langle f_1 \rangle$, $\mathbf{i}_2=\langle e_1 \rangle$, $\mathbf{i}_3=\langle e_2 \rangle$, $\mathbf{i}_4=\langle e_3 \rangle$. If $\mathbb {R}\oplus \mathbf{g}_{5,33}$ is the Lie algebra of the multiplication group of L, then the orbits $I_j(e)$, $j \in \{1, 2, 3, 4\}$, are normal subgroups of L isomorphic to $\mathbb R$. The factor loops $L/I_j(e)$, $j \in \{1, 2, 3, 4\}$, are isomorphic either to ${\mathcal L}_2$ or to $\mathbb R^2$ (cf. Lemma 4 a). If all factor loops $L/I_j(e)$, $j \in \{1, 2, 3, 4\}$, are isomorphic to ${\mathcal L}_2$, then by Lemma 4 a) (ii) there are 2-dimensional ideals $\mathbf{s}_j$, $j \in \{1, 2, 3, 4\}$, such that $\mathbf{i}_j \subset \mathbf{s}_j$ and the factor Lie algebras $\mathbb {R}\oplus \mathbf{g}_{5,33}/\mathbf{s}_j$ are isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$. For the ideal $\mathbf{s}_1=\mathbf{s}_4=\langle f_1, e_3 \rangle$ one has $\mathbb {R}\oplus \mathbf{g}_{5,33}/\mathbf{s}_l \cong \mathbf{l}_2 \oplus \mathbf{l}_2$, $l=1,4$. The factor Lie algebra $\mathbb {R}\oplus \mathbf{g}_{5,33}/\langle f_1, e_1 \rangle$ is isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$ if and only if $\gamma =0$ and $\mathbb {R}\oplus \mathbf{g}_{5,33}/\langle f_1, e_2 \rangle$ is isomorphic to $\mathbf{l}_2 \oplus \mathbf{l}_2$ precisely if $\beta =0$. This contradiction to $\beta ^2+\gamma ^2 \ne 0$ yields that at least one of the factor loops $L/I_j(e)$, $j \in \{1, 2, 3, 4\}$, is isomorphic to $\mathbb R^2$. For such $j \in \{1, 2, 3, 4\}$ the orbit $I_j(e)$ is the requested normal subgroup N of L.

Hence L is centrally nilpotent of class 2. By Lemma 4 a) (i) the Lie algebra $\mathbb {R}\oplus \mathbf{h}$ has a 4-dimensional abelian ideal $\mathbf{p}=\mathbf{z}\oplus \mathbf{k}$, where $\mathbf{z}=\langle f_1\rangle$ and $\mathbf{k}$ is the Lie algebra of the group Inn(L) and $\mathbf{p}$ contains the commutator subalgebra of $\mathbb {R}\oplus \mathbf{h}$. According to 3. of Lemma 1 the subalgebra $\mathbf{k}$ does not contain any non-zero ideal of $\mathbf{g}$ and the normalizer $N_\mathbf{g}(\mathbf{k})$ of $\mathbf{k}$ in $\mathbf{g}$ is $\mathbf{p}$. The commutator subalgebra of $\mathbb {R}\oplus \mathbf{h}$ coincides with the commutator subalgebra $\mathbf{h}'$ of $\mathbf{h}$. The intersection of $\mathbf{z}$ and $\mathbf{h}'$ is trivial. Since $\mathbf{h}'\subset \mathbf{p}$ the Lie algebra $\mathbf{h}$ has a 3-dimensional abelian commutator subalgebra. Then for the triples $(\mathbf{g}, \mathbf{p}, \mathbf{k})$ we obtain:

(a) The Lie algebras $\mathbb {R}\oplus \mathbf{g}_{5,j}^{\alpha =0}$, $j=19,20$, have the ideal $\mathbf{p}=\langle f_1,e_1,e_2,e_4 \rangle$, the subalgebra $\mathbf{k}$ has the form: $\mathbf{k}_{a_1,a_2,a_3}=\langle e_1+a_1f_1, e_2+a_2f_1, e_4+a_3f_1\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that:

in the case $\mathbb {R}\oplus \mathbf{g}_{5,19}^{\alpha =0}$ one has $a_1 a_3\ne 0$ since $\langle e_1\rangle$ and $\langle e_4\rangle$ are ideals of $\mathbb {R}\oplus \mathbf{g}_{5,19}^{\alpha =0}$,

in the case $\mathbb {R}\oplus \mathbf{g}_{5,20}^{\alpha =0}$ we have $a_1\ne 0$ since $\langle e_1\rangle$ is an ideal of $\mathbb {R}\oplus \mathbf{g}_{5,20}^{\alpha =0}$.

Applying the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{1})=a_1e_{1}$, $\phi (e_{2})=e_{2}$, $\phi (e_{3})=a_1e_{3}$, $\phi (e_{4})=a_3e_{4}$, $\phi (e_{5})=e_{5}$ for the Lie algebra $\mathbb {R}\oplus \mathbf{g}_{5,19}^{\alpha =0}$ if $a_2=0$, respectively $\phi (e_{2})=a_2e_{2}$, $\phi (e_{3})=\frac{a_1}{a_2}e_{3}$ if $a_2\ne 0$ we can reduce $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{1,\epsilon }$, where $\epsilon$ is equal to 0, respectively to 1. Using the automorphism $\phi (f_{1})=\frac{1}{a_1}f_{1}$, $\phi (e_{i})=e_{i}$, $i=1,2,3,4,5$, for the Lie algebra $\mathbb {R}\oplus \mathbf{g}_{5,20}^{\alpha =0}$ if $a_2=0$, respectively $\phi (f_{1})=f_{1}$, $\phi (e_{j})=a_1e_{j}$, $j=1,4$, $\phi (e_{2})=a_2e_{2}$, $\phi (e_{3})=\frac{a_1}{a_2}e_{3}$, $\phi (e_{5})=e_{5}$ if $a_2\ne 0$ the Lie algebra $\mathbf{k}_{a_1,a_2,a_3}$ reduces to $\mathbf{k}_{2,\epsilon }$, where $\epsilon$ is equal to 0, respectively to 1.

(b) For the Lie algebras $\mathbb {R}\oplus \mathbf{g}_{5,27}$ and $\mathbb {R}\oplus \mathbf{g}_{5,28}^{\alpha =0}$ we have $\mathbf{p}=\langle f_1,e_1,e_3,e_4 \rangle$, the subalgebra $\mathbf{k}$ has the form: $\mathbf{k}_{a_1,a_2,a_3}=\langle e_1+a_1f_1, e_3+a_2f_1, e_4+a_3f_1\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that:

in the case $\mathbb {R}\oplus \mathbf{g}_{5,27}$ one has $a_1\ne 0$, since $\langle e_1\rangle$ is an ideal of $\mathbb {R}\oplus \mathbf{g}_{5,27}$,

in the case $\mathbb {R}\oplus \mathbf{g}_{5,28}^{\alpha =0}$ one has $a_1 a_3\ne 0$ since $\langle e_1\rangle$ and $\langle e_4\rangle$ are ideals of $\mathbb {R}\oplus \mathbf{g}_{5,28}^{\alpha =0}$. Using the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=a_1e_{i}$, $i=1,4$, $\phi (e_{j})=e_{j}$, $j=2,5$, $\phi (e_{3})=a_1e_{3}+a_2e_1$ for $\mathbb {R}\oplus \mathbf{g}_{5,27}$, respectively $\phi (e_{1})=a_1a_3e_{1}$, $\phi (e_{2})=a_1e_{2}$, $\phi (e_{3})=a_3e_{3}+a_2e_4$, $\phi (e_{4})=a_3e_{4}$ for $\mathbb {R}\oplus \mathbf{g}_{5,28}^{\alpha =0}$ we can reduce $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{3}$, respectively to $\mathbf{k}_{4}$ in the assertion.

(c) The Lie algebras $\mathbb {R}\oplus \mathbf{g}_{5,i}$, $i=32,33,34,35$, have $\mathbf{p}=\langle f_1,e_1,e_2,e_3 \rangle$ and the subalgebra $\mathbf{k}$ has the form: $\mathbf{k}_{a_1,a_2,a_3}=\langle e_1+a_1f_1, e_2+a_2f_1, e_3+a_3f_1\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that:

in the case $\mathbb {R}\oplus \mathbf{g}_{5,32}$ we have $a_1\ne 0$ since $\langle e_1\rangle$ is an ideal of $\mathbb {R}\oplus \mathbf{g}_{5,32}$,

in the case $\mathbb {R}\oplus \mathbf{g}_{5,33}$ we have $a_1a_2a_3\ne 0$ since $\langle e_1\rangle$, $\langle e_2\rangle$ and $\langle e_3\rangle$ are ideals of $\mathbb {R}\oplus \mathbf{g}_{5,33}$,

in the case $\mathbb {R}\oplus \mathbf{g}_{5,34}$ we have $a_1a_2\ne 0$ since $\langle e_1\rangle$, $\langle e_2\rangle$ are ideals of $\mathbb {R}\oplus \mathbf{g}_{5,34}$, in the case $\mathbb {R}\oplus \mathbf{g}_{5,35}$ we have $a_1\ne 0$ and at least one of $\{a_2,a_3\}$ is different from 0 since $\langle e_1\rangle$ and $\langle e_2, e_3\rangle$ are ideals of $\mathbb {R}\oplus \mathbf{g}_{5,35}$. The automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=a_1e_{i}$, $i=1,2$, $\phi (e_{3})=a_1e_{3}+a_3e_1$ and $\phi (e_{j})=e_{j}$, $j=4,5$ for $\mathbb {R}\oplus \mathbf{g}_{5,32}$, respectively $\phi (e_{2})=a_2e_{2}$, $\phi (e_{3})=a_3e_{3}$ for $\mathbb {R}\oplus \mathbf{g}_{5,33}$, respectively $\phi (e_{s})=a_2e_{s}$, $s=2,3$ for $\mathbb {R}\oplus \mathbf{g}_{5,34}$ reduces the Lie algebra $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{5}$, respectively to $\mathbf{k}_{6}$, respectively to $\mathbf{k}_{7}$ in the assertion. Applying the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{1})=a_1e_{1}$, $\phi (e_{i})=a_2e_{i}$, $i=2,3$ and $\phi (e_{j})=e_{j}$, $j=4,5$, for the Lie algebra $\mathbb {R}\oplus \mathbf{g}_{5,35}$ if $a_1 a_2\ne 0$, respectively $\phi (e_{s})=a_3e_{s}$, $s=2,3$ if $a_1 a_3\ne 0$ and $a_2=0$ we can reduce $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{8,1}$, respectively $\mathbf{k}_{a_1,0,a_3}$ to $\mathbf{k}_{8,2}$ in the assertion.

Secondly, assume that the Lie algebra of the multiplication group of L has the shape: $\mathbf{l}_{2}\oplus \mathbf{n}=\langle f_1,f_2 \rangle \oplus \langle e_1,e_2,e_3,e_4\rangle$ as in the assertion. If $\mathbf{n}\ne \mathbf{g}_{4,1}$, then there does not exist any ideal $\mathbf{s}$ containing the ideal $\mathbf{i}=\langle f_1 \rangle$ such that the factor Lie algebra $(\mathbf{l}_{2}\oplus \mathbf{n})/\mathbf{s}$ is isomorphic to $\mathbf{f}_n$, $n=4,5$ or to $\mathbf{l}_{2}\oplus \mathbf{l}_{2}$. The Lie algebra $\mathbf{l}_{2}\oplus \mathbf{g}_{4,1}$ has the centre $\mathbf{i}=\langle e_1\rangle$, but it has no factor Lie algebra isomorphic to $\mathbf{l}_{2}\oplus \mathbf{l}_{2}$. None of the factor Lie algebras $\mathbf{l}_{2}\oplus \mathbf{g}_{4,1}/\mathbf{s}$, where $\mathbf{s}$ is any ideal containing $\mathbf{i}$, is isomorphic to $\mathbf{f}_n$, $n=4,5$. Hence in both cases the orbit I(e), where I is the simply connected Lie group of $\mathbf{i}$, is a normal subgroup of L isomorphic to $\mathbb R$ with the property that the factor loop L/I(e) is isomorphic to $\mathbb R^2$ (cf. Lemma 4 a). According to Lemma 3 a) and d), in both cases the orbit I(e) coincides with the centre Z(L) of L and L has nilpotency class 2.

Moreover, the Lie algebra $\mathbf{l}_{2}\oplus \mathbf{n}$ has a 4-dimensional abelian ideal $\mathbf{p}=\mathbf{z}\oplus \mathbf{k}$, where $\mathbf{z}$ is the 1-dimensional centre of $\mathbf{l}_{2}\oplus \mathbf {n}$ and $\mathbf{k}$ is the Lie algebra of the group Inn(L) such that $\mathbf{p}$ contains the commutator subalgebra of $\mathbf{l}_{2}\oplus \mathbf{n}$. The commutator subalgebra of $\mathbf{l}_{2}\oplus \mathbf{g}_{4,i}$, $i=1,3,8,9$, is the direct sum $\langle f_1 \rangle \oplus \mathbf{g}_{4,i}'$ where $\mathbf{g}_{4,i}'$ is the commutator subalgebra of $\mathbf{g}_{4,i}$. Since the commutator subalgebras $\mathbf{g}_{4,j}'$, $j=8,9$, are not abelian, the Lie algebras $\mathbf{l}_{2}\oplus \mathbf{g}_{4,j}$, $j=8,9$, are excluded. Now we deal with the Lie algebras $\mathbf{l}_{2}\oplus \mathbf{g}_{4,k}$, $k=1,3$.

(d) The Lie algebra $\mathbf{l}_{2}\oplus \mathbf{g}_{4,1}$ has the centre $\mathbf{z}=\langle e_1 \rangle$ and $\mathbf{p}$ is the ideal $\langle f_1,e_1,e_2,e_3 \rangle$. The subalgebra $\mathbf{k}$ has the form: $\mathbf{k}_{a_1,a_2,a_3}=\langle f_1+a_1e_1, e_2+a_2e_1, e_3+a_3e_1\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that $a_1\ne 0$ since $\langle f_1\rangle$ is an ideal of $\mathbf{l}_{2}\oplus \mathbf{g}_{4,1}$. The centre of the Lie algebra $\mathbf{l}_{2}\oplus \mathbf{g}_{4,3}$ is $\mathbf{z}=\langle e_2 \rangle$ and the ideal $\mathbf{p}$ is again $\langle f_1,e_1,e_2,e_3 \rangle$. The subalgebra $\mathbf{k}$ has the form: $\mathbf{k}_{a_1,a_2,a_3}=\langle f_1+a_1e_2, e_1+a_2e_2, e_3+a_3e_2\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that $a_1\ne 0$ and $a_2\ne 0$ since $\langle f_1\rangle$ and $\langle e_1\rangle$ are ideals of $\mathbf{l}_{2}\oplus \mathbf{g}_{4,3}$. The automorphism $\phi (f_{1})=a_1f_{1}$, $\phi (f_{2})=f_{2}$, $\phi (e_{3})=e_{3}-a_3e_1$, $\phi (e_{i})=e_{i}$, $i=1,2,4$, of $\mathbf{l}_{2}\oplus \mathbf{g}_{4,1}$, respectively $\phi (e_{1})=a_2e_{1}$, $\phi (e_{3})=e_{3}-a_3e_2$ of $\mathbf{l}_{2}\oplus \mathbf{g}_{4,3}$ reduces the Lie algebra $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{9}$, respectively to $\mathbf{k}_{10}$ in the assertion.

Finally, for the Lie algebras $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}=\langle e_1,e_2,e_3\rangle \oplus \langle e_4,e_5,e_6 \rangle$, respectively $\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,i}=\langle f_1,f_2\rangle \oplus \langle e_3\rangle \oplus \langle e_4,e_5,e_6\rangle$, $i=2,3,4,5$, there does not exist any ideal $\mathbf{s}_1$, respectively $\mathbf{s}_2$ containing the ideal $\mathbf{i}_1=\langle e_1 \rangle$, respectively $\mathbf{i}_2=\langle f_1 \rangle$ such that the factor Lie algebras $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}/\mathbf{s}_1$, respectively, $\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,i}/\mathbf{s}_2$ are isomorphic to $\mathbf{f}_n$, $n=4,5$ or to $\mathbf{l}_{2}\oplus \mathbf{l}_{2}$. Hence if $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$ or $\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,i}$, $i=2,3,4,5$, is the Lie algebra of the multiplication group of L, then the orbits $I_i(e)$, $i=1,2$, are the centre of L such that the factor loop $L/I_i(e)$, $i=1,2$, are isomorphic to $\mathbb {R}^2$ (cf. Lemma 3 a), d)). Hence L is centrally nilpotent of class 2.

According to Lemma 4 a) (i) we have to find an ideal $\mathbf{p}=\mathbf{z}\oplus \mathbf {k} \cong \mathbb R^4$ of the Lie algebras $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$ and $\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,i}$, $i=2,3,4,5$, where $\mathbf{z}$ is their 1-dimensional centre, $\mathbf{p}$ contains their commutator subalgebra, and $\mathbf{k}$ is the Lie algebra of the group Inn(L) satisfying the assertion 3. of Lemma 1.

(e) The Lie algebras $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$, $i=2,3,4,5$, have the centre $\mathbf{z}=\langle e_1 \rangle$, and the ideal $\mathbf{p}$ has one of the forms : $\mathbf{p}_{r}=\langle e_1,e_2+re_3,e_4,e_5 \rangle$, $r\in \mathbb {R}$, and $\widetilde{\mathbf{p}}=\langle e_1,e_3,e_4,e_5 \rangle$. With respect to the ideals $\mathbf{p}_{r}$, $\widetilde{\mathbf{p}}$ we obtain the subalgebras $\mathbf{k}_{r}=\langle e_2+re_3+a_1e_1, e_4+a_2e_1, e_5+a_3e_1 \rangle$, $\mathbf{k}_{a_1,a_2,a_3}=\langle e_3+a_1e_1 ,e_4+a_2e_1, e_5+a_3e_1 \rangle$, $r,a_i\in \mathbb {R}$, $i=1,2,3$, such that: in the case $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,2}$ one has $a_2\ne 0$ since $\langle e_4\rangle$ is an ideal of $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,2}$, in the cases $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$, $i=3,4$, one has $a_2a_3\ne 0$ since $\langle e_4\rangle$, $\langle e_5\rangle$ are ideals of $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$, in the case $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,5}$ one has $a_2\ne 0$ or $a_3\ne 0$ since $\langle e_4, e_5\rangle$ is an ideal of $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,5}$. The automorphism $\phi (e_{2})=e_{2}-re_3-a_1e_1$, $\phi (e_{4})=a_2e_{4}$, $\phi (e_{5})=a_2e_{5}+a_3e_4$ and $\phi (e_{j})=e_{j}$, $j=1,3,6$, respectively $\phi (e_{2})=e_{2}$, $\phi (e_{3})=e_{3}-a_1e_1$ of $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,2}$ maps the subalgebra $\mathbf{k}_{r}$ onto $\mathbf{k}_{11,1}$, respectively $\mathbf{k}_{a_1,a_2,a_3}$ onto $\mathbf{k}_{11,2}$. The automorphism $\phi (e_{2})=e_{2}-re_3-a_1e_1$, $\phi (e_{4})=a_2e_{4}$, $\phi (e_{5})=a_3e_5$ and $\phi (e_{j})=e_{j}$, $j=1,3,6$, respectively $\phi (e_{2})=e_{2}$ and $\phi (e_{3})=e_{3}-a_1e_1$ of $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,i}$, $i=3,4$, maps the subalgebra $\mathbf{k}_{r}$ onto $\mathbf{k}_{12,1}=\mathbf{k}_{13,1}$, respectively $\mathbf{k}_{a_1,a_2,a_3}$ onto $\mathbf{k}_{12,2}=\mathbf{k}_{13,2}$ in the assertion. For the Lie algebra $\mathbf{g}_{3,1}\oplus \mathbf{g}_{3,5}$ the automorphism $\phi (e_{2})=e_2-re_3-a_1e_{1}$, $\phi (e_{j})=a_2e_{j}$, $j=4,5$, $\phi (e_{i})=e_{i}$, $i=1,3,6$, respectively $\phi (e_{2})=e_2$, $\phi (e_{3})=e_{3}-a_1e_1$ if $a_2\ne 0$ reduces $\mathbf{k}_{r}$ to $\mathbf{k}_{14,1}$, respectively $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{14,2}$. Moreover, if $a_3\ne 0$ and $a_2=0$, then the automorphism $\phi (e_{2})=e_2-re_3-a_1e_{1}$, $\phi (e_{j})=a_3e_{j}$, $j=4,5$, $\phi (e_{i})=e_{i}$, $i=1,3,6$, respectively $\phi (e_{2})=e_2$, $\phi (e_{3})=e_{3}-a_1e_1$, changes the Lie algebra $\mathbf{k}_{r}$ to $\mathbf{k}_{14,3}$, respectively $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{14,4}$ in the assertion.

The centre of the Lie algebras $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,i}$ with $i=2,3,4,5$, is $\mathbf{z}=\langle e_3\rangle$ and their ideal $\mathbf{p}$ is $\langle f_1,e_4,e_5,e_3\rangle$. The subalgebra $\mathbf{k}$ has the form: $\mathbf{k}_{a_1,a_2,a_3}=\langle f_1+a_1e_3, e_4+a_2e_3, e_5+a_3e_3\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that: in the case $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,2}$ one has $a_1 a_2\ne 0$ since $\langle f_1\rangle$ and $\langle e_4\rangle$ are ideals of $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,2}$, in the cases $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,i}$, $i=3,4$, one has $a_1a_2a_3\ne 0$ since $\langle f_1\rangle$, $\langle e_4\rangle$ and $\langle e_5\rangle$ are ideals of $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,i}$, in the case $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,5}$ one has $a_1\ne 0$ and at least one of $\{a_2, a_3\}$ is different from 0 since $\langle f_1\rangle$ and $\langle e_4, e_5\rangle$ are ideals of $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,5}$. Using the automorphism $\phi (f_{1})=a_1f_{1}$, $\phi (f_{2})=f_{2}$, $\phi (e_{4})=a_2e_{4}$, $\phi (e_{5})=a_{2}e_{5}+a_3e_4$ and $\phi (e_{j})=e_{j}$, $j=3,6$, for $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,2}$, respectively $\phi (e_{5})=a_{3}e_{5}$ for $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,i}$, $i=3,4$, the Lie algebra $\mathbf{k}_{a_1,a_2,a_3}$ reduces to $\mathbf{k}_{15}$, respectively to $\mathbf{k}_{16}=\mathbf{k}_{17}$. Applying the automorphism $\phi (f_{1})=a_1f_{1}$, $\phi (f_{2})=f_{2}$, $\phi (e_{4})=a_2e_{4}$, $\phi (e_{5})=a_{2}e_{5}$ and $\phi (e_{j})=e_{j}$, $j=3,6$, for $\mathbf{l}_{2}\oplus \mathbb {R} \oplus \mathbf{g}_{3,5}$ if $a_1 a_2\ne 0$, respectively $\phi (e_{4})=a_{3}e_{4}$ and $\phi (e_{5})=a_{3}e_{5}$ if $a_1 a_3\ne 0$ and $a_2=0$ we can reduce $\mathbf{k}_{a_1,a_2,a_3}$ to $\mathbf{k}_{18,1}$, respectively $\mathbf{k}_{a_1,0,a_3}$ to $\mathbf{k}_{18,2}$. $\square$

Using ([23], §4) we obtain:

Lemma 5

The simply connected Lie group $G_i$ and its subgroup $K_i$, with Lie algebra $\mathbf{g}_i$, and its subalgebra $\mathbf{k}_i$, $i=1,...,18$, are isomorphic to the linear groups the multiplication of which is given by:

for $i=1$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad =g( x_1+(y_1-x_3y_2)e^{x_5},x_2+y_2e^{x_5},(x_3+y_3)e^{x_5+y_5},x_4\\&\qquad +y_4e^{bx_5},x_5+y_5,x_6+y_6),\\&K_{1,\epsilon }=\{g(u_1,u_2,0,u_3,0,u_1\!+\!\epsilon u_2+u_3); u_i \!\in \! \mathbb R, i=1,2,3 \}, b\!\in \! \mathbb {R}\backslash \{0\}, \epsilon =0,1, \end{aligned}$$

for $i=2$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+(y_1-x_3y_2+x_5y_4)e^{x_5}, \\&x_2+y_2e^{x_5},(x_3+y_3)e^{x_5+y_5},x_4+y_4e^{x_5},x_5+y_5,x_6+y_6), \\&K_{2,\epsilon }=\{g(u_1,u_2,0,u_3,0,u_1\!+\!\epsilon u_2+a_3u_3); u_i \!\in \!\mathbb R, i=1,2,3 \}, \epsilon =0,1, a_3\!\in \!\mathbb R, \end{aligned}$$

for $i=3$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad =g(x_1+(y_1+x_5y_4+\frac{1}{2}(2x_2+x_5^{2})y_3)e^{x_5},(x_2+y_2+\frac{1}{2}(x_5+y_5)^{2})e^{x_5+y_5}, \\&x_3+y_3e^{x_5},x_4+(y_4+x_5y_3)e^{x_5},x_5+y_5,x_6+y_6), \\&K_{3}=\{g(u_1,0,u_2,u_3,0,u_1+a_3u_3); u_i \in \mathbb R, i=1,2,3 \}, a_3\in \mathbb R, \end{aligned}$$

for $i=4$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6)g(y_1,y_2,y_3,y_4,y_5,y_6)= g(x_1+(y_1+x_2y_3)e^{x_5}, \\&(x_2+y_2)e^{x_5+y_5},x_3+y_3e^{x_5},x_4+(y_4+x_5y_3)e^{x_5},x_5+y_5,x_6+y_6), \\&K_{4}=\{g(u_1,0,u_2,u_3,0,a_1u_1+u_3); u_i \in \mathbb R, i=1,2,3 \}, a_1\in \mathbb {R}\backslash \{0\}, \end{aligned}$$

for $i=5$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)\\&\quad = g(x_1+(y_1+x_4y_2+ax_5y_3+\frac{1}{2}x_4^{2}y_3)e^{x_5},x_2+(y_2+x_4y_3)e^{x_5}, \\&x_3+y_3e^{x_5},(x_4+y_4)e^{x_5+y_5},x_5+y_5,x_6+y_6), a\in \mathbb {R}, \\&K_{5}=\{g(u_1,u_2,u_3,0,0,u_1+a_2u_2);u_i \in \mathbb R, i=1,2,3 \}, a_2\in \mathbb R, \end{aligned}$$

for $i=6$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad =g(x_1+y_1e^{x_4},x_2+y_2e^{x_5},x_3+y_3e^{ax_5+bx_4},x_4+y_4,x_5+y_5,x_6+y_6), \\&K_{6}=\{g(u_1,u_2,u_3,0,0,u_1+u_2+u_3); u_i \in \mathbb R, i=1,2,3 \}, a^2+b^2\ne 0, \end{aligned}$$

for $i=7$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+y_1e^{ax_4+x_5}, \\&x_2+(y_2+x_5y_3)e^{x_4},x_3+y_3e^{x_4},x_4+y_4e^{ax_4+x_5},(x_5+y_5)e^{x_4+y_4},x_6+y_6), \\&K_{7}=\{g(u_1,u_2,u_3,0,0,u_1+u_2+a_3u_3);u_i \in \mathbb R, i=1,2,3 \}, a, a_3\in \mathbb R, \end{aligned}$$

for $i=8$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)= g(x_1+y_1e^{ax_5+bx_4}, \\&x_2+(y_2\cos (x_5)-y_3 \sin (x_5))e^{x_4},x_3+(y_3 \cos (x_5)+y_2 \sin (x_5))e^{x_4}, \\&x_4+y_4,x_5+y_5,x_6+y_6), a^2+b^2\ne 0,\\&K_{8,1}=\{g(u_1,u_2,u_3,0,0,u_1+u_2+a_3u_3);u_i \in \mathbb R, i=1,2,3 \}, a_3\in \mathbb R,\\&K_{8,2}=\{g(u_1,u_2,u_3,0,0,u_1+u_3); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=9$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&=g(x_1\!+\!y_1\!+\!x_4y_2\!+\!\frac{1}{2}x_4^{2}y_3,x_2\!+\!y_2\!+\!x_4y_3,x_3\!+\!y_3,x_4\!+\!y_4,x_5\!+\!y_5e^{x_6},x_6\!+\!y_6), \\&K_{9}=\{g(u_1+a_2u_2,u_2,u_3,0,u_1,0);u_i \in \mathbb R, i=1,2,3 \}, a_2\in \mathbb R, \end{aligned}$$

for $i=10$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad = g(x_1+y_1e^{x_4},x_2+y_2+x_4y_3,x_3+y_3,x_4+y_4,x_5+y_5e^{x_6},x_6+y_6), \\&K_{10}=\{g(u_1,u_1+u_3,u_2,0,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=11$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+y_1+x_2y_3, \\&x_2+y_2,x_3+y_3,x_4+(y_4+x_6y_5)e^{x_6},x_5+y_5e^{x_6},x_6+y_6), \\&K_{11,1}=\{g(u_2,u_1,0,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \\&K_{11,2}=\{g(u_2,0,u_1,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=12$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)\\ \\&\quad = g(x_1+y_1+x_2y_3,x_2+y_2,x_3+y_3,x_4+y_4e^{x_6},x_5+y_5e^{x_6},x_6+y_6), \\&K_{12,1}=\{g(u_2+u_3,u_1,0,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \\&K_{12,2}=\{g(u_2+u_3,0,u_1,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=13$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+y_1+x_2y_3, \\&x_2+y_2,x_3+y_3,x_4+y_4e^{x_6},x_5+y_5e^{hx_6},x_6+y_6), -1\le h<1, h\ne 0, \\&K_{13,1}=\{g(u_2+u_3,u_1,0,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \\&K_{13,2}=\{g(u_2+u_3,0,u_1,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=14$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)\!=\! g(x_1\!+\!y_1\!+\!x_2y_3,x_2\!+\!y_2,x_3\!+\!y_3,\\&x_4+(y_4 \cos (x_6)+y_5 \sin (x_6))e^{px_6},x_5+(y_5 \cos (x_6)-y_4 \sin (x_6))e^{px_6},x_6+y_6), \\&p\ge 0, K_{14,1}=\{g(u_2+a_3u_3,u_1,0,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3, \}, a_3\in \mathbb {R}\backslash \{0\}, \\&K_{14,2}=\{g(u_2+a_3u_3,0,u_1,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3, \}, a_3\in \mathbb {R}\backslash \{0\}, \\&K_{14,3}=\{g(u_3,u_1,0,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \\&K_{14,4}=\{g(u_3,0,u_1,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=15$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad =g(x_1+y_1e^{x_2},x_2\!+\!y_2,x_3\!+\!y_3e^{x_2},x_4\!+\!(y_4\!+\!x_6y_5)e^{x_6},x_5\!+\!y_5e^{x_6},x_6+y_6), \\&K_{15}=\{g(u_1,0,u_1+u_2,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=16$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad = g(x_1+y_1e^{x_2},x_2+y_2,x_3+y_3e^{x_2},x_4+y_4e^{x_6},x_5+y_5e^{x_6},x_6+y_6), \\&K_{16}=\{g(u_1,0,u_1+u_2+u_3,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=17$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+y_1e^{x_2}, \\&x_2+y_2,x_3+y_3e^{x_2},x_4+y_4e^{x_6},x_5+y_5e^{hx_6},x_6+y_6), -1\le h <1, h\ne 0, \\&K_{17}=\{g(u_1,0,u_1+u_2+u_3,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

for $i=18$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)\!=\! g(x_1\!+\!y_1e^{x_2},x_2\!+\!y_2,x_3\!+\!y_3e^{x_2}, \\&x_4+(y_4 \cos (x_6)+y_5 \sin (x_6))e^{px_6},x_5+(y_5 \cos (x_6)-y_4 \sin (x_6))e^{px_6},x_6+y_6), \\&p\ge 0, \ K_{18,1}=\{g(u_1,0,u_1+u_2+a_3u_3,u_2,u_3,0);u_i \in \mathbb R, i=1,2,3 \}, a_3\in \mathbb R,\\&K_{18,2}=\{g(u_1,0,u_1+u_3,u_2,u_3,0); u_i \in \mathbb R, i=1,2,3 \}. \end{aligned}$$

Proposition 4

There does not exist any 3-dimensional connected topological proper loop L such that the Lie algebra $\mathbf{g}$ of the multiplication group of L is one of the Lie algebras $\mathbf{g}_i$, $i=14,18$, with $p=0$.

Proof

We may assume that L is simply connected and hence it is homeomorphic to $\mathbb R^3$ (cf. Lemma 2). We show that none of the groups $G_i$, $i=14,18$, such that $p=0$ allows the existence of continuous left transversals A and B to $K_i$ in $G_i$ such that for all $a \in A$ and $b \in B$ one has $a^{-1} b^{-1} a b \in K_i$ and $A\cup B$ generates $G_i$. Hence Proposition 1 yields that the groups $G_i$, $i=14,18$, with $p=0$ are not the multiplication group of a loop L. This proves the assertion.

Two arbitrary left transversals to the groups $K_{14,i}$, $i=1,3$, in $G_{14}$ are:

$$\begin{aligned}&A =\{g(u, f_1(u,v,w),v,f_2(u,v,w) , f_3(u,v,w), w); u,v,w \in \mathbb R \}, \\&B =\{g(k, g_1(k,l,m), l, g_2(k,l,m), g_3(k,l,m), m); k,l,m \in \mathbb R \}, \end{aligned}$$

those to the groups $K_{14,j}$, $j=2,4$, in $G_{14}$ are:

$$\begin{aligned}&A =\{g(u,v,f_1(u,v,w),f_2(u,v,w) , f_3(u,v,w), w); u,v,w \in \mathbb R \}, \\&B =\{g(k,l,g_1(k,l,m), g_2(k,l,m), g_3(k,l,m), m); k,l,m \in \mathbb R \}, \end{aligned}$$

and those to the groups $K_{18,j}$, $j=1,2$, in $G_{18}$ are:

$$\begin{aligned}&A =\{g(f_1(u,v,w),u,v,f_2(u,v,w), f_3(u,v,w), w); u,v,w \in \mathbb R \}, \\&B =\{g(g_1(k,l,m),k, l, g_2(k,l,m), g_3(k,l,m), m); k,l,m \in \mathbb R \}, \end{aligned}$$

where $f_i(u,v,w): \mathbb R^3 \rightarrow \mathbb R$ and $g_i(k,l,m): \mathbb R^3 \rightarrow \mathbb R$, $i =1,2,3$, are continuous functions such that $f_i(0,0,0)= g_i(0,0,0)= 0$. The products $a^{-1}b^{-1}ab$, $a\in A$, $b \in B$ are elements in $K_{14,1}$, respectively in $K_{14,2}$, respectively in $K_{18,1}$ if and only if

$$\begin{aligned}&(\cos (m) -1)(f_2(u,v,w)(\cos (w) +a_3 \sin (w))\!+\!f_3(u,v,w)(a_3 \cos (w)\!-\! \sin (w)))\nonumber \\&+(\cos (w) \!-\!1)(g_3(k,l,m)(\sin (m) \!-\!a_3 \cos (m))\!-\!g_2(k,l,m)(\cos (m) \!+\!a_3 \sin (m))) \nonumber \\&-\sin (m)(f_2(u,v,w)(\sin (w)-a_3 \cos (w))+f_3(u,v,w)(\cos (w)+a_3 \sin (w))) \nonumber \\&+ \sin (w)(g_3(k,l,m)(\cos (m)+a_3 \sin (m))+g_2(k,l,m)(\sin (m)-a_3 \cos (m))) \nonumber \\&=f_1(u,v,w)l-g_1(k,l,m)v, \end{aligned}$$

(6)

respectively

$$\begin{aligned} g_1(k,l,m)v-f_1(u,v,w)l,\end{aligned}$$

(7)

respectively

$$\begin{aligned} e^{-u}(1-e^{-k})(f_1(u,v,w)-v)-e^{-k}(1-e^{-u})(g_1(k,l,m)-l) \end{aligned}$$

(8)

are satisfied for all $k,l,m,u,v,w\in \mathbb {R}$, with $a_3 \in \mathbb {R}$. Moreover, the products $a^{-1}b^{-1}ab$, $a\in A$, $b \in B$ are elements in $K_{14,3}$, respectively in $K_{14,4}$, respectively in $K_{18,2}$ precisely if

$$\begin{aligned}&(\cos (m)-1)(f_2(u,v,w) \sin (w)+f_3(u,v,w) \cos (w))\nonumber \\&\quad - (\cos (w)-1)(g_2(k,l,m) \sin (m)+g_3(k,l,m) \cos (m))\nonumber \\&\quad +\sin (m)(f_2(u,v,w) \cos (w)-f_3(u,v,w) \sin (w)) \nonumber \\&\quad + \sin (w)(g_3(k,l,m) \sin (m)-g_2(k,l,m) \cos (m))\nonumber \\&\quad = f_1(u,v,w)l-g_1(k,l,m)v, \end{aligned}$$

(9)

respectively

$$\begin{aligned} g_1(k,l,m)v-f_1(u,v,w)l,\end{aligned}$$

(10)

respectively

$$\begin{aligned} e^{-u}(1-e^{-k})(f_1(u,v,w)-v)-e^{-k}(1-e^{-u})(g_1(k,l,m)-l) \end{aligned}$$

(11)

hold for all $k,l,m,u,v,w \in \mathbb R$. The equations (6), (7), (8), (9), (10) and (11) are satisfied precisely if their left hand side as well as their right hand side are zero. The right hand side of these equations is zero if and only if $f_1(u,v,w)=v$ and $g_1(k,l,m)=l$. In that case the set $A\cup B$ does not generate $G_{14}$, respectively $G_{18}$. $\square$

Theorem 1

Let L be a 3-dimensional simply connected topological proper loop such that its multiplication group is a 6-dimensional solvable decomposable Lie group having 1-dimensional centre. Then the pairs of the Lie groups $(G_i,K_i)$, $i=1,\cdots ,18$, given in Lemma 5 such that for $i=14,18$ one has $p\ne 0$ are the multiplication group Mult(L) and the inner mapping group Inn(L) of L.

Proof

Taking into account Propositions 3 and 4 it remains to find for each group $G_i$, $i=1,\cdots ,18$, in Lemma 5, such that for $i=14,18$ one has $p\ne 0$, $K_i$-connected left transversals $A_i$, $B_i$ (cf. Proposition 1). The sets

$$\begin{aligned}&A_{1,0}=\{g(1-e^{v}-ue^{v}(1-e^{-bv}),e^{v}(1-e^{-bv}),u,ue^{bv-v},v,w); u, v, w \in \mathbb R\}, \\&B_{1,0}=\{g(1-e^{l}-ke^{l}(e^{-bl}-1),e^l(e^{-bl}-1),k,-ke^{bl-l},l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{1,1}\!=\!\{g(1\!-\!e^{v}(2\!+\!u\!-\!e^{-bv}\!-\!ue^{-bv}),e^{v}(1\!-\!e^{-bv}),u,ue^{bv-v},v,w); u, v, w \!\in \! \mathbb R\}, \\&B_{1,1}=\{g(1-e^{l}(e^{-bl}+ke^{-bl}-k),e^l(e^{-bl}-1),k,-ke^{bl-l},l,m); k, l, m \in \mathbb R \} \end{aligned}$$

are $K_{1,0}$-, respectively $K_{1,1}$-connected left transversals in $G_{1}^{b\ne 0}$. The sets

$$\begin{aligned} A_{2,0}=B_{2,0}=\{g(v^{2}-u^{2}-a_{3}v+e^{v}-1,u,u,v,v,w); u, v, w \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned} A_{2,1}=B_{2,1}=\{g(v^{2}-u^{2}-u-a_{3}v+e^{v}-1,u,u,v,v,w); u, v, w \in \mathbb R\},\end{aligned}$$

$a_3 \in \mathbb R$, are $K_{2,0}$-, respectively $K_{2,1}$-connected left transversals in $G_2$. The sets

$$\begin{aligned}&A_{3}=B_{3}=\{g(e^{v}-1+(v-a_3)v(1+u+a_3v-\frac{1}{2}v^{2})+(u+a_3v-\frac{1}{2}v^{2})^{2},\\&u,u+a_3v-\frac{1}{2}v^{2},v(1+u+a_3v-\frac{1}{2}v^{2}),v,w); u,v,w \in \mathbb R\}, a_3 \in \mathbb R, \end{aligned}$$

respectively

$$\begin{aligned} A_4=B_4=\{g(-w,u,a_1u+v,1-e^{v}+a_1w+(a_1u+v)^{2},v,w); u, v, w \in \mathbb R\}, a_1\ne 0, \end{aligned}$$

are $K_{3}$-connected, respectively $K_4$-connected left transversals in $G_3$, respectively in $G_4$. The sets $A_5=B_5=$

$$\begin{aligned} \{g(1-e^{v}+2auv-\frac{1}{2}a_2u^{2}-aa_2v+ua_2^{2},av+\frac{1}{2}u^{2}-ua_2,u,u,v,w); u,v,w \in \mathbb R\}, \end{aligned}$$

$a_2\in \mathbb R$, are $K_5$-connected left transversals in $G_{5}^{a}$. The sets

$$\begin{aligned}&A_6 =\{g(e^{u}-e^{u-av-bu},e^{v}-e^{v-u},e^{av+bu-v}-e^{av+bu},u,v,w); u,v,w \in \mathbb R\},\\&B_6 =\{g(e^{k}-e^{k-l},e^{l-al-bk}-e^{l},e^{al+bk}-e^{al+bk-k},k,l,m); k,l,m \in \mathbb R\} \end{aligned}$$

are $K_6$-connected left transversals in $G_{6}^{a^2+b^2\ne 0}$. The sets $A_7=B_7=$

$$\begin{aligned} \{g(ve^{au+v-u},1-e^{u}-(a_3-v)(e^{u}-e^{u-au-v}),e^{u}-e^{u-au-v},u,v,w); u,v,w \in \mathbb R\}, \end{aligned}$$

$a_3 \in \mathbb R$, are $K_7$-connected left transversals in $G_{7}^{a}$. The sets

$$\begin{aligned}&A_{8,1}=B_{8,1}=\{g(e^{av+bu-u}\sin (v), \\&\frac{1}{1\!+\!a_3^{2}}(e^{u}(1\!-\!e^{-av-bu})(\sin (v)\!+\!a_3 \cos (v))\!+\!(e^{u}\!-\! \cos (v))(\cos (v)\!-\!a_3 \sin (v))),\\ \\&\frac{1}{1\!+\!a_{3}^{2}}((e^{u}\!-\!\cos (v))(\sin (v)\!+\!a_3 \cos (v))\!-\!(e^{u}\!-\!e^{u-av-bu})(\cos (v)\!-\!a_3 \sin (v))), \\&u,v,w); u, v, w \in \mathbb R\}, a_3\in \mathbb R, \end{aligned}$$

respectively

$$\begin{aligned}&A_{8,2}\!=\!B_{8,2}\!=\!\{g(e^{av+bu-u}\sin (v),(e^{u}\!-\!e^{u-av-bu})\cos (v)-(e^{u}\!-\!\cos (v))\sin (v),\\ \\&(e^{u}-e^{u-av-bu})\sin (v)+(e^{u}-\cos (v))\cos (v),u,v,w); u, v, w \in \mathbb R\}, \end{aligned}$$

are $K_{8,1}$-, respectively $K_{8,2}$-connected left transversals in $G_{8}^{a^2+b^2\ne 0}$. The sets

$$\begin{aligned}&A_{9}=\{g(u,v+(1-e^{-w})(a_2+v),1-e^{-w},v,-\frac{1}{2}v^{2}e^{w},w),u,v,w \in \mathbb R\},\\&B_{9}=\{g(k,l+(e^{-m}-1)(a_2+l),e^{-m}-1,l,\frac{1}{2}l^{2}e^{m},m),k,l,m \in \mathbb R\}, \end{aligned}$$

$a_2\in \mathbb R$, respectively

$$\begin{aligned}&A_{10}=\{g(ve^{v},u,1-e^{-w},v,e^{w}-e^{w-v},w), u,v,w \in \mathbb R\}, \\&B_{10}=\{g(e^{l}-e^{l-m},k,e^{-l}-1,l,-le^{m},m), k,l,m \in \mathbb R\} \end{aligned}$$

are $K_9$-connected, respectively $K_{10}$-connected left transversals in $G_9$, respectively in $G_{10}$. The sets

$$\begin{aligned}&A_{11,1}=\{g(u,-we^{-w},v,e^{w}+vwe^{w}-1,ve^{w},w), u,v,w \in \mathbb R\}, \\&B_{11,1}=\{g(k,me^{-m},l,e^{m}-mle^{m}-1,-le^{m},m), k,l,m \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{11,2}=\{g(u,v,we^{-w},e^{w}+vwe^{w}-1,ve^{w},w), u,v,w \in \mathbb R\}, \\&B_{11,2}=\{g(k,l,-me^{-m},e^{m}-mle^{m}-1,-le^{m},m), k,l,m \in \mathbb R\} \end{aligned}$$

are $K_{11,1}$-, respectively $K_{11,2}$-connected left transversals in $G_{11}$. The sets

$$\begin{aligned}&A_{12,1}=\{g(u,e^{-w}-1,v,ve^{w}-u,u,w), u,v,w \in \mathbb R\}, \\&B_{12,1}=\{g(k,1-e^{-m},l,-le^{m}-k,k,m), k,l,m \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{12,2}=\{g(u,v,1-e^{-w},ve^{w}-u,u,w), u,v,w \in \mathbb R\}, \\&B_{12,2}=\{g(k,l,e^{-m}-1,-le^{m}-k,k,m), k,l,m \in \mathbb R\} \end{aligned}$$

are $K_{12,1}$-, respectively $K_{12,2}$-connected left transversals in $G_{12}$. The sets

$$\begin{aligned}&A_{13,1}=\{g(u,1-e^{w},v,-ve^{w},e^{-w}-e^{-2w},w); u, v, w \in \mathbb R\}, \\&B_{13,1}=\{g(k,e^{-m}-1,l,e^{m}-e^{2m},le^{-m},m); k, l, m \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{13,2}=\{g(u,v,e^{w}-1,-ve^{w},e^{-w}-e^{-2w},w); u, v, w \in \mathbb R\}, \\&B_{13,2}=\{g(k,l,1-e^{-m},e^{m}-e^{2m},le^{-m},m); k, l, m \in \mathbb R\} \end{aligned}$$

are $K_{13,1}$-, respectively $K_{13,2}$-connected left transversals in $G_{13}^{h=-1}$ and the sets

$$\begin{aligned}&A_{13,3}=\{g(u,1-e^{-w},v,e^{w}-e^{w-hw},-ve^{hw},w); u, v, w \in \mathbb R\}, \\&B_{13,3}=\{g(k,e^{-hm}-1,l,le^{m},e^{hm}-e^{hm-m},m); k, l, m \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{13,4}=\{g(u,v,e^{-w}-1,e^{w}-e^{w-hw},-ve^{hw},w); u, v, w \in \mathbb R\}, \\&B_{13,4}=\{g(k,l,1-e^{-hm},le^{m},e^{hm}-e^{hm-m},m); k, l, m \in \mathbb R\} \end{aligned}$$

are $K_{13,1}$-, respectively $K_{13,2}$-connected left transversals in $G_{13}^{-1<h<1}$. The sets

$$\begin{aligned}&A_{14,1}=B_{14,1}=\{g(u,e^{-pw}\sin (w), v,\\&\frac{1}{a_{3}^{2}+1}(e^{pw}v(\sin (w)-a_3 \cos (w))+(\cos (w)-e^{pw})(\cos (w)+a_3 \sin (w))),\\&\frac{1}{a_{3}^{2}+1}(e^{pw}v(a_3 \sin (w)+\cos (w))+(\cos (w)-e^{pw})(a_3 \cos (w)- \sin (w))),w);\\&u, v, w \in \mathbb R \}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{14,2}=B_{14,2}=\{g(u,v,-e^{-pw}\sin (w), \\&\frac{1}{a_{3}^{2}+1}(e^{pw}v(\sin (w)-a_3 \cos (w))+(\cos (w)-e^{pw})(\cos (w)+a_3\sin (w))),\\&\frac{1}{a_{3}^{2}+1}(e^{pw}v(a_3\sin (w)+\cos (w))+(\cos (w)-e^{pw})(a_3\cos (w)-\sin (w))),w); \\&u, v, w \in \mathbb R\}, a_3\ne 0, \end{aligned}$$

are $K_{14,1}$-, respectively $K_{14,2}$-connected left transversals in $G_{14}^{p\ne 0}$, and the sets

$$\begin{aligned}&A_{14,3}=B_{14,3}=\{g(u,e^{-pw}\sin (w),v,\sin (w)(\cos (w)-e^{pw})-e^{pw}v \cos (w),\\&e^{pw}v \sin (w)+\cos (w)(\cos (w)-e^{pw}),w); u, v, w \in \mathbb R\}, \end{aligned}$$

respectively

$$\begin{aligned}&A_{14,4}=B_{14,4}=\{g(u,v,-e^{-pw}\sin (w),\sin (w)(\cos (w)-e^{pw})-e^{pw}v\cos (w),\\&e^{pw}v\sin (w)+\cos (w)(\cos (w)-e^{pw}),w); u, v, w \in \mathbb R\} \end{aligned}$$

are $K_{14,3}$-, respectively $K_{14,4}$-connected left transversals in $G_{14}^{p\ne 0}$. The sets

$$\begin{aligned}&A_{15}=\{g(e^{u-w}-e^{u}+v,u,v,e^{w}-e^{w-u}+w^{2},w,w), u,v,w \in \mathbb R\}, \\&B_{15}=\{g(e^{k}-e^{k-m}+l,k,l,e^{m-k}-e^{m}+m^{2},m,m), k,l,m \in \mathbb R\} \end{aligned}$$

are $K_{15}$-connected left transversals in $G_{15}$. The sets

$$\begin{aligned} A_{16}=B_{16}=\{g(e^{u}+v-1,u,v,e^{w}-u-1,u,w), u,v,w \in \mathbb R\} \end{aligned}$$

are $K_{16}$-connected left transversals in $G_{16}$. The sets

$$\begin{aligned}&A_{17}=\{g(e^{u-hw}-e^{u}+v,u,v,e^{w}-e^{w-u},e^{hw}-e^{hw-w},w); u, v, w \in \mathbb R\}, \\&B_{17}=\{g(e^{k}-e^{k-m}+l,k,l,e^{m}-e^{m-hm},e^{hm-k}-e^{hm},m); k, l, m \in \mathbb R\} \end{aligned}$$

are $K_{17}$-connected left transversals in $G_{17}^{-1\le h<1}$. The sets

$$\begin{aligned}&A_{18,1}=B_{18,1}=\{g(e^{u}+v-1,u,v,\frac{1}{1+a_3^{2}}(1-e^{pw}(a_3 \sin (w)+\cos (w))),\\&\frac{1}{1+a_{3}^{2}}(a_3-e^{pw}(a_3 \cos (w)-\sin (w))),w); u, v, w \in \mathbb R\}, a_3\in \mathbb R, \end{aligned}$$

respectively

$$\begin{aligned}&A_{18,2}=B_{18,2}=\{g(e^{u}+v-1,u,v,e^{pw} \sin (w)-2 \cos (w) \sin (w),\\&\sin (w)^{2}+\cos (w)(e^{pw}-\cos (w)),w); u, v, w \in \mathbb R\}, \end{aligned}$$

are $K_{18,1}$-, respectively $K_{18,2}$-connected left transversals in $G_{18}^{p\ne 0}$.

For all $i=1,\cdots , 18$, the set $A_i \cup B_i$ generates the group $G_i$. By Proposition 1 the assertion is proved. $\square$

5 The Case dim(Z)=2

In this section we obtain the 6-dimensional decomposable solvable Lie groups with 2-dimensional centre which can be represented as multiplication groups of 3-dimensional connected simply connected topological proper loops L. These loops have a 2-dimensional centre Z(L) isomorphic to $\mathbb R^2$ such that the factor loops L/Z(L) are isomorphic to $\mathbb R$.

Proposition 5

Let L be a simply connected topological proper loop of dimension 3 such that its multiplication group is an at most 6-dimensional decomposable nilpotent Lie group. Then the loop L is centrally nilpotent of class 2 and either the group $\mathbb R \times \mathcal {F}_4$ or $\mathbb R \times \mathcal {F}_5$ is the multiplication group of L.

Proof

Each nilpotent Lie group has a centre of dimension $\ge 1$. Hence, if the group Mult(L) is decomposable and nilpotent, then it has a 2-dimensional centre and the loop L has nilpotency class 2 (cf. Lemma 3 a), e)). According to the list of Lie algebras in [14], §5, and [15], p. 100, the Lie algebra of the group Mult(L) is either the direct sum $\mathbf{g}_{3,1} \oplus \mathbf{g}_{3,1}$, where $\mathbf{g}_{3,1}$ is the 3-dimensional nilpotent non-abelian Lie algebra, or $\mathbb R \oplus \mathbf{f}_n$, $n=4,5$, or $\mathbb R \oplus \mathbf{g}_{5,i}$, $i=4,5,6$. By Lemma 3 e) the Lie algebra of Mult(L) has a 5-dimensional abelian ideal containing its centre and its commutator subalgebra. Since there does not exist any such ideal for the Lie algebras $\mathbf{g}_{3,1} \oplus \mathbf{g}_{3,1}$ and $\mathbb R \oplus \mathbf{g}_{5,i}$, $i=4,5,6$, these Lie algebras are excluded. Now the assertion follows from Proposition 5.1. in [6], pp. 400-406. $\square$

Proposition 6

Let L be a connected topological loop of dimension 3 such that the Lie algebra $\mathbf{g}$ of its multiplication group is a 6-dimensional decomposable solvable non-nilpotent Lie algebra with 2-dimensional centre. Then L is centrally nilpotent of class 2. Moreover, the following Lie algebra pairs can occur as the Lie algebra $\mathbf{g}$ of the group Mult(L) and the subalgebra $\mathbf {k}$ of the subgroup Inn(L):

If $\mathbf{g}_i=\mathbb {R}^{2}\oplus \mathbf{n}_i=\langle f_1, f_2 \rangle \oplus \langle e_1, \cdots , e_4 \rangle$ such that $\mathbf{n}_i$, $i=1,\cdots ,4$, is a 4-dimensional solvable indecomposable Lie algebra with trivial centre, then one has

• $\mathbf{n}_{1}=\mathbf{g}_{4,2}^{\alpha \ne 0}$: $[e_1,e_4]=\alpha e_1, [e_2,e_4]=e_2, [e_3,e_4]=e_2+e_3$, $\mathbf{k}_1=\langle e_{1}+f_{1},e_{2}+f_{1},e_{3}\rangle$,

• $\mathbf{n}_{2}=\mathbf{g}_{4,4}$: $[e_1,e_4]=e_1, [e_2,e_4]=e_1+e_2,[e_3,e_4]=e_2+e_3$, $\mathbf{k}_2=\langle e_{1}+f_{1},e_{2}+a_{2}f_{1},e_{3}+a_{3}f_{1}\rangle$, $a_2,a_3\in \mathbb {R}$,

• $\mathbf{n}_{3}=\mathbf{g}_{4,5}^{-1\le \gamma \le \beta \le 1,\gamma \beta \ne 0}$: $[e_1,e_4]=e_1, [e_2,e_4]=\beta e_2, [e_3,e_4]=\gamma e_3$, $\mathbf{k}_3=\langle e_{1}+f_{1},e_{2}+f_{1},e_{3}+f_{1}\rangle$,

• $\mathbf{n}_{4}=\mathbf{g}_{4,6}^{p\ge 0,\alpha \ne 0}$: $[e_1,e_4]=\alpha e_1, [e_2,e_4]=pe_2-e_3, [e_3,e_4]=e_2+pe_3$, $\mathbf{k}_{4,1}=\langle e_{1}+f_{1},e_{2}+f_{1},e_{3}+a_3f_1\rangle$, $a_3\in \mathbb {R}$, $\mathbf{k}_{4,2}=\langle e_{1}+f_{1},e_{2},e_{3}+f_1\rangle$.

If $\mathbf{g}_j=\mathbb {R}\oplus \mathbf{h}_j=\langle f_{1}\rangle \oplus \langle e_{1},e_{2}, e_{3},e_{4}, e_{5}\rangle$, where $\mathbf{h}_j$, $j=5, \cdots , 8$, is a 5-dimensional solvable indecomposable Lie algebra with 1-dimensional centre, then one has

• $\mathbf{h}_{5}=\mathbf{g}_{5,8}^{0<|\gamma |\le 1}$: $[e_2,e_5]=e_1, [e_3,e_5]=e_3,[e_4,e_5]=\gamma e_4$, $\mathbf{k}_{5,\epsilon }=\langle e_{2}+\epsilon f_1,e_{3}+e_{1},e_{4}+e_{1}\rangle$, $\epsilon =0,1$,

• $\mathbf{h}_{6}=\mathbf{g}_{5,10}$: $[e_2,e_5]=e_1, [e_3,e_5]=e_2,[e_4,e_5]=e_4$, $\mathbf{k}_{6,\epsilon }=\langle e_{2},e_{3}+\epsilon f_1,e_{4}+e_{1}\rangle$, $\epsilon =0,1$, $\mathbf{k}_{6,2}=\langle e_{2}+b_1f_1,e_{3}+b_2f_1,e_{4}+f_{1}+ae_1\rangle$, $b_1, b_2 \in \mathbb R$, $a\ne 0$,

• $\mathbf{h}_{7}=\mathbf{g}_{5,14}^{p\ne 0}$: $[e_2,e_5]=e_1, [e_3,e_5]=pe_3-e_4,[e_4,e_5]=e_3+pe_4$, $\mathbf{k}_{7,1}^{\epsilon }=\langle e_{2}+\epsilon f_1,e_{3}+e_{1},e_{4}+a_{3}e_{1}\rangle$, $\mathbf{k}_{7,2}^{\epsilon }=\langle e_{2}+\epsilon f_1,e_{3},e_{4}+e_{1}\rangle$, $\epsilon =0,1$, $a_3\in \mathbb {R}$,

• $\mathbf{h}_{8}=\mathbf{g}_{5,15}^{\gamma =0}$: $[e_1,e_5]=e_1, [e_2,e_5]=e_1+e_2, [e_4,e_5]=e_3$, $\mathbf{k}_{8,\epsilon }=\langle e_{1}+e_3,e_{2},e_{4}+\epsilon f_1\rangle$, $\epsilon =0,1$.

Proof

By Lemma 2 we may assume that the loop L is simply connected and hence it is homeomorphic to $\mathbb R^{3}$. As the multiplication group Mult(L) of L is a 6-dimensional decomposable solvable Lie group with 2-dimensional centre the loop L has nilpotency class 2 (cf. Lemma 3 a), e)). Furthermore, for the Lie algebra of Mult(L) we have the following possibilities: $\mathbb {R}^{2}\oplus \mathbf{n}$, $\mathbb {R}\oplus \mathbf{h}$, $\mathbf{l}_{2} \oplus \mathbb {R}\oplus \mathbf{g}_{3,1}$, and $\mathbf{l}_{2}\oplus \mathbf{l}_{2}\oplus \mathbb {R}^{2}$, where $\mathbf{n}$ and $\mathbf{h}$ are characterized in the assertion. By [14], §5, for $\mathbf{n}$ we have the Lie algebras $\mathbf{g}_{4,i}$, $i=2,4,5,6,7,10$, $\mathbf{g}_{4,8}^{h\ne -1}$, $\mathbf{g}_{4,9}^{p\ne 0}$. Moreover, the Lie algebras $\mathbf{g}_{5,j}$, $j=8,10,22,29,38,39$, $\mathbf{g}_{5,14}^{p\ne 0}$, $\mathbf{g}_{5,15}^{\gamma =0}$, $\mathbf{g}_{5,19}^{\alpha =-1}$, $\mathbf{g}_{5,20}^{\alpha =-1}$, $\mathbf{g}_{5,28}^{\alpha =-1}$, $\mathbf{g}_{5,25}^{p=0}$, $\mathbf{g}_{5,26}^{p=0}$ and $\mathbf{g}_{5,30}^{h=-2}$ can be considered as $\mathbf{h}$ (cf. [15], §10, p. 105-106).

If these Lie algebras were the Lie algebra of the multiplication group of L, then they would have a 5-dimensional abelian ideal containing their commutator ideal and their centre (cf. Lemma 3 e)). Since the Lie algebras $\mathbf{l}_{2}\oplus \mathbb {R}\oplus \mathbf{g}_{3,1}$, $\mathbf{l}_{2}\oplus \mathbf{l}_{2} \oplus \mathbb {R}^{2}$, $\mathbb R^2 \oplus \mathbf{g}_{4,j}$, $j=7,10$, $\mathbb R^2 \oplus \mathbf{g}_{4,8}^{h \ne -1}$, $\mathbb R^2 \oplus \mathbf{g}_{4,9}^{p \ne 0}$, $\mathbb R \oplus \mathbf{g}_{5,r}^{\alpha =-1}$, $r=19,20,28$, $\mathbb R \oplus \mathbf{g}^{p=0}_{5,l}$, $l=25,26$, $\mathbb R \oplus \mathbf{g}_{5,30}^{h=-2}$, $\mathbb R \oplus \mathbf{g}_{5,p}$, $p=22,29,38,39$, do not contain any 5-dimensional abelian ideal, these Lie algebras are not the Lie algebra of the group Mult(L) of L. Hence it remains to deal with the Lie algebras $\mathbf{g}_{i}$, $i=1, \cdots , 8$ in the assertion.

The 1-dimensional central subalgebras of $\mathbf{g}_{i}$, $i=1,2,3,4$, are $\mathbf{i}_{1}=\langle f_{2} \rangle$ and $\mathbf{i}_{2}=\langle f_{1}+a f_{2}\rangle$, $a\in \mathbb {R}$, those of $\mathbf{g}_{j}$, $j=5,6,7$, are $\mathbf{i}_{3}=\langle f_{1}+be_{1}\rangle$, $b \in \mathbb R$, and $\mathbf{i}_{4}=\langle e_{1}\rangle$, whereas those of $\mathbf{g}_{8}$ are $\mathbf{i}_{5}=\langle f_{1}+c e_{3}\rangle$, $c\in \mathbb {R}$, and $\mathbf{i}_{6}=\langle e_{3}\rangle$. With the exception of the Lie algebra $\mathbf{g}_{6}$, for every ideal $\mathbf{s}$ of each Lie algebra $\mathbf{g}_{i}$, $i=1,\cdots , 8$, such that $\mathbf{s}$ contains a 1-dimensional central subalgebra of $\mathbf{g}_{i}$ the factor Lie algebras $\mathbf{g}_{i}/\mathbf{s}$ are not isomorphic to $\mathbf{f}_{4}$. The Lie algebra $\mathbf{g}_{6}$ has the ideal $\mathbf{s}=\langle f_1+b e_1,e_4\rangle$ containing $\mathbf{i}_{3}$ such that the factor Lie algebra $\mathbf{g}_{6}/\mathbf{s}$ is isomorphic to $\mathbf{f}_{4}$.

According to Lemma 3 e) the simply connected Lie groups $G_i$ of $\mathbf{g}_{i}$, $i=1,\cdots ,8$, has a 1-dimensional connected central subgroup $N_d=\exp {\mathbf{n}_{d}}$, $d=1,2$, $4,\cdots ,6$, such that the orbit $N_d(e)$ is isomorphic to $\mathbb {R}$ and the factor loop $L/N_d(e)$ is isomorphic to $\mathbb {R}^{2}$. By Lemma 4 a) (i) the Lie algebras $\mathbf{g}_{i}$, $i=1, \cdots , 8$, have a 4-dimensional abelian ideal $\mathbf{p}$ containing only a 1-dimensional central subalgebra $\mathbf{n}_{d}$ of $\mathbf{g}_{i}$ and the Lie algebra $\mathbf{k}$ of the inner mapping group Inn(L) of L such that $\mathbf{g}_i' \subset \mathbf{p}$ and $\mathbf{k}$ has the properties as in 3. of Lemma 1. Then for the triples $(\mathbf{g}_i,\mathbf{p},\mathbf{k})$ we obtain:

(a) For the Lie algebras $\mathbf{g}_{i}$, $i=1,2,3,4$, the ideal $\mathbf{p}$ has one of the following forms $\mathbf{p}_{a}=\langle f_{1}+af_{2},e_{1},e_{2},e_{3}\rangle$, $a \in \mathbb R$ and $\widetilde{\mathbf{p}}=\langle f_{2},e_{1},e_{2},e_{3}\rangle$. Hence for the subalgebra $\mathbf{k}$ one has $\mathbf{k}_{a}=\langle e_{1}+a_{1}(f_{1}+af_{2}),e_{2}+a_{2}(f_{1}+af_{2}),e_{3}+a_{3}(f_{1}+af_{2})\rangle$, $a \in \mathbb R$ and $\widetilde{\mathbf{k}}=\langle e_{1}+a_{1}f_{2},e_{2}+a_{2}f_{2},e_{3}+a_{3}f_{2}\rangle$, where $a_i \in \mathbb {R}$, $i=1,2,3$. Using the automorphism $\phi (f_{1})=f_{2}$, $\phi (f_{2})=f_1+af_{2}$, $\phi (e_{i})=e_{i}$, $i=1,2,3,4$, the Lie algebra $\widetilde{\mathbf{k}}$ reduces to $\mathbf{k}_a$. So it remains to consider the subalgebra $\mathbf{k}_a$, such that

in the case of the Lie algebra $\mathbf{g}_1$: $a_1a_2\ne 0$ since $\langle e_{1}\rangle$ and $\langle e_{2}\rangle$ are ideals of $\mathbf{g}_1$,

in the case of $\mathbf{g}_2$: $a_1\ne 0$ because $\langle e_{1}\rangle$ is an ideal of $\mathbf{g}_2$,

in the case of $\mathbf{g}_3$: $a_1a_2a_3\ne 0$ since $\langle e_{1}\rangle$, $\langle e_{2}\rangle$ and $\langle e_{3}\rangle$ are ideals of $\mathbf{g}_3$,

in the case of $\mathbf{g}_4$: $a_1\ne 0$ and at least one of $\{a_2, a_3\}$ is different from 0 because $\langle e_{1}\rangle$ and $\langle e_{2},e_{3}\rangle$ are ideals of $\mathbf{g}_4$.

Using the automorphism $\phi (f_{1})=f_{1}-af_{2}$, $\phi (f_{2})=f_{2}$, $\phi (e_{1})=a_{1}e_{1}$, $\phi (e_{2})=a_{2}e_{2}$, $\phi (e_{3})=a_{2}e_{3}+a_{3}e_{2}$ and $\phi (e_{4})=e_{4}$ for $\mathbf{g}_1$, respectively $\phi (e_{j})=a_{1}e_{j}$, $j=2,3$ for $\mathbf{g}_2$, respectively $\phi (e_{3})=a_{3}e_{3}$ for $\mathbf{g}_3$, the Lie algebra $\mathbf{k}_a$ reduces to $\mathbf{k}_1$, respectively to $\mathbf{k}_2$, $a_2,a_3\in \mathbb R$, respectively to $\mathbf{k}_3$ in the assertion. Applying the automorphism $\phi (f_{1})=f_{1}-af_{2}$, $\phi (f_{2})=f_{2}$, $\phi (e_{1})=a_{1}e_{1}$, $\phi (e_{j})=a_{2}e_{j}$, $j=2,3$ and $\phi (e_{4})=e_{4}$ for $\mathbf{g}_4$ if $a_2\ne 0$, respectively $\phi (e_{j})=a_{3}e_{j}$, $j=2,3$ if $a_2=0$ and $a_3\ne 0$, we can reduce $\mathbf{k}_a$ to $\mathbf{k}_{4,1}$, $a_3\in \mathbb {R}$, respectively to $\mathbf{k}_{4,2}$ in the assertion.

(b) For the Lie algebras $\mathbf{g}_j$, $j=5,7$, the ideal $\mathbf {p}$ has one of the following shapes $\mathbf{p}_a=\langle e_{1},f_1+a e_{2},e_{3},e_{4}\rangle$, $a\in \mathbb {R}\backslash \{0\}$, $\widetilde{\mathbf{p}}=\langle e_{1},e_{2},e_{3},e_{4}\rangle$. Hence the subalgebras $\mathbf{k}$ are $\mathbf{k}_a=\langle f_1+a e_{2}+a_{1}e_{1},e_{3}+a_{2}e_{1},e_{4}+a_{3}e_{1}\rangle$, $a\in \mathbb {R}\backslash \{0\}$, and $\widetilde{\mathbf{k}}=\langle e_{2}+a_{1}e_{1},e_{3}+a_{2}e_{1},e_{4}+a_{3}e_{1}\rangle$, $a_i\in \mathbb {R}$, $i=1,2,3$, such that

for $\mathbf{g}_5$: $a_2a_3\ne 0$ since $\langle e_{3}\rangle$, $\langle e_{4}\rangle$ are ideals of $\mathbf{g}_5$, and

for $\mathbf{g}_7$: $a_2\ne 0$ or $a_3\ne 0$ because $\langle e_{3}, e_{4}\rangle$ is an ideal of $\mathbf{g}_7$.

The automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=e_{i}$, $i=1,5$, $\phi (e_{2})=e_{2}-a_{1}e_{1}$, $\phi (e_{3})=a_{2}e_{3}$ and $\phi (e_{4})=a_{3}e_{4}$, respectively $\phi (f_{1})=af_{1}-a_1e_1$, $\phi (e_{2})=e_{2}$ of $\mathbf{g}_5$ maps the subalgebra $\widetilde{\mathbf{k}}$ onto $\mathbf{k}_{5,0}$, respectively the subalgebra $\mathbf{k}_a$ onto $\mathbf{k}_{5,1}$ in the assertion. If $a_2\ne 0$, then the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=e_{i}$, $i=1,5$, $\phi (e_{2})=e_{2}-a_{1}e_{1}$, $\phi (e_{j})=a_{2}e_{j}$, $j=3,4$, respectively $\phi (f_{1})=af_{1}-a_1e_1$, $\phi (e_{2})=e_{2}$ of the Lie algebra $\mathbf{g}_7$ reduces the subalgebra $\widetilde{\mathbf{k}}$ to $\mathbf{k}_{7,1}^0$, respectively the subalgebra $\mathbf{k}_a$ to $\mathbf{k}_{7,1}^1$ in the assertion. If $a_2=0$ and $a_3\ne 0$, then using the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=e_{i}$, $i=1,5$, $\phi (e_{2})=e_{2}-a_{1}e_{1}$, $\phi (e_{j})=a_{3}e_{j}$, $j=3,4$, respectively $\phi (f_{1})=af_{1}-a_1e_1$, $\phi (e_{2})=e_{2}$ of $\mathbf{g}_7$ we can change the subalgebra $\widetilde{\mathbf{k}}$ to $\mathbf{k}_{7,2}^0$, respectively the subalgebra $\mathbf{k}_a$ to $\mathbf{k}_{7,2}^1$ in the assertion.

(c) For the Lie algebra $\mathbf{g}_8$ the ideal $\mathbf{p}$ has one of the following forms $\widetilde{\mathbf{p}}=\langle e_{1},e_{2},e_{3},e_{4}\rangle$, $\mathbf{p}_a=\langle e_{1},e_{2},e_{3},f_1+a e_{4}\rangle$, $a\in \mathbb {R}\backslash \{0\}$. Therefore for the subalgebra $\mathbf{k}$ one has $\widetilde{\mathbf{k}}=\langle e_{1}+a_{1}e_{3},e_{2}+a_{2}e_{3},e_{4}+a_{3}e_{3}\rangle$, $\mathbf{k}_a=\langle e_{1}+a_{1}e_{3},e_{2}+a_{2}e_{3},f_{1}+a e_4+a_{3}e_{3}\rangle$, $a\in \mathbb {R}\backslash \{0\}, a_i\in \mathbb {R}$, $i=1,2,3$, such that $a_1\ne 0$ since $\langle e_{1}\rangle$ is an ideal of $\mathbf{g}_8$. The automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=e_{i}$, $i=3,5$, $\phi (e_{1})=a_1e_1$, $\phi (e_{2})=a_1e_{2}-a_{2}e_{1}$, and $\phi (e_{4})=e_4-a_{3}e_{3}$, respectively $\phi (f_{1})=af_{1}-a_3e_3$, $\phi (e_{4})=e_4$, maps the subalgebra $\widetilde{\mathbf{k}}$ onto $\mathbf{k}_{8,0}$, respectively $\mathbf{k}_a$ onto $\mathbf{k}_{8,1}$ of the assertion.

(d) If the Lie algebra $\mathbf{g}_6$ is the Lie algebra of the group Mult(L) of L, then the factor loop $L/I_4(e)$, where $I_4=\exp (\mathbf{i}_4)$, is isomorphic to $\mathbb R^2$. Hence the Lie algebra $\mathbf{k}$ of the group Inn(L) of L is a subalgebra of the ideal $\mathbf{p}$ having one of the following forms $\widetilde{\mathbf{p}}=\langle e_{1},e_{2},e_{4},e_{3}\rangle$, $\mathbf{p}_a=\langle e_{1},e_{2},e_{4},f_1+ae_{3}\rangle$, $a\in \mathbb R\backslash \{0\}$. Therefore we obtain the subalgebras $\widetilde{\mathbf{k}}=\langle e_{2}+a_{1}e_{1},e_{3}+a_{2}e_{1},e_{4}+a_{3}e_{1}\rangle$, $\mathbf{k}_a=\langle e_{2}+a_{1}e_{1},f_1+a e_{3}+a_{2}e_{1},e_{4}+a_{3}e_{1}\rangle$, where $a\in \mathbb {R}\backslash \{0\}, a_i\in \mathbb R$, $i=1,2$, and $a_3\ne 0$ since $\langle e_{4}\rangle$ is an ideal of $\mathbf{g}_6$. With the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=e_{i}$, $i=1,5$, $\phi (e_{2})=e_{2}-a_{1}e_{1}$, $\phi (e_{3})=e_3-a_{1}e_{2}-a_2e_1$ and $\phi (e_{4})=a_{3}e_{4}$, respectively $\phi (f_{1})=af_{1}-a_2e_1$, $\phi (e_{3})=e_3-a_{1}e_{2}$, we can change the subalgebra $\widetilde{\mathbf{k}}$ onto $\mathbf{k}_{6,0}$, respectively $\mathbf{k}_a$ onto $\mathbf{k}_{6,1}$ in the assertion.

Since for the ideal $\mathbf{s}=\langle f_{1}+be_{1}, e_4\rangle$, $b\in \mathbb {R}$, of $\mathbf{g}_6$, the factor Lie algebra $\mathbf{g}_6/\mathbf{s}$ is isomorphic to $\mathbf{f}_4$, the factor loop $L/I_{3}(e)$, where $I_3=\exp (\mathbf{i}_3)$, is isomorphic to an elementary filiform loop $L_{\mathcal F}$. The orbit S(e), where $S=\exp (s)$, coincides with $I_{3}(e)$ (cf. Lemma 3 e). Hence the Lie algebra $\mathbf{k}$ contains the basis element $e_4+a_3(f_1+ae_1)$, $a_3\in \mathbb {R}\backslash \{0\}$. Since $\mathbf{k}$ is a 3-dimensional subalgebra of the 5-dimensional abelian ideal $\mathbf{v}=\langle f_{1},e_{1},e_{2},e_{3},e_4\rangle$, it has the form $\mathbf{k}=\langle e_{2}+b_1 f_1+a_1 e_1, e_{3}+b_2f_1+ a_2e_1, e_{4}+a_3(f_1+ae_{1})\rangle$, $a, a_i, b_i \in \mathbb {R}$, $i=1,2,3$, $aa_3\ne 0$. Using the automorphism $\phi (f_{1})=f_{1}$, $\phi (e_{i})=e_{i}$, $i=1,5$, $\phi (e_2)=e_2-a_1e_1$, $\phi (e_3)=e_3-a_1e_2-a_2e_1$ and $\phi (e_{4})=a_{3}e_{4}$, the subalgebra $\mathbf{k}$ reduces to $\mathbf{k}_{6,2}=\langle e_{2}+b_1f_1,e_{3}+b_2f_1,e_{4}+f_{1}+ae_1\rangle$. This proves the assertion. $\square$

Using ([23], §4) we obtain:

Lemma 6

The linear representation of the simply connected Lie group $G_i$ and its subgroup $K_i$ corresponding to the Lie algebra $\mathbf{g}_i$ and its subalgebra $\mathbf{k}_i$, $i=1,...,8$, is given by the multiplication:

For $i=1$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad =\! g(x_1\!+\!y_1e^{ax_4},x_2\!+\!(y_2\!+\!x_4y_3)e^{x_4},x_3\!+\!y_3e^{x_4},x_4\!+\!y_4,x_5\!+\!y_5,x_6\!+\!y_6), a\!\ne \! 0,\\&K_{1}=\{g(u_1,u_2,u_3,0,u_1+u_2,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

For $i=2$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)\!=\!g(x_1\!+\!(y_1+x_4y_2+\frac{1}{2}x_4^{2}y_3)e^{x_4}, \\&x_2+(y_2+x_4y_3)e^{x_4},x_3+y_3e^{x_4},x_4+y_4,x_5+y_5,x_6+y_6), \\&K_{2}=\{g(u_1,u_2,u_3,0,u_1+a_2u_2+a_3u_3,0);u_i \in \mathbb R, i=1,2,3 \}, a_2,a_3 \in \mathbb R, \end{aligned}$$

For $i=3$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad = g(x_1+y_1e^{x_4},x_2+y_2e^{ax_4},x_3\\&\qquad +y_3e^{bx_4},x_4+y_4,x_5+y_5,x_6+y_6), -1 \le a \le b \le 1, \\&ab\ne 0, K_{3}=\{g(u_1,u_2,u_3,0,u_1+u_2+u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

For $i=4$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6)g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+y_1e^{ax_4}, \\&x_2+(y_2 \cos (x_4)+y_3 \sin (x_4))e^{bx_4},x_3+(y_3 \cos (x_4)-y_2 \sin (x_4))e^{bx_4}, \\&x_4+y_4,x_5+y_5,x_6+y_6), a\ne 0, b\ge 0, \\&K_{4,1}=\{g(u_1,u_2,u_3,0,u_1+u_2+a_3u_3,0);u_i \in \mathbb R, i=1,2,3 \}, a_3 \in \mathbb R,\\&K_{4,2}=\{g(u_1,u_2,u_3,0,u_1+u_3,0); u_i \in \mathbb R, i=1,2,3 \}, \end{aligned}$$

For $i=5$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad = g(x_1+y_1+x_5y_2,x_2+y_2,x_3+y_3e^{x_5},x_4\\&\qquad +y_4e^{cx_5},x_5+y_5,x_6+y_6), 0 < |c| \le 1, \\&K_{5,\epsilon }=\{g(u_2+u_3,u_1,u_2,u_3,0,\epsilon u_1); u_i \in \mathbb R, i=1,2,3 \}, \epsilon =0,1, \end{aligned}$$

For $i=6$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&g(x_1+y_1+x_5y_2\!+\!\frac{1}{2}x_{5}^2y_3,x_2\!+\!y_2\!+\!x_5y_3,x_3\!+\!y_3,x_4\!+\!y_4e^{x_5},x_5\!+\!y_5,x_6+y_6), \\&K_{6,\epsilon }=\{g(u_3,u_1,u_2,u_3,0,\epsilon u_2); u_i \in \mathbb R, i=1,2,3 \}, \epsilon =0,1, \\&K_{6,2}=\!\{g(au_3,u_1,u_2,u_3,0,b_1u_1\!+\!b_2u_2\!+\!u_3); u_i \in \mathbb R, i\!=\!1,2,3\}, b_j \!\in \! \mathbb R, a\!\ne \! 0, \end{aligned}$$

For $i=7$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6)=g(x_1+y_1+x_2y_5,x_2+y_2, \\&x_3+(y_3 \cos (x_5)-y_4 \sin (x_5))e^{px_5},x_4+(y_4 \cos (x_5)+y_3 \sin (x_5))e^{px_5}, \\&x_5+y_5,x_6+y_6), p \ne 0, \\&K_{7,1}^{\epsilon }=\{g(u_2+a_3u_3,u_1,u_2,u_3,0,\epsilon u_1); u_i \in \mathbb R, i=1,2,3 \}, \\&K_{7,2}^{\epsilon }=\{g(u_3,u_1,u_2,u_3,0,\varepsilon u_1); u_i \in \mathbb R, i=1,2,3 \}, \epsilon =0,1, a_3 \in \mathbb R, \end{aligned}$$

For $i=8$

$$\begin{aligned}&g(x_1,x_2,x_3,x_4,x_5,x_6) g(y_1,y_2,y_3,y_4,y_5,y_6) \\&\quad =\!g(x_1\!+\!(y_1\!+\!y_2x_5)e^{x_5},x_2\!+\!y_2e^{x_5},x_3\!+\!y_3+x_5y_4,x_4+y_4,x_5+y_5,x_6+y_6), \\&K_{8,\epsilon }=\{g(u_1,u_2,u_1,u_3,0,\epsilon u_3); u_i \in \mathbb R, i=1,2,3 \}, \epsilon =0,1, \end{aligned}$$

Proposition 7

There does not exist any 3-dimensional connected topological proper loop L having $\mathbf{g}_6$ as the Lie algebra of its multiplication group and the Lie algebra $\mathbf{k}_{6,2}$ as the Lie algebra of its inner mapping group.

Proof

We may assume that L is simply connected and hence it is homeomorphic to $\mathbb R^3$ (cf. Lemma 2). We show that the Lie group $G_6$ does not allow continuous left transversals S and T to the subgroup $K_{6,2}$ such that for all $s\in S$ and $t\in T$ one has $s^{-1}t^{-1}st \in K_{6,2}$ and the set $S\cup T$ generates $G_6$.

Two arbitrary left transversals to the group $K_{6,2}$ in $G_6$ are:

$$\begin{aligned}&S =\{g(u,h_1(u,v,w),h_2(u,v,w),h_3(u,v,w),v,w); u,v,w \in \mathbb R \}, \\&T =\{g(k,g_1(k,l,m),g_2(k,l,m),g_3(k,l,m),l,m); k,l,m \in \mathbb R \}, \end{aligned}$$

where $h_i(u,v,w): \mathbb R^3 \rightarrow \mathbb R$ and $g_i(k,l,m): \mathbb R^3 \rightarrow \mathbb R$, $i=1,2,3$, are continuous functions with $h_i(0,0,0)= g_i(0,0,0)= 0$. The products $s^{-1}t^{-1}st$, $s \in S$, $t \in T$, are elements of $K_{6,2}$ if and only if the equations

$$\begin{aligned}&a(g_3(k,l,m)e^{-l}(1-e^{-v})-h_3(u,v,w)e^{-v}(1-e^{-l}))=vg_1(k,l,m) \nonumber \\&vlg_2(k,l,m)-lh_1(u,v,w)+lvh_2(u,v,w)\nonumber \\&\quad +\frac{1}{2}l^{2}h_2(u,v,w)-\frac{1}{2}v^{2}g_2(k,l,m), \end{aligned}$$

(12)

$$\begin{aligned}&g_3(k,l,m)e^{-l}(1-e^{-v})-h_3(u,v,w)e^{-v}(1-e^{-l})\nonumber \\&\quad =b_1lh_2(u,v,w)-b_1vg_2(k,l,m) \end{aligned}$$

(13)

are satisfied for all $k,l,m,u,v,w\in \mathbb R$. Applying equation (13), equation (12) becomes simplified to

$$\begin{aligned}&vg_1(k,l,m)+a b_1 vg_2(k,l,m)-vl g_2(k,l,m)-\frac{1}{2} v^2 g_2(k,l,m) \nonumber \\&\quad =lh_1(u,v,w)+ a b_1 l h_2(u,v,w)- lvh_2(u,v,w)-\frac{1}{2}l^{2}h_2(u,v,w). \end{aligned}$$

(14)

Using the new functions $g'_1(k,l,m)=g_1(k,l,m)+ a b_1 g_2(k,l,m)-l g_2(k,l,m)$, $h'_1(u,v,w)=h_1(u,v,w)+ a b_1 h_2(u,v,w)- vh_2(u,v,w)$, equation (14) reduces to

$$\begin{aligned} v g'_1(k,l,m)- \frac{1}{2} v^2 g_2(k,l,m)=l h'_1(u,v,w) -\frac{1}{2}l^{2}h_2(u,v,w). \end{aligned}$$

(15)

Equation (15) holds precisely if the functions $g'_1(k,l,m)$ and $g_2(k,l,m)$, respectively $h'_1(u,v,w)$ and $h_2(u,v,w)$ are polynomials of l, respectively of v with order at most 2. Using this, equation (13) is satisfied if and only if its left hand side and its right hand side are 0. This holds precisely if one has $g_3(l)=c(e^l-1)$ and $h_3(v)=c(e^v-1)$, where c is a real constant. In this case the set $S \cup T$ does not generate the group $G_6$. Hence by Proposition 1 the group $G_6$ and the subgroup $K_{6,2}$ are not the multiplication group and the inner mapping group of L. This proves the assertion. $\square$

Theorem 2

Let L be a simply connected topological proper loop of dimension 3 such that its multiplication group is a 6-dimensional solvable non-nilpotent decomposable Lie group having 2-dimensional centre. Then the pairs of Lie groups $(G_i,K_i)$, $i=1, \cdots , 8$, given in Lemma 6 are the multiplication groups Mult(L) and the inner mapping groups Inn(L) of L with the only exception $(G_6, K_{6,2})$.

Proof

The pairs $(G_i,K_i)$, $i=1, \cdots , 8$, in Lemma 6 can occur as the group Mult(L) and the subgroup Inn(L) of L. According to Proposition 7 the pair $(G_6, K_{6,2})$ is excluded. In all other cases we give continuous left transversals $A_i$, $B_i$ to the subgroup $K_i$, $i=1, \cdots , 8$, which fulfill the requirements of Proposition 1.

Appropriate $K_1$-connected left transversals in the group $G_1^a$ are: for $a<-1$ and for $a>1$ the sets

$$\begin{aligned}&A_{1,1}=\{g(e^{au}(e^{-u}-1),e^{u}(1-e^{-au})+u^{2},u,u,v,w); u, v, w \in \mathbb R\}, \\&B_{1,1}=\{g(e^{ak}(1-e^{-k}),k^{2}-e^{k}(1-e^{-ak}),k,k,l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

for $0<a<1$ and for $-1<a<0$ the sets

$$\begin{aligned}&A_{1,2}\!=\!\{g(-ue^{au-u},1\!-\!e^{u}(1\!-\!u(1-e^{-au})),e^{u}-e^{-au+u},u,v,w); u, v, w \in \mathbb R\}, \\&B_{1,2}=\{g(ke^{ak-k},1-e^{k}(1-k(e^{-ak}-1)),e^{-ak+k}-e^{k},k,l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

for $a=1$ the sets

$$\begin{aligned}&A_{1,3}=\{g(w,e^{u}-1-w+u^{2},u,u,v,w); u, v, w \in \mathbb R\}, \\&B_{1,3}=\{g(l^{2},e^{k}-1-l^{2}+k^{2},k,k,l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

for $a=-1$ the sets

$$\begin{aligned}&A_{1,4}=\{g(ue^{-2u},e^{u}-1-ue^{u}+ue^{2u},e^{2u}-e^{u},u,v,w); u, v, w \in \mathbb R\}, \nonumber \\&B_{1,4}=\{g(-ke^{-2k},e^{k}-1+ke^{k}-ke^{2k},e^{k}-e^{2k},k,l,m); k, l, m \in \mathbb R\}. \end{aligned}$$

Appropriate $K_2$-connected left transversals in $G_2$ are the sets

$$\begin{aligned}&A_2\!=\!\{g(e^{u}\!-\!1\!-\!u^{3}\!+\!\frac{3}{2}a_2u^{2}\!+\!u(a_3\!-\!a_2^{2}),a_2u\!-\!\frac{3}{2}u^{2},-u,u,v,w); u,v,w \in \mathbb R\}, \\&B_2\!=\!\{g(e^{k}-1\!+\!k^{3}-\frac{3}{2}k^{2}a_2\!+\!k(a_2^{2}-a_3),\frac{3}{2}k^{2}\!-\!a_2k,k,k,l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

$a_2, a_3\in \mathbb {R}$. Appropriate $K_3$-connected left transversals in $G_3^{a,b}$ are: for $-1\le a=b\le 1$ the sets

$$\begin{aligned}&A_{3,1}=\{g(e^{u}(e^{-au}-1),e^{au}(1-e^{-u})-w,w,u,v,w); u,v,w \in \mathbb R\}, \\&B_{3,1}=\{g(e^{k}(1-e^{-ak}),e^{ak}(e^{-k}-1)-m,m,k,l,m); k,l,m \in \mathbb R\}, \end{aligned}$$

for $-1\le a<b\le 1$ the sets

$$\begin{aligned}&A_{3,2}=\{g(e^{u-au}-e^{u-bu},e^{au}-e^{au-u},e^{bu-u}-e^{bu},u,v,w); u, v, w \in \mathbb R\}, \\&B_{3,2}=\{g(e^{k-bk}-e^{k-ak},e^{ak-k}-e^{ak},e^{bk}-e^{bk-k},k,l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

where $ab\ne 0$. Appropriate $K_{4,1}$-connected left transversals in $G_4^{a,b}$ are the sets

$$\begin{aligned}&A_{4,1}=B_{4,1}=\{g(e^{au-bu}\sin (u), \\&\frac{1}{a_{3}^{2}\!+\!1}((e^{bu}\!-\!e^{bu-au})(\sin (u)\!-\!a_3\cos (u))\!+\!(e^{bu}\!-\!\cos (u))(\cos (u)+a_3\sin (u))), \\&\frac{1}{a_{3}^{2}\!+\!1}((e^{bu}\!-\!e^{bu-au})(a_3\sin (u)\!+\!\cos (u))\!+\!(e^{bu}\!-\!\cos (u))(a_3\cos (u)\!-\!\sin (u))), \\&u,v,w); u, v, w \in \mathbb R\}, a_3 \in \mathbb R. \end{aligned}$$

Appropriate $K_{4,2}$-connected left transversals in $G_4^{a,b}$ are the sets

$$\begin{aligned}&A_{4,2}=B_{4,2}=\{g(e^{au-bu}\sin (u),(e^{bu-au}-e^{bu})\cos (u)+\sin (u)(e^{bu}-\cos (u)), \\&\cos (u)(e^{bu}-\cos (u))-(e^{bu-au}-e^{bu})\sin (u),u,v,w); u, v, w \in \mathbb R\}, \end{aligned}$$

$a\ne 0$, $b\ge 0$. Appropriate $K_{5,\epsilon }$-connected left transversals, $\epsilon =0,1$, in $G_5^c$ are: for $c=1$ the sets

$$\begin{aligned}&A_{5,1}=\{g(u,1-e^{-v},u,ve^{v}-u,v,w); u, v, w \in \mathbb R\}, \\&B_{5,1}=\{g(k,e^{-l}-1,k,-le^{l}-k,l,m); k, l, m \in \mathbb R\}, \end{aligned}$$

for $c\ne 1$ the sets

$$\begin{aligned}&A_{5,2}=\{g(u,e^{-v}-e^{-cv}, -ve^v,ve^{cv},v,w); u, v, w \in \mathbb R\}, \\&B_{5,2}=\{g(k,e^{-cl}-e^{-l},le^{l},-le^{cl},l,m); k, l, m \in \mathbb R\}. \end{aligned}$$

Appropriate $K_{6,\epsilon }$-connected left transversals in $G_6$, where $\epsilon =0,1$, are the sets

$$\begin{aligned}&A_6=\{g(u,1-v^{2}-e^{-v},-v,\frac{1}{2}v^{2}e^{v},v,w); u,v,w \in \mathbb R\}, \\&B_6=\{g(k,l+\frac{1}{2}l^{2}-le^{-l},1-e^{-l},-le^{l},l,m); k,l,m \in \mathbb R\}. \end{aligned}$$

Appropriate $K_{7,1}^{\epsilon }$-connected left transversals in $G_{7}^{p\ne 0}$, $\epsilon =0,1$, are the sets

$$\begin{aligned}&A_{7,1}=B_{7,1}=\{g(u,e^{-pv}\sin (v), \\&\frac{1}{a_{3}^{2}+1}(e^{pv}v(\sin (v)+a_3 \cos (v))+(e^{pv}- \cos (v))(\cos (v)-a_3 \sin (v))),\\&\frac{1}{a_{3}^{2}+1}(e^{pv}v(a_3 \sin (v)- \cos (v))+(e^{pv}- \cos (v))(a_3 \cos (v)+ \sin (v))),\\&v,w); u, v, w \in \mathbb R\}, a_3\in \mathbb R. \end{aligned}$$

Appropriate $K_{7,2}^{\epsilon }$-connected left transversals in $G_{7}^{p\ne 0}$, where $\epsilon =0,1$, are the sets

$$\begin{aligned}&A_{7,2}=B_{7,2}=\{g(u,e^{-pv}\sin (v),e^{pv}v \cos (v)+ \sin (v)(e^{pv}- \cos (v)),\\&e^{pv}v \sin (v)-\cos (v)(e^{pv}-\cos (v)),v,w); u, v, w \in \mathbb R\}. \end{aligned}$$

Appropriate $K_{8,\epsilon }$-connected left transversals in $G_8$ with $\epsilon =0,1$ are the sets

$$\begin{aligned}&A_8=\{g(ve^{v}+v^{2},v,u,1-e^{-v},v,w); u,v,w \in \mathbb R\}, \\&B_8=\{ g(l^{2}-le^{l},l,k,e^{-l}-1,l,m); k,l,m \in \mathbb R\}. \end{aligned}$$

Hence the assertion follows from Proposition 1. $\square$

Corollary 2

Each 6-dimensional solvable decomposable Lie group which is the group Mult(L) of a 3-dimensional connected topological loop L has 1- or 2-dimensional centre and 3-dimensional commutator subgroup.

Proof

If L has 1-dimensional centre, then the assertion follows from Proposition 3. If L has 2-dimensional centre, then Proposition 6 yields the assertion. $\square$

Corollary 3

Each solvable Lie group of dimension 6 which is realized as the group Mult(L) of a 3-dimensional connected topological proper loop L has 1- or 2-dimensional centre and 2- or 3-dimensional commutator subgroup.

Proof

If L has a 6-dimensional solvable indecomposable Lie group as its multiplication group, then the assertion is proved in Corollary 3.4 in [9]. If L has a 6-dimensional solvable decomposable Lie group as its multiplication group, then Corollary 2 gives the assertion. $\square$