Source Mechanisms of Induced Earthquakes at The Geysers Geothermal Reservoir

Abstract

At The Geysers geothermal reservoir in northern California, evidence strongly suggests that activities associated with production of electric power cause an increase in the number of small earthquakes. First-degree dynamic moment tensors are used to investigate the relationship between induced earthquakes and injection of water into a well as part of a controlled experiment in the northwest Geysers. The estimation of dynamic moment tensors in the complex shallow crust at The Geysers is challenging, so the method is described in detail with particular attention given to the uncertainty in the results. For seismic events in the moment magnitude range of 0.9–2.8, spectral moduli of dynamic moment tensors are reliably recovered in the frequency range of 1–100 Hz, but uncertainty in the associated spectral phases limits their use to a few simple results. A number of different static moment tensors are investigated, with the preferred one obtained from parameters of a model fitted to the spectral modulus of the dynamic moment tensor. Moment tensors estimated for a group of 20 earthquakes exhibit a range of source mechanisms, with over half having significant isotropic parts of either positive or negative sign. Corner frequencies of the isotropic part of the moment tensor are about 40 % larger than the average of the deviatoric moment tensor. Some spatial patterns are present in source mechanisms, with earthquakes closely related in space tending to have similar mechanisms, but at the same time, some nearby earthquakes have very different mechanisms. Tensional axes of displacement in the source regions are primarily horizontal, while the pressure axes range from near horizontal to vertical. Injection of water into the well in the center of the study area clearly causes an increase in the number of earthquakes per day, but an effect upon source mechanisms is not evident.

1 Introduction

The Geysers geothermal reservoir in northern California is not only the world's largest producer of geothermal electricity but also the most thoroughly studied example of induced seismicity related to enhanced geothermal activity. Commercial production of energy from reservoir steam began in the 1960's, and since about 1970 the operators of the reservoir have been injecting water back into the reservoir. This injected water is steam condensate, local rain, stream water, and more recently has included treated wastewater from nearby communities. As is the case with most geothermal systems, this injection of water is necessary in order to maintain pressures and insure the long term economic viability of the endeavor.

The Geysers geothermal reservoir is located in the coast ranges of northern California and is contained within the broad transcurrent boundary between the North American and Pacific plates. There are several active fault systems in the region (Bufe et al. 1981) so seismic activity in the vicinity of the Geysers is common (Eberhart-Phillips and Oppenheimer 1984), but within the geothermal reservoir seismicity does not appear to be associated with any of these fault systems. Rather, hypocenters of earthquakes within the reservoir show a close association in both space in time with either the production of steam or the injection of water (Bufe et al. 1981; Ludwin et al. 1982; Eberhart-Phillips and Oppenheimer 1984; Oppenheimer 1986; Stark 1992; Romero et al. 1994). The general conclusion is that most of the seismicity at The Geysers is induced by activities associated with production of geothermal power (Majer et al. 2007).

While there seems to be general agreement that geothermal operations play a role in inducing seismic activity at The Geysers, the physical mechanisms involved in this process are still not understood. Suggested mechanisms include volumetric contraction of the reservoir caused by the withdrawal of fluid (Majer and McEvilly 1979) or thermal cooling (Denlinger et al. 1981; Stark 2003), conversion of aseismic creep to stick-slip failure (Allis 1982), and the increase in the coefficient of friction caused by precipitation of silica on fracture surfaces (Allis 1982). A more complete understanding of the cause of induced earthquakes at The Geysers could help guide the economic development of the reservoir and help alleviate concerns in surrounding communities.

An objective of the present study is to take another look at the cause of induced seismicity at The Geysers through a careful analysis of seismograms recorded by a local network. Source mechanisms of a group of earthquakes that occurred during a controlled experiment are characterized by estimating their dynamic force moment tensors. The interpretation of these moment tensors can help constrain the physical processes taking place in the source regions of the earthquakes.

2 Previous Studies

Before describing the methods and results of the present study, it is useful to briefly review some previous studies related to source processes of earthquakes and material properties of the shallow crust at The Geysers.

A number of geodetic studies have attempted to place constraints on deformation that is taking place within the shallow crust at The Geysers. The reasons for this deformation in a vapor dominated reservoir such as The Geysers are complicated and involve an interplay between several processes that accompany two-phase fluid flow in a fractured medium with both pressure and temperature variations (Pruess and Narasimhan 1982). Denlinger et al. (1981) analyzed geodetic measurements and found that the geothermal reservoir is subsiding. Lofgren (1981) and Denlinger and Bufe (1982) analyzed local geodetic data at The Geysers and found a negative strain in horizontal directions and subsidence in the vertical direction. Mossop and Segall (1997, 1999) and Segall and Fitzgerald (1998) analyzed GPS and leveling data that confirmed earlier estimates of subsidence within the reservoir, with rates as high as 0.047 ± 0.002 m/year during the period 1977–1996. They also estimated volume strain, temperature change, pressure change, and bulk modulus in the producing part of the reservoir. Prescott and Yu (1986) used regional geodetic data to show that regional strain in The Geysers was primarily a shear with extension oriented N79°W and contraction oriented N11°E. In summary, deformation at The Geysers describes a geothermal reservoir that is undergoing volumetric contraction while contained within a regional shear field.

Seismological studies at The Geysers have used a number of different approaches to infer forces and processes acting in the source regions of earthquakes. Oppenheimer (1986) performed fault plane studies using polarity of p waves for 210 seismic events at The Geysers and found below a depth of 1 km primarily horizontal extension in a WNW direction and compression ranging from horizontal to vertical along a NNE azimuth. The general conclusion was that source mechanisms were consistent with the regional strain field.

O’Connell and Johnson (1988) calculated dynamic moment tensors of three events at The Geysers and obtained results that were more robust than those based on first motion polarities. One of the events appeared to have a significant isotropic part, but the possibility that this was an artifact caused by errors in the source location or velocity model used in the inversion could not be ruled out.

Kirkpatrick et al. (1996) obtained static moment tensors for 2,552 events at The Geysers, with 1,697 of the events in the northwest Geysers, the location of the present study. Amplitudes of direct p and s phases were measured and Green functions calculated with ray theory were used to solve for static moment tensors. About half of the events were predominantly double couple, but the rest contained significant isotropic and compensated linear vector dipole fractions. The isotropic parts were both positive and negative in sign with the fraction of the total moment ranging up to 0.3.

Ross et al. (1996, 1999) measured polarities of p and s waves together with p/s amplitude ratios and used linear programming methods (Julian 1986; Julian and Foulger 1995) to obtain relative static moment tensors for 30 events at The Geysers. About 70 % of the events had significant isotropic parts, both positive and negative in sign, with the isotropic fraction of the total moment being >0.2 for 50 % and >0.3 for 17 %. Orientations of the T and P axes showed considerable variation.

Guilhem et al. (2014) compared static moment tensor solutions obtained with a short-period local network at The Geysers with those obtained with a long-period regional network and found generally consistent results for 14 events. A time-domain method (Dreger 2003) was used to obtain static moment tensors for two different frequency bands and these were compared with first-motion solutions. Decompositions of the moment tensors varied somewhat between the different solutions, but on the average the events were about half double couple, the isotropic fraction ranging between 0 and 0.3, and the remaining fraction was compensated linear vector dipole.

Extracting source information from seismic waveform data requires the calculation of elastic wave propagation effects and, this in turn, requires knowledge about the velocity structure. Considerable information of this type is available, and all of it indicates that the upper crust at The Geysers is highly heterogeneous. This begins with the topography, as the terrain is rugged and mountainous with elevations ranging from <500 m to over 1,400 m. Because of the steep terrain, there are numerous landslides. The geology is equally complex, with the Franciscan subduction complex broken into a series of fault-bounded slabs that are intruded by a silicic batholith (Thompson 1992). The geothermal reservoir is highly fractured with the orientation of the fractures generally random (Thompson and Gunderson 1992; Beall and Box 1992). The general reservoir model has high-angle fractures of varying strike separating the sedimentary section into blocks that contain low-angle fractures of limited extent, while the intrusive section is dominated by high-angle fractures.

O’Connell and Johnson (1991) developed a one-dimensional velocity model for The Geysers through a process of progressive inversion for p velocity, s velocity, and hypocenters. Particular attention was given to the compressional velocity to shear velocity ratio v _p /v _s that shows considerable variation with depth and a minimum that correlates with the zone of maximum steam production. Boitnott (1995) used laboratory measurements on rocks from The Geysers and the Biot-Gassmann poroelastic theory to show that the variations in v _p /v _s are consistent with changes in the degree of saturation. Romero et al. (1994) also used a progressive inversion procedure to solve the three-dimensional problem for hypocenters, p velocity, v _p /v _s velocity ratio, and a differential quality factor for p waves Q _p . The three-dimensional variations in velocity and attenuation appeared to correlate with the geology.

Zucca et al. (1994) used measurements of arrival times and pulse widths to calculate a three-dimensional model for compressional velocity v _p and a one-dimensional model for compressional attenuation Q _p down to a depth of 1.5 km below sea level. The shallow part of the v _p model correlated with surface geology, and, at depth, low values of v _p correlated with parts of the reservoir where there had been production of steam and reduction in pressure. The Q _p values are low near the surface, increase with depth, and then decrease within the zone of steam production.

Julian et al. (1996) used arrival times of direct compressional and shear waves to calculate three-dimensional models of v _p and the ratio v _p /v _s from the surface down to a depth of 3 km below sea level. The lateral variation in v _p was ±12 % of mean values and the pattern was in general agreement with that of Zucca et al. (1994). The most notable feature of the v _p /v _s results was a strong −9 % anomaly that correlated with the most intensively exploited part of the geothermal reservoir.

Romero et al. (1997) used a spectral ratio method to estimate three-dimensional variations in differential attenuation for both p and s waves in the northwest Geysers. The differential attenuation showed significant lateral variations, particularly near the surface where it was correlated with mapped geologic units. A zone of high p wave attenuation and low v _p /v _s appeared to delineate the geothermal reservoir.

Majer et al. (1988) used vertical seismic profiling to study anisotropy in the upper 1.5 km of The Geysers reservoir. They found no evidence for anisotropy in p waves, but sv waves had about 11 % higher velocities than sh waves. They concluded that this was consistent with effects of known fracture geometry. Evans et al. (1995) used shear-wave splitting to study seismic anisotropy at The Geysers and found a complex pattern. If the anisotropy is confined to the upper 1.5 km of the crust, it averages 4 %. Elkibbi et al. (2005) and Elkibbi and Rial (2005) used shear-wave splitting to study anisotropy in both the northwest and southeast Geysers and also found the average anisotropy in shear wave velocities to be about 4 %. They concluded that the results in the northwest Geysers could be explained by systems of vertical extensional cracks aligned parallel to the direction of principal horizontal compressive stress (N to NE). In the southeast Geysers the fast shear wave polarizations showed more variation and suggested that more than one system of fractures might be present.

The possibility that material properties at The Geysers may be changing with time because of production activities must also be considered. Foulger et al. (1997) found that between 1991 and 1994 the v _p /v _s ratio in the center of the reservoir decreased by 4 % and attributed this to a change in v _p caused by a conversion of pore water to steam.

The picture that emerges from this consideration of previous studies at The Geysers is one of a fairly complicated shallow crust. There are strong lateral variations in topography and geology at the surface that cause similar variations in elastic velocities. These lateral variations in elastic velocities extend to a depth where they correlate with lithology as well as steam production activities. There is also evidence for significant vertical and lateral variations in the attenuation and anisotropy of elastic waves. Superimposed on this heterogenous crustal structure is a deformation field that involves volumetric contraction within a regional shear field. Earthquakes at The Geysers are more complicated than most tectonic earthquakes, as they contain significant isotropic parts and are related to steam production activities. The situation is further complicated by the likelihood that both material properties and earthquake mechanisms are functions of time.

3 Data

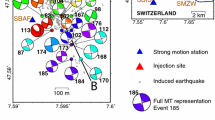
The seismic data used in this study are selected to take advantage of a recent controlled experiment that is investigating the relationship between seismicity and the injection of water. The Northwest Geysers Enhanced Geothermal System Demonstration Project began in 2010 as a test of the feasibility of stimulating a deep high-temperature reservoir (Rutqvist et al. 2010; Garcia et al. 2012). The project is located in an undeveloped part of the reservoir where two previously abandoned wells, Prati 32 (P32) and Prati State 31 (PS31), were prepared for use as an injection and production well pair. P32 was completed to a depth of 2,672 m below sea level (bsl). The injection interval in P32 is between 1,653 and 2,672 m bsl. A square study area centered on P32 with dimensions of 1.5 km is the site selected for this study. Only earthquakes with epicenters within this study are used. Figure 1 is a map showing the location of this study area within The Geysers geothermal reservoir along with the locations of the seismographic stations that are used.

Fig. 1

Map of The Geysers geothermal reservoir with the dashed line showing the approximate boundary of the steam production zone. The small circles are locations of stations of the LBNL seismic monitoring network that are used in this study. The rectangle in the northwest part of the reservoir is the study area that contains the epicenters of all events used in this study

The observational data for this study are the seismograms produced by the LBNL seismic monitoring network at The Geysers. This network consists of three-component digital stations that are mostly within the production boundaries at the Geysers (Major and Peterson 2007). The seismometers have a response that is flat to ground velocities at frequencies above 4.5 Hz. The seismometer outputs are continuously digitized with a resolution of 24 bits and a sample rate of 500 samples per second. The data are routinely processed to identify seismic events along with their hypocenters and magnitudes with a lower threshold for complete coverage at the Geysers of about magnitude one. Locations of the LBNL seismographic stations used in this study are shown in Fig. 1. All of the stations used in this study are located at the free surface.

As part of the EGS Demonstration Project, injection of water into P32 began on October 6, 2011 (Garcia 2012). An initial rate of 1,100–1,200 gallons per minute (gpm) was used to collapse the steam bubble in the well bore and continued for 12 h. The rate was then reduced to 400 gpm and maintained for 54 days. On 29 November, 2011, the injection rate was increased to 1,000 gpm, on 7 March, 2012, it was reduced to 700 gpm, and on 11 June 2012, it was reduced to 400 gpm. This injection rate is plotted in Fig. 2. Note that water is simply poured into the well with no pressure applied other than the force of gravity.

Fig. 2

Number of earthquakes per day with M _w ≥ 0 and epicenters in the study area shown in Fig. 1. Time is measured in days from the beginning of injection on 6 October 2011. The dashed line is the rate of injection of water into P32. The symbols at the top denote origin times of events in Table 1

The frequency of earthquakes that have epicenters in the study area around P32 for a time interval of 600 days is shown in Fig. 2. In the 300 days before injection began, there are 241 events in the magnitude range 0.4 ≤ M ≤ 1.9, while in the 300 days after injection began there are 2,107 events in the magnitude range 0.0 ≤ M ≤ 2.8. Figure 2 shows that there is a clear correlation between the rate of seismicity near P32 and the rate of water injection into that well. Prior to the beginning of injection, the rate of seismicity has a low background value of about 1–2 events per day, but this jumps to a much higher value when injection begins. Abrupt increases in injection rate cause abrupt increases in seismicity.

From the earthquakes shown in Fig. 2, a group of 20 are selected for moment tensor inversion, with the times of these events marked at the top of the figure. The selection criteria are designed to provide a broad range in event times, depths, and magnitudes. The group includes five events spread out over the time interval before injection in P32 began and 15 events that sampled all of the time intervals of different injection rate shown in Fig. 2. Depths of the selected events ranged between about 2.0 and 3.0 km below sea level. Magnitudes ranged between 0.9 and 2.8, with the lower limit set by the requirement of a good signal to noise ratio on the seismograms and the upper limit equal to the largest event in the time interval considered. The group of selected events is listed in Table 1.

Table 1 Origin times, hypocenters, and magnitudes of events selected for moment tensor inversion

Hypocenters of the 20 events selected for moment tensor inversion are plotted in the map of Fig. 3 and cross sections in Figs. 4 and 5. These figures show the proximity of the events to the P32 well. All events are within 720 m horizontal distance of P32 or the downward projection of its bottom. Events with numbers 1–5 occurred before injection into P32 began, and they are at approximately the same depth with their epicenters roughly aligned in a NNE direction. Events with numbers 6–20 occurred while injection into P32 was taking place and their hypocenters show significant clustering about the well for many but not all of the events.

Fig. 3

Map of epicenters of events selected for moment tensor inversion. Numbers correspond to the event numbers in Table 1. The line is the surface projection of the P32 well with the label at the well head

Fig. 4

Cross section from west to east through the center of the map in Fig. 3. Z is depth below sea level

The events listed in Table 1 are analyzed with data recorded at the stations shown in Fig. 1. More stations than those shown in Fig. 1 are available, but stations at epicentral distances greater than about two source depths are not used because the seismograms at these distances are dominated by surface waves that are difficult to model with Green functions. The strong three-dimensional heterogeneity in topography and material properties near the surface at The Geysers is likely to cause strong scattering and multi-pathing of surface waves. Although data from all of the stations shown in Fig. 1 are not available for all of the events listed in Table 1, data from a minimum of ten stations are available for each event. Only stations with three operating components are used, so at least 30 components of data are used in each moment tensor inversion.

4 Moment Tensor Method

The basic procedure followed in this study is to characterize an earthquake by its first-degree dynamic moment tensor, which is a general and fairly complete mathematical representation of an earthquake source. The general idea is that effects of wave propagation through the earth that are present in the observational data will be removed in the process of estimating the moment tensor. While this ideal can not be completely realized in a complicated region such as The Geysers, properties of the source process are much more clearly displayed in the moment tensor than in the original seismograms.

Consider the situation where K different seismogram components are available and let the k component that is recorded at location x and time t be denoted by v _k (x, t). This component is sampled in time with a sampling interval $\Updelta t$ and a data window is selected beginning before the arrival of the first p wave, continuing to a couple of seconds after the arrival of the direct s wave, and having a total of N samples. A discrete Fourier transform is performed on this data window to obtain V _k (x, f), where upper case letters are used to denote functions in the frequency domain. The presence of random noise in the data is taken into account by calculating the variance of each component var[v _k (x, t)] from an interval of time immediately before the arrival of the direct p wave. It is assumed that the noise is stationary, uncorrelated between components, and independent of frequency. Then, using Parseval's formula, the variance of the data in the frequency domain is

$$ {\rm {var}}[V_k({\bf x},\,f)] = N (\Updelta t)^2 {\rm {var}}[v_k({\bf x},t)]. $$

(1)

The method of estimating the moment tensor in this study follows that of Stump and Johnson (1977). It is assumed that the earthquake source process can be adequately represented by the symmetric first-degree moment tensor m _ij (t), which is equivalent to assuming that the wavelengths of interest are large compared to the dimensions of the source volume. This assumption is reasonable at frequencies up to about the corner frequency of the source spectrum (Stump and Johnson 1982), but caution must be exercised in the interpretation of frequencies beyond this point. Given this assumption, the k seismogram component can be represented

$$ v_k({\bf x},t) = r(t)^{\odot} g_{ki,j}({\bf x},t;{\bf 0},0)^{\odot} m_{ij}(t), $$

(2)

where r(t) is the instrument response function of the seismograph, g _ki,j is the j spatial derivative of the Green function, and m _ij (t) is the dynamic force moment tensor. Here the symbol $^{\odot}$ represents convolution in time, and it is assumed that the source process is centered at the origin of the coordinate system and starts at time t = 0. In this and later equations a repeated index in a product of terms implies summation from 1 to 3. Because m _ij (t) is a symmetric second-rank tensor, it has six independent values at each instant of time.

The seismogram in the frequency domain is

$$ V_k({\bf x},\,f) = R(f) \, G_{ki,j}({\bf x},\,f;{\bf 0},0) \, M_{ij}(f). $$

(3a)

Such an equation can be written for every seismogram component that is observed, with only the Green function changing as the component and location of the seismogram changes. Thus, if K different seismogram components are available, at every frequency there is a system of K linear equations that can be solved for the six independent unknown values of M _ij (f). The dynamic moment tensor m _ij (t) will generally contain a static offset so its Fourier transform M _ij (f) will diverge as f ⁻¹ at low frequencies. Thus, the numerical stability of the solution is improved by considering the alternative system

$$ V_k({\bf x},\,f) = \frac{R(f)}{i2\pi f} \, G_{ki,j}({\bf x},\,f;{\bf 0},0) \, \dot{M}_{ij}(f), $$

(3b)

where $\dot{M}_{ij}(f)$ and its inverse Fourier transform $\dot{m}_{ij}(t)$ is the dynamic moment rate tensor. The statistical reliability of the problem can be improved by weighting the data with the inverse standard deviation of the noise, and, in that case, the system becomes

$$ \frac{V_k({\bf x},\,f)}{\sqrt{{\rm {var}}[V_k({\bf x},\,f)}]} = \frac{R(f)}{i2\pi f} \, \frac{ G_{ki,j}({\bf x},\,f;{\bf 0},0)}{\sqrt{{\rm {var}}[V_k({\bf x},\,f)]}} \, \dot{M}_{ij}(f). $$

(3c)

With K components of data available for analysis, at any given frequency value f the Fourier transform values (with possible weighting) can be collected to form a column matrix $\mathcal{V}(f)$ with dimensions K by 1. For each component, there are six Green functions corresponding to the six independent terms of the moment tensor and these are treated similarly to the data to form a matrix $\mathcal{G}(f)$ that has dimensions K by 6, where the instrument response and possible weighting are included with the Green function. The unknown six independent terms of the moment rate tensor form the column matrix $\dot{\mathcal{M}}(f)$ with dimensions 6 by 1. Thus, for each frequency any of Eqs. 3a and b, or c can be written as the linear matrix equation

$$ {\mathcal{V}}(f) = {\mathcal{G}}(f) \, \dot{{\mathcal{M}}}(f). $$

(4)

This is a linear inverse problem, and the solution can be written formally as

$$ \dot{{\mathcal{M}}}(f) = {\mathcal{G}}^{-1}(f) \, {\mathcal{V}}(f). $$

(5)

The variance of the solution is

$$ {\rm {var}}[\dot{{\mathcal{M}}}(f)] = ({\mathcal{G}}^{-1}(f))^2 \, {\rm {var}}[{\mathcal{V}}(f)]. $$

(6)

Following Stump and Johnson (1977), it is convenient to obtain the solution to this inverse problem using singular value decomposition (Lanczos 1961).

The approach outlined in the preceding paragraphs produces estimates of $\dot{M}_{ij}(f)$ and ${\rm {var}}[\dot{M}_{ij}(f)].$ An inverse Fourier transform leads to $\dot{m}_{ij}(t)$ and a numerical integration then leads to the dynamic moment tensor m _ij (t). As the first step in the interpretation of the moment tensor, it is convenient to decompose it into its eigenvalues and eigenvectors. Because the moment tensor is symmetric, the eigenvalues are real and can be denoted

$$ \Uplambda_T (t) \ge \Uplambda_I (t) \ge \Uplambda_P (t). $$

(7)

The corresponding unit eigenvectors are

$$ \hat{\bf e}^T (t), \hat{\bf e}^I (t), \hat{\bf e}^P (t). $$

(8)

The directions of the eigenvectors are referred to as the T, I, and P axes and interpreted as principal directions of displacement in the source region.

The trace of the moment tensor is an invariant that is related to the isotropic part of the moment tensor by

$$ m_{\rm {iso}}(t) = \frac{1}{3} \Big[ \Uplambda_T (t) + \Uplambda_I (t) + \Uplambda_P (t) \Big] = \frac{1}{3} \Big[ m_{11}(t) + m_{22}(t) + m_{33}(t) \Big] $$

(9)

and identified with volume change in the source process. The deviatoric moment tensor is defined as

$$ m_{ij}'(t) = m_{ij}(t) - m_{\rm{iso}}(t) \delta_{ij}. $$

(10)

The static moment tensor is defined as

$$ \tilde{m}_{ij} = m_{ij}(t \rightarrow \infty ) = \dot{M}_{ij}(f \rightarrow 0) $$

(11)

and is equivalent to a dynamic moment tensor with all elements having the same time dependence of a unit step function. In practice, the static moment tensor is often estimated at a time other than infinity or a frequency other than zero, so a variety of different results are possible for the same event. It is also possible to assume that all elements of the moment tensor have the same functional time dependence that is different from a step function and include the estimation of this function in the process of estimating the static moment tensor. This static moment tensor can also be decomposed into eigenvalues and eigenvectors that are no longer a function of time or frequency.

The scalar moment m _o is defined as the norm of the static moment tensor, which is here taken to be the Euclidean norm and equal to the maximum of the absolute values of the eigenvalues (Franklin 1968).

$$ m_o = {\rm {max}} \Big\{ |\tilde{\Uplambda}_T|, \, |\tilde{\Uplambda}_I|, \, |\tilde{\Uplambda_P}| \Big\}. $$

(12)

Bowers and Hudson (1999) discuss alternative definitions of the scalar moment. The moment magnitude is given by

$$ M_w = \frac{2}{3} \log_{10}(m_o), $$

(13)

where m _o is given in units of GNm. All moments in this study are given in units of GNm.

The velocity model used in calculating Green functions plays a critical role in the estimation of the moment tensor. The complicated shallow crust at The Geysers presents a problem in this respect because of the difficulty of calculating accurate and complete Green functions in the frequency range 0–250 Hz for a model that is heterogeneous in three dimensions. The choice made in the present study is to use a one-dimensional model that allows straightforward Green function calculations and then make adjustments to approximate some of the three-dimensional effects. The chosen base model is a layered model that was developed by O’Connell and Johnson (1991) for The Geysers region, and it is shown in Fig. 6.

Fig. 5

Cross section from south to north through the center of the map in Fig. 3. Z is depth below sea level

Fig. 6

Compressional velocity (solid line) and shear velocity (short dash line), both in units of m/s, and density (long dash line) in units of kg/m³

The model shown in Fig. 6 is a base model that is modified to make it more appropriate for the individual seismic stations. This model has two layers above sea level, with the upper layer having a thickness of 200 m and the second layer having a nominal thickness of 1,000 m, so the surface elevation has a nominal value of 1,200 m. There is considerable topography at The Geysers, with the elevation of the seismic stations shown in Fig. 1 ranging between 327 and 1,112 m above sea level. To accommodate this range in elevation, the model is adjusted to have the correct elevation at each station by adjusting the thickness of the second layer. The compressional and shear velocity of the second layer are also adjusted at each station so as to minimize travel time residuals that result when origin times and hypocenters of the seismic events are determined. Thus, a different model is used for each seismic station with the differences between stations confined to the two layers above sea level. Velocities above sea level range between 1,800 and 3,300 m/s for p waves and between 1,400 and 2,060 m/s for s waves. These near surface adjustments achieve the same effect as commonly used station correction terms, but have the advantage of correctly including elevation and slowness effects.

Attenuation is included in the model by assuming quality factors of Q _p  = Q _s  = 100 above sea level and Q _p  = Q _s  = 200 below sea level. These values are chosen to be somewhat larger than the one-dimensional estimates of Zucca et al. (1994) and Romero et al. (1997) in order to avoid a problem caused by the lateral variations in attenuation at The Geysers. As pointed out by Romero et al. (1997), there are significant differences in the frequency content of the same seismic phase observed at different stations. Thus, if Green functions are calculated with average attenuation values, the energy from seismic stations with enriched frequency content will contaminate the moment tensor estimates at high frequencies. Part of this problem may relate to the possibility that much of the observed attenuation may be caused by scattering, while the Green functions are calculated assuming it is caused by intrinsic attenuation.

The Green functions are calculated for a one-dimensional layered model using the invariant embedding method of Kennett (1974) and Kennett and Kerry (1979). The dispersion associated with attenuation is included with the constant Q formulation of Kjartasson (1979).

5 Dynamic Moment Tensor Results

In this study the data sample interval is $\Updelta t = 2$ m s and the data window has N = 2,048 sample points for a total duration of 4.1 s, with the first p wave arriving at least 0.5 s after the beginning of the window. The Nyquist frequency is f _N  = 250 Hz. A time window of 0.4 s duration before the arrival of the p wave is used to estimate the noise level var[v _k (x, t)]. A cosine taper is applied to the second half of the time window to bring the amplitude smoothly to zero at the end.

The events shown in Fig. 2 are located with a three-dimensional model using arrival times of p waves and s waves (Ernie Majer, personal communication, 2012). However, the model used in the moment tensor inversion process is one-dimensional. Thus, new origin times and hypocenter locations are determined for each event in Table 1 using the model of Fig. 6 and employing travel times of both p and s waves. Differences between the original and relocated hypocenters are small, generally <100 m, but this step helps improve compatibility between the observational data and the Green functions. The standard errors of the travel time residuals are always <0.02 s and the estimated uncertainty in relocated hypocenters is about 50 m in the horizontal direction and 100 m in the vertical direction.

The basic procedure used in estimating dynamic moment tensors along with some of the problems that are encountered in the process are best illustrated by showing some of the intermediate results for one of the events. Figure 7 shows observational data at one station for event 12 of Table 1. Also shown for comparison are data calculated with a static moment tensor from Table 2 that is combined with the Green function and instrument response. It is assumed in this case that all elements of the moment tensor have the same time function, which in this case is a simple pulse with a corner frequency of 10 Hz and high-frequency asymptote power of 3. The observed data have portions of time with significantly larger amplitudes than the calculated data, such as the time before the arrival of the s wave on the T component and the time beginning about 0.5 s after the s wave on all three components. This lack of agreement raises a critical question that impacts several aspects of this study. Namely, are these unmodeled parts of the observed data caused by the time functions of the dynamic moment tensor or are they artifacts due to inaccuracies in the Green functions?

Fig. 7

Observed seismograms in the radial (R), transverse (T), and vertical (Z) direction at station AL1 at an epicentral distance of 3.67 km and azimuth of 275° from event 12. The 2nd, 4th, and 6th traces are calculated seismograms that result when a static moment tensor is combined with the Green function, source pulse, and instrument response. The numbers on the right are maximum amplitudes in digital counts. The zero time is 0.67 s after the origin time of the event. The dashed vertical lines show the arrival times of direct p and s waves calculated with ray theory

Table 2 Parameters of the dynamic moment rate spectral moduli for event 12

As described in the previous section, the dynamic moment tensor is obtained as the solution to a linear inverse problem that produces the Fourier transform of the moment rate function $\dot{\mathcal{M}}(f)$ (Eq. 5). The spectral modulus of that solution is displayed for the six independent elements of the moment rate function in Fig. 8. Also shown in Fig. 8 is the uncertainty in the modulus of the moment rate tensor from Eq. 6. Over most of the frequency range, the spectral modulus is much larger than its uncertainty and, thus, well determined, but this not true at both the lowest and highest frequency ranges. At frequencies above 100 Hz, the spectral modulus is basically noise. This is caused by the fact that the source time functions of the moment tensor elements all have corner frequencies in the range of 10–20 Hz and at higher frequencies the amplitude falls off rapidly until the noise level is reached at about 100 Hz. This aspect of the solution is not much of a problem because, if desired, the frequencies above 100 Hz could be removed by filtering without affecting any of the lower frequencies.

Fig. 8

Spectral moduli of the moment rate tensor $| \dot{M}_{ij}(f)|$ for event 12. The index ij is shown in the upper right of each panel. The solid line is the estimated modulus, the long dash line is an estimate of its uncertainty, and the short dash line is a model fitted to the modulus

The fact that the spectral modulus of the moment rate tensor elements begins to approach its uncertainty at frequencies <1 Hz is a more serious problem. The most likely cause of this problem is the instrument response that has a corner frequency at 4.5 Hz and a fall-off power of −3 below that so the lowest frequencies are weakly recorded in the data. Also note that uncertainties shown in Fig. 8 are calculated assuming the noise spectrum is independent of frequency, so if this is not true and the noise is enriched in low frequencies, then the situation is even worse than shown in Fig. 8. Because of this problem at low frequencies, features of the dynamic moment tensors at frequencies <1 Hz are regarded as having considerable uncertainty and used only when necessary. Their use can not be completely avoided because moment rate tensors in the time domain must be integrated to obtain moment tensors and low frequencies play an essential role in this integration process.

In analyzing spectral moduli of the moment rate tensors such as those shown in Fig. 8, it is useful to parameterize the primary features of the spectrum. A model (Ihaka 1985) is fitted to the spectral modulus of each moment rate tensor element that has the form

$$ |\dot{M}_{ij}(f)| = \frac{\tilde{m}_{ij}}{ 1 + \left(\frac{f}{f_{\rm {c}}}\right)^{s_{\rm {h}}} } + \overline{n}. $$

(14)

This model is fitted to the spectral modulus in the frequency interval between 1 and 100 Hz, with lower and higher frequencies not included because of the noise problems discussed earlier. The short dash lines in Fig. 8 are this model fitted to the spectral moduli and plotted over the entire frequency range.

In this spectral model the low frequency level of the spectral modulus is interpreted as an estimate of the static moment tensor $\tilde{m}_{ij}$ (Eq. 11). The parameter f _c is an estimate of the corner frequency of the source time function with s _h an estimate of the power of the high frequency asymptote. The parameter $\overline{n}$ is an estimate of the average random noise level in the spectral domain and generally has a small value that has not proved to be useful. The estimate of the static moment tensor $\tilde{m}_{ij}$ is essentially a measure of the level of the spectral modulus of the moment rate tensor in the frequency interval between 1 Hz and the corner frequency f _c that is typically in the range 10–20 Hz. Accordingly, an estimate of the uncertainty of this static moment tensor element is the root-mean-square value of the difference between the observed and fitted spectral estimates in this same frequency interval. Here, and throughout this paper, the uncertainty of an estimate is termed the standard deviation and labeled sd[estimate]. Also used is the coefficient of variation that is defined as cv[estimate] = sd[estimate]/|estimate|. When this fitting process is applied to the six independent elements of the dynamic moment rate spectral modulus (Fig. 8) for event 12 of Table 1, the results listed in Table 2 are obtained.

A notable feature of Table 2 is the fact that the corner frequency f _c is considerably larger on the diagonal elements than on the off-diagonal elements of the moment tensor. To determine whether the isotropic part of the moment tensor is causing this effect, the fitting process is applied to the deviatoric (Eq. 10) and isotropic (Eq. 9) parts of the moment rate tensor and the results are listed in Table 3. This table clearly shows that the corner frequency of the deviatoric moment tensor is significantly less than that of the isotropic part. Averaging the six elements of the deviatoric moment tensor gives $\overline{f}_{\rm {{cd}}} = 7.7 \pm 0.9$ Hz, whereas for the isotropic part. f _ci = 13.3 Hz. The high-frequency power is also smaller for the deviatoric part and has the average $\overline{s}_{\rm {{hd}}} = 2.9 \pm 0.1$ compared to s _hi = 3.5 for the isotropic part. The coefficient of variation for the static moment is somewhat less in Table 3 than in Table 2, indicating that the spectral modulus of the deviatoric moment tensor is a slightly better fit than the complete moment tensor. These results show that for this event the isotropic part of the moment tensor is enriched in high frequencies with respect to the deviatoric moment tensor.

Table 3 Parameters of the deviatoric and isotropic dynamic moment rate spectral moduli of event 12

The spectral moduli of the dynamic moment rate tensor shown in Fig. 8 are only half of the solution. The spectral phase is also available but not shown, as it is difficult to display or parameterize the phase in a meaningful way. However, the spectral phase plays a critical role in determining the appearance of the seismograms in the time domain.

When the spectral moduli of Fig. 8 are combined with the associated spectral phase and transformed to the time domain, the dynamic moment rate functions of Fig. 9 are obtained. Although there is some acausal signal before t = 0, a prominent pulse begins at about this time on all elements of the moment rate tensor. The shape of this first pulse, which lasts for about 0.1 s, is quite similar on all six elements of the moment rate tensor, but this similarity degrades at larger times. The diagonal elements show an increase in similarity beginning at about 1 s. The duration of significant signal is about 0.8 s on the off-diagonal elements, but about 2.4 s on the diagonal elements. These differences in signal between the diagonal and off-diagonal elements of the moment rate function add support to the differences in frequency content found in Tables 2 and 3 and the idea that the deviatoric and isotropic moment tensors are significantly different.

Fig. 9

The dynamic moment rate tensor $\dot{m}_{ij}(t)$ that is obtained as inverse Fourier transforms of the spectral moduli in Fig. 8 along with the associated spectral phases. The numbers on the right are maximum amplitudes in GNm/s

The dynamic moment rate tensor elements in Fig. 9 can be integrated to obtain the dynamic moment tensor elements in Fig. 10. This integration process is complicated by the uncertainty in the moment rate tensor at low frequencies that was discussed earlier with respect to Fig. 8. This difficulty can be mitigated somewhat by using Eq. 11 and setting the long-time level of the moment function equal to the low-frequency level of the moment rate functions as determined by $\tilde{m}_{ij}$ of Eq. 14. However, there still exists a long-time drift in some of the elements that is most likely related to the low-frequency problem. To a first approximation, the dynamic moment tensors of Fig. 10 are step functions with finite rise times. Superposed on this simple time function are oscillations that vary between the various elements, Particularly conspicuous is the similarity in the waveforms between 1 and 2.4 s on the three diagonal elements that is not shared with the off-diagonal elements.

Fig. 10

The dynamic moment tensor m _ij (t) that is obtained by integrating the moment rate tensor in Fig. 9. The numbers on the right are maximum amplitudes in GNm

The moment rate tensor of Fig. 8 can be substituted on the right hand side of Eq. 3b to obtain an estimate of the calculated spectral modulus for the three components of ground motion at station AL1 for event 12. These spectra are shown in Fig. 11 along with the observed spectra at this station corresponding to the time traces in Fig. 7. There is fairly good agreement between the observed and calculated spectral moduli in the frequency range between about 1 and 100 Hz. At frequencies <1 Hz or >100 Hz the agreement is not so good, but these are the frequency ranges where the strength of the signal is the weakest. This is consistent with the earlier discussion related to Fig. 8 where it is concluded that only frequencies between 1 and 100 Hz can be considered reliable.

Fig. 11

Spectral moduli of the observed data (solid line) and the calculated data (dashed line) for the three components of ground motion at station AL1 for event 12

Starting with the dynamic moment tensor of Fig. 10 and using Eq. 2, leads to the calculated seismograms that are shown in Fig. 12. Note that the difficulties with low frequencies that are encountered in obtaining the dynamic moment tensors of Fig. 10 are not apparent in Fig. 12 because any low frequency inaccuracies become insignificant when the instrument response is included. A comparison of Figs. 7 and 12 reveals the differences between an interpretation of the data that uses a static moment tensor and one that uses a dynamic moment tensor. The moment tensor used in the calculated traces of Fig. 7 is constructed using the $\tilde{m}_{ij}$ and average values of f _c and s _h of Table 2. Figure 12 is constructed using the dynamic moment tensors of Fig. 10. The same Green function and instrument response is used in calculating Figs. 7 and 12.

Fig. 12

Similar to Fig. 7 for the observed seismograms at station AL1 for event 12. However, in this case the 2nd, 4th, and 6th traces are the calculated seismograms that result when the dynamic moment tensor of Fig. 10 is combined with the Green function and instrument response

The degree of fit between the observed and calculated seismograms in Figs. 7 and 12 is quite different. The calculated results for the static moment tensor in Fig. 7 do a reasonably good job of fitting the direct p wave on the radial and vertical components and the direct s wave on the transverse component, but essentially ignore all other parts of the observed seismograms. The calculated results for the dynamic moment tensor in Fig. 12 also do a reasonably good job of fitting the direct p wave on the radial and vertical components and the direct s wave on the transverse component, but in addition they do a much better job of fitting the general pattern of amplitude versus time on the seismograms over the entire time interval. However, a close inspection of the phase of the motion at any specific time reveals a rather poor fit for much of the seismograms.

The comparison between observed and calculated results in Figs. 7, 11 and 12 suggests an interpretation of the reliability of the dynamic moment tensor results. First, note that the calculated seismograms in Figs. 7 and 12 are based on moment tensors that have essentially the same spectral moduli of Fig. 8, the latter being the estimated values and the former being a model fitted to the estimated values. Furthermore, Fig. 11 shows that the spectral moduli of the observed seismograms are explained quite well by the calculated results in the frequency range of 1–100 Hz. Thus, the difference between the calculated seismograms in Figs. 7 and 12 and the fact that neither does a good job of fitting all of the observed data must be attributed to the role of the spectral phase. It appears that the spectral moduli of the moment tensor are fairly well determined, but the associated spectral phases contain considerable uncertainty. The sources of uncertainty in the moment tensor inverse problem, such as the noise in the data, the errors in the source location, and the inaccuracies in the Green functions, can all be regarded as noise that gets transformed primarily into the spectral phase of the solution. This interpretation is consistent with the description of random data that have a deterministic power spectral density function with all of the randomness contained in the associated phase function (Bendat and Piersol 1971). This line of reasoning leads to the conclusion that in this study the spectral moduli of the dynamic moment rate tensors are reliably determined in the frequency range between 1 and 100 Hz, but the same claim cannot be made for the spectral phases.

These questions about the reliability of the spectral phases of the dynamic moment rate tensor lead to somewhat of a quandary when it comes to interpreting the dynamic moment tensor in Fig. 10. Some of the temporal features in the tensor elements may be real properties of the source and some may just be artifacts, but it is difficult to reliably determine which is the proper interpretation of any particular feature. The fit to the direct p wave on the R and Z components and direct s wave on the T component in Fig. 12 suggests that the initial 0.1 s of the dynamic moment tensor may be a reasonably well resolved feature. The long time level of the dynamic moment rate tensor, which is based on the low frequency spectral level of the moment rate tensor, is also well resolved. However, in the intervening interval the moment tensor elements show considerable oscillation and the reliability of these features is highly suspect.

6 Static Moment Tensor Results

While the dynamic moment tensor gives the most complete representation of the source process with the fewest number of assumptions, there are situations where a less complete description may be sufficient. A static moment tensor can serve this purpose. As pointed out where the static moment tensor is defined in Eq. 11, there are a number of different methods of calculating the static moment tensor. In the present study this is a useful property because a comparison between different types of static moment tensors, and a comparison with the dynamic moment tensor provides a check on the validity of all the results.

One method of obtaining a static moment tensor is to replace the complete seismogram with the measured amplitudes of a few particular phases such as direct p or s waves. This approach is described and tested with synthetic data in Stump and Johnson (1977). Kirkpatrick et al. (1996) used this method to obtain static moment tensors for a large number earthquakes at The Geysers by measuring the amplitudes of p and s wave pulses, correcting for the instrument response, and then using ray theory to calculate Green functions. That method is also used in the present study with one modification. Instead of using ray theory for the Green functions, the full wave theory Green functions used in obtaining the dynamic moment tensors are calculated and passed through the instrument to produce synthetic seismograms on which the amplitudes of p and s wave pulses are measured. When static moment tensors obtained using the original method of Kirkpatrick et al. (1996) are compared with those obtained with the modified method of this study, the results are almost identical in most cases, but in cases where they differ, the modified approach gives the most consistent results. The wave theory basis of the modified approach has some advantages over the original approach in the manner that near-field terms and the instrument correction are handled. When this modified approach is applied to the data of event 12 of Table 1 the first two types of static moment tensors listed in Table 4 are obtained. The first type uses only the amplitudes of p waves measured on vertical component seismograms, while the second type uses both the amplitudes of p waves on vertical component seismograms and the amplitudes of s waves on transverse component seismograms. Other combinations of phases and components could also be used. Solutions for these types of static moment tensors are straightforward least squares estimates so standard errors of the estimates are available, and these uncertainties are also listed in Table 4.

Table 4 Different types of static moment tensors for event 12

It is also possible to extract static moment tensors from the dynamic moment tensor. O’Connell and Johnson (1988) first calculated dynamic moment tensors for three events at The Geysers and then averaged these results over a time interval of 0.5 s to obtain an estimate of the static moment tensor. The same method is used in this study and the dynamic moment tensors of Fig. 10 are averaged over the time interval 0–0.1 s to arrive at the estimates that are listed as type 3 in Table 4. The standard error of the mean is also listed as an estimate of the uncertainty. With this type of static moment tensor the results depend upon the time interval that is selected for averaging, which follows from the fact that the six independent elements of the dynamic moment tensor shown in Fig. 10 do not have identical time functions.

Another method of obtaining a static moment tensor from the dynamic moment tensor is to use the parameter $\tilde{m}_{ij}$ of the spectral model given in Eq. 14. This type of estimate and its uncertainty are already listed in Table 2. This is basically an estimate of the level of the spectral modulus at low frequencies, and in this study that turns out to be the frequency interval between 1 Hz and the corner frequency f _c. The static moment tensor of this type is listed as type 4 in Table 4.

A common method of displaying the information contained in a static moment tensor is to calculate the eigenvalues (Eq. 7) and eigenvectors (Eq. 8) and then plot the T, I, and P axes on a stereographic projection of the focal sphere. This is done in Fig. 13 for the four different types of static moment tensors listed in Table 4. The basic information contained in these plots is the points where the T, I, and P axes pierce the lower half of the focal sphere. The solid lines on the plots are the intersection with the focal sphere of the planes orthogonal to the T and P axes. In addition, the stippled areas on the plots show the areas where P waves emerging from the source have a polarity away from the source, which corresponds to upward motion on a vertical component seismogram.

Fig. 13

Equal area stereographic projections of the principal axes of the four different types of static moment tensors listed in Table 4, with a corresponding to type 1, b to type 2, c to type 3, and d to type 4. The positions of the T, I, and P axes are denoted and the two solid lines are the planes perpendicular to the T and P axis. The areas where compressional waves leaving the source have a first motion in the away direction are shown as stippled. For types a and b the points where rays penetrate the focal sphere are also shown

The results listed in Table 4 and displayed in Fig. 13 provide a sample of the variety that is possible in estimating static moment tensors. Type 1 (Fig. 13a) and type 2 (Fig. 13b) are derived from the amplitudes of discrete phases on the seismograms, whereas types 3 and 4 are derived from the dynamic moment tensor that is obtained from analysis of complete seismograms. Type 3 (Fig. 13c) is obtained from a short time interval at the beginning of the dynamic moment tensor while type 4 (Fig. 13d) is obtained from a broad frequency interval of its spectral modulus. Table 4 shows that all four types have the same general pattern in terms of the signs of the moment tensor elements, but the amplitudes of the elements show considerable variation. The first three types are based on the energy that is contained in relatively short intervals of time and have amplitudes that are much less than the fourth, which is based on energy contained in the entire time interval and a fairly broad frequency range. In spite of these differences, the plots of principal axes shown in Fig. 13 are very similar for the four different types of static moment tensors.

On the basis of the experience acquired in estimating the four different types of static moment tensors of Table 4 and Fig. 13 for all of the events listed in Table 1, some conclusions on the relative reliability of the different types are possible. In general the results for the 20 events are comparable to those listed in Table 4 for event 12, but the plots of the principal axes are not always as consistent as those in Fig. 13. The method of the second type using the amplitudes of p and s waves measured on the seismogram is the least reliable of the four, primarily because of difficulty in accurately measuring the amplitudes of direct shear waves. The method of the third type using the amplitudes of the dynamic moment tensor averaged over a time interval has the disadvantage that the results can depend upon the selected time interval, which makes the results somewhat subjective. The method of the first type using the amplitudes of direct compressional waves measured on the seismogram generally gives results similar to the fourth type, but has the disadvantage of depending on only a few data and is, thus, sensitive to measurement errors. This first type also produces a scalar moment that is considerably smaller than that obtained with spectral methods. On the basis of this experience, the method of the fourth type using the low frequency level of the dynamic moment rate tensor emerges as the most reliable and the preferred method. It is based on a broad range of frequencies and is derived from the analysis of complete three component seismograms. The relative uncertainties for this approach are also the smallest and most consistent.

The uncertainties in estimates of the static moment tensor given in Tables 2 and 4 can be propagated to the eigenvalues and eigenvectors using first-order perturbation analysis (Franklin 1968). When this type of analysis is applied to the estimates of $\tilde{m}_{ij}$ and its uncertainties given in Table 2 for event 12, the results of Table 5 are obtained. Given the results of Table 5, it is straightforward to further propagate the uncertainties to the scalar moment m _o  = 4,779.5 ± 482.6 GNm and the moment magnitude M _w = 2.45 ± 0.04. Thus, the combination of Tables 2, 3 and 5 gives a fairly complete description of estimates with standard errors for the static moment tensor, associated parameters, and basic properties of the source time function for one particular event. Although there are some fluctuations, the uncertainty in the source parameters of this event can be roughly characterized by a coefficient of variation of about 0.4.

Table 5 Estimates of static moment tensor eigenvalues and eigenvectors for event 12

7 General Results

The preceding two sections, Figs. 7 through 13, and Table 2 through 5 outline the procedures used in estimating moment tensors for one event, event 12 of Table 1. Identical procedures are applied to the 19 other events in Table 1, and the results are similar to those already described for event 12. With estimates available for all of the events listed in Table 1, it is possible to examine the similarities and differences of these 20 events that cover a range in location, size, and water injection rate. All of the static moment tensors used in this section are estimated from the low frequency level of the dynamic moment tensor (type 4 of Table 4).

Some additional information about the events selected for moment tensor inversion is listed in Table 6. The events are selected so that the origin times of the events spans the entire time interval from 212 days before until 267 days after the start of injection into P32. The rate of injection at the time of the event is listed in Table 6, as well the horizontal distance of the hypocenter from the well P32. The number of components used in the inversion K is always at least 30. The stability of the dynamic moment tensor inversion is measured by the condition number of the matrix $\mathcal{G}(f)$ (Eq. 4), which is approximated by the ratio of the maximum to minimum eigenvalues (Franklin 1968). This condition number is evaluated at each frequency, with the minimum and maximum values for the entire frequency range listed in Table 6. The maximum values are always at frequencies <1 Hz or >100 Hz, with the maximum values in the intervening interval are never >10.

Table 6 Information about events and dynamic moment tensor inversion

A property of interest about the moment tensors is the relative size of the isotropic part of the moment tensor, as this provides a measure of the volume change in the source region. A discussion of the isotropic part of the moment tensor must include the possibility that it is an artifact, because it appears to be the most poorly resolved part of the moment tensor. Discussions of this matter can be found in O’Connell and Johnson (1988), Vasco and Johnson (1989), Kuge and Lay (1994), Šilený et al. (1996), (2009), Dufumier and Rivera (1997), Julian et al. (1998) and Covellone and Savage (2012). This possibility of a greater uncertainty in the isotropic part is supported by the results listed in Table 7, where $\tilde{m}_{\rm {{iso}}}$ is considerably smaller than m _o , but ${\rm {sd}}[\tilde{m}_{\rm {{iso}}}]$ is only slightly smaller than sd[m _o ]. This means that the relative error in $\tilde{m}_{iso}$ is larger than that in m _o . Expressing this quantitively, the mean coefficient of variation cv[m _o ] as calculated from Table 7 is 0.11, while $cv[\tilde{m}_{\rm {{iso}}}]$ is 0.25, which says that the relative uncertainty of the isotropic part is over twice that of the scalar moment. All of this uncertainty is propagated throughout Table 7 so that meaningful comparisons can be made. Note that O’Connell and Johnson (1988) performed synthetic tests designed to estimate the effect of source mislocation and incorrect velocity model on estimates of the isotropic part of the moment tensor for earthquakes at The Geysers. They found maximum fractional effects in the range of 0.07–0.14 that are entirely consistent with the estimates of ${\rm {sd}}[\tilde{m}_{\rm {{iso}}}/m_o]$ listed in Table 7.

Table 7 Comparison of scalar moment and isotropic moment

With these caveats in mind, consider the comparison of the isotropic part of the moment tensor to the scalar moment in Table 7. The ratio of these two quantities $\tilde{m}_{iso}/m_o$ ranges between −0.21 and +0.47, with the isotropic part negative for 4 and positive for 16 of the events. The mean value of this ratio for all of the events is

$$ \frac{\tilde{m}_{{\rm {iso}}}}{m_o} = 0.19 \pm 0.10. $$

(15)

For the four events with a negative isotropic part, this ratio has a mean of $\tilde{m}_{{\rm {iso}}}/m_o = -0.14$ and an average coefficient of variation of $cv[\tilde{m}_{{\rm {iso}}}/m_o] = 0.87,$ while for the 16 events with positive isotropic part these numbers are $\tilde{m}_{{\rm {iso}}}/m_o = 0.21$ and $cv[\tilde{m}_{{\rm {iso}}}/m_o] = 0.54.$ When individual events are considered, this ratio is close to its uncertainty for some of the events. If one accepts a coefficient of variation <1 as being significant, there are three events with negative isotropic parts and 16 with positive isotropic parts. If one accepts a coefficient of variation <0.5 as being significant, there are no events with negative isotropic parts and nine with positive isotropic parts, leaving 11 events to be classified as not having a significant isotropic part.

The isotropic part of the moment tensor is related to volume change in the source region by the formula

$$ \Updelta V = \frac{\tilde{m}_{{\rm {iso}}}}{\kappa}, $$

(16)

where κ is the elastic bulk modulus. For the event with the largest relative isotropic part, event 7, with elastic parameters from Fig. 6 at the source depth, the volume change is 6.45   m³. Considering all of the earthquakes shown in Fig. 2 in the 300 days after the start of injection, about 90 % of them have hypocenters within a volume of about 2.7 × 10⁹   m³ centered near the bottom of P32. The cumulative scalar moment of the events in this volume is 246 × 10³ GNm and this gives a cumulative isotropic part of 46.1 × 10³ GNm if Eq. 15 is taken as a valid average for all of these events. Then Eq. 16 gives 1.2 × 10³   m³ as an estimate of the cumulative volume change associated with earthquakes near P32, and this is over six orders of magnitude smaller than the volume containing the earthquakes. From Fig. 2, the cumulative volume of water injected into P32 in this same 300 days is 1.4 × 10⁶   m³, and the volume change associated with earthquakes is about three orders of magnitude smaller than this number. Thus, although the presence of an isotropic part in the moment tensors of the induced earthquakes near P32 implies a cumulative increase in volume of over 10³   m³, this amount is insignificant compared to the volume containing the earthquakes or the volume of water injected.

In Tables 2 and 3 it is shown that for event 12 the corner frequencies and high frequency powers of the moment rate spectral moduli are different for the deviatoric and isotropic parts. That same pattern is also present in the other 19 events in Table 1. In Table 8 the average corner frequency of the six devatoric elements of the moment tensor $\overline{f}_{\rm {{cd}}}'$ along with its uncertainty ${\rm {sd}}[\overline{f}_{\rm {{cd}}}']$ is listed and compared with the corner frequency of the isotropic moment tensor f _ci. The data are plotted in Fig. 14. Both corner frequencies exhibit a tendency to decrease with increasing scalar moment, although the scatter is considerable. Linear regression yields

$$ {\rm {log}}_{10}[\overline{f}_{\rm {{cd}}}'] = (1.35 \pm 0.08 ) - ( 0.10 \pm 0.03) \log_{10}[m_o] $$

(17)

for the average corner frequency of the deviatoric moment tensor and

$$ {\rm {log}}_{10}[f_{\rm {{ci}}}] = (1.47 \pm 0.08 ) - ( 0.08 \pm 0.03) \log_{10}[m_o] $$

(18)

for the corner frequency of the isotropic part, with both of these regression lines shown in Fig. 14. These results indicate that, aside from the fact that the isotropic corner frequency is somewhat larger, the two corner frequencies have a similar dependence upon scalar moment. The ratio of the two corner frequencies can also be considered. The dependence on scalar moment is similar for the two so linear regression yields

$$ \frac{f_{\rm {{ci}}}}{\overline{f}_{\rm {{cd}}}'} = 1.46 \pm 0.23. $$

(19)

This result gives a quantitative measure of the difference in corner frequencies between the isotropic and deviatoric parts of the moment tensor.

Table 8 Spectral parameters of dynamic moment tensors

Fig. 14

The corner frequency of the isotropic part of the dynamic moment rate tensor f _ci (open circles and solid line) and the average corner frequency of the deviatoric dynamic moment rate tensor $\overline{f}_{\rm {{cd}}}$ (asterisks and dashed line) as a function of the scalar moment m _o on a log–log plot

The same type of analysis can be performed for the power of the high frequency asymptote. The results are

$$ {\rm {log}}_{10}[\overline{s}_{\rm {{hd}}}'] = (0.36 \pm 0.05 ) + ( 0.04 \pm 0.02) \log_{10}[m_o] $$

(20)

for the average high frequency slope of the deviatoric moment tensor and

$$ {\rm {log}}_{10}[s_{\rm {{hi}}}] = (0.48 \pm 0.05 ) + ( 0.03 \pm 0.02) \log_{10}[m_o] $$

(21)

for the high frequency slope of the isotropic part. There is a slight tendency for the powers to increase as the scalar moment increases. For the ratio of the two powers

$$ \frac{s_{\rm {{hi}}}}{\overline{s}_{\rm {{hd}}}'} = 1.23 \pm 0.09. $$

(22)

The power of the high frequency asymptote for the isotropic part of the moment tensor is clearly larger than that of the deviatoric moment tensor.

Figure 13 shows how stereographic projections can be used to display the principal axes and isotropic fraction of a static moment tensor. In Fig. 15 results of this type are plotted next to the locations of the epicenters for all of the events in Table 1. Some spatial patterns are evident in this figure. A group of eight events to the south of P32 (events 1, 3−7, 12, 18) all have a positive isotropic part and similar orientations of the principal axes, the only varying property being the value of the isotropic fraction. The four events with negative isotropic parts (events 2, 9, 10, 15) all are located north of P32. Events 8 and 13 have near-by hypocenters and have similar mechanisms, whereas event 18 is also nearby but has a quite different mechanism. Event 7 has a mechanism similar to event 18 and a similar epicenter, but has a depth that is about 800 m above the other three events. Events 11, 14, 17, and 20, which form a cluster of events about 400 m east of the bottom of P32, have very similar mechanisms, but event 19 is about 200 m below this cluster and has a completely different mechanism.

Fig. 15

Map showing epicenters of events in Table 1 with attached equal area stereographic projections for static moment tensors

Another way of comparing the principal axes that are plotted in Fig. 15 is to plot them all together, and this is done in Fig. 16 for the T and P axis. The T axes are all close to horizontal with nine of the events tightly clustered in the northwest-southeast direction. These nine events (1, 3–7, 12, 17, 18) all have positive isotropic parts (Table 7) and have an average azimuth of N48°W. This common orientation of this group of events is clearly displayed in Fig. 15 where it is also seen that all in the group, except event 17, are located south of P32. The P axes range from horizontal to near vertical, which indicates both dip-slip mechanisms (P axis near vertical) and strike-slip mechanisms (P axis near horizontal).

Fig. 16

Equal area stereographic projections of the a T axes and b P axes on the lower half of the focal sphere for the 20 events in Table 1

8 Discussion and Conclusions

A general objective of this study is to investigate source mechanisms of earthquakes at The Geysers by solving for their first-degree dynamic moment tensors. The results are first obtained in the frequency domain, but are easily transformed to the time domain. The major difficulty of this approach, as is the case in many inverse problems, is to assess the uncertainty of the dynamic moment tensors. There are two primary sources of this uncertainty, the uncertainty in the observational data and inaccuracies in the Green functions that describe the wave propagation effects. The limitations of the experimental protocol, such as the instrument response or the distribution of recording stations, are treated as part of the uncertainty in the data.

The manner in which uncertainty in the observational data and Green functions gets transformed into uncertainty in the dynamic moment tensors is best considered in the frequency domain. There it is found that the uncertainty is sufficiently large to prevent a confident interpretation of the moment tensors for frequencies <1 Hz and for frequencies >100 Hz. In both cases there is a small signal-to-noise ratio caused by a weak signal that is due to a fall-off in the instrument response at low frequencies and a fall-off in the source spectrum at high frequencies. The conclusion is that the dynamic moment tensors of this study are only reliable for frequencies between 1 and 100 Hz. Within this frequency interval, based on the degree of fit between the observed and calculated spectral moduli, it is concluded that the spectral moduli of the dynamic moment tensors are estimated with an uncertainty of about 10–50 %. However, based on the lack of fit between the observed and calculated time functions, it is concluded that most of the uncertainty of the dynamic moment tensors resides in the spectral phases. While some of the features of the dynamic moment rate functions in the time domain appear to be real, the reliability of other features cannot be established.

Even when restricted to the use of the spectral moduli in a limited frequency range, the estimation of dynamic moment tensors is still an effective method of investigating seismic source mechanisms. This approach has the advantage that it is based on essentially all of the information contained on the seismograms and does not require any subjective identifications and measurements of specific seismic phases. The spectral moduli of the dynamic moment tensors are easily parameterized in a manner that provides quantitative information about the source mechanism. Of the different types of static moment tensors investigated in this study, it is concluded that the most reliable is based on the low frequency level of spectral moduli from dynamic moment rate functions. The corner frequency of the source time function and the power of its high-frequency asymptote can also be determined with this approach.

Many of the results obtained in this study are consistent with those of other studies. Kirkpatrick et al. (1996), Ross et al. (1996, 1999) and Guilhem et al. (2014) all found about half of the events at The Geysers to have significant isotropic parts, both positive and negative, with the fraction as large as 0.3. The results listed in Table 7 are generally consistent with these other studies, with the isotropic fraction as large as 0.47 in one case. However, when uncertainties are also considered, conclusions about the fraction of events with significant isotropic parts and the existence of events with negative isotropic parts depend upon the level of significance that is desired. Both Oppenheimer (1986) and Kirkpatrick et al. (1996) found the T axis of focal mechanisms to be predominantly horizontal, and this agrees with Fig. 16a.

The parameterized spectral modulus of the dynamic moment tensor provides useful information about the corner frequency and the power of the high frequency asymptote of the source time functions. The results of this study suggest that there can be significant differences between these parameters for the isotropic part and the deviatoric moment tensor. The finding that the average corner frequency of the isotropic part is more than 40 % larger than that of the deviatoric moment tensor is a significant difference. An explanation could simply be that the isotropic part is primarily determined by p waves, while the deviatoric moment tensor is primarily determined by s waves. Sato and Hirasawa (1973) developed a kinematic failure model of a circular shear crack and found that the ratio of the corner frequency of radiated p waves to radiated s waves varied between 1.26 and 1.39 as the rupture velocity varied between 0.5 and 0.9 times the shear velocity at the source.

The estimated corner frequencies are also affected by the models of attenuation used in the moment tensor inversion, and this could play a role in determining the ratio of the isotropic to deviatoric corner frequencies. A series of tests were performed for six of the events listed in Table 1 (1, 7, 9, 12, 14, and 19) in order to explore this possibility. First, the Q _p values of the velocity model were increased by a factor of two to Q _p  = 200 above sea level and Q _p  = 400 below sea level and the entire inversion process repeated. The primary effect of this change is to increase the power of the high frequency asymptote for the isotropic part so that there is a slight increase in the corner frequencies of both the isotropic and deviatoric parts of the dynamic moment tensor with little change in their ratio. Next, the Q _s values of the velocity model were decreased by a factor of two to Q _s  = 50 above sea level and Q _s  = 100 below sea level and the entire inversion process repeated once again. The change in this case causes an increase in the corner frequency $\overline{f}_{\rm {{cd}}}'$ of the deviatoric part, but there is also an increase in the corner frequency of the isotropic part f _ci. The net result is a ratio of the isotropic to deviatoric corner frequencies that is reduced to near 1.0 for four of the events (1, 7, 9, and 14) but remains at approximately 1.4 for the other two events (12 and 19). Thus, the cause of the observed difference between the isotropic and deviatoric corner frequencies remains uncertain, with possible explanations including a natural effect of the source failure process, an incorrect treatment of attenuation, or it could be that the isotropic and deviatoric parts are produced by two different source processes.

The focal mechanisms shown in Figs. 15 and 16 contain two somewhat contradictory features. Groups of events contained in a certain spatial area have very similar focal mechanisms, both with respect to the orientation of the principal axes, and the sign of the isotropic part. At the same time, close to some of the members of such a group there are other events that have completely different focal mechanisms. Further investigation is needed to determine if these spatial patterns are related to features of the geology or hydrology.

A matter not yet discussed is the correlation between the water injection rate and the properties of the earthquakes selected for moment tensor inversion (Fig. 2). The reason for this is that no specific correlation has been detected. There appear to be no recognizable differences between the moment tensors of earthquakes that occurred before injection began and those that occurred after injection began, nor do the moment tensors appear to change as the rate of injection changes. These facts suggest that earthquakes occur whenever water is added at the appropriate depth, with both the number and largest size of the earthquakes being related to the amount of added water. The small number of earthquakes that occurred before the beginning of injection into P32 can be explained as due to natural recharge from rain and streams and possibly from wells more distant than P32. This type of reasoning is similar to that of Majer and Peterson (2007) where the matter is discussed in more detail.

The careful examination of a large number of seismograms recorded at The Geysers supports the idea that scattering of elastic waves plays an important role in determining the appearance of these seismograms. For instance, the observed seismograms in Fig. 7 show many of the features considered by Sato et al. (2012) as indicative of high frequency scattering by correlated random heterogeneity, including the codas of P and S waves that last longer than the expected source duration, an S coda that is more prominent than that of P, and a tendency for equipartition of motion on the different components. The fact that the seismograms at each station have certain distinctive characteristics, such as frequency content, shape of phase arrivals, and duration of phases, that are independent of the source suggests that much of this scattering is taking place near the seismic station. This idea is consistent with the problems encountered in estimating dynamic moment tensors because scattering will have a minor effect upon the modulus of the Fourier transform of the seismogram but will have a major and largely random effect upon the phase. It helps explain why amplitudes of static moment tensors based on individual phases are significantly smaller than those based on the spectral modulus of the dynamic moment rate tensor (Table 4). Patton and Aki (1979) discuss this matter of how various types of noise can cause fluctuations in the spectral amplitudes and incoherency in the spectral phases of the moment tensor.

Reasons for scattering of high frequency elastic waves at The Geysers can be found in the topography and heterogeneity in material properties. Numerical simulations have shown that topography such as that found at The Geysers can cause variations in the amplitudes of seismic waves of more than 50 % at frequencies above 2 Hz (Boore 1972, 1973; Bouchon et al. 1996). The effects of heterogeneity in velocity has also been investigated with numerical calculations (Frankel and Clayton 1986; O’Connell 1999; Sato et al. 2012) and effects similar to those shown in Fig. 7 can be produced by velocity variations of only about 5 %. The effects of heterogeneity are complicated and involve the types of correlation functions used to describe the velocity variations, the variance and correlation length of velocity variations, the relative roles of forward and backward scattering, and whether the scattering is single or multiple. The properties of the attenuation that accompanies the scattering are particularly sensitive to these details of the scattering process. These results suggest that understanding the cause of uncertainty in the moment tensor estimates may require a thorough characterization of scattering in the shallow crust at The Geysers, a fairly difficult task that is beyond the scope of the present study.

If scattering plays the significant role that is suggested, then some of the inaccuracy in the Green functions may be related to the manner in which attenuation is included, as the phase responses of intrinsic attenuation and scattering attenuation are generally different. Uncertainty in the type and values of attenuation included in the Green functions will also have an effect upon the corner frequencies and high frequency powers that are listed in Table 8. Three-dimensional variations in the attenuation may also be important. Romero et al. (1997) found that frequency dependent attenuation corrections had to be made for each recording site at The Geysers.

The testing and validation of the results of this study will require comparisons with data from other disciplines such as geology and hydrology. Given that injection of water causes an increase in the number of earthquakes (Fig. 2), the presence and pressure of liquids and gases plus changes in temperature may all play a role in the earthquake process. Further effort is also required to help establish that moment tensor results obtained in this study of 20 events are truly representative of the over 2,000 other events that occurred in the same study area in the same time interval. Finally, a better understanding of the results could benefit from the development of a physical model of the earthquake source process that is appropriate for these types of induced earthquakes, and that is the subject of a companion study (Johnson 2014).