Abstract
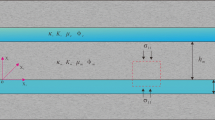
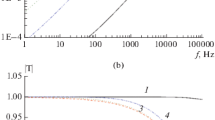
Wave-induced fluid flow generates a dominant attenuation mechanism in porous media. It consists of energy loss due to P-wave conversion to Biot (diffusive) modes at mesoscopic-scale inhomogeneities. Fractured poroelastic media show significant attenuation and velocity dispersion due to this mechanism. The theory has first been developed for the symmetry axis of the equivalent transversely isotropic (TI) medium corresponding to a poroelastic medium containing planar fractures. In this work, we consider the theory for all propagation angles by obtaining the five complex and frequency-dependent stiffnesses of the equivalent TI medium as a function of frequency. We assume that the flow direction is perpendicular to the layering plane and is independent of the loading direction. As a consequence, the behaviour of the medium can be described by a single relaxation function. We first consider the limiting case of an open (highly permeable) fracture of negligible thickness. We then compute the associated wave velocities and quality factors as a function of the propagation direction (phase and ray angles) and frequency. The location of the relaxation peak depends on the distance between fractures (the mesoscopic distance), viscosity, permeability and fractures compliances. The flow induced by wave propagation affects the quasi-shear (qS) wave with levels of attenuation similar to those of the quasi-compressional (qP) wave. On the other hand, a general fracture can be modeled as a sequence of poroelastic layers, where one of the layers is very thin. Modeling fractures of different thickness filled with CO2 embedded in a background medium saturated with a stiffer fluid also shows considerable attenuation and velocity dispersion. If the fracture and background frames are the same, the equivalent medium is isotropic, but strong wave anisotropy occurs in the case of a frameless and highly permeable fracture material, for instance a suspension of solid particles in the fluid.










Similar content being viewed by others
References
Bakulin A., Grechka V., Tsvankin I. (2000) Estimation of fracture parameters from reflection seismic data—Part I: HTI model due to a single fracture set. Geophysics 65:1788–1802
Brajanovski M., Gurevich B., Schoenberg M. (2005) A model for P-wave attenuation and dispersion in a porous medium permeated by aligned fractures. Geophysical Journal International 163:372–384
Carcione J.M. (1996) Wave propagation in anisotropic, saturated porous media: plane wave theory and numerical simulation. Journal of the Acoustical Society of America 99:2655–2666
Carcione, J. M. (2007) Wave fields in real media: Wave propagation in anisotropic, anelastic, porous and electromagnetic media, Handbook of Geophysical Exploration, vol. 38, Elsevier (2nd edition, revised and extended).
Carcione, J. M., Gei, D., Picotti, S., and Michelini, A. (2012), Cross-hole electromagnetic and seismic modeling for CO2 detection and monitoring in a saline aquifer, Journal of Petroleum Science and Engineering 100:162–172, doi:10.1016/j.petrol.2012.03.018. http://dx.doi.org/10.1016/j.petrol.2012.03.018
Carcione J.M., Gurevich B., Cavallini F. (2000) A generalized Biot-Gassmann model for the acoustic properties of shaley sandstones. Geophys. Prosp 48:539–557
Carcione J.M., Picotti S. (2006) P-Wave seismic attenuation by slow-wave diffusion: Effects of inhomogeneous rock properties. Geophysics 71:O1–O8
Carcione J.M., Santos J.E., Picotti S. (2011) Anisotropic poroelasticity and wave-induced fluid flow. Harmonic finite-element simulations. Geophysical Journal International 186:1245–1254
Carcione, J. M., Santos, J. E., and Picotti, S. (2012), Fracture-induced anisotropic attenuation, Rock Mech. Rock Eng, doi:10.1007/s00603-012-0237-y.
Chapman M. (2003) Frequency dependent anisotropy due to meso-scale fractures in the presence of equant porosity. Geophysical Prospecting 51:369–379
Chichinina T.I., Obolentseva I.R., Ronquillo-Jarillo G. (2009) Anisotropy of seismic attenuation in fractured media: Theory and ultrasonic experiment. Transport in Porous Media 79:1–14
Du Q.Z., Wang X.M., Ba J., Zhang Q. (2011) An equivalent medium model for wave simulation in fractured porous rocks. Geophysical Prospecting, doi:10.1111/j.1365-2478.2011.01027.x
Gelinsky S., Shapiro S.A. (1997) Poroelastic backus-averaging for anisotropic, layered fluid and gas saturated sediments. Geophysics 62:1867–1878
Galvin R.J., Gurevich B. (2009) Effective properties of a poroelastic medium containing a distribution of aligned cracks. Journal of Geophysical Research 114:B07305 doi:10.1029/2008JB006032.
Gurevich B. (2003) Elastic properties of saturated porous rocks with aligned fractures. Journal of Applied Geophysics 54:203–218
Gurevich B., Brajanovski M., Galvin R.J., Müller T. M., Toms-Stewart J. (2009) P-wave dispersion and attenuation in fractured and porous reservoirs–poroelasticity approach. Geophysical Prospecting 57:225–237
Hsu C.J., Schoenberg M. (1993) Elastic waves through a simulated fractured medium. Geophysics 58:964–977
Krief M., Garat J., Stellingwerff J., Ventre J. (1990) A petrophysical interpretation using the velocities of P and S waves (full waveform sonic). The log Analyst 31:355–369
Krzikalla, F., and Müller, T. (2011), Anisotropic P-SV-wave dispersion and attenuation due to inter-layer flow in thinly layered porous rocks, Geophysics, 76, WA135; http://dx.doi.org/10.1190/1.3555077.
Lambert, G., Gurevich, B., and Brajanovski, M. (2005), Frequency-dependent anisotropy of porous rocks with aligned fractures, Poromechanics III, Proceedings of 3rd Biot Conference on Poromechanics, May 2005, pp. 309–314.
Lambert G., Gurevich B., Brajanovski M. (2006) Attenuation and dispersion of P-waves in porous rocks with planar fractures: Comparison of theory and numerical simulations. Geophysics 71:N41–N45
Mavko, G., Mukerji, T., and Dvorkin, J. (2004), The Rock Physics Handbook, Cambridge University Press.
Müller T., Gurevich B., Lebedev M. (2010) Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks—a review. Geophysics 75:A147–A164
Norris A.N. (1993) Low-frequency dispersion and attenuation in partially saturated rocks. J. Acoust. Soc. Am 94:359–370
Picotti, S., Carcione, J. M., Gei, D., Rossi, G., and Santos, J. E. (2012), Seismic modeling to monitor CO2 geological storage: The Atzbach-Schwanenstadt gas field, J. Geophys. Res., 117, B06103, 18 PP., doi:10.1029/2011JB008540.
Pride S.R., Berryman J.G., Harris J.M. (2004) Seismic attenuation due to wave-induced flow. J. Geophys. Res 109:B01201 doi:10.1029/2003JB002639.
White J.E., Mikhaylova N.G., Lyakhovitskiy F.M. (1975) Low-frequency seismic waves in fluid saturated layered rocks. Izvestija Academy of Sciences USSR, Phys. Solid Earth 11:654–659
Acknowledgments
J.E.S was partially funded by PIP 112-200801–00952 (CONICET, Argentina). J.M.C and S.P. have been partially funded by the European Union under the framework of the CO2CARE project. We thank two anonymous reviewers for useful comments.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix
Wave Velocities and Quality Factors
The complex velocities are required to calculate wave velocities and quality factors of the fractured medium. They are given by
(Carcione, 2007), where \(l_1 = \sin \theta\) and \(l_3 = \cos \theta\) are the directions cosines, θ is the propagation angle between the wavenumber vector and the symmetry axis, and the three velocities correspond to the qP, qS and SH waves, respectively. The phase velocity is given by
where v represents either v qP, v qSV or v SH. The energy–velocity vector of the qP and qSV waves is given by
(Carcione, 2007), where
defines the angle between the energy–velocity vector and the z-axis (the ray angle),
where the upper and lower signs correspond to the qP and qSV waves, respectively. Moreover,
(Carcione, 2007), where “pv” denotes the principal value, which has to chosen according to established criteria.
On the other hand, the energy velocity of the SH wave is
Finally, the quality factor is given by
Rights and permissions
About this article
Cite this article
Carcione, J.M., Gurevich, B., Santos, J.E. et al. Angular and Frequency-Dependent Wave Velocity and Attenuation in Fractured Porous Media. Pure Appl. Geophys. 170, 1673–1683 (2013). https://doi.org/10.1007/s00024-012-0636-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-012-0636-8