Skip to main content
SpringerLink
Log in

Simplicial complexes with rigid depth

  • Published:
Archiv der Mathematik Aims and scope Submit manuscript

Abstract

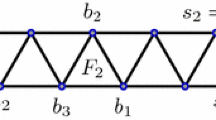
We extend a result of Minh and Trung (Adv. Math. 226:1285–1306, 2011) to get criteria for depth \({I = \rm {depth}\sqrt{I}}\) , where I is an unmixed monomial ideal of the polynomial ring S = K[x 1, . . . , x n ]. As an application we characterize all the pure simplicial complexes Δ which have rigid depth, that is, which satisfy the condition that for every unmixed monomial ideal \({I\subset S}\) with \({\sqrt{I}=I_\Delta}\) one has depth(I) = depth(I Δ).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. W. Bruns and J. Herzog, Cohen-Macaulay rings, Revised Ed., Cambridge University Press, 1998.

  2. J. Herzog and T. Hibi, Monomial ideals, Graduate Texts in Mathematics 260, Springer, 2010.

  3. J. Herzog, D. Popescu, and M. Vlădoiu, Stanley depth and size of a monomial ideal, to appear in Proceed. AMS.

  4. J. Herzog A., Soleyman Jahan., Zheng X.: Skeletons of monomial ideals. Math.Nachr. 283, 1403–1408 (2010)

    Article  MathSciNet  Google Scholar 

  5. Herzog J., Takayama Y., Terai N.: On the radical of a monomial ideal, Arch. Math. 85, 397–408 (2005)

    MathSciNet  MATH  Google Scholar 

  6. Hibi T.: Quotient algebras of Stanley-Reisner rings and local cohomology. J. Algebra. 140, 336–343 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  7. E. Miller, B. Sturmfels Combinatorial commutative algebra, Graduate Texts in Mathematics 227, Springer, 2005.

  8. Minh N.C., Trung N.V.: Cohen-Macaulayness of monomial ideals and symbolic powers of Stanley-Reisner ideals. Adv. Math. 226, 1285–1306 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Takayama Y.: Combinatorial characterizations of generalized Cohen-Macaulay monomial ideals, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 48, 327–344 (2005)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Abdus Salam School of Mathematical Sciences (ASSMS), GC University, Lahore, Pakistan

    Adnan Aslam

  2. Faculty of Mathematics and Computer Science, Ovidius University, Bd. Mamaia 124, 900527, Constanta, Romania

    Viviana Ene

  3. Institute of Mathematics of the Romanian Academy, P.O. Box 1-764, 014700, Bucharest, Romania

    Viviana Ene

Authors
  1. Adnan Aslam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Viviana Ene
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Viviana Ene.

Additional information

Viviana Ene was supported by the grant UEFISCDI, PN-II-ID-PCE- 2011-3-1023.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Aslam, A., Ene, V. Simplicial complexes with rigid depth. Arch. Math. 99, 315–325 (2012). https://doi.org/10.1007/s00013-012-0421-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00013-012-0421-z

Mathematics Subject Classification (2010)

Keywords

Search

Navigation