Skip to main content
SpringerLink
Log in

Propagation of singularities and maximal functions in the plane

  • Published:
Inventiones mathematicae Aims and scope

Summary

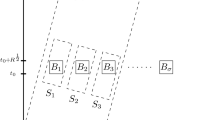
In this work we mainly generalize Bourgain's circular maximal function to include variable coefficient averages. Our techniques involve a combination of Bourgain's basic ideas plus microlocal analysis. In particular, to see the role of curvature, we rely heavily on methods used in studying propogation of singularities for hyperbolic differential equations. We also show that, forp>2, there is local smoothing inL p for solutions to the wave equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Besse, A.L.: Manifolds all of whose geodesics are closed. Berlin Heidelberg New York: Springer 1978

    Book  MATH  Google Scholar 

  2. Bourgain, J.: Averages in the plane over convex curves and maximal operators. J. Analyse Math.47, 69–85 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  3. Carbery, A.: The boundedness of the maximal Bochner-Riesz operator onL 4(ℝ2). Duke Math. J.50, 409–416 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Carleson, L., Sjölin, P.: Oscillatory integrals and a multiplier problem for the disk. Studia Math.44, 287–299 (1972)

    MathSciNet  MATH  Google Scholar 

  5. Constantin, P., Saut, J.: Local smoothing properties of dispersive equations. J. Amer. Math. Soc.1, 431–439 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  6. Falconer, K.J.: The geometry of fractal sets. Cambridge: Cambridge Univ. Pres 1985

    Book  MATH  Google Scholar 

  7. Hörmander, L.: Fourier integrals I. Acta Math.127, 79–183 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hörmander, L.: The spectral function of an elliptic operator. Acta Math.88, 341–370 (1968)

    MathSciNet  MATH  Google Scholar 

  9. Hörmander, L.: The analysis of linear partial differential operators III, IV. Berlin Heidelberg New York: Springer 1985

    MATH  Google Scholar 

  10. Journé, J.-L., Soffer, A., Sogge, C.D.: Decay estimates for Schrödinger operators. Comm. Pure Appl. Math. (to appear)

  11. Kaneko, M., Sunouchi, G.: On the Littlewood-Paley and Marcinkiewicz functions in higher dimensions. Tôhoku Math. J.37, 343–365 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  12. Kato, T.: On the Cauchy problem for the (generalized) Kortveg-de Vries equation. In: Studies in Applied Math., pp. 9–23, Academic Press 1986

  13. Peral, J.:L p estimates for the wave equation. J. Funct. Anal.36, 114–145 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  14. Phong, D.H., Stein, E.M.: Hilbert integrals, singular integrals and Radon transforms I. Acta Math.157, 99–157 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  15. Seeger, A., Sogge, C.D., Stein, E.M.: Regularity properties of Fourier integral operators, Ann. Math. (to appear)

  16. Sjölin, P.: Regularity of solutions to the Schrödinger equation. Duke Math. J.55, 699–715 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  17. Sogge, C.D., Stein, E.M.: Averages over hypersufaces: smoothness of generalized Radon transforms. J. Anal. Math.54, 165–188 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  18. Stein, E.M.: Singular integrals and differentiability properties of functions. Princeton: Princeton Univ. Press 1970

    MATH  Google Scholar 

  19. Stein, E.M.: Maximal functions: spherical means. Proc. Nat. Acad. Sci.73, 2174–2175 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  20. Stein, E.M.: Oscillatory integrals in Fourier analysis. In: Beijing lectures in harmonic analysis, pp. 307–356. Princeton: Princeton Univ. Press 1986

    Google Scholar 

  21. Stein, E.M., Wainger, S.: Problems in harmonic analysis related to curvature. Bull. Amer. Math. Soc.84, 1239–1295 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  22. Stein, E.M., Weiss, G.: Introduction to Fourier analysis on Euclidean spaces. Princeton: Princeton Univ. Press 1971

    MATH  Google Scholar 

  23. Vega, L.: Schrödinger equations: pointwise convergence to the initial data. Proc. Amer. Math. Soc.102, 874–878 (1988)

    MathSciNet  MATH  Google Scholar 

  24. Wilder, J.B.: The non-Euclidean Kakeya problem. In: Proceedings of the 25th summer meeting of the Canadian Mathematical Congress. 1971, pp. 603–607

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of California, 90024, Los Angeles, CA, USA

    Christopher D. Sogge

Authors
  1. Christopher D. Sogge
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Oblatum 7-IX-1990

The author was supported in part by the NSF.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sogge, C.D. Propagation of singularities and maximal functions in the plane. Invent. math. 104, 349–376 (1991). https://doi.org/10.1007/BF01245080

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01245080

Keywords

Search

Navigation