Skip to main content
SpringerLink
Log in

Chair-Free Berge Graphs Are Perfect

  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

Abstract

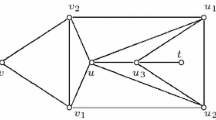
A graph G is called Berge if neither G nor its complement contains a chordless cycle with an odd number of nodes. The famous Berge’s Strong Perfect Graph Conjecture asserts that every Berge graph is perfect. A chair is a graph with nodes {a, b, c, d, e} and edges {ab, bc, cd}, eb. We prove that a Berge graph with no induced chair (chair-free) is perfect or, equivalently, that the Strong Perfect Graph Conjecture is true for chair-free graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Berge, C.: Färbung von Graphen, deren sämlitche bzw, ungerade Kreise starr sind (Zusammenfassung), Wiss, Z. Mar-tin Luther Univ. Halle Wittenberg, Math. Nat. Reihe (1961) 114.

  2. Berge, C., Chvátal, V. Eds.: Topics on Perfect Graphs. Annals of Discrete Mathematics, Vol 21 Amsterdam: North Holland 1984

  3. Conforti, M., Cornuéjols, G., Kapoor, A., Vušković, K.: A Mickey Mouse Decomposition Theorem, Proceedings IPCO IV, Copenhagen, (May 1995)

  4. Chvátal, V.: On certain polytopes associated with graphs. J. Comb. Theory ser. B 18, 138–154 (1975)

    Article  Google Scholar 

  5. Chvátal, V.: Star cutsets and perfect graphs. J. Comb. Theory ser. B 39, 189–299 (1985)

    Article  Google Scholar 

  6. Chvátal, V., Sbihi, N.: Bull-free Berge graphs are perfect. Graphs and Comb. 3, 127–139 (1987)

    Article  MATH  Google Scholar 

  7. De Simone, C., Galluccio, A.: New classes of Berge perfect graphs. Discrete Math. 131, 67–79 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  8. De Simone, C., Sassano, A.: Stability Number of Bull and Chair Free Graphs. Discrete Appl. Math. 41, 121–129 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  9. Galluccio, A., Sassano, A.: The rank facets of the stable set polytope for claw-free graphs. Technical Report n. 340, IASI-CNR, Rome (1994) J. Comb. Theory ser. B (1997) (to be published)

  10. Lovász, L.: Normal Hypergraphs and the perfect graph conjecture. Discrete Math. 2, 253–267 (1972)

    Article  MATH  MathSciNet  Google Scholar 

  11. Lovász, L.: A Characterization of Perfect Graphs, J. Comb. Theory ser. B 13, 95–98 (1972)

    Article  Google Scholar 

  12. Lovász, L., Plummer, M.: Matching Theory. Annals of Discrete Mathematics, Vol 29 Amsterdam: North Holland 1986

    Google Scholar 

  13. Mannino, C., Sassano, A.: Edge Projection and the Maximum Cardinality Stable Set Problem. In: D.S. Johnson, M.A. Trick: Cliques, Coloring, and Satisfiability: Second DIMACS Implementation Challenge. DIMACS Series in Discrete Mathematics and Theoretical Computer Science (to be published)

  14. Olariu, S.: On the strong perfect graph conjecture. J. Graph Theory 12, 169–176 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  15. Olariu, S.: Paw-free graphs. Information Processing Letters 28, 53–54 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  16. Olariu, S.: The Strong Perfect Graph Conjecture for Pan-free graphs, J. Comb. Theory ser. B 47, 187–191 (1989)

    Article  MathSciNet  Google Scholar 

  17. Padberg, M.W.: Perfect zero-one Matrices. Mathematical Programming, 6, 180–196 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  18. Parthasarathy, K.R., Ravindra, G.: The strong perfect graph conjecture is true for (K 1, 3)-free graphs. J. Comb. Theory ser. B 21 212–223 (1976)

    Article  MathSciNet  Google Scholar 

  19. Parthasarathy, K.R., Ravindra, G.: The validity of the strong perfect graph conjecture for (K 4 − e)-free graphs. J. Comb. Theory ser. B 26, 98–100 (1979)

    Article  MathSciNet  Google Scholar 

  20. Sassano, A.: Reducible cliques and the Strong Perfect Graph Conjecture, IASI Technical Report R.257, (March 1989)

  21. Sebő, A.: On critical edges in minimal imperfect graphs. Proceedings IPCO III, Erice (May 1993).

  22. Seinsche, D.: On a property of the class of n-colorable graphs. J. Comb. Theory ser. B 16, 191–193 (1974)

    Article  MathSciNet  Google Scholar 

  23. Sun, Liping: Two classes of perfect graphs. J. Comb. Theory ser. B 53, 273–292 (1991)

    Article  Google Scholar 

  24. Tucker, A.: Coloring perfect (K 4 − e)-free graphs. J. Comb. Theory ser. B 42, 313–318 (1987).

    Article  Google Scholar 

  25. Tucker, A.: Critical perfect graphs and perfect 3-chromatic graphs. J. Comb. Theory ser. B 23, 143–149 (1977)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Informatica e Sistemistica, Università di Roma “La Sapienza”, via Buonarroti, 12 - 00185, Roma, Italy

    Antonio Sassano

Authors
  1. Antonio Sassano
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antonio Sassano.

Additional information

This work was partially supported by MURST, Roma, Italy and Progetto Finalizzato Trasporti II, CNR, Italy

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sassano, A. Chair-Free Berge Graphs Are Perfect. Graphs and Combinatorics 13, 369–395 (1997). https://doi.org/10.1007/BF03353015

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03353015

Keywords

Search

Navigation