Attractors and confiners in demography

Abstract

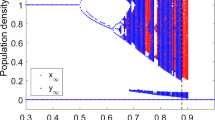
Various dynamical models have been suggested by demographers to understand or to better forecast fertility fluctuations. Usual linear techniques have proved poor, but nonlinear techniques may help us to find out some temporal qualitative structure, and to take into account breakdown phenomena. For instance, the 1931–1985 fluctuations may be better described by drawing first return functions, which show a precise qualitative behaviour: two attractors exchanging the trajectory in the phase space under the perturbing environment of the historical context. A second example is drawn from a 17th century population, at a time when people were submitted to high and very irregular mortality. Because of the stochastic nature of the process, attractors are difficult to determine, and we resort to tools which are different from usual asymptotic attractors. These tools, called confiners, are the stochastic analogue of the notion of attractor for stochastic dynamical processes. They have been defined by Cosnard and Demongeot on the basis of the set of accumulation points of the trajectory, and rely on the essential intuitive property of invariance through the double operation consisting first in searching the confining basin of a set, then in taking the limit of this basin. The notion of confiner enables a rigourous description of the equilibrium states of the process: For fertility fluctuations during the 17th century, it reveals two confining zones exchanging the trajectory. Moreover, a simulation system shows how the existence of these two zones are directly linked to the frequencyv of mortality crisis occurring, that is to say, according to the valuev, the population dynamics will more or less balance towards a resistance to the crisis or towards a usual renewal of the population.