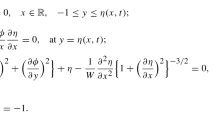Summary
Considered here are model equations for weakly nonlinear and dispersive long waves, which feature general forms of dispersion and pure power nonlinearity. Two variants of such equations are introduced, one of Korteweg-de Vries type and one of regularized long-wave type. It is proven that solutions of the pure initial-value problem for these two types of model equations are the same, to within the order of accuracy attributable to either, on the long time scale during which nonlinear and dispersive effects may accumulate to make an order-one relative difference to the wave profiles.
Similar content being viewed by others
References
Abdelouhab, L., Bona, J. L., Felland, M., & Saut, J.-C. (1989) Non-local models for nonlinear dispersive waves.Physica D 40, 360–392.
Arnold, D. N. & Winther, R. (1982) A superconvergent finite element method for the Korteweg-de Vries equation.Math. Comp. 38, 23–36.
Baker, G. A., Dougalis, V. A., & Karakashian, O. A. (1983) Convergence of Galerkin approximations for the Korteweg-de Vries equation,Math. Comp. 40, 419–433.
Benjamin, T. B. (1967) Internal waves of permanent form in fluids of great depth.J. Fluid Mech. 29, 559–592.
Benjamin, T. B., Bona, J. L., & Mahony, J. J. (1972) Model equations for long waves in nonlinear dispersive systems.Phil. Trans. Royal Soc. London A 272, 47–78.
Bona, J. L. & Bryant, P. J. (1973) A mathematical model for long waves generated by wavemakers in nonlinear dispersive systems.Proc. Cambridge Phil. Soc. 73, 391–405.
Bona, J. L. & Dougalis, V. A. (1980) An initial- and boundary-value problem for a model equation for propagation of long waves.J. Math. Anal. Applic. 75, 503–522.
Bona, J. L., Dougalis, V. A., & Karakashian, O. A. (1986) Fully discrete Galerkin methods for the Korteweg-de Vries equation.Comp. & Maths, with Appls. 12A, 859–884.
Bona, J. L., Dougalis, V. A., Karakashian, O. A., & McKinney, W. R. (1990) Fully discrete methods with grid refinement for the generalized Korteweg-de Vries equation. To appear inProceedings of the Conference on Viscous Profiles and Numerical Methods for Shock Waves.
Bona, J. L., Dougalis, V. A., Karakashian, O. A., & McKinney, W. R. (1991) Conservative, high-order schemes for the generalized Korteweg-de Vries equation. To appear.
Bona, J. L., Pritchard, W. G., & Scott, L. R. (1981) An evaluation of a model equation for water waves.Phil. Trans. Royal Soc. London A 302, 457–510.
Bona, J. L., Pritchard, W. G., & Scott, L. R. (1983) A comparison of solutions of two model equations for long waves. In the proceedings of the AMS-SIAM conference on fluid dynamical problems in astrophysics and geophysics, Chicago, July 1981Lectures in Applied Mathematics,20 (N. Lebovitz, ed.), American Math. Soc., Providence RI, pp. 235–267.
Bona, J. L. & Saut, J.-C. (1991) Dispersive blow-up of solutions of generalized Korteweg- de Vries equations. To appear inJ. Diff'l Eqns.
Bona, J. L. & Winther, R. (1983) The Korteweg-de Vries equation, posed in a quarter plane.SIAM J. Math. Anal. 14, 1056–1106.
Bona, J. L. & Winther, R. (1989) The Korteweg-de Vries equation in a quarter plane, continuous dependence results.Diff'l & Integral Eqns. 2, 228–250.
Brezis, H. & Wainger, S. (1980) A note on limiting cases of Sobolev embeddings and convolution inequalities.Commun, in PDE 5 773–789.
Dougalis, V. A. & Karakashian, O. A. (1985) On some high order accurate fully discrete Galerkin methods for the Korteweg-de Vries equation.Math. Comp. 45, 329–345.
Felland, M. (1991) Decay and smoothing of solutions of nonlinear wave equations with dissipation and dispersion. Ph.D. thesis, University of Chicago.
Hammack, J. L. (1973) A note on tsunamis: their generation and propagation in an ocean of uniform depth.J. Fluid Mech. 60, 769–799.
Hammack, J. L. & Segur, H. (1974) The Korteweg-de Vries equation and water waves. Part 2. Comparison with experiments.J. Fluid Mech. 65, 289–314.
Hormander, L. (1976)Linear partial differential operators. Springer-Verlag, Berlin.
Kruskal, M. (1975) Nonlinear wave equations, theory and applications. In Dynamical Systems, Theory and Applications. (J. Moser, ed.)Lecture Notes in Physics 38, Springer-Verlag, New York-Heidelberg, 310–354.
Kubota, T., Ko, D., & Dobbs, L. (1978) Weakly-nonlinear long internal gravity waves in stratified fluids of finite depth.J. Hydrodynamics 12, 157–165.
Newell, A. C. (editor) (1974) Nonlinear wave motion.Lectures in Applied Mathematics 15, American Math. Soc., Providence, RI.
Peregrine, D. H. (1966) Calculation of the development of an undular bore.J. Fluid Mech. 25, 321–330.
Saut, J.-C. (1979) Sur quelques généralisations de l'équation de Korteweg-de Vries.J. Math. Pures Appliq. 58, 21–61.
Stoker, J. J. (1957)Water waves. Wiley-Interscience, New York.
Winther, R. (1980) A conservative finite element method for the Kortweg-de Vries equation.Math. Comp. 34, 23–43.
Zabusky, N. J. & Galvin, C. J. (1971) Shallow-water waves, the Korteweg-de Vries equation and solitons.J. Fluid Mech. 47, 811–824.
Author information
Authors and Affiliations
Additional information
Communicated by Thanasis Fokas
This research was supported in part by the National Science Foundation. A considerable portion of the project was completed while the first author was resident at the Institute for Mathematics and Its Applications, University of Minnesota.
Rights and permissions
About this article
Cite this article
Albert, J.P., Bona, J.L. Comparisons between model equations for long waves. J Nonlinear Sci 1, 345–374 (1991). https://doi.org/10.1007/BF01238818
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01238818