Skip to main content
Springer Nature Link
Log in

Design of multi-component structural systems for optimal layout topology and joint locations

  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

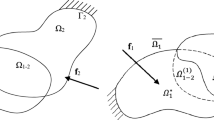
Present day topology optimization techniques for continuum structures consider the design of single structural components, while most real life engineering design problems involve multiple components or structures. It is therefore necessary to have a methodology that can address the design of multi-component systems and generate designs for the optimal layouts of individual structures and locations for interconnections. The interconnections include supports provided by the ground, joints and rigid connections like rivets, bolts and welds between components. While topology optimization of structures has been extensively researched, relatively little work has been done on optimizing the locations of the interconnections. In this research, a method to model and define domains for the interconnections has been developed. The optimization process redistributes material in the component design domains and locates the connections optimally based on an energy criterion. Some practical design examples are used to illustrate the capability of this method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Maxwell, J. (1872) On reciprocal figures, frames, and diagrams of force. Transactions of the Royal Society, Edinburgh, 26, 1

    Google Scholar 

  2. Michell, A. (1904) The limits of economy of material in frame-structure. Phil. Mag, 8, 589–597

    Google Scholar 

  3. Schmit, L. (1960) Structural design of systematic synthesis. In Proceedings of the 2nd ASCE Conf Electr Comp, Pittsburgh, PA, 105–122

  4. Haftka, R.; Grandhi, R. (1986) Structural shape optimization-a survey. Computer Methods in Applied Mechanics and Engineering, 57, 91–106

    Google Scholar 

  5. Bendsøe, M.; Kikuchi, N. (1988) Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 71, 197–224.

    Google Scholar 

  6. Rozvany, G.; Bendsóe, M.; Kirsch, U. (1995) Layout optimization of structures. Applied Mechanics Review, 48, 2, 41–119

    Google Scholar 

  7. Chirehdast, M.; Gea, H. C.; Kikuchi, N.; Papalambos, P. (1994) Structural configuration examples of an integrated optimal design process. Journal of Mechanical Design, 116, 997–1004

    Google Scholar 

  8. Menassa, R.; DeVries, W. (1991) Optimization methods applied to selecting support positions in fixture design. Journal of Engineering for Industry, 113, 412–418

    Google Scholar 

  9. Yoshimura, M.; Nose, K. (1994) Generation of conceptual design for structural shapes and functional elements of machine systems having no preconceptions concerning the design. Advances in Design Automation, 2, 83–89

    Google Scholar 

  10. Johanson, R.; Papalambros, P.; Kikuchi, N. (1994) Simultaneous topology and material microstructure design. In Advances in Structural Optimization. Proceedings of the Second World Congress on Computational Structures Technology, Athens

    Google Scholar 

  11. Chickermane, H.; Gea, H. C. (1995) Topology optimization of mechanical repairs for aging aircraft. In Computational Mechanics '95, vol. 2, 2171–2176, Springer, Berlin; Proceedings of the International Conference on Computational Engineering Science, July 30–Aug 3, 1995, Hawaii

    Google Scholar 

  12. Gea, H. C. (1996) Topology optimization: a new microstructure based design domain method. Computers and Structures, 61, 4, 781–788

    Google Scholar 

  13. Weng, G. (1984) Some elastic properties of reinforced solids, with special reference to isotropic ones containing isotropic inclusions. International Journal of Engineering Science, 22, 845–856

    Google Scholar 

  14. Mori, T.; Tanaka, K. (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. ACTA Metallurgica, 21, 571–574

    Google Scholar 

  15. Eshelby, J. (1957) The determination of the elastic field of an ellipsoidal inclusion and related problems. Proceedings of the Royal Society, A241, 379–396

    Google Scholar 

  16. Chickermane, H.; Gea, H. (1996) A new local function approximation method for structural optimization problems. International Journal of Numerical Methods in Engineering, 39, 829–846

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, Rutgers, The State University of New Jersey, 08855-0909, Piscataway, NJ, USA

    H. Chickermane & H. C. Gea

Authors
  1. H. Chickermane
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. H. C. Gea
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chickermane, H., Gea, H.C. Design of multi-component structural systems for optimal layout topology and joint locations. Engineering with Computers 13, 235–243 (1997). https://doi.org/10.1007/BF01200050

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01200050

Keywords